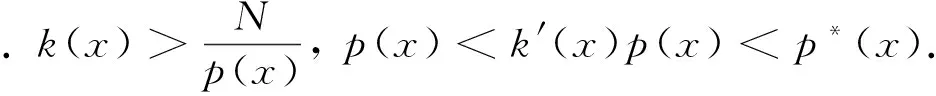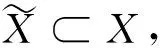带类p(x)-拉普拉斯算子的问题在全空间上的多重解①

唐映， 储昌木

贵州民族大学 数据科学与信息工程学院， 贵阳 550025

考虑如下带类p(x)-拉普拉斯算子的椭圆方程：

(1)

近年来， 包含p(x)-拉普拉斯算子的椭圆方程及变分方法的研究， 受到了学者们的广泛关注(见文献[1-14])． 涉及变指数的数学模型可用于描述弹性力学和电流变液等物理现象． 文献[6]研究了如下椭圆方程的特征值问题：

(2)

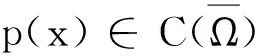
(AR) 存在M>0，θ>p+， 使得

0<θF(x，t)≤tf(x，t) |t|≥M，x∈Ω

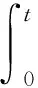
当f(x，u)满足(AR)条件和一些附加条件时， 文献[6]证明了： 任意的λ>0均为方程(2)的一个特征值．

最近， 文献[15]在λ=1的情形下考虑了方程(2)解的存在性和多重性， 当f(x，u)满足超线性增长条件但不满足(AR)条件时， 利用山路引理获得了方程(2)非平凡解的存在性． 然而， 当Ω=RN时， 对该类椭圆方程的研究不多． 本文将研究f(x，u)满足超线性增长条件但不满足(AR)条件(见文献[16])时， 方程(1)非平凡解的存在性．

我们给出如下假设条件：

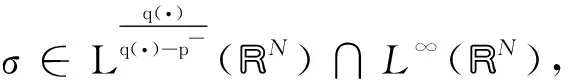
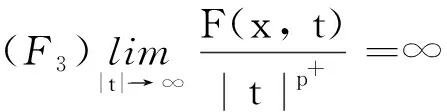
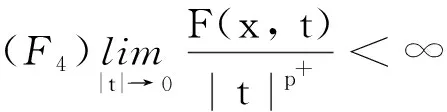
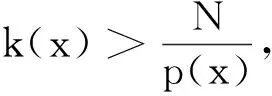
|F(x，t)|k(x)≤c0|t|k(x)p(x)F(x，t)

(F6)f(x， -t)=-f(x，t)对所有x∈RN和t∈R成立．

本文的主要结果如下：

定理1假设条件(V)，(H)和(F1)-(F6)成立， 则方程(1)有无穷多解．

记ζ(RN)是由所有可测实函数组成的集合． 变指数Lebesgue空间

对应的范数为

变指数Sobolev空间

W1，p(·)(RN)={u∈Lp(·)(RN)： |u|∈p(x)(RN)}

对应的范数为

‖u‖W1，p(·)(RN)=‖u‖Lp(·)(RN)+‖u‖Lp(·)(RN)

定义

其对应的范数为

当V满足条件(V)时， 容易验证范数‖u‖X与‖u‖1，p(x)等价[16]．

命题1[2]对所有的u∈Lp(·)(RN)，v∈Lp′(·)(RN)， 有

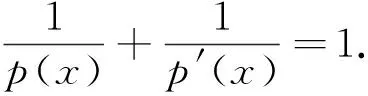
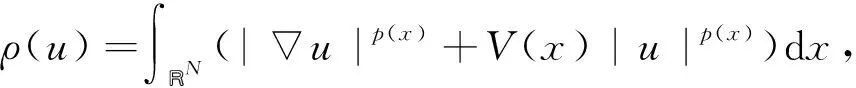
(i)ρ(u)>1(=1； <1)⟺‖u‖X>1(=1； <1)；

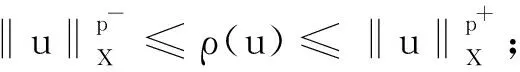
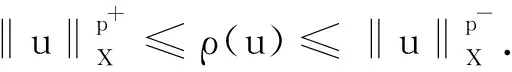
定义泛函

则φ(u)∈C1(X，R)且

定义

则ψ(u)∈C1(X， R)， 且

类似文献[6，16]的证明， 有如下命题成立：

(i) 若条件(V)成立， 则XLp(·)(RN)是紧嵌入；

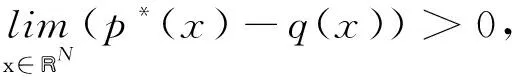
定义1若对所有的v∈X， 有

则称u∈X是方程(1)的弱解．

方程(1)对应的能量泛函为

众所周知， 方程(1)的弱解与泛函I的临界点等价．

引理1[17]设E是无限维Banach空间，E=Y⨁Z， 其中Y为有限维空间． 若对于任意c都有J∈C1(E， R)满足(Ce)c条件，J(0)=0，J(-u)=J(u)， 且

(i) 存在常数ρ0，α>0， 使得J|∂Bρ0∩Z≥α；

则J有一列临界值趋于∞的序列．

令{ei}为X上的标准正交基， 且定义Ei=span{ei}． 记

则

E=span{ei：i∈N}=Yk⨁Zk

由引理2， 我们可以选择一个正整数m≥1， 使得

(3)

设

E=XY=YmZ=Zm

则X=Y⨁Z．

引理3如果条件(V)，(H)，(F1)-(F5)成立， 则泛函I满足(Ce)c条件．

证设{un}是I在X中的(Ce)c序列， 即

(4)

若ω≠0， 设

Ω1={x∈RN：ω(x)≠0}

(5)

因此， 由(4)，(5)式及Fatou引理， 有

(6)

矛盾．

p(x)≤s(x)

当n充分大时， 有

(7)

设

Ωn(a，b)={x∈RN：a≤|un(x)|

(8)

由(8)式可知

(9)

(10)

(11)

与(9)式矛盾．

因此

(12)

则

结合(12)式， 有

(13)

由文献[1]可知存在著名的Simon不等式， 即对所有的ξ，η∈RN，C是只依赖p-，p+的常数，

Δ1={x∈RN：p(x)≥2}Δ2={x∈RN： 1

满足

(14)

(15)

(16)

(17)

存在L>0， 有

(18)

引理4假设定理1中的条件都成立， 则存在常数ρ0，α>0， 使得I|∂Bρ0∩Z≥α．

证由命题5可知存在常数C3>0， 使得

|u|Lq(x)(RN)≤C3‖u‖X

(19)

由条件(F2)，(F4)， 存在C1>0，C4>0， 有

|F(x，t)|≤C1|t|p++C4|t|q(x)∀(x，t)∈(RN， R)

(20)

对于u∈Zm， 由(3)，(19)和(20)式可得

取‖u‖X=ρ0， 由p+

定理1的证明由引理3可知， 泛函I满足(Ce)c条件． 由引理4和引理5可知， 泛函I满足引理1的所有假设． 故定理1得证．