椭圆球面波信号Wigner-Ville分布显式渐近求解方法

王红星 赵乐源* 陆发平 刘传辉 康家方

①(海军航空大学 烟台 264001)

②(山东省信号与信息处理重点实验室 烟台 264001)

③(中国人民解放军 91206部队 青岛 266000)

1 引言

椭圆球面波函数(Prolate Spheroidal Wave Functions, PSWFs)作为一类特殊的非正弦函数，具有双完备正交、时域波形严格奇偶对称、时间带宽积与频谱灵活可控、能量聚集性最佳的带限函数集等优良特性[1,2]。基于PSWFs信号的非正弦波通信可直接在时频域2维空间进行信号波形设计，具有信号波形设计灵活性、高能量聚集性以及高频谱效率等诸多优良特性，非常符合新一代通信系统的信号波形设计需求，是一种极具有应用潜力和推广前景的通信新体制[3—5]。

在利用PSWFs信号进行信息加载、检测、滤波等信号处理的过程中，都会涉及PSWFs信号基础特性的运用[6]。其中，时频分布特性反映PSWFs信号频率随时间变化情况以及时频能量分布情况，对于PSWFs信号的检测具有重要意义。传统的PSWFs信号的检测，大都沿用基于正交性的相关检测[7,8]，在信道条件恶劣、正交性被破坏时，检测效果较差。而根据PSWFs信号时频分布特性，从时频域上提取有用PSWFs信号时频特征参量用以检测，有望突破正交性的束缚，提升检测性能。

为进一步挖掘PSWFs信号的时频特性，文献[9]引入Wigner-Ville分布(Wigner-Ville Distribution, WVD)，分析了PSWFs信号WVD交叉项的时频分布规律；文献[10]引入平滑Wigner-Ville分布(Smoothed Wigner-Ville Distribution, SWVD)，分析了交叉项抑制情况下的PSWFs信号时频分布；文献[11]引入短时傅里叶变换(Short Time Fourier Transform, STFT)、S变换(Stockwell Transform, ST)等时频分析工具，分析了线性时频分析方法下的PSWFs信号的时频特性。研究发现，相对于STFT, S变换等时频分析方法，WVD的时频分辨率更高，且不受窗函数的影响，能够为PSWFs信号时频检测提供更为精确的时频特征参量[12]。此外，WVD能够反映信号间相互作用的规律，已广泛应用于一些重要信号的检测[13,14]。

然而，由于PSWFs信号无闭式解析解，无法直接根据显式闭式表达式分析其时频特性。前期关于PSWFs信号时频特性的研究都是采用数值仿真分析方法进行的，求得的PSWFs信号时频分布结果存在误差且误差不可控，PSWFs信号原有的奇偶对称性在时频分布结果中已经不再保持。数值仿真处理使得信号全部采样点都参与运算，导致后续信号处理复杂度较高，而信号时频分布的对称性将在降低信号处理复杂度方面发挥重要的作用[15]。若能产生一种误差可控的PSWFs信号WVD显式渐近表达式，且能保持信号原有的对称特性，根据表达式进行时频特性定量分析甚至时频检测，将会是一个更为有效的办法。目前对于PSWFs信号时频显式渐近表达式及其求解方法的研究，尚未见国内外相关文献报道。

Legendre多项式作为一种完备的正交多项式，在时域上线性叠加可逼近PSWFs信号[16]；其具有天然的奇偶对称性，且线性运算后对称性保持不变，使得逼近的PSWFs信号将保持严格奇偶对称。基于上述思路，本文将Legendre多项式与WVD相结合，提出一种PSWFs信号WVD显式渐近求解方法。本方法能够根据误差要求，生成所需阶数的Legendre多项式WVD自项、交叉项，进而与对应的WVD-Legendre系数相乘后线性叠加，获取PSWFs信号WVD显式渐近表达式。理论与数值仿真结果表明，所提方法产生的渐近表达式能够满足误差要求，实现误差可控，且能够有效保持信号原有的对称性。此外，在相同采样点数情况下，相对于PSWFs信号数值解的WVD，所提方法得到的PSWFs信号WVD频域分辨率更高，为根据显式渐近表达式进行时频特性定量分析甚至时频检测提供了有效途径。

2 PSWFs信号WVD显式渐近表达式的导出

为导出PSWFs信号WVD显式渐近表达式，下面将Legendre多项式和WVD相结合，具体为将基于Legendre多项式的PSWFs信号显式表达式与PSWFs信号WVD表达式相结合，并简要分析表达式积分限。

文献[18]对PSWFs函数的Legendre多项式表达给出了详细的理论证明，基于Legendre多项式的PSWFs信号显式表示为

式(5)即为基于Legendre多项式的PSWFs信号的WVD显式表达式。

在实际应用中，式(5)归一化Legendre多项式的自项、交叉项阶数无法取到无穷，需要控制渐近阶数K，求解一定误差ε下的PSWFs信号WVD显式渐近表达式。因此，PSWFs信号在渐近阶数为K时，WVD显式渐近表达式可表示为

3 WVD-Legendre系数与渐近阶数的求解

3.1 WVD-Legendre系数求解

PSWFs信号与Legendre多项式都具有严格奇偶对称性，其奇偶对称性与阶数有关[1]。阶数为偶数时，PSWFs信号与Legendre多项式都为偶对称；阶数为奇数时，PSWFs信号与Legendre多项式都为奇对称。由式(8)可知，当Legendre多项式与PSWFs信号奇偶性不同时，两者相乘后为奇函数，经过积分后，Legendre多项式系数为0，故只需求解奇偶性相同的Legendre多项式及其对应系数即可。

对于任1阶Legendre多项式Pk(t)，满足微分方程

3.2 矩阵A阶数及渐近阶数求解

由式(7)可知，所提方法产生的PSWFs信号WVD显式渐近表达式的精度与所需Legendre多项式的渐近阶数K有关，阶数越高，逼近精度越高；同时，还需要求解矩阵A的阶数M。下面通过分析PSWFs信号WVD与Legendre多项式自项、交叉项的相关值，来求解矩阵A的阶数M和渐近阶数K，并给出最终的PSWFs信号WVD渐近表达式。

这一结论对矩阵A阶数M及渐近阶数K的求解具有理论指导作用，不足是该界限对于渐近阶数K而言更为宽泛，进而使渐近表达式求解复杂度增加。

(1)矩阵A阶数求解。根据Moyal’s公式[20]，Legendre多项式的WVD自项与PSWFs信号的WVD自项的内积为

(2)渐近阶数求解。理论上，所需Legendre多项式的WVD自项、WVD交叉项的阶数K应该与矩阵A的阶数M一致，即K=M。在实际工程应用中，为进一步降低空间复杂度，需在误差允许的范围内，减少Legendre多项式的储存阶数。

由此可以得到Legendre多项式的WVD自项、WVD交叉项的渐近阶数K应满足

由式(8)可知，奇偶性不同的PSWFs信号与Legendre多项式互相关值为0，故可对奇、偶阶PSWFs信号WVD渐近表达式分开求解，以降低计算复杂度。此外，为保证Legendre多项式的WVD自项、交叉项与PSWFs信号的WVD互相关值都小于ε2，应满足Legendre多项式大于K。故在渐近阶数为K时，PSWFs信号WVD显式渐近表达式可表示为

4 数值仿真验证

本节结合数值仿真，主要从渐近阶数验证、时域频域对称性、时域频域分辨率3个方面对所提方法进行验证，给出由所提方法得到的PSWFs信号WVD在误差控制、时域波形以及频域波形的对称性、时域频域分辨率等方面，与基于数值解的PSWFs信号WVD[11]的对比分析结果。具体系统参数设置如表1所示，其中，基于数值解的PSWFs信号WVD方法参数设置与本文所提方法参数设置一致。

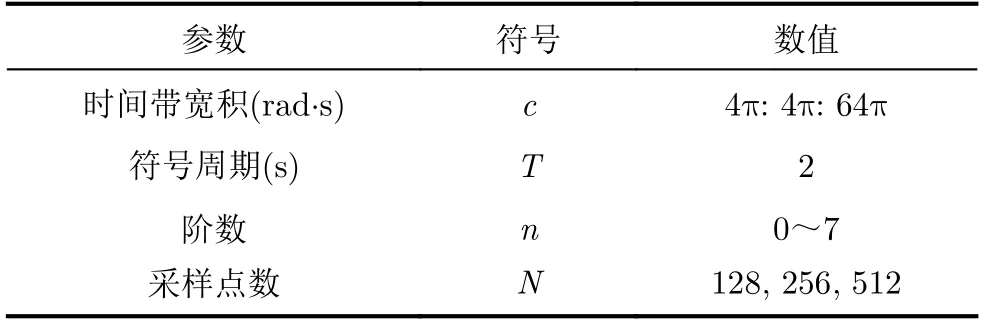
表1 PSWFs信号仿真参数设置

4.1 渐近阶数验证

WVD-Legendre系数能够反映Legendre多项式WVD自项、交叉项与PSWFs信号WVD的相关程度，进而反映Legendre多项式WVD自项、交叉项渐近PSWFs信号WVD的误差大小。下面结合数值仿真，给出不同阶PSWFs信号对应的WVD-Legendre系数，并验证渐近阶数K的有效性。由于Legendre多项式WVD自项与交叉项所需的阶数K是一致的，下面仅分析Legendre多项式WVD自项对应的系数。

时间带宽积为8π rad·s的PSWFs信号对应的WVD-Legendre系数如图2所示。由图2可知，在ε=10—3即ε2=10—6时，渐近阶数K取18；根据本文所提方法可知，此时矩阵A阶数M取149，渐近阶数K=18＜149。而若根据文献[19]，渐近阶数K与矩阵A阶数M都要取149。故在实际求解过程中，文献[19]给出的界限更为宽泛，使得求解复杂度大大增加。

基于数值仿真的方法需要先数值求解产生PSWFs信号，然后经过离散WVD。此过程存在PSWFs信号求解误差与舍入误差。对于PSWFs信号求解误差，参照文献[21]，采用Legendre多项式逼近PSWFs信号的方法。给定误差阈值ε，PSWFs信号求解所需的Legendre多项式阶数为m。然后经过离散WVD，将存在舍入误差，且根据离散WVD基本原理，WVD需要信号自相关后积分，此时的误差将增大且大于ε。

通过上述分析可知，基于数值仿真的PSWFs信号WVD均采用数值解进行处理，存在求解误差、舍入误差，误差计算复杂度高。本文所提方法采用直接控制Legendre多项式WVD逼近PSWFs信号WVD的方式，通过控制渐近阶数实现误差控制。并结合图2表明，本文所提方法求得的渐近表达式既可满足误差要求、实现误差可控，又可有效降低空间复杂度。

4.2 WVD时域、频域对称性

WVD具有时间、频率边缘性，对WVD沿频率轴积分，可得信号瞬时能量分布；对WVD沿时间轴积分，可得信号能量谱密度，故信号时域、频域单一能量域的性能能够直接反映时频域的性能。

对称均方误差(Mean Square Error, MSE)[15]可用来判断信号的对称性，根据文献[15]，MSE值越小，对称性越好。PSWFs信号时域MSE如图3(a)所示。从数值仿真结果可知，基于数值解的PSWFs信号WVD，其时域MSE始终大于0，而本文所提方法产生的WVD时域MSE始终为0。这表明基于数值解的PSWFs信号WVD时域对称性缺失，而本文所提方法能够保持PSWFs信号WVD在时域上严格对称。

PSWFs信号频域MSE如图3(b)所示。从数值仿真结果可知，基于数值解的PSWFs信号WVD，其频域MSE始终大于0，而本文所提方法产生的WVD频域MSE始终为0。这表明基于数值解的PSWFs信号WVD频域对称性缺失，而本文所提方法能够保持PSWFs信号WVD在频域上严格对称。

4.3 WVD时域、频域分辨率

本文所提方法通过对时间、频率等间隔取点，得到PSWFs信号的WVD。基于数值解的PSWFs信号WVD，是PSWFs信号数值解经过离散WVD得到的，整个过程都是离散化处理。其中，基于DPSS的数值解PSWFs信号vn(t)方法，可用于快速产生PSWFs信号数值解，下面将其作为对比对象，其WVD表示为

时间带宽积为4π的0阶PSWFs信号的时频分布如图4所示，其中图4(a)—图4(c)为基于数值解的PSWFs信号WVD图，图4(d)为本文所提方法得到的PSWFs信号WVD图。由数值仿真结果可知：

(1)在信号采样点数一致的情况下，即图4(b)与图4(d)，基于数值解的PSWFs信号WVD时频栅格[17]时间长度为0.008 s，频率长度为0.2 Hz；而本文所提方法得到的PSWFs信号WVD时频栅格时间长度为0.008 s，频率长度为0.025 Hz。这表明在信号采样点数一致的情况下，本文所提方法得到的PSWFs信号WVD和基于数值解的PSWFs信号WVD在时域上具有一样的分辨率，但在频域上本文所提方法分辨率更高。

(2)从图4(a)—图4(c)，采样点数逐渐增加，基于数值解的PSWFs信号WVD时频栅格时间长度逐渐减小，频率长度保持不变。这表明通过增加采样点数，可以提高基于数值解的PSWFs信号WVD时域分辨率，但无法提高频域分辨率，与理论分析一致。

(3)基于数值解的PSWFs信号WVD与本文所提方法得到的PSWFs信号WVD，时频能量密度具有一致的变化趋势。如0阶PSWFs信号，由时频中心到时频区间端点，其时频能量密度逐渐降低。

需要注意的是，由于PSWFs具有高时频能量聚集性，图4只给出了其在有限时频区域内的图像，实际上图4(a)—图4(c)中N×N个采样点所占的时频区域要大于图4(d)给出的时频区域。

通过上述分析可知，所提方法求得的渐近阶数能够始终满足误差要求，验证了本文所提方法的有效性。同时，相对于基于数值解的PSWFs信号WVD，本文所提方法求得的PSWFs信号WVD能够有效保持PSWFs信号原有的时域、频域的对称性，且频域分辨率更高。

5 结束语

原PSWFs信号时频特性分析是以PSWFs数值解为处理对象，无法给出表达式，且误差不可控，难以做深入的定量分析；此外，数值仿真得到的PSWFs信号WVD对称性难以保持。针对上述问题，本文提出一种PSWFs信号WVD显式渐近求解方法，本方法除能够解决上述问题外，还为根据渐近表达式分析PSWFs信号时频特性提供了有效途径。同时，能够为PSWFs信号时频特性的应用奠定理论基础。如根据本文所提方法产生的渐近表达式，通过提取PSWFs信号特定时频区域内的特征参量进行检测，有望实现信噪比的提升，进而提升检测性能；并且，根据渐近表达式的对称性，只取一半信号用于检测，可在检测性能保持不变的前提下大幅降低信号处理复杂度，这也是课题组下一步所要研究的方向。