基于水平集和浸入边界方法的鳗鲡科鱼类游动模拟研究

崔 祚，汪阳生，周后村

（1.贵州理工学院航空航天工程学院，贵阳 550003；2.中国空气动力研究与发展中心，四川 绵阳 621000）

0 引 言

经过亿万年自然进化，鱼类为捕获食饵、逃避敌害和繁殖后代等生存需要，获得了优异的水下运动能力，既可以在持久巡游下保持高效率，也可在逃逸状态下爆发极高的游动加速度，还可在复杂狭小环境中实现高机动性游动[1]。目前，鱼类仿生学研究已经取得了诸多进展，并在生物流体力学以及仿生水下航行器等方面形成特色[2]。虽然研究人员设计了多种仿生水下航行器，但航行器的推进性能远逊色于鱼类的游动性能，其重要原因在于仿生学者并未完全揭示鱼类高效快速游动机理，特别是柔性鱼体与流体之间的相互作用过程[3]。

目前，计算流体力学（Computational Fluid Dynamics，CFD）被广泛应用到鱼类游动的数值模拟中。与实验分析相比，数值模拟方法能够克服实验操作困难和可重复性差等缺点。同时，鱼游数值模拟结果能够提供鱼体周围流场的压力分布、速度分布以及尾迹涡量信息，为定量研究鱼类游动性能和游动机理提供了条件。鱼类游动的数值模拟研究属于典型流固耦合问题，基于数值方法求解Navier-Stokes 方程组，根据鱼体几何形状和运动模型来设定边界条件，计算出流场参数在连续区域上的离散分布，从而获得鱼类游动过程中流场随时间变化的细节信息，有利于揭示鱼类游动机理。例如，Liu等[4]在粘性非定常流条件下，分析了鳗鲡运动模式的游动性能和尾迹流场结构；Carling 和Williams[5]分析了二维鳗鱼自主游动中流体粘性对推进性能的影响；Borazjani 和Sotiropoulos[6-7]研究了鳗鲡模式在粘性流体、过渡区流体和无粘流等情况下的游动性能，并与鲹科模式鱼类对比，探讨了鱼体波参数对鱼类游动速度、游动效率以及流场特征等的影响；Kern 等[8]分析了鳗鲡模式鱼类自主游动过程中推进效率和尾涡控制等流场信息，并提出了优化推进性能的设计方法；Gazzola 等[9]将流固耦合算法与增强学习等优化算法相结合，实现了以提高游动效率为目标的鱼体运动学和形态参数优化。

在自然界，鱼类的游动发生于非定常惯性流体环境中，数值模拟研究存在鱼体外形复杂以及边界运动等难点。目前，新的网格生成方法和流固耦合数值算法为鱼游数值模拟的计算效率和计算精度提供了实现途径。对于复杂的几何边界，贴体网格的生成过程复杂、速度慢。对于动边界问题，贴体网格需借助网格变形和动网格技术，计算量大。鉴于此，本文采用level-set（LS）函数描述复杂的鱼体界面，利用浸入边界法（IB）模拟鱼体与流体之间的相互作用力，即采用IB-LS 数值方法来模拟鱼类游动[10]。该方法通过在控制方程中加入体积力源项来模拟边界对流场的作用，然后在固定直角网格上进行离散求解。该方法前期已被应用到复杂动边界流动的数值模拟中，具有网格生成简单且不需要考虑边界形状的优点。与前期工作[10]相比，本文以鳗鲡科鱼类为研究对象，重点分析鱼类游动性能与鱼体波动曲线参数以及流体环境等因素的复杂关系，其中鱼体波动曲线可通过摆动幅值、摆动频率以及波动曲线波数等参数进行评价。

1 数值方法

1.1 N-S控制方程

对无穷远处的来流速度U∞和特征长度L进行无量纲化，鱼类游动不可压流体的Navier-Stokes 控制方程为

式中：xi(i= 1,2,3 )为以L作无量纲化的三个坐标方向x、y和z；ui为三个坐标方向的速度u、v和w；t为以L/U∞作无量纲化的时间；p为以ρU2∞作无量纲化的压力，ρ为流体密度；Re为流体雷诺数，Re=U∞L/ν；fi为鱼体与流体的相互作用力。

对于低雷诺数流体，利用直接求解方法（DNS）进行鱼游的数值模拟。对于高雷诺数流体，采用大涡模拟方法（LES）进行计算，流动的非定常性主要取决于大尺度漩涡的运动，小尺度的运动被认为是各向同性。在数学上对N-S方程进行某种过滤，只计算大尺度的湍流，将小于过滤尺度的湍流用SGS（Samgorinsky eddy viscosity）模型进行分析[11]。相对于DNS 方法，LES 计算量较小，适合模拟高雷诺数流体环境中鱼类复杂游动。采用LES方法的N-S控制方程为

由于采用浸入边界法来模拟鱼游，计算网格不需要考虑鱼体的几何形状，所以将N-S方程直接在直角网格上进行离散。本文采用正交网格进行空间离散，各变量均分布在交错网格上，速度分量定义在面心上，压力和Level-set 函数值等均定义在体积单元中心上。空间离散方法主要包括二阶精度的中心差分格式和迎风非振荡ENO（essentially non-oscillatory）格式。在鱼体模拟中，在鱼体界面附近使用ENO 格式，计算稳定性较好，但耗散较大；在远离鱼体界面的位置使用中心差分格式，数值耗散小。时间推进采用二阶精度Runge-Kutta 格式(RK2)，由Fractional step 方法和Projection 方法来求解不可压流体的N-S 方程，压力泊松方程通过调用PETS 库进行求解。本文所使用的N-S 求解器是在Linux 系统下使用Fortran 语言进行编写，采用MPI 命令实现程序并行运算，具体详见文献[10]。本文计算所需的硬件设备为国家超级计算长沙中心“天河”计算机，二维和三维的鱼游算例分别采用64 个和256 个CPU进行并行计算。

1.2 基于Level-set方法的鱼体界面描述

参考文献[8]，把鳗鲡科鱼体截面简化为椭圆形，其长轴半径ξw(x)和短轴半径ξh(x)分别为

式中，L为鱼体长度，二维鱼体几何尺寸由函数ξw( )x描述。在浸入边界法中，浸入物体的边界形状和位置通常由一套随体运动的拉格朗日网格来描述，拉格朗日点的坐标是弧长和时间的函数。但对于鱼体的复杂边界，很难直接在边界上划分拉格朗日网格，通常需要借助网格划分软件进行网格划分，该方法计算量大，网格划分也较为复杂。

本文采用Level-set 方法来确定鱼体复杂界面，该方法也被用于描述多相流的界面[12]。设Levelset函数为φ(x,t)，鱼体边界上的函数值φ(x,t)= 0，在鱼体内部（固体域内）任意点的函数值为负数，在流体域中函数值为正数。由于Level-set 函数φ(x,t)为距离函数，所以在计算区域内可通过标记鱼体边界附近网格点到边界距离的正负值来判断边界位置，如判断二维计算域第(i,j)个网格点是否为固体点（或流体点），可根据其距离函数的负值（或正值）进行判断。当网格点(i,j)在流体域内且任意相邻网格点在固体域内，则说明该点为最靠近边界的点，即浸入边界法中的加力点。

对于鳗鲡科鱼类复杂的几何边界，本文采用多段函数来描述鱼体的Level-set函数，以二维鱼体外形为例，定义多项式函数，如式（7）所示，将计算域分为三部分，式中y0为某时刻鱼体的摆动位置。

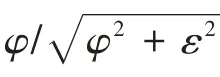
经过20 次重复初始化的迭代，由Level-set 函数描述的鳗鲡科鱼体模型如图1（b）所示，对应的等值线函数间距相等。该结果表明可通过重复初始化方法来修正鱼体界面的Level-set 函数，以满足浸入边界法对鱼体界面描述的要求。

1.3 基于直接力法的浸入边界法

在浸入边界法中，固体边界对流体的作用由体积力场代替，避免了在固体边界上直接施加边界条件，这就使得浸入边界法可以在直角网格上求解流场，而不需要考虑物体边界形状及位置。研究者最初将刚性边界看作具有很大弹性系数的弹性边界，当弹性系数取值较大时，求解力和流场的方程是大刚度系统，需要很小的时间步长实现系统稳定求解；弹性系数取值较小时会导致非物理的弹性作用。这种通过人为指定弹性系数来确定体积力的方法不能适应流场变化，具有局限性[14]。后续Fadlun等[15]根据右端力源项的大小，提出了一种满足边界条件直接确定体积力的方法，即直接力法。在直接力法中，体积力的大小由边界条件决定，并不依赖于具体的流动形式。本文采用基于直接力法的浸入边界法来计算体积力，添加了体积力f后的动量方程为

动量方程的时间离散形式为

其中，RHS（右端项）包含对流项、粘性项以及压力项，即∇·(uu)- ∇p+v∇2u。计算体积力fn+1需要在固体边界上满足速度边界条件，即un+1=Vn+1，即

在式（11）中，边界上的体积力是通过在加力点上施加速度边界条件来实现加力的过程。在计算体积力的过程中，加力点的位置通常不与边界位置重合，所以根据周围固体速度和流体速度共同插值得到加力点速度。本文利用Level-set函数φ( )x,t提供鱼体界面附近直角网格点和边界之间的相对位置信息，并利用φ( )x,t计算界面外法向矢量以及边界附近直角网格点到壁面的距离。其中，鱼体界面任意位置的外法向矢量可表示为= ( ∇φ/| ∇φ|)|φ=0，曲率半径为∇·。

如图2所示，以二维网格为例说明Level-set方法与浸入边界法相结合的过程。首先，通过Level-set 函数找到加力点0，利用Level-set 函数的外法向矢量寻找边界上的固体点1，该点1 与点0 之间的连线垂直于边界。设加力点0的坐标为(x0,y0)，则固体点1的坐标为

式中，nx和ny分别为法向矢量沿x方向和y方向的分量，φ0为加力点0 的Level-set 函数值。然后，寻找加力点0 周边相邻的流体点2 和流体点3，其坐标分别为(x2,y2)和(x3,y3)，则

在接近鱼体边界时，速度场在壁面附近近似满足线性分布，所以近壁流场可通过多项式插值来确定速度分布。本文采用多项式插值的方法来确定加力点速度，即加力点0 的速度由固体点速度1、流体点2和流体点3速度线性插值得到。设插值到加力点0上的速度为u0i(i= 1,2,3 )，则

式中，b1、b2和b3分别为二次线性插值系数，可由固体点速度和流体点速度插值得到：

通过求解系数矩阵A，得到加力点0 上的速度信息(u01,u02,u03)，即加力点0 的速度(u,v,w)，然后根据式(11)求解对应的体积力。此外，由第n步时间推进到第n+1步时，还可以实时监测鱼体的运动速度和位移实现重复迭代，进一步增加数值计算稳定性。

2 鳗鲡科鱼类游动模型

2.1 鱼体自由游动性能评价

在自由游动模型（self-propelled fish model）中，当鱼体从静止开始自由游动时，通过摆动身体产生向前游动的推力，开始初始速度较小，推力大于阻力，鱼体处于加速状态；当鱼体游动速度逐渐增大时，游动阻力也逐渐变大，直到与摆动产生的推力相平衡，达到稳态游动状态。鱼类在自由游动时的控制方程为

式中，Mred为鱼体约化质量。通过沿长度方向线积分求解鳗鲡科鱼体的二维约化质量，为

通过沿长度方向二重积分，求解到鳗鲡科鱼体的三维约化质量为

鱼体在自由游动状态下，达到稳态时所获得的稳态游动速度与流体雷诺数、鱼体波动曲线以及鱼体外形等存在密切关系。所以，在研究鱼体自主游动性能之前，需要明确流体环境、推力以及推进效率等定义：

（1）雷诺数：鱼体自由游动的流体雷诺数定义为L2(Tν)，T为摆动周期；

（2）稳态游动速度：在稳态游动状态下，鱼体对应的游动速度；

（3）平均推力：在稳态游动状态下，鱼体在单位周期内推力的平均值；

（4）游动效率：根据Lighthill细长体理论[16]计算鱼类的游动效率，表达式为

此外，鱼类游动效率也可用Froude效率ηF进行评价，表达式为

2.2 算例设置

Carling和Kern等[5，8]前期研究定义了鳗鲡科鱼类的摆动曲线，表达式为

鳗鲡科鱼体二维算例计算域为50L×4.8L，宽度约为鱼体最大宽度的7 倍，计算域对应网格为2048×256。如图3 所示，在鱼体游动范围内加密网格以保证计算精度，在网格加密区内流向方向网格尺寸Δx为0.02L，侧向方向上的网格尺寸Δy为0.002L。三维鱼游算例计算域为50L×5L×5L，对应网格数为2048×160×160，鱼体周围加密网格尺寸为0.02L×0.005L×0.005L。鱼体位于径向和展向方向中心线上，从起始位置向前游动，流向、径向和展向上边界条件均为无滑移边界条件。

3 鳗鲡科鱼类游动性能分析

3.1 算例验证

参考文献[17-18]，设置鳗鲡科鱼体外形参数和鱼体波曲线分别如式（5）和式（21）所示，流体雷诺数为7100。设置不同的计算网格数以及网格尺寸（见表1），研究网格数对鱼体游动速度的影响。如图4 所示，鱼体由初始静止状态逐渐加速，直到达到稳定游动状态。当网格数为4096×288 时，鱼体稳态速度到达0.55 BL/s（body length/second，体长/秒），与算例IV 中网格数8192×352 的计算结果相一致。与文献网格数对比，本文算例所需网格数约为原网格总数的1/5～1/10，计算量明显减小。

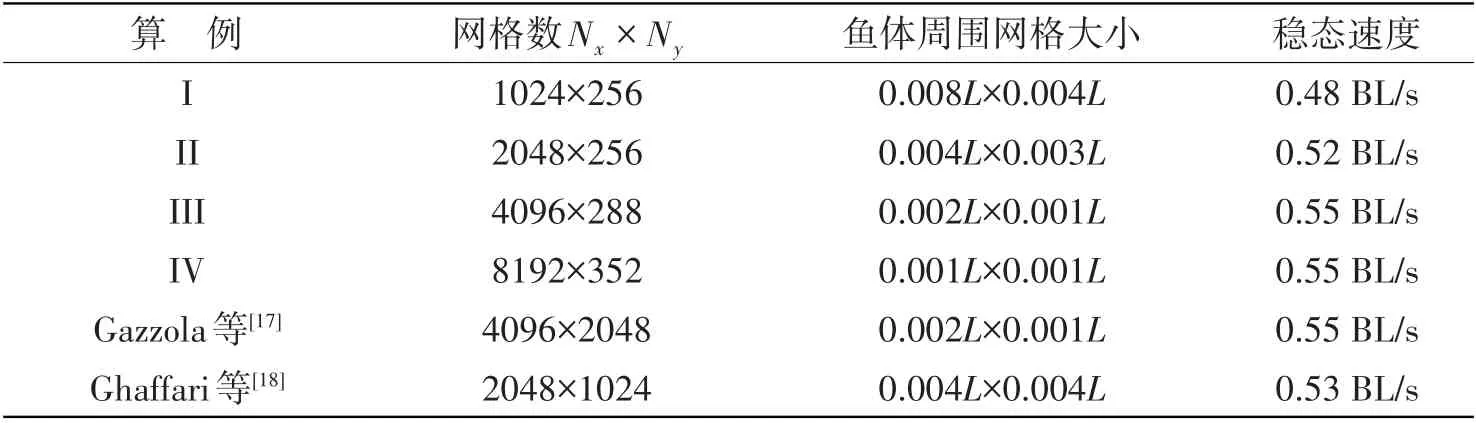
表1 鳗鲡科鱼类自主游动二维算例结果对比Tab.1 Results comparisons of two-dimensional self-propelled anguilliform fish

在稳定游动时，鱼体游动速度会出现往复波动，主要原因在于单位摆动周期内鱼体尾迹会出现两个反向的涡街结构，与尾鳍周期性摆动相对应。如图5（a）所示，二维鱼体在往复摆动过程中会产生不同旋向的附着涡，并在游动过程中沿尾体迅速脱落，在尾迹形成交错排列的反卡门涡街。在反卡门涡之间，尾迹区域会形成一系列连续射流，产生的反作用力会推动鱼体向前游动。在相同的运动学参数下，三维鱼类尾迹出现双列涡和发夹涡等尾涡结构，如图5（b）所示（鱼体尾迹涡街结构的分析见文献[19]）。

3.2 鱼体波参数对推进性能影响分析

在鳗鲡科鱼游模拟中，设置不同粘性的流体以研究鱼类在不同环境中的游动性能。如表2所示，流体雷诺数从500变化到4000，鱼类稳态游动速度从0.14 BL/s增长到0.31 BL/s，游动效率也从60.89%增长到74.12%，而St数从1.23下降到0.55。这说明鱼类在粘度较小的流体中会获得较好的游动性能。在自然界中，鱼类通常在雷诺数Re＞104的流体环境中游动，流体的惯性力起主导作用，而粘性力可忽略不计。鱼类游动对应St数的范围为0.25～0.4，该区间内游动效率最优。在表2 显示的Re=4000 流体环境中，鱼类游动St数达到0.55，该结果说明当前流体的粘性远大于水的粘性。

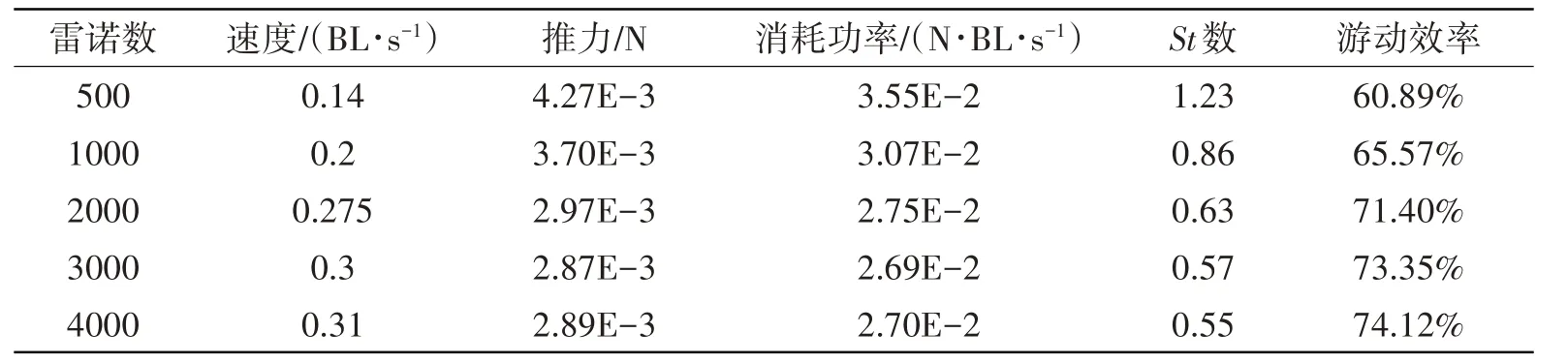
表2 雷诺数对鳗鲡科鱼类游动性能的影响Tab.2 Effects of Reynolds number on swimming performance of anguilliform fish

在不同流体环境中，鱼类的摆动曲线参数会对其推进性能产生较大的影响。以自然界观测的鱼体摆幅为基准成比例改变摆幅，分别选择幅值调节系数为0.25、0.5、1.0、1.5 和2.5，分析不同摆动幅值下鳗鲡科鱼体的游动性能。如表3 所示，当鱼类的摆动幅值调节系数小于1 时，鳗鲡科鱼类的游动速度和推力均随摆动幅值的增大而增大，对应的游动效率也会得到提高。当鱼体摆动幅值调节系数为1.5和2.5时，虽然计算得到较大的游动速度和游动效率，但消耗功率明显增加，不利于提高游动效率。在自然界中，鱼类游动时摆幅基本维持不变[20]，即摆幅调节系数不大于1。该计算结果与自然界中实验观测结论相吻合。

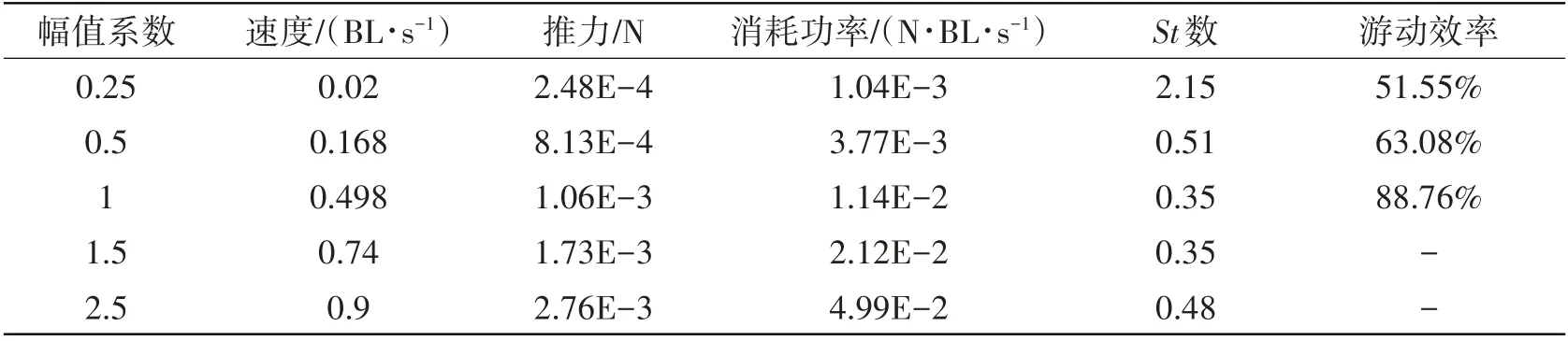
表3 鳗鲡科鱼体摆动幅值系数对游动性能的影响Tab.3 Effects of amplitude coefficient on the swimming performance of anguilliform fish

鱼体摆动曲线波数对游动性能的影响如表4所示。当鱼类摆动曲线波数为9时，鳗鲡科鱼类可获得最大游动速度（0.506 BL/s），游动效率达到最大值89.4%。该结果与鳗鲡科鱼类在自然界进化选择的摆动曲线波数9.75相接近，这也说明本文模型能较好反映鱼类摆动曲线对游动性能的影响。

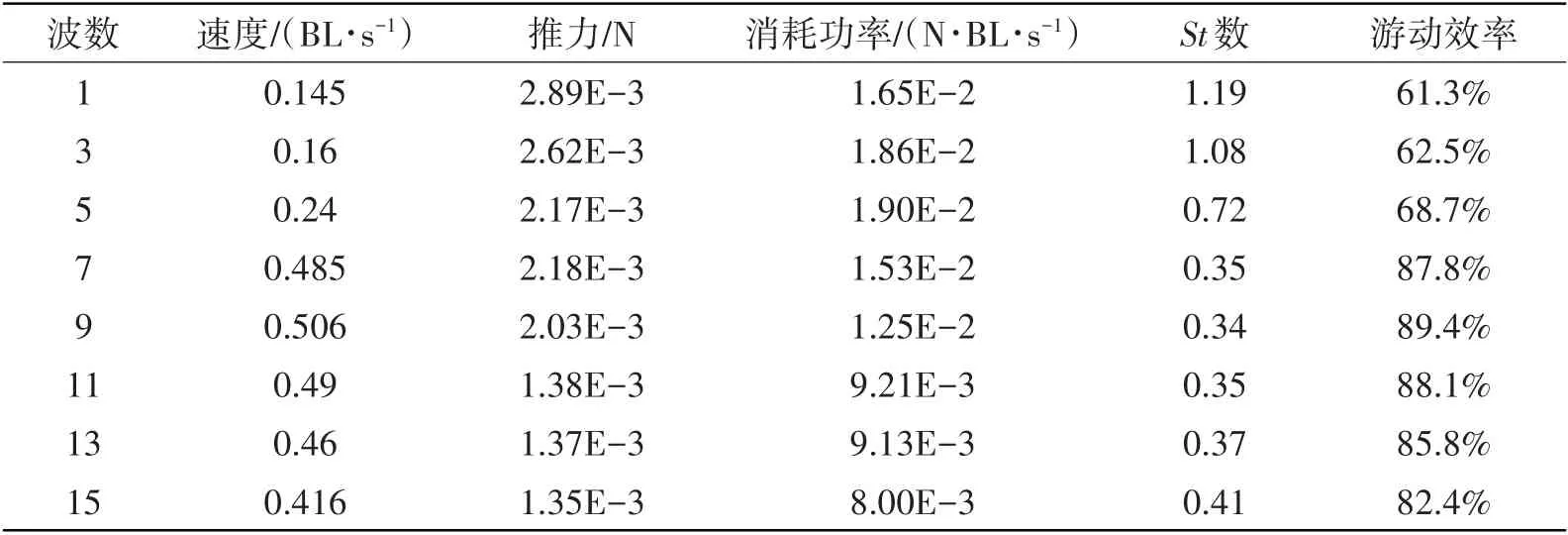
表4 鳗鲡科鱼类摆动波数对游动性能的影响Tab.4 Effects of wave number on swimming performance of anguilliform fish

3.3 鱼体外形与摆动曲线的匹配分析

在自然界中，鱼体选择不同外形和摆动曲线，为研究鱼体外形和摆动曲线的匹配关系，本节设置两类不同的算例，分别为：（1）保持鳗鲡科鱼类的外形，研究不同摆动曲线对游动性能的影响；（2）保持鳗鲡科鱼类的摆动曲线，研究不同外形对游动性能的影响。以鳗鲡科和鲹科鱼体为研究对象，通过人为选择不同外形和摆动曲线，研究了鱼类在游动过程中的优化选择，为探索鱼类快速高效游动机理的研究提供了依据。

3.3.1 鱼类摆动曲线对游动性能影响分析

保持鳗鲡科鱼体外形不变，设置两个算例：

（1）Re=600，鱼类采用鳗鲡科鱼类的运动学参数，如式（21）所示；

（2）Re=600，鱼类采用鲹科鱼类的摆动曲线参数，如式（22）所示。

当雷诺数Re=600 相同时，当鳗鲡科鱼体在其自然选择的运动学参数下，游动速度为0.847 BL/s，游动效率为71.2%。但鳗鲡科鱼类以鲹科鱼类的运动学参数运动时，对应的速度和效率均有所下降，对应游动速度和游动效率分别为0.436 BL/s和59.9%，该结果与鱼类自然选择结果相一致。

表5 鳗鲡科鱼类在不同运动参数下的游动性能Tab.5 Swimming performance of anguilliform fish under different kinematic parameters

3.3.2 鱼类外形对游动性能影响分析

鳗鲡科和鲹科鱼类的几何形状差异较大，鳗鲡科鱼体呈细长状，而鲹科鱼类为宽扁型。根据文献[21]，设鲹科鱼类的横截面为垂直于中性线的椭圆，椭圆的大小半径分别为R(x)和r(x)：

采用鳗鲡科鱼类的运动学参数（式(21)），鱼类外形分别采用鳗鲡科和鲹科鱼体外形，然后研究鱼体外形对游动性能的影响。对比表6和表7，在Re=500的流体环境中，与鲹科鱼类外形相比，鳗鲡科鱼类外形鱼类所对应的游动速度提高了13.24%，游动效率提高2.3%。在不同流体环境中，当鱼体波动形式为鳗鲡科模式时，鳗鲡科细长体外形更容易实现快速高效的游动性能。随着流体雷诺数的增加，鱼类外形对游动性能的影响依然存在着较明显差距，该结论证实了鱼类在自然界中通过特定外形和独特的鱼类的摆动曲线相配合，可以获得最优的游动性能。

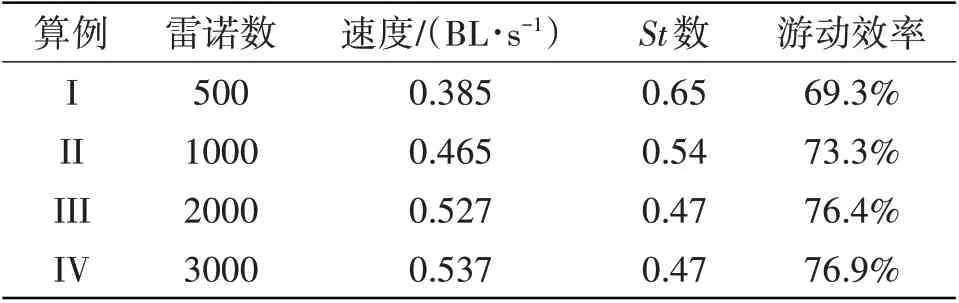
表6 保持鳗鲡科外形的鳗鲡科鱼类游动性能Tab.6 Swimming performance of anguilliform fish with the shape of anguilliform fish

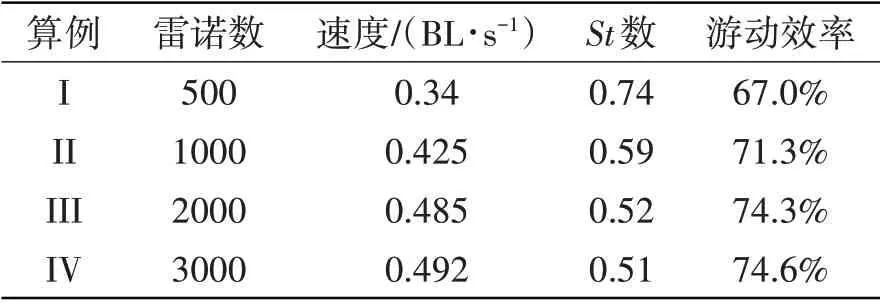
表7 具有鲹科外形的鳗鲡科鱼类游动性能Tab.7 Swimming performance of anguilliform fish with the shape of carangiform fish

以雷诺数3000为例，鱼类不同外形对应的涡量分布如图6所示，尾迹涡街结构主要通过尾迹长度χ和尾迹宽度ψ来描述。鳗鲡科鱼体外形涡街结构的平均尾迹长度为0.294，尾迹宽度为0.123，而鲹科鱼体外形对应的涡街结构平均尾迹长度和宽度分别为0.282 和0.109。结果表明，鳗鲡科鱼类外形更容易将尾迹的涡街结构长度和宽度进行扩展。结合涡动力学理论，该类型的涡街结构产生更大的推力[22]，与本文的数值结果相一致。

4 结 语

本文结合Level-set函数和浸入边界法的优势，采用数值方法建立了鳗鲡科鱼类的自由游动模型，根据Level-set 函数和重复初始化的过程来确定鳗鲡科鱼体界面，由基于直接力法的浸入边界法来决定鱼体与流体之间的相互作用力。通过改变鱼类的摆动曲线的频率、幅值和波数来分别研究鱼类在不同流体环境中的游动性能。通过设置不同鱼类的外形和摆动曲线参数，发现鳗鲡科鱼类的游动性能依赖于鱼类外形和摆动曲线参数的合理匹配。该研究对鱼类在自然界的优化选择提供了理论解释，也为通过控制鱼类的摆动曲线参数来实现水下航行器快速高效的推进性能提供指导。