基于直方图的数字化束流位置处理器检测方法
唐旭辉,高国栋,魏书军,曹建社,杜垚垚,刘 智,叶 强,麻惠洲,何 俊,季大恒,杨 静,李宇鲲,随艳峰,*,岳军会,*
(1.中国科学院 高能物理研究所,北京 100049;2.中国科学院大学,北京 100049)
束流测量系统是现代粒子加速器中不可缺少的系统,能监测带电粒子束团的位置和运动状态[1]。数字化束流位置处理器(DBPM)是束流位置监测(BPM)系统的核心模块,在硬件结构上主要由射频前端调理电路(AFE)和数字前端处理电路(DFE)组成。AFE用于对BPM感应电极拾取的微波信号进行幅度调控和滤波处理,DFE完成数字滤波、位置计算、频率抽取和数据传输。高速、高精度的模拟数字转换(ADC)电路是两者之间的桥梁,其转换精度将直接影响BPM位置测量的准确度和分辨率[2]。影响ADC转换精度的因素包含采样时钟抖动、ADC自身的孔径抖动、量化噪声及热噪声等[3],其中时钟抖动是指时域上时钟沿随机偏离理想位置的大小,随着信号频率的增加,由时钟抖动引起的误差也会变大。
中国科学院高能物理研究所研发了具有自主知识产权的DBPM[4],应用于BEPCⅡ工程,自研DBPM的ADC采样频率为116.115 152 MHz,束流信号中心频率为499.8 MHz,已达到高频范畴。此时高速、高精度的ADC电路对于时钟抖动非常敏感,因此在DBPM测试验收过程中准确地测量出ADC采样时钟的抖动是一个不可或缺的环节。关于ADC抖动的测量方法,Chiorboli等[5]利用相干采样拟合出孔径抖动与输入信号幅值或相位的关系,可消除量化噪声和微分非线性的干扰测量孔径抖动。Chaganti等[6]提出了用一对ADC分段采样作差的方法测量时钟抖动、孔径抖动。Virosztek[7]采用极大似然估计法计算正弦激励下的ADC孔径抖动。以上方法均取得了较好的效果,实际工程要完成大批量BPM电子学性能测试,既要准确地测量出ADC采样时钟抖动,又要减少BPM电子学整体测试时间。DBPM产品选用LTC2165高性能ADC芯片,具有16 bit的分辨率、76.8 dB的信噪比、550 MHz的模拟带宽和0.07 ps的超低孔径抖动[8],而时钟抖动比孔径抖动高出1个数量级,是主要关注对象,本文继承传统直方图法测量ADC孔径抖动的思想[9],提出应用于DBPM的直方图测量时钟抖动和ADC信噪比的方法。推导直方图计算时钟抖动和信噪比的原理,论证其检验DBPM-ADC各项指标的可行性,并分别用仿真和实验的方式验证直方图法的有效性,给出测量误差。
1 直方图检测DBPM的原理
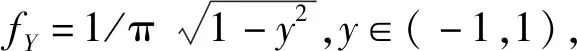
加速器系统中DBPM采样时间不是均匀分布的,而是相干带通采样,采样时钟与束流信号处于锁相的状态,导致正弦信号在时域上的某些值会被周期性的采集,被采点的分布与信号周期、采样周期和初相位有关。BEPCⅡ的高频频率为f=499.8 MHz,采样时钟频率为fs=116.115 2 MHz,f/fs≈99/23,即23个ADC采样周期中包含99个高频信号周期,如图2a所示。假设ADC是理想的,且信号初相位为0,此时23个不同的采样点数目相等,产生的直方图由23个等高的细线组成,如图2b所示。
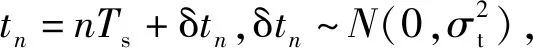
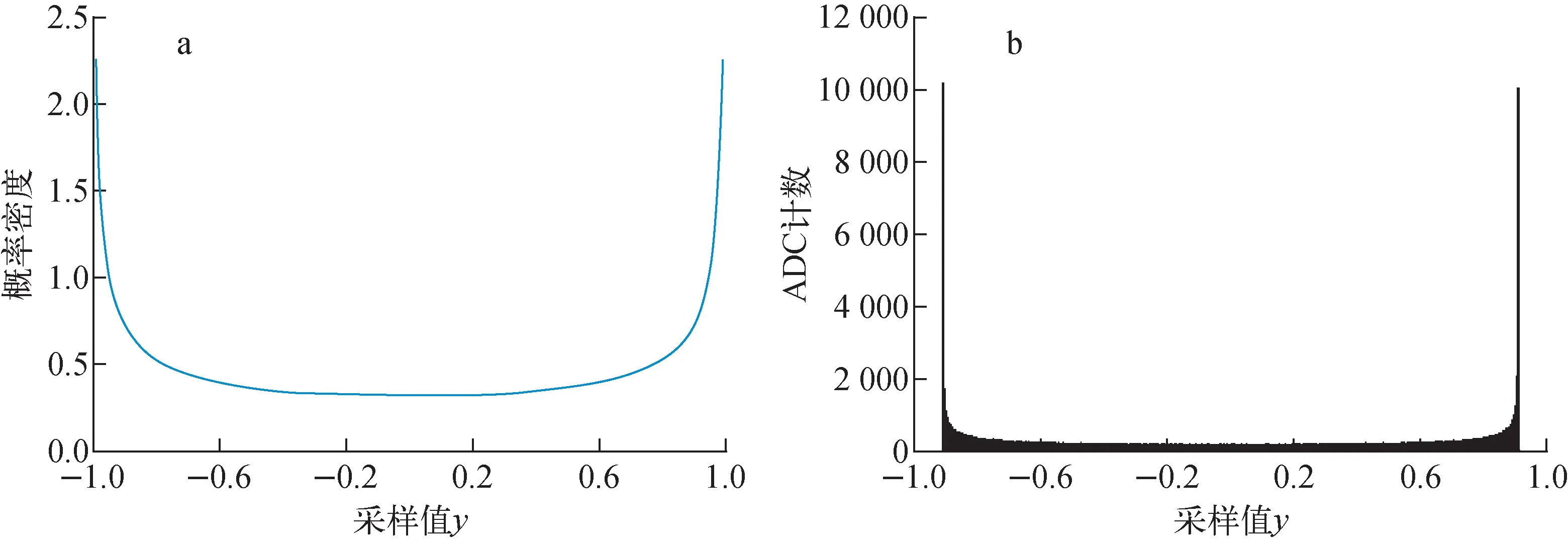
图1 ADC均匀采样的概率密度函数(a)和直方图(b)Fig.1 Probability density function (a) and histogram (b) of ADC uniform sampling
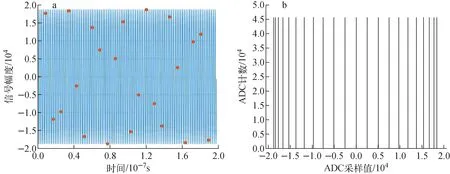
图2 理想ADC的时域采样点(a)和直方图(b)Fig.2 Time domain sampling point (a) and histogram (b) of ideal ADC
Xn=Vin(nTs+δtn)≈Vin(nTs)+
ωAcos(ωnTs+φ)δtn
(1)
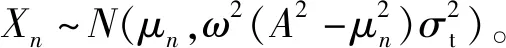
(2)
式(1)表明,用含高斯分布抖动的时钟序列进行采样,得到的ADC数据也服从高斯分布。由于相干采样带来的周期性,反应在直方图上是23个分立的高斯曲线峰。同一直方图上峰的高低与采样点的位置有关,越靠近零点采样,信号斜率越大,对抖动就越敏感,得到的峰也越矮胖。反之,越靠近极点采样,信号斜率越小,得到的峰也越高瘦,如图3所示。
图3b为正常工作的DBPM的ADC获取的直方图,由DBPM测试平台自动生成,可直观地检查锁相功能,因为只有在锁相的情况下,采样数据的直方图才是分立的峰,否则是图1b连续浴盆的形状。值得注意的是,在ADC采样点相位沿输入信号极值点对称时,23个采样点中有11对数据彼此相等,造成数据峰重叠,此时直方图上将只显示12个分立的峰。数据峰的重叠会引起数据分离困难,给测量结果带来很大的不确定性,因此在实际应用时不使用12个峰的直方图。
直方图中的23个或12个ADC采样峰幅值越高,表示ADC数据的信噪比越高,时钟的抖动越小。反之,时钟抖动大,ADC数据信噪比较差。直方图最左、最右端的数据是采样样本的最大值和最小值,如果时钟抖动的范围能够包含极值点的采样时刻,那么数据的最大/最小值就是信号幅值。在大多数情况下,前者可近似等于后者。因此,信号幅值A可直接在直方图中读出。
在进行抖动计算时,应当选择非零点和非极点对应的数据峰,统计其均值μ和方差σ,代入式(2)即可求出σt。假设ADC具有足够的分辨率,时钟抖动是决定信噪比(SNR)的唯一因素,此时信噪比可由式(3)估计[10]:
SNR=-20lg(2πfσt)
(3)
2 直方图检验法的仿真验证
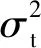
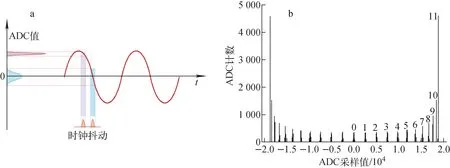
图3 含时钟抖动ADC的相干采样示意图(a)和采样后的直方图(b)Fig.3 Coherent sampling diagram of ADC with clock jitter (a) and histogram after sampling (b)
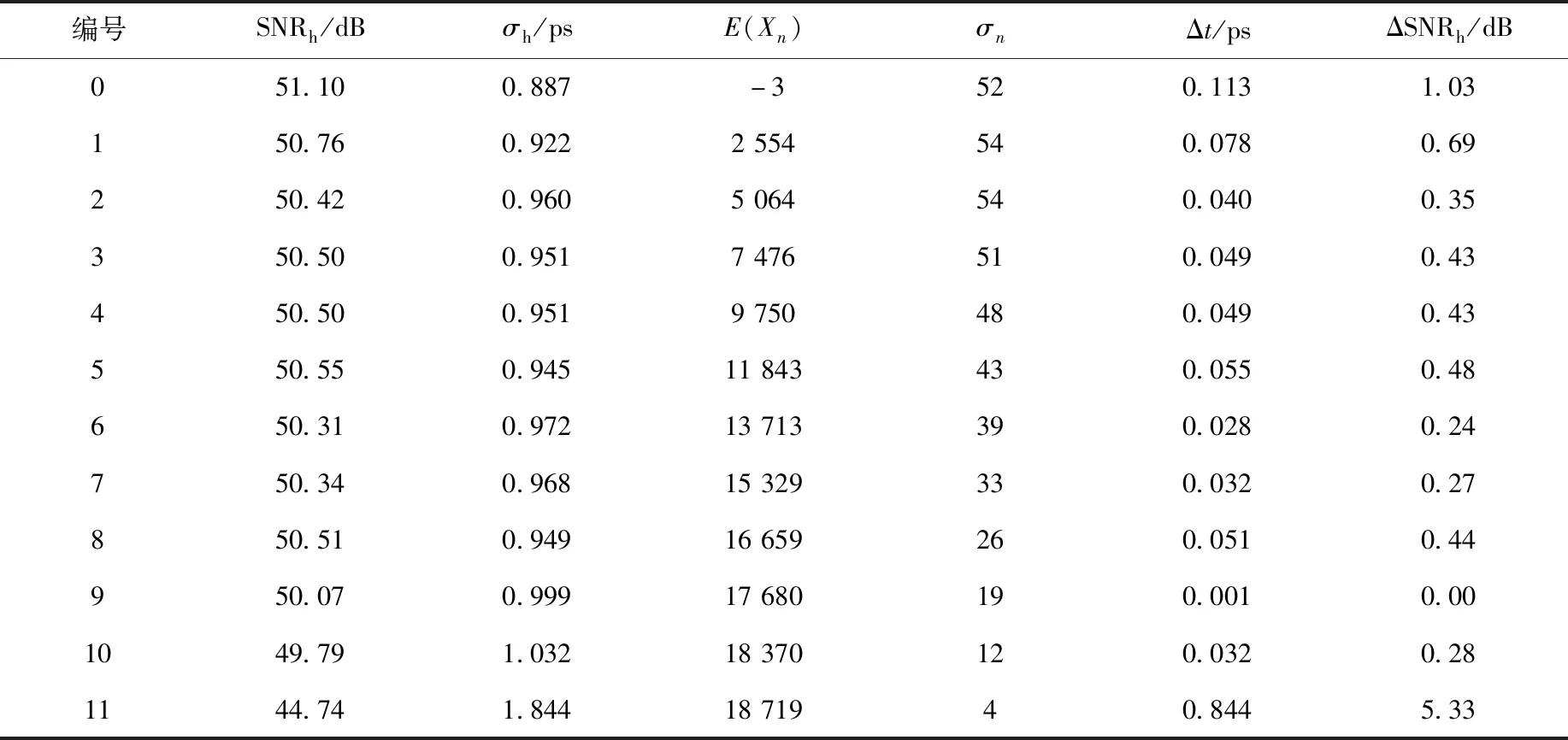
表1 12组仿真数据计算得到的ADC采样时钟抖动和信噪比Table 1 ADC sampling clock jitter and SNR calculated from 12 sets of simulation data
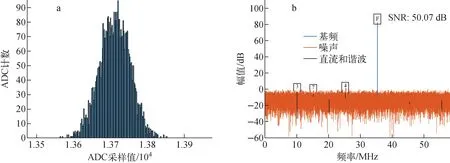
图4 1组采样数据的直方图(a)和MATLAB生成的频谱图(b)Fig.4 Histogram of a set of sampled data (a) and spectrum diagram generated by MATLAB (b)
表1中,第10组和第11组数据因为离信号极点很近,时钟抖动和数据标准差不能形成良好的线性映射,且对相位φ的变化更敏感,因此不采用。前3组数据的标准差非常接近,这是因为信号的频率很高,零点附近的信号曲线较陡,近似一条直线,这3处的时钟抖动被几乎相同的斜率映射。在标准差相近的情况下,由于零点处的采样数据均值接近0,代入式(2)计算时分母偏大,使得结果明显偏小,所以第0组计算的误差也较大。综合以上因素,宜选用编号为2~8之间的数据来计算时钟抖动和信噪比。以第6组数据为例进行展示,其直方图如图4a所示,均值为13 713,标准差为39。图4b为用MATLAB自带的snr()函数对采样数据进行处理生成的频谱图,其中信号频率为35.34 MHz,这是带通采样将499.8 MHz的信号进行频率搬移的结果[11]。仿真结果表明,在数据选取合适的情况下,直方图法获得的抖动与信噪比误差很小,其检测结果是可靠的。
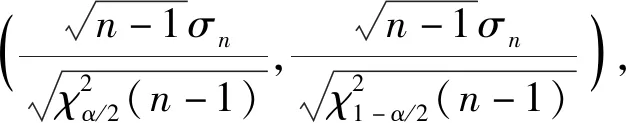
3 直方图检验法的实验验证
为进一步验证直方图法在工程实践中的可行性,搭建了一套DBPM测试平台,结构如图5所示,主要由PC机、测试激励信号源(KEYSIGHT MXG N5181B,9 kHz~6 GHz)、参考时钟信号源(ROHDE & SCHWARZ SMF100A)、一分四功分器(ZFSC-4-1-S+)、自行研发的时钟消抖/扇出模块、高性能相噪分析仪(KEYSIGHT信号源分析仪E5052B,10 MHz~7 GHz)、网络交换机(TL-SF1008D)和待测的DBPM组成。PC机是系统的控制中心,可通过网络交换机与信号源和DBPM进行通信。测试信号源输出的正弦信号首先经功分器生成同源等幅值的4路信号,经同轴电缆输入DBPM端口。为保证测试信号和参考信号是锁相的,两个信号源之间需设置10 MHz相位同步。DBPM-DFE板卡的核心是1块Xilinx Zynq芯片,它能将4路模拟信号ADC采样后的原始值保存在1个txt文本中,PC机可通过SSH的方式将存有原始ADC数据的文本传输至本地处理和分析。AFE的晶振时钟会与外部1.262 MHz触发信号通过时钟管理芯片进行变频和锁相,最终输出约116 MHz的采样时钟信号给ADC芯片,并通过1个微型SMA接头与相噪分析仪相连。实验结果显示,直方图法的测试时间小于1 min,满足批量测试的需求。
通过该测试平台获取直方图、MATLAB标准函数和相噪分析仪的测试结果,将三者进行对比。这是因为信号源输出的激励信号品质较高,抖动低至70 fs,对应信噪比高达73 dB。实验室环境温度稳定,射频调理电路的滤波器和放大器贡献的噪声很小[12-14],经调理后的信号信噪比仍然高达70 dB,且ADC芯片孔径抖动仅有70 fs,也可忽略不计。因此,射频前端和ADC引入的噪声相对于时钟相噪很小,理论上直方图和MATLAB标准函数测量的结果不会明显比相噪分析仪偏大,将3种方法测量结果进行对比来论证直方图法的可行性是合理的。
设定测试信号源为输出频率499.8 MHz、幅度8 dBm的正弦信号,AFE数字衰减器的衰减值为24 dB,采样点个数为10万,获取4路原始采样数据并传输至PC机,并用MATLAB绘制为直方图。为避免重叠的数据峰造成统计异常,在抖动计算时不使用12个峰的直方图。以其中1次测量为例进行展示,MATLAB生成的直方图和频谱图如图6所示。设置相噪分析仪的频率偏移为1 kHz~10 MHz,测量的时钟相位噪声谱如图7所示,其中抖动的均方值为603 fs。
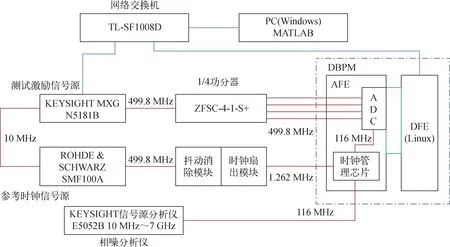
图5 DBPM测试平台Fig.5 DBPM test platform
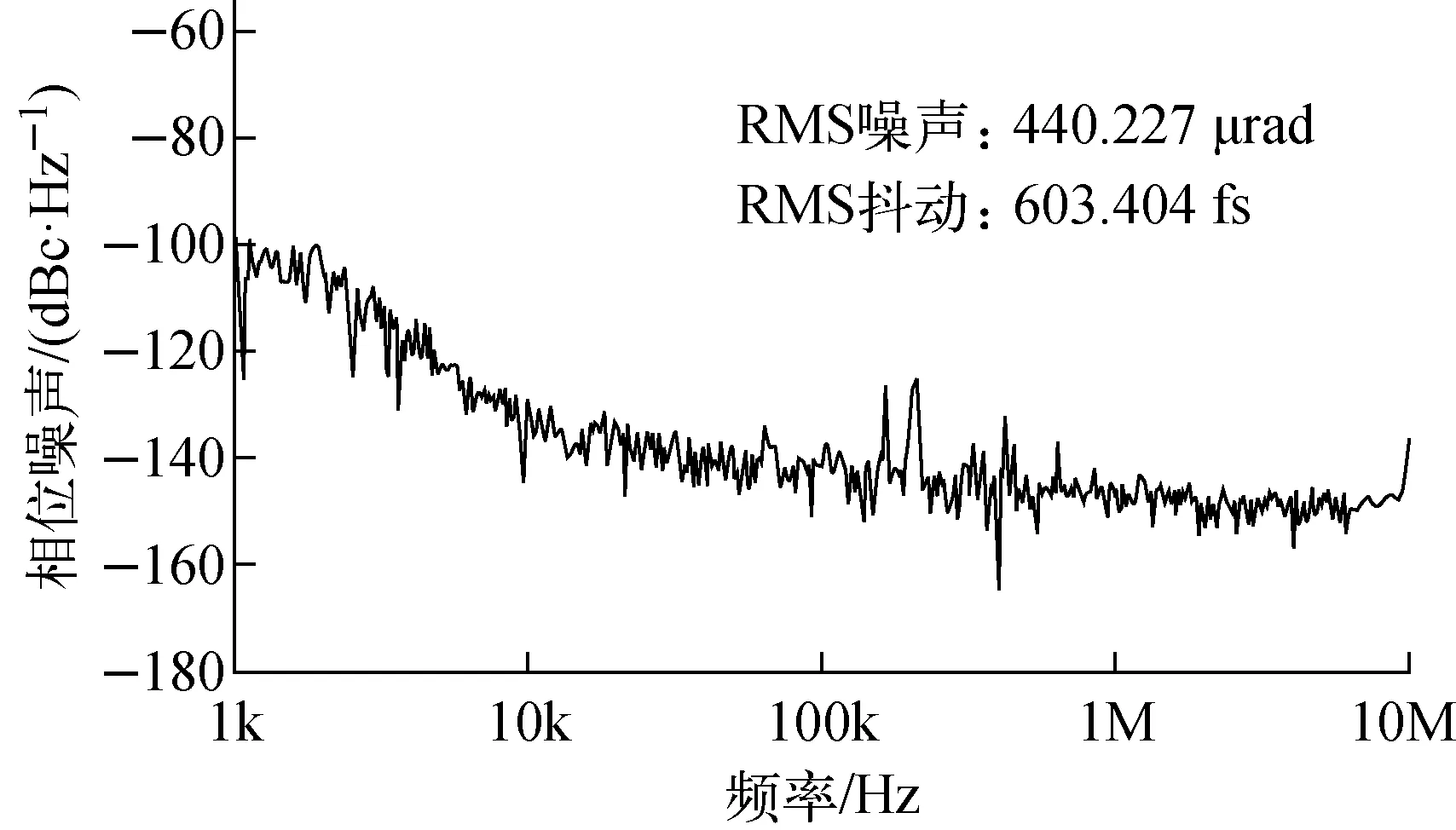
图7 相位噪声谱Fig.7 Phase noise spectrum
由图6b可知,MATLAB标准函数计算的ADC信噪比SNRm=56.79 dB,代入式(3)求出MATLAB标准函数下的抖动σmt=0.461 ps。抽取6台DBPM,按照上述实验流程,得到每台DBPM直方图法测量的抖动σht、相噪分析仪测量的抖动σpt和直方图法测量的信噪比SNRh。以SNRm和σmt为参考真值,计算直方图测量抖动的绝对误差Δth,相噪分析仪测量抖动的绝对误差Δtp以及直方图法测量信噪比的绝对误差ΔSNRh。实验数据和计算结果列于表2。
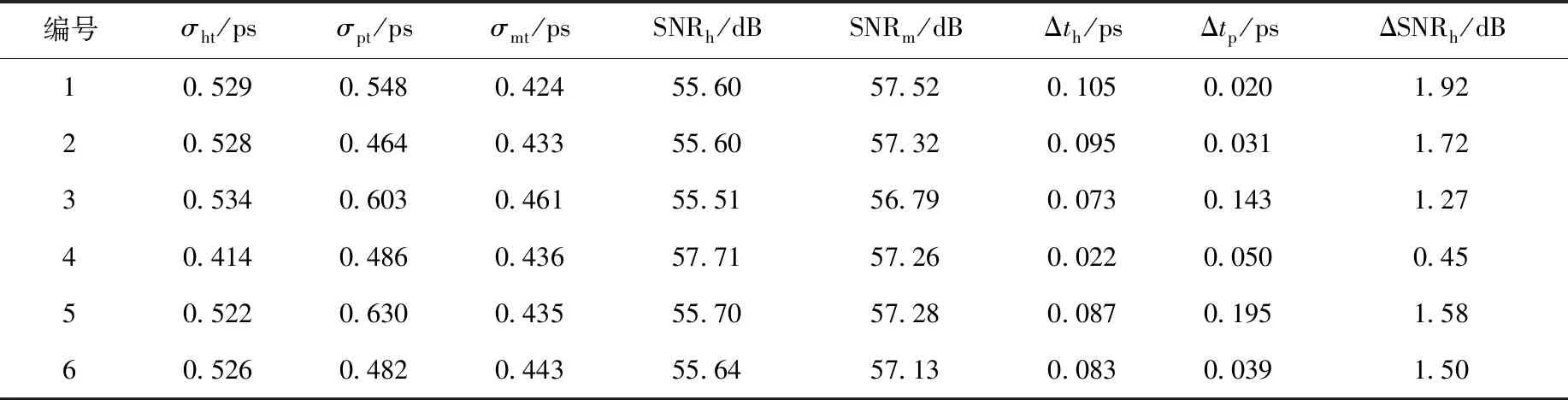
表2 6台DBPM-ADC的测量结果Table 2 Measurement result of 6 DBPM-ADCs
通过实验可发现,直方图法测量的抖动绝对误差很小,约为100 fs,与高精度相噪分析仪测量的结果非常接近。直方图法测量的信噪比绝对误差在2 dB以内。考虑到时钟抖动本身属于非常微小的物理量,需要高精度的仪器和复杂的设备才能得到精确的结果,而DBPM的产品化批量测试对测量速度要求相对较高,对测量精度要求相对较低,在这种前提下,直方图法是一种简单、稳定、高效又不失准确性的方法。如果将采样数据量增大1个数量级,即100万个数据,此时MATLAB标准函数计算的信噪比基本保持不变,但直方图法求得的信噪比会显著减小。分析其原因为:BEPCⅡ的DBPM选用的AD9510时钟管理芯片内部锁相环,在实际工作中的锁相位置是在不断调整的,在较长的采样时间内,抖动本身很小,总体的信噪比基本不变,然而由于锁相位置发生变化,得到的单组数据直方图出现多个峰的形状,使计算的标准差变大,进而使得抖动偏大。因此,在较短的采样时间内,锁相位置没有发生变化,采集少量但足够的数据,直方图法可准确反映时钟抖动的情况。
4 结论
本文针对BEPCⅡ和HEPS的DBPM的生产测试需求,提出了一种用直方图测量DBPM ADC采样性能的方法。该方法不仅为DBPM ADC性能评估提供了理论依据,同时也可用于对DBPM电子学的性能进行检验。ADC采样数据的直方图是否分立可判断采样时钟是否锁相。直方图的最大/最小值可获取输入信号的幅值,判断ADC是否饱和。直方图中孤立数据峰的统计量可计算ADC时钟抖动和信噪比。通过MATLAB仿真和实验测量两种方式,验证了该方法的可行性。仿真结果显示,直方图法的测量原理是正确的,测量结果与理论值基本一致。在BEPCⅡ和HEPS的DBPM采样抖动要求范围内,可使用直方图法进行评估。