基于NSGA-Ⅱ算法的核反应堆功率LQG控制器设计

金 鑫，李东原，秦 戈，徐教珅，唐 辉，王 鑫

(中广核工程有限公司 核电安全监控技术与装备国家重点实验室，广东 深圳 518172)

核电作为可大规模应用的清洁能源，在替代化石能源、减少碳排放和改善空气质量等方面发挥着越来越重要的作用。作为核电厂的核心，堆芯不仅是核电厂的主要热源，也组成了放射性核燃料的重要包容屏障。因此，核反应堆堆芯的有效控制，在提高核电厂运行灵活性，确保核安全等方面具有重要的研究意义。

核反应堆堆芯是一个非线性、时变、多输入多输出的复杂系统，其控制问题一直以来都是核电技术中的热点和难点。为提高堆芯控制性能，国内外许多学者进行了广泛而深入的研究。Kerlin等[1]提出了可自动优化反应堆控制系统控制器的设计方法，结果表明该方法无需耗费大量计算即可获得优越的控制效果。Morita等[2-3]提出了机械补偿(MSHIM)运行控制模式，能实现不调硼负荷跟踪运行，提供更出色的控制性能。Edwards等[4-5]提出了基于堆芯的状态反馈辅助控制方法(SFAC)，该方法保留了一个经典输出反馈控制环节，并利用状态反馈修改参考负荷信号，以便得到期望参考输入，结果表明状态反馈能改善系统性能，而经典输出反馈能改善稳定性和鲁棒性。为改善堆芯燃料温度和冷却剂出口温度在经受负荷大范围变化时期望的动态性能，Ben-Abdennour等[6]利用带有回路传输恢复的线性二次型高斯(LQG/LTR)控制理论设计了堆芯鲁棒控制器，仿真结果表明所设计的控制器可在较宽范围改善温度控制性能。Hah等[7-8]将模糊控制逻辑用于反应堆负荷跟踪运行控制，并证明了其可行性。Upadhyaya等[9]应用多变量自适应算法控制堆芯轴向功率分布，计算结果表明该算法响应速度很快。Uluyol等[10]提出了局部内存多层Gamma反馈(LOGF)神经网络方法，该方法能很好地用于辨识、预测和控制，提供了更强的跟踪负荷的能力，改善了燃料温度和堆芯出口温度的控制效果。Arab-Alibeik等[11]将LQG/LTR应用于SFAC结构的反应堆输入控制，改善了温度控制效果。Na等[12]设计了负荷跟踪运行的模预测控制器，以改善反应堆功率水平和功率分布的控制，仿真结果表明该控制器具有很快的响应能力。Dong等[13]提出了基于非线性观测器的反馈耗散控制方法，计算结果表明该方法具有较高的负荷跟踪运行控制性能。此外，董哲等[14-15]还设计了比例积分功率水平控制器、非线性动态输出反馈控制，以提高反应堆功率水平控制能力。西安交通大学Wei等[16-26]也对堆芯控制系统进行了研究，发表成果主要有堆芯功率的PID控制、鲁棒控制、解耦控制以及控制系统的参数优化等。上述研究都分别应用不同方法、从不同方面对反应堆功率控制进行了有益探索，具有重要的研究意义。

随着核电技术的不断发展，人们对反应堆功率控制提出了新的更高的要求，如在移动更少的控制棒步数(即花更少的代价)的前提下获得更优越的堆芯功率控制性能。作为最优控制的LQG方法具有计算量小、控制器结构简单、系统鲁棒性好等特点，在工程应用中价值很高[27-28]。对于LQG最优控制方法，性能指标中权重矩阵的选择对控制系统的性能有很大影响。通常权重矩阵是根据系统的物理过程人为设置的，它需要对系统有比较充分地了解与经验才能确定。因此，这样的“最优”事实完全是主观人为的。如果权重矩阵选取不当，虽然可以解出最优解，但这样的最优解没有实际意义。另外，加权矩阵的选择过度依赖于设计者的经验，需要设计者根据系统输出逐步调整加权矩阵，直到获得满意的输出响应值，这样不仅费时，而且无法保证最优的权重矩阵，因此获得最优控制反馈系数不能保证使系统达到最优。遗传算法NSGA-Ⅱ在多目标优化过程中，因其具有良好的寻优性，并克服了单纯形法对参数初值的敏感性的优势，应用比较广泛，且取得了良好的寻优效果[29-30]。因此，本文首先设计反应堆功率水平的LQG控制器，并基于NSGA-Ⅱ算法，对LQG控制器性能指标的权重矩阵进行多目标优化，以提高反应堆功率LQG控制器的设计效率和性能。

1 堆芯模型

建立堆芯模型的方法主要有：点堆堆芯建模、一维堆芯建模、多节点堆芯建模、三维堆芯建模、基于智能辨识算法的堆芯建模等。由于本研究主要关注堆芯功率水平的控制，而不关心功率分布情况，因此点堆模型已满足要求。为简化模型，提高仿真计算速度，本文将基于点堆模型进行控制系统设计与控制参数优化。

1.1 非线性模型

由于本文研究的瞬态过程仿真时间较短(以s为单位)，因而可忽略碘氙的变化，此时非线性点堆模型可总结如下：

(1)

(2)

(3)

(4)

(5)

ρ=ρrod+αf(Tf-Tf0)+

(6)

式中：nr为归一化堆芯功率；cri为归一化第i组缓发中子先驱核浓度；Λ为中子代时间，s；ρ为总反应性，pcm；β为缓发中子总份额；βi为第i组缓发中子份额；λi为第i组缓发中子衰变常量，s-1；Tf为燃料平均温度，℃；Tf0为燃料初始平均温度，℃；f为燃料中产生热量占总功率的份额；P0为反应堆满功率，W；μf为堆芯燃料的总热容量，J/℃；Ti为堆芯入口冷却剂温度，℃；Ti0为初始堆芯入口冷却剂温度，℃；To为堆芯出口冷却剂温度，℃；To0为初始堆芯出口冷却剂温度，℃；Ω为燃料和冷却剂间的换热系数，W/℃；M为冷却剂的质量流率乘以热容量，W/K；μc为堆芯冷却剂的总热容量，J/℃；ρrod为控制棒移动引入的反应性，pcm；αf为燃料反应性温度系数，pcm/℃；αc为冷却剂反应性温度系数，pcm/℃；vrod为以每秒移动距离占堆芯长度比例表示的控制棒棒速；Gr为单位长度上控制棒的总反应性价值，pcm。

1.2 线性化模型

根据微扰理论，对1.1节的非线性模型进行线性化处理，并求得线性时不变模型。采用单组缓发中子模型和堆芯冷却剂入口温度为常值，对式(1)～(6)进行线性化处理，得：

(7)

(8)

(9)

(10)

(11)

δρ=δρrod+δρf=δρrod+αfδTf+

(12)

依据式(7)～(12)，求得瞬态堆芯单输入单输出状态方程：

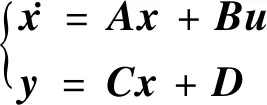
(13)

依据式(7)～(12)，求得瞬态堆芯单输入单输出传递函数：

(14)

堆芯状态方程和传递函数之间的关系式为：

(15)

式中：u=δρ为输入量；y=δnr为输出量；x=[x1,x2,x3,x4,x5]T=[δnr,δcr,δTf,δTo,δρrod]T为5×1状态变量阵；A为R5×5系统矩阵；B为R5×1输入矩阵；C为R1×5输出矩阵；D为R1×1零矩阵。

A、B、C和D的表达式如下：

A=

(16)

(17)

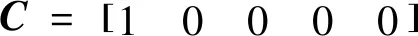
(18)

D=[0]

(19)

2 控制器设计与优化

2.1 LQG控制器设计

LQG控制器由Kalman状态估计器和1个最优状态反馈增益器组成。因此，求解LQG控制器就是求解Kalman滤波器增益矩阵和LQR增益矩阵。

1) 求解Kalman滤波器问题

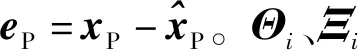
PfAT+APf-PfCTR-1CPf+ΓQΓT=0

(20)

在选择合适的Γ、Q和R之后，求解Kf，使得Pf是式(20)的解。所求解Kf的表达式为：

Kf=PfCTR-1

(21)

式中，Kf=[kf1kf2kf3kf4kf5kf6kf7]T为R7×1的矩阵。

2) 求解LQR问题

求解LQR问题就是求解LQR增益矩阵Kc。

考虑式(22)所示的最优性能指标：

(22)

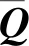
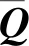
(23)

式中：Kc=[kc1kc2kc3kc4kc5kc6kc7]为R1×7的矩阵；Pc为实对称半正定矩阵，且为Riccati方程式(24)的解。

(24)

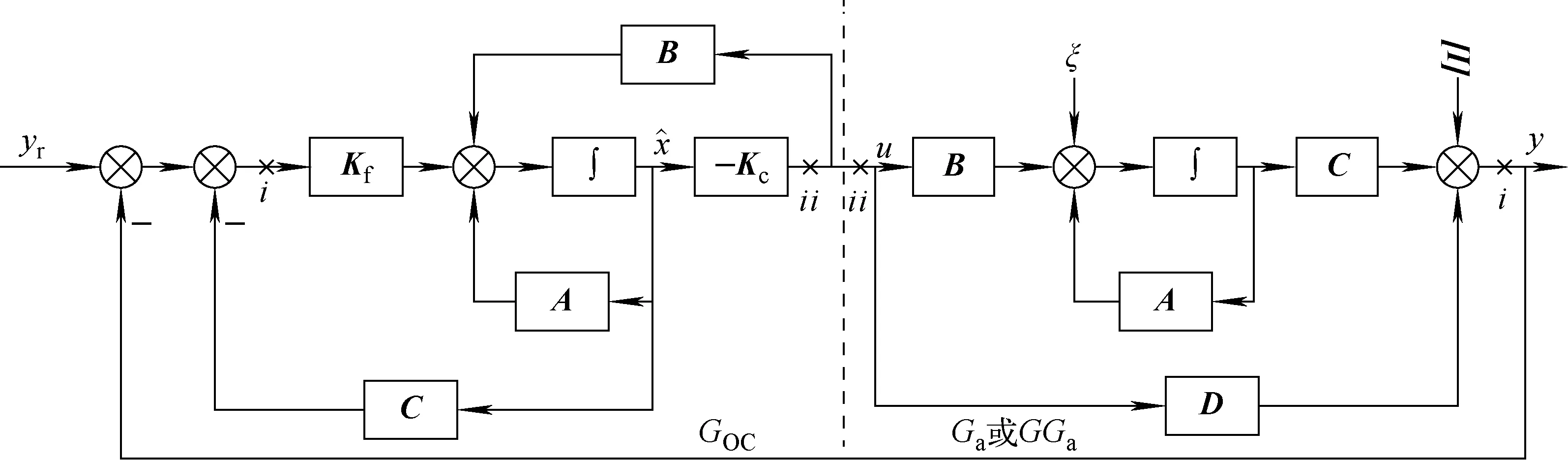
图1 LQG 控制器结构示意图Fig.1 Schematic diagram of LQG controller structure

2.2 控制器优化

LQR权重系数的选取具有一定的主观性，对设计人员的经验要求较高，且选取效率较低，不一定能选出最优的权重值。而遗传算法NSGA-Ⅱ具有较好的全局寻优能力。因此，本文采用NSGA-Ⅱ对LQR的权重系数进行优化设计。

1) NSGA-Ⅱ算法

NSGA算法于1994年由Srinivas和Deb[31]发表。2002年，Deb将其改进为带精英策略的非支配排序遗传算法(NSGA-Ⅱ)[29-30]，使之成为经典的多目标优化算法之一。NSGA-Ⅱ具有运行效率高、解集的分布性良好等优点，尤其在低维优化方面具有较好的优化性能，因而一经提出便广受关注，迄今已被国内外学者引用26 000余次，广泛应用于诸多领域的研究。因此，研究应用经典的NSGA-Ⅱ算法对核电站控制系统进行多目标参数优化具有重要的研究意义与应用价值。

详细的NSGA-Ⅱ算法可参考文献[30]，其计算流程如图2所示。

2) 优化对象与目标函数

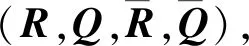
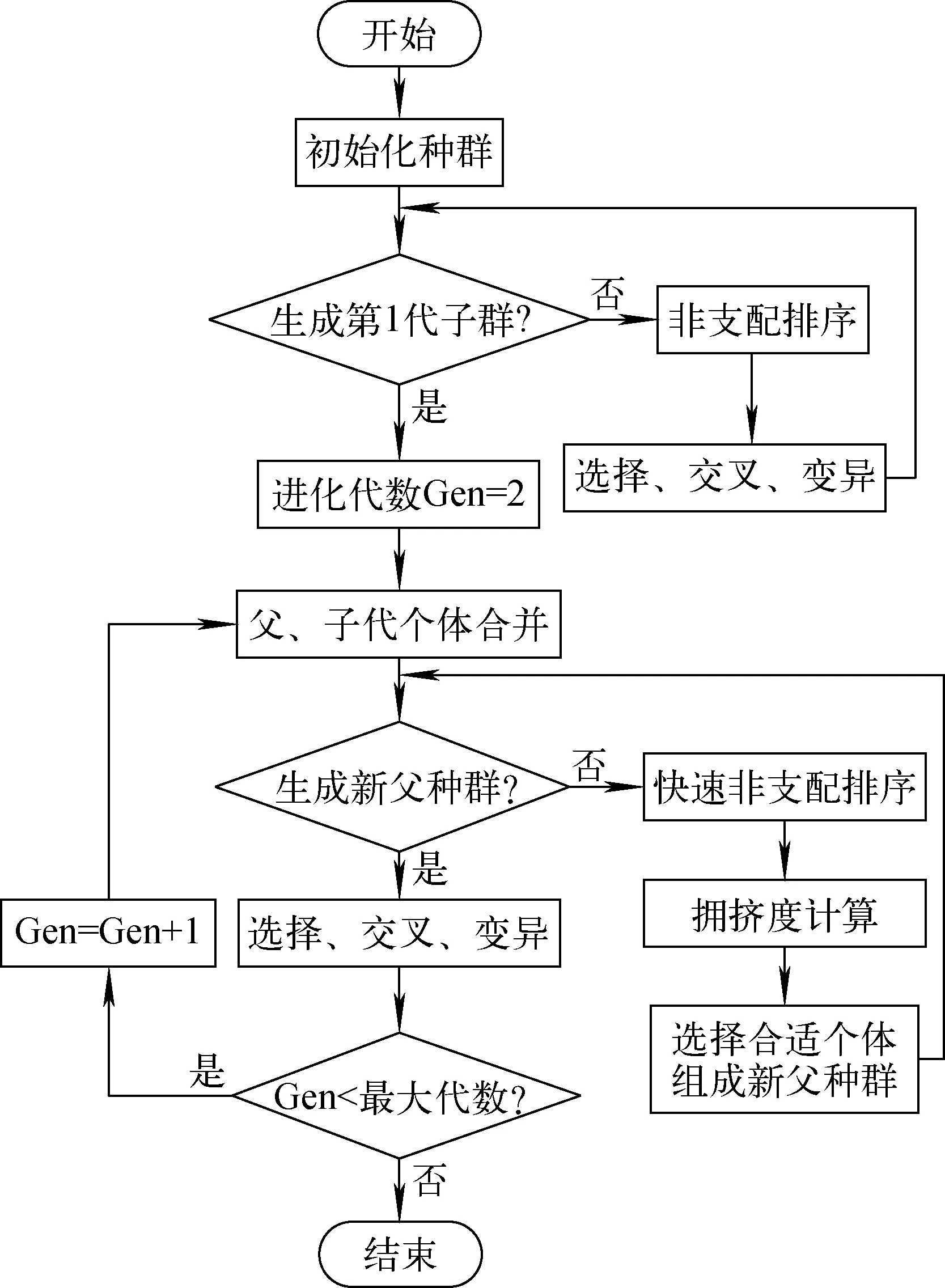
图2 NSGA-Ⅱ算法流程图Fig.2 NSGA-Ⅱ algorithm flow chart

通过调整LQG控制器的LQR权重参数，使目标函数取得极值，即可实现优化设计。目前，常用的目标函数建立方法有加权性能指标型和误差积分型两类，而误差积分型则又可细分为误差平方积分(ISE)、误差绝对值积分(IAE)、时间乘以误差绝对值积分(ITAE)、时间与误差平方之积的积分(ITSE)、时间平方与误差绝对值之积的积分(ISTAE)和时间平方与误差平方之积的积分(ISTSE)。当控制系统参数变化时，ITAE能很容易地辨识出最小值，更易区分系统的性能，而且ITAE相比于其他指标能使优化后的系统具有更小的超调量和震荡[32-33]。本文研究的是反应堆功率P与控制棒行程S的两目标参数优化问题，因而可采用ITAE评价标准建立如下目标函数：

(25)

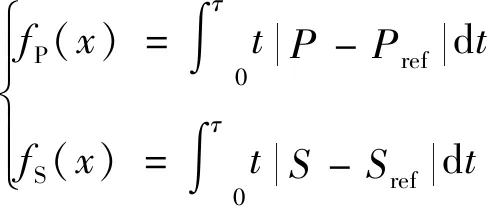
(26)

式中：τ为仿真时间，s；P、Pref为归一化实际功率与参考功率；S、Sref为控制棒实际行程与参考行程，m。

3) 优化设计

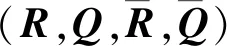
表1 堆芯主要参数Table 1 Main parameters of reactor core

图3为采用NSGA-Ⅱ算法求解得到的Pareto最优解集，横纵坐标分别表示Pareto最优解集中的目标函数fP(x)与fS(x)。从图3可看出，在Pareto最优解集中，目标函数fP(x)在2.85～50.51的范围内变化，而fS(x)的变化范围是10.39～11.84。目标函数fP(x)与fS(x)的最优解存在矛盾，即目标函数fP(x)取最小值时，fS(x)处于最大值处，反之亦然。因此，不能同时获得反应堆功率和控制棒行程的最佳控制性能。

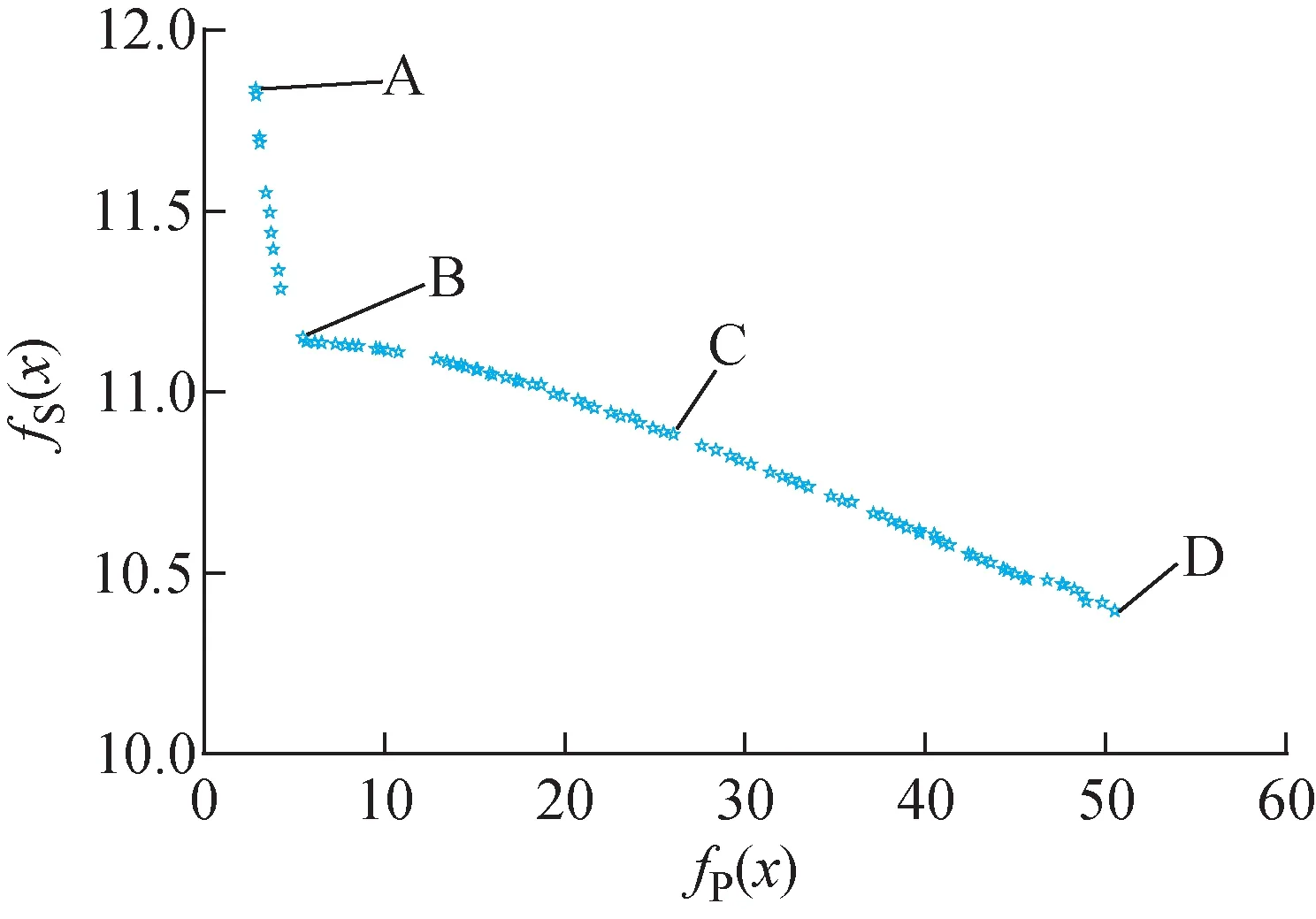
图3 Pareto最优解集Fig.3 Pareto front

将上述4点分别代入所设计的LQG控制器，对100%FP-90%FP阶跃降负荷工况进行仿真分析，结果如图4所示。

从图4可看出，采用NSGA-Ⅱ算法优化所得的Pareto前沿中的A、B、C和D 4点所对应的LQR权重系数的堆芯功率LQG控制器，在100%FP-90%FP阶跃降负荷工况下均能获得较好的控制效果，反应堆功率在瞬态发生后在较短时间内稳定在参考值附近，堆芯出口温度也很快地降至新的稳定状态。同时，最优点A所对应的LQG控制器的堆芯功率控制效果最好，在阶跃瞬态发生后能迅速将反应堆调整到参考值附近，超调量很小，稳态误差最小，堆芯出口温度也相应地被快速降至新的稳态。从图3可看出，A点对应的LQG控制效果最好的原因是，A点的堆芯功率控制优化适应度函数fP(x)最小，表明该点的堆芯功率控制效果最好，但该处的控制棒行程优化适应度函数fS(x)最大，因此A点对应的LQG控制器在瞬态过程中的控制棒行程比B、C、D点更长，将对控制棒寿命产生一定的不良影响。但值得注意的是，控制棒行程优化适应度函数fS(x)总的变化范围很小(10.39～11.84)，总体上控制棒行程的差异对控制棒寿命的影响不大。因此，在后续研究中，为获得最优的堆型功率控制效果，推荐采用A点所对应权重系数的LQG控制器进行堆芯功率控制。

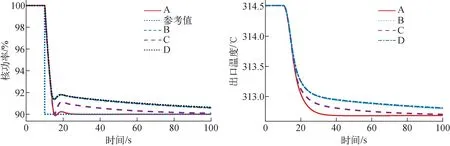
图4 不同权重系数下100%FP-90%FP阶跃负荷仿真结果Fig.4 100%FP-90%FP step load simulation results of different weight factors

3 仿真分析

本文在上述研究的基础上，分别对不同功率水平下的不同瞬态工况进行了仿真研究，在相同初始条件下将本文所设计的LQG控制器与传统PID控制器所得仿真结果进行对比，以验证本研究所设计的优化权重系数的LQG控制器在不同工况下控制性能的优越性，仿真的工况如下。

1) ±10%FP阶跃负荷工况：90%FP-100%FP、40%FP-30%FP阶跃负荷和30%FP-40%FP阶跃负荷工况；

2) ±5%FP/min线性变负荷工况：100%FP-30%FP/-5%FP/min线性负荷和30%FP-100%FP/+5%FP/min线性负荷工况。

上述工况，本文设计的LQG控制器均采用A点所对应权重系数进行堆芯功率控制，其中，阶跃负荷工况的仿真时间为100 s，而线性变负荷工况的仿真时间为1 000 s，仿真结果如图5～10所示。

从图5～8可看出，阶跃负荷瞬态发生后，本文设计的LQR控制器能使反应堆功率迅速调节到参考值附近，调节速度较快，调节时间较短，且都能稳定在参考值附近。同时，堆芯出口温度也能较快地调节到新的稳定状态，调节时间短，超调量小，且稳定性好。这表明了本文设计的反应堆功率LQG控制器在高功率和低功率水平下均具有较好的控制性能和鲁棒性。值得注意的是，本文设计的LQG控制器虽然都能满足高功率和低功率阶跃负荷瞬态的堆芯功率控制，但也可看出，本文的LQG控制器在低功率阶跃负荷工况下的控制效果略差于高功率阶跃负荷工况的控制效果，这主要由于本文采用的是在高功率阶跃负荷(100%FP-90%FP阶跃负荷)工况下优化设计得到的LQR权重系数。如针对低功率工况进行优化设计，预计能在低功率工况下获得更好的控制效果。尽管如此，本文设计的LQG控制器不管在高功率还是在低功率下的阶跃负荷工况，所获得的控制效果均能满足堆芯功率控制的要求，且具有较好的鲁棒性。

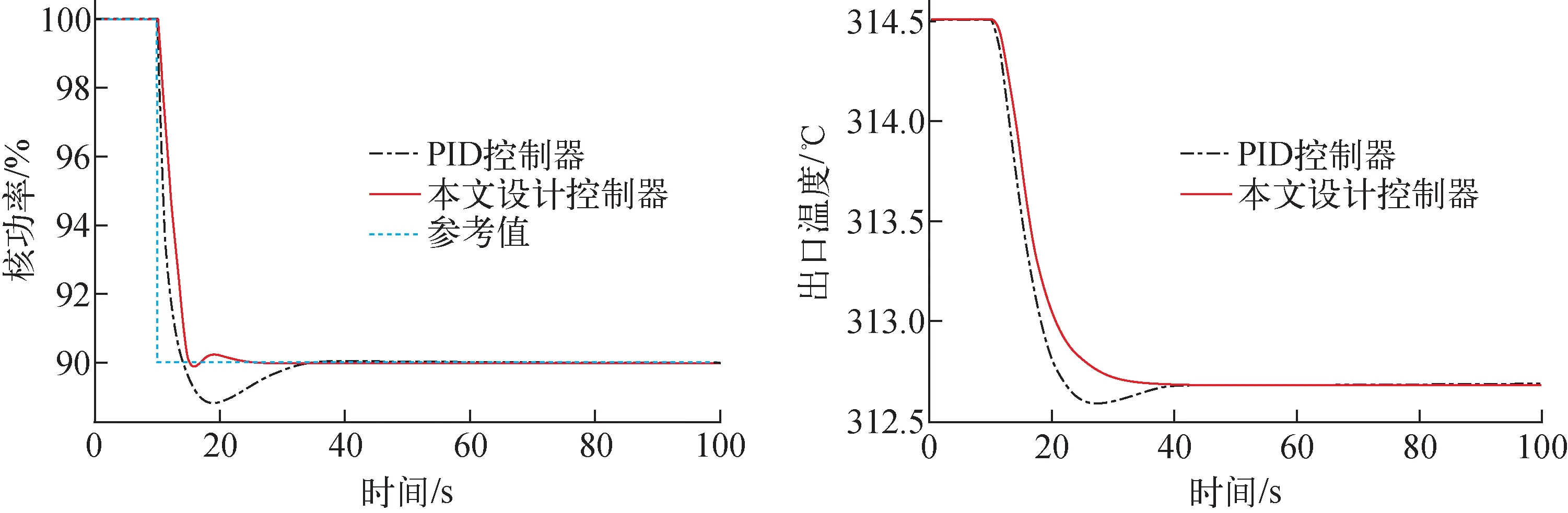
图5 100%FP-90%FP阶跃负荷仿真结果Fig.5 100%FP-90%FP step load simulation results

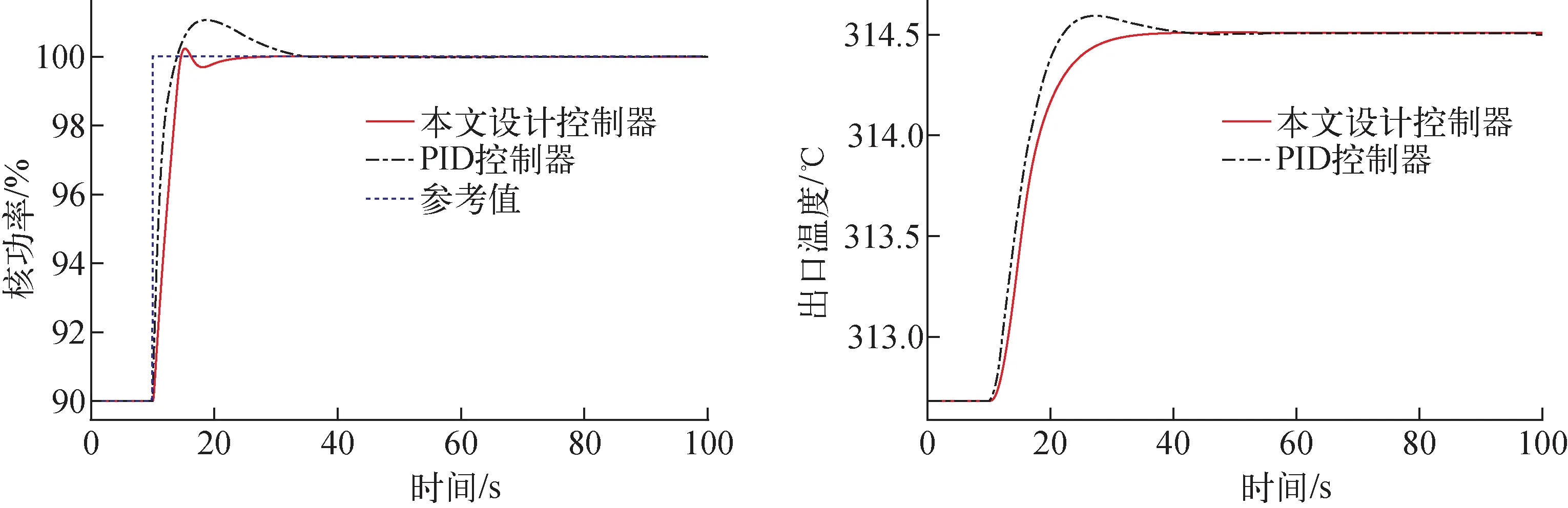
图6 90%FP-100%FP阶跃负荷仿真结果Fig.6 90%FP-100%FP step load simulation results

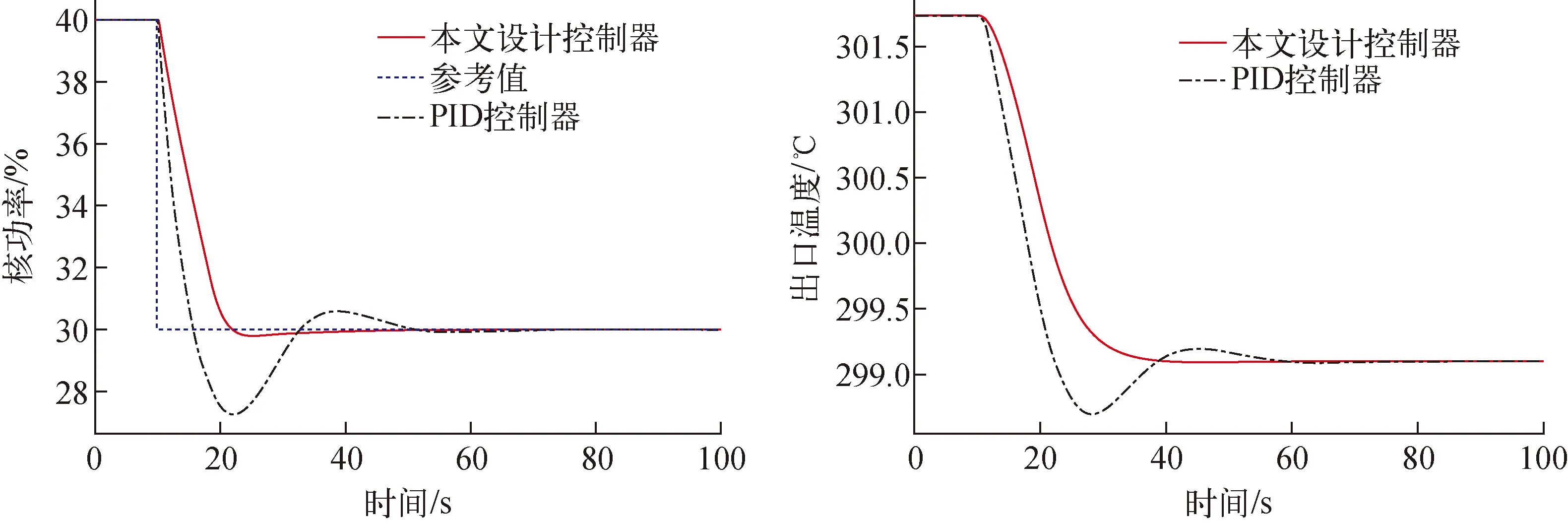
图7 40%FP-30%FP阶跃负荷仿真结果Fig.7 40%FP-30%FP step load simulation results

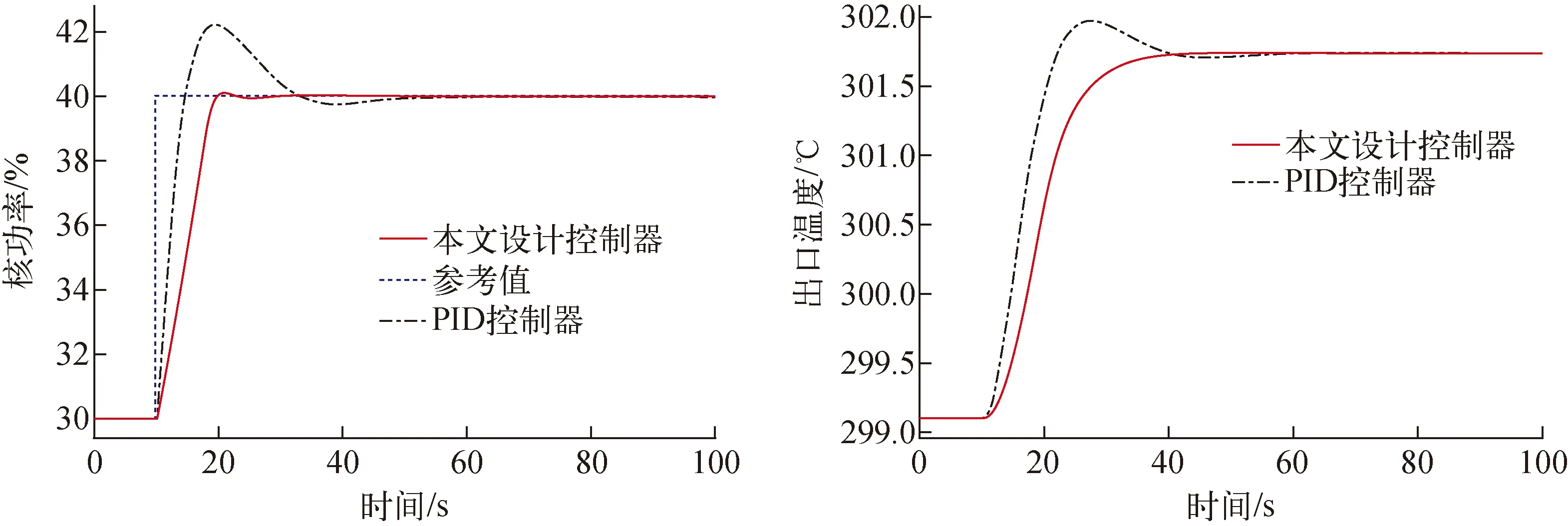
图8 30%FP-40%FP阶跃负荷仿真结果Fig.8 30%FP-40%FP step load simulation results

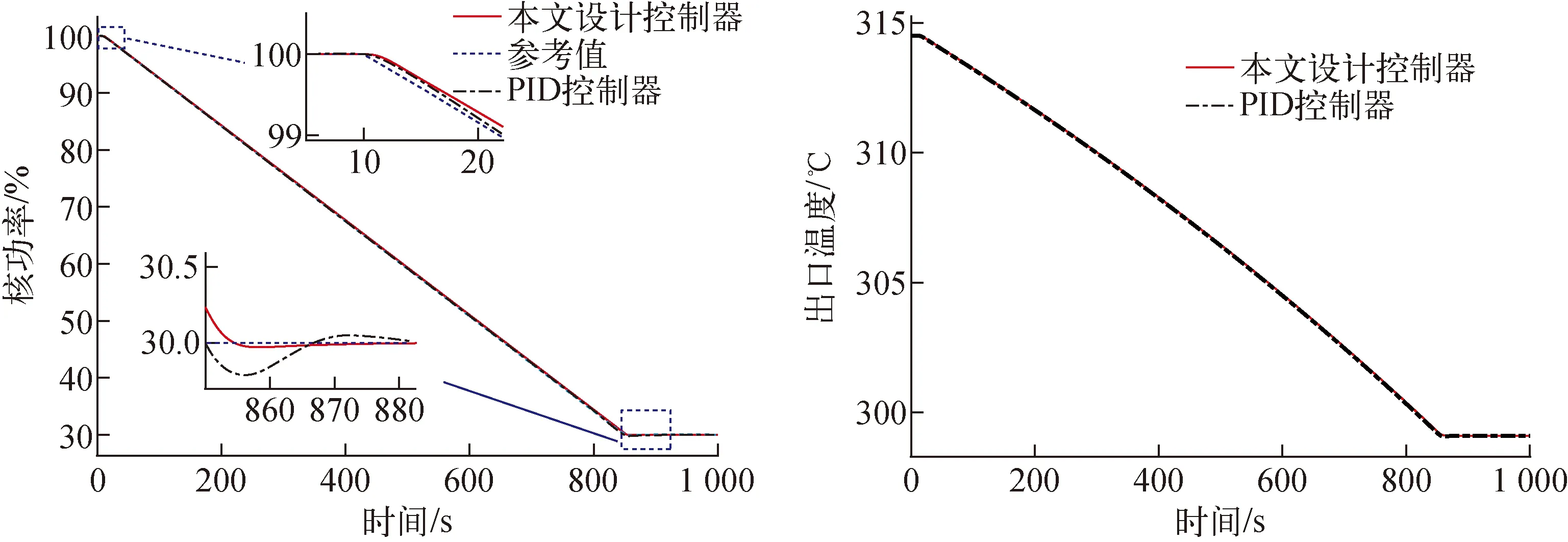
图9 100%FP-30%FP/-5%FP/min线性负荷仿真结果Fig.9 100%FP-30%FP/-5%FP/min linear load simulation results

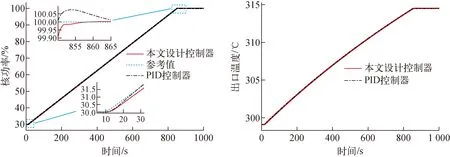
图10 30%FP-100%FP/+5%FP/min线性负荷仿真结果Fig.10 30%FP-100%FP/+5%FP/min linear load simulation results

从图9、10可看出，本文设计的LQG控制器对±5%FP/min的线性变负荷工况具有很好的控制性能，堆芯功率能快速准确地跟随参考功率的变化过程，超调量很小，且最后都能使堆芯功率稳定在参考值附近，稳态误差可忽略。同时，堆芯出口温度也随着堆芯功率的变化，最终稳定在新的稳态水平上。表明了本文设计的LQG堆芯功率控制器对±5%FP/min的线性变负荷工况具有优越的控制性能，能满足线性升降负荷的控制需求，且鲁棒性好。

从图5～10可看出，本文设计的LQG控制器以及传统的PID控制器在上述工况下都可以实现反应堆功率的控制，且具有良好的控制性能，但本文设计的经优化权重系数的LQG控制器的堆芯功率控制性能明显比PID控制器更优越，本文设计的LQG控制器的功率调节速度更快，超调量更小，控制性能更好。

4 结论

本文基于点堆模型推导了的反应堆堆芯状态空间模型；通过LQG方法，设计了反应堆功率控制系统的控制器；基于NSGA-Ⅱ算法，对LQG控制器的LQR权重系数进行了优化设计；在相同初始条件下，与PID控制器仿真对比了阶跃负荷工况、线性负荷变化工况，验证了本文提出的LQG控制器的在不同功率水平、不同瞬态工况下的控制性能和鲁棒性。本文结果表明，与传统PID控制器相比，基于NSGA-Ⅱ算法优化的LQG控制器不仅控制精度高，而且响应快速，稳定性好，稳态误差小，同时具有很好的鲁棒性，能满足反应堆功率控制的要求，具有较好的研究意义和应用前景。