改进的非线性RMPSVM及TMPSVM

代永潇，李晓萌，范丽亚

(聊城大学 数学科学学院，山东 聊城 252059)

0 引言

支持向量机(Support Vector Machine，SVM)[1]自Vapnik等人[2]于1995年提出后得到了大量的改进和应用，如最小二乘SVM(Least Squares SVM，LSSVM)[3]，孪生SVM(Twin SVM，TSVM))[4]，孪生有界SVM (Twin Bounded SVM，TBSVM)[5]，拉普拉斯TSVM(Laplacian SVM，Lap-TSVM)[6]，鲁棒TSVM(Robust SVM，RTSVM)[7]等。不同于SVM，TSVM是通过求解一对较小尺寸的二次规划模型(Quadratic Programming Problem，QPP)，得到两个非平行超平面进行分类。

最小最大概率机(Minimax Probability Machine，MPM)是Lanckriet等人[8]于2001年提出的一类分类器，其基本思想是所寻找的分类超平面使得正负样本分列超平面两侧的最小概率越大越好。 近年来，MPM得到了诸多改进，如拉普拉斯MPM(Laplacian MPM，Lap-MPM)[9]，最小误差MPM(Minimum Error MPM，MEMPM)[10]等，同时也得到了越来越广泛的应用[11-13]。 2015年，Xu等人[14]结合MPM和TSVM思想，提出了一种孪生最小最大概率机(Twin MPM，TMPM)；2019年，Yang等人[15]结合MPM和终端学习机(Extreme Learning Machine，ELM)思想，提出了最小最大概率ELM框架(Minimax Probability ELM Framework，MPELMF)；2020年，Ma等人[16]结合MPM和孪生终端学习机(Twin ELM，TELM)，提出了孪生最小最大概率终端学习机(Twin Minimax Probability ELM，TMPELM)；同年，Yang等人[17]结合MPM和TSVM思想，提出了无分布贝叶斯分类器，称为孪生最小最大概率机(Twin Minimax Probability Machine，TMPM)。

受上述研究启发，本文提出了非线性的改进MPM(Improved MPM，I-MPM)，结合非线性I-MPM和非线性SVM思想，提出了两个新的分类算法：一是非线性正则化最小最大概率SVM(Regularized Minimax Probability SVM，RMPSVM)，另一是改进的非线性孪生最小最大概率SVM(Improved Twin Minimax Probability Support Vector Machine，I-TMPSVM)算法。前一个算法解决了矩阵的奇异性问题，后一个算法利用多元切比雪夫不等式和适当变换，建立了非线性I-TMPSVM的一对较小尺寸的凸二次规划原始模型，从而保证了算法具有全局最优解，并能简单有效求解。非线性I-NTMPSVM不仅考虑了数据的几何信息，还考虑了数据的均值和协方差。实验结果表明，本文所提的非线性I-TMPSVM的计算复杂度优于非线性TSVM，同时还具有非线性TSVM和非线性I-MPM的优势。

1 预备知识

本节简要回顾非线性SVM、TSVM及两种MPM和TSVM结合的分类算法，详细内容见文献[1，2，4，15，16]。

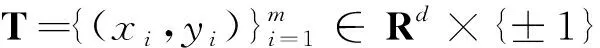
1.1 非线性软间隔支持向量机(C-SVM)

非线性C-SVM[1-2]是通过二次规划模型

(1)

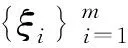
(2)

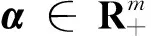
算法1(非线性C-SVM)

步2选择适当的核函数k:Rd×Rd→R和核参数。

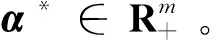
步4计算系数向量β*=Dα*。

步6构造分类决策函数f(x)=Kxβ*+b*=[k(x，x1)，…，k(x，xm)]β*+b*。

1.2 非线性孪生支持向量机(TSVM)

不同于非线性C-SVM，非线性TSVM[8]是通过下面一对较小尺寸的二次规划模型

(3)

来寻找两个分类超曲面

f1(x)=+b1=0，f2(x)=+b2=0，

式中c1，c2>0为模型参数，w1，w2∈H和b1，b2∈R分别是超曲面的法向量和阈值。

由于H=span{φ(x1)，…，φ(xm)}，存在系数向量β1，β2∈Rm使得w1=φ(X)β1，w2=φ(X)β2。 于是，模型(3)可表示为关于系数向量的形式

(4)

(5)

分别考虑模型(4)和模型(5)的Lagranre函数

并令∂L1/∂β1=∂L1/∂b1=∂L1/∂ξ=0和∂L2/∂β2=∂L2/∂b2=∂L2/∂η=0，可得

GGTu1=-Hα，HHTu2=Gβ，

式中

不失一般性，设GGT和HHT是非奇异阵(否则，将其正则化)。模型(4)和(5)的Wolfe对偶形式分别为

(6)

(7)

算法2(非线性TSVM)

步2选择适当的核函数k:Rd×Rd→R和核参数。

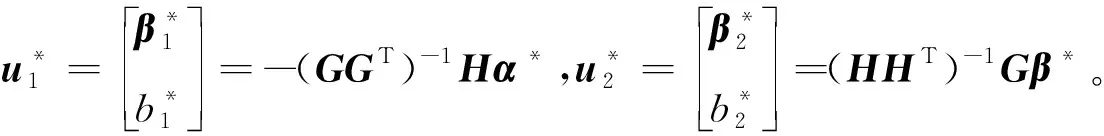
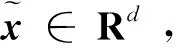
1.3 最小最大概率机(MPM)

线性MPM[5]是通过求解优化模型

(8)

来寻找分类决策函数f(x)=-b的，其中α∈(0，1)，w∈H和b∈R分别是决策函数的法向量和阈值，<·，·>表示内积。利用Chebyshev-Cantelli不等式，模型(8)可转化为二阶锥规划(Second Order Cone Programming，SOCP)模型

(9)

模型(9)可利用SeDuM[18]内点算法进行求解。

1.4 MPM和TSVM的结合算法

本节简要介绍一种MPM和TSVM结合的分类算法，即线性TMPM。

线性TMPM[21]是通过求解下面一对优化模型

(10)

(11)

来寻找分类决策函数f1(x)=-b1-1，f2(x)=-b2+1。模型(10)和模型(11)可分别转化为具有非仿射分母的凹分数规划模型

(12)

(13)

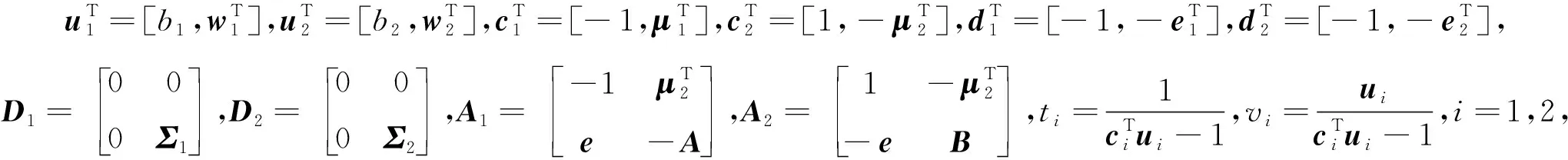
则

(14)

于是，模型(12)和模型(13)可转化为凸二次规划模型

(15)

(16)

算法3(线性TMPM)

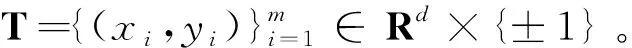
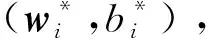
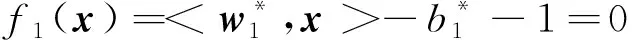
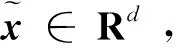
线性TMPM的不足在于只考虑了异类样本尽可能远的情况下，最大限度地降低同类样本最坏情况(最大)下的错分概率，而没有考虑同类样本尽可能近。

2 改进的MPM (Improved MPM，I-MPM)

非线性I-MPM的基本思想是在特征空间H中寻找分类超曲面f(x)=wTφ(x)+b=0，使得两个随机向量的样本取值分列超平面两侧的最小概率(用概率的下确界表示)越大越好，其中w∈H，b∈R分别是决策函数的法向量和阈值。可用如下优化模型表示

(17)

式中α∈(0，1)。根据引理1和推论1，模型(17)可等价地转化为

(18)

由于H=span{φ(x1)，…，φ(xm)}且w∈H，存在系数向量β=[β1，…，βm]T∈Rm，使得

w=β1φ(x1)+…+βmφ(xm)=φ(X)β。

(19)

于是，分类决策函数和模型(18)可分别转化为关于系数向量的形式f(x)=Kxβ+b和

(20)

记G=K(A，X)，H=K(B，X)，h=[1，-1]T，q=[0，1]T，r=[1，0]T，u=[α，γ]T∈R2，并考虑模型(20)的Lagrange函数

且令∂L/∂β=∂L/∂b=0，可得

式中α=α1=α2，得

(21)

式中t>0为正则化参数，根据模型(20)的约束条件，可取

(22)

于是，模型(20)的Wolfe对偶形式为

(23)

下面给出具体算法。

算法4(非线性I-MPM)

步2选择适当的核函数k:Rd×Rd→R和核参数。

步3计算均值向量(μ1，μ2)和协方差矩阵(Σ1，Σ2)。

步4求解模型(23)，得最优解u*∈R2。

步5求解(21)式求解系数向量β*∈Rm，其中u=u*。

步6求解(22)式计算阈值b*∈R，其中u=u*。

步7构造分类决策函数f(x)=Kxβ*+b*=0。

3 改进的TMPSVM (Improved TMPSVM，I-TMPSVM)

本节首先提出一种全新正则化最小最大概率SVM(Regularized Minimax Probability SVM，RMPSVM)算法，其次利用SVM思想对第2节提出的I-MPM与TSVM结合算法进行改进，并讨论非线性情况。

3.1 非线性正则化MPSVM (RMPSVM)

非线性RMPSVM的基本思想是在特征空间H中寻找一对间隔尽可能大的平行边界超平面+b=1和+b=-1，使得两类样本分列其两侧的最小概率越大越好，中间者为分类超曲面f(x)=+b=0。为此，建立如下优化模型

(24)

式中α∈(0，1)，C>0是调节参数，ξ=(ξ1，…，ξm)T∈Rm是松弛向量。 由于

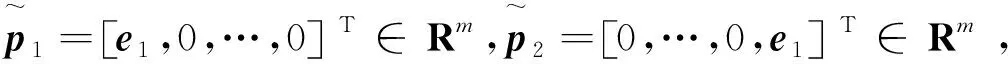
(25)

式中e=[e1，e2]T∈Rm。由于H=span{φ(x1)，…，φ(xm)}且w∈H，存在系数向量β=[β1，…，βm]T∈Rm，使得w=φ(X)β。于是，分类超曲面和模型(25)可分别转化为系数向量的形式f(x)=Kxβ+b=0和

(26)

式中G，H，P1，P2同第2节。记

并考虑模型(26)的Lagrange函数

且令∂L/∂β=∂L/∂b=∂L/∂ξ=0，可得

(27)

将(31)式代入Lagrange函数中，可得模型(30)的Wolfe对偶形式

(28)

下面给出具体算法。

算法5(非线性RMPSVM)

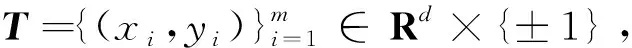
步2选择适当的核函数k:Rd×Rd→R和核参数。

步3计算均值向量(μ1，μ2)，协方差矩阵(Σ1，Σ2)和矩阵Q，P。

步4求解模型(28)，得最优解u*∈R3。

步5利用(27)式计算β*∈Rd和b*∈R，其中u=u*。

步6构造分类超曲面f(x)=Kxβ*+b*=0。

3.2 改进的TMPSVM (I-TMPSVM)

不同于1.4节中提出的MPM和TSVM结合的分类算法，本节提出的非线性I-TMPSVM的基本思想是在特征空间H中寻找一对非平行超曲面f1(x)=+b1=0和f2(x)=+b2=0，使得两类样本分列其两侧的最小概率越大越好，同时又满足距离一类数据尽可能近。为此，建立下面一对优化模型

(29)

(30)

式中α，β∈(0，1)，c1，c2>0是调节参数。由引理1和推论1，模型(29)和模型(30)可等价地转化为

(31)

(32)

式中ξ∈Rm2，η∈Rm1。由于H=span{φ(x1)，…，φ(xm)}且w1，w2∈H，存在系数向量

β1=[β11，…，β1m]T，β2=[β21，…，β2m]T∈Rm，

使得w1=φ(X)β1，w2=φ(X)β2。于是，两个非平行超曲面及模型(31)和模型(32)可分别表示为系数向量形式f1(x)=Kxβ1+b1=0，f2(x)=Kxβ2+b2=0，和

(33)

(34)

式中G，H，P1，P2同第2节。记

并分别考虑模型(33)和模型(34)的Lagrange函数

及令∂L1/∂β1=∂L1/∂b1=∂L1/∂ξ=0，∂L2/∂β2=∂L2/∂b2=∂L2/∂η=0，可得

(35)

式中t>0是正则化参数。模型(33)和模型(34)的Wolfe对偶形式分别为

(36)

(37)

下面给出具体算法。

算法6(非线性I-TMPSVM)

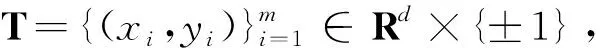
步2选择适当的核函数k:Rd×Rd→R和核参数。

步3计算均值向量(μ1，μ2)，协方差矩阵(Σ1，Σ2)和矩阵M，N。

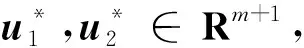
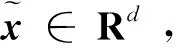
4 实验与结果分析

本节利用UCI数据库中的8个数据集(任选14个二分类数据集)对本文提出的三个非线性算法与非线性SVM，TSVM进行对比实验，实验结果见表1和表2，其中xx，m和t分别表示训练样本数、样本总数和运行时间，ACC，σ和C分别表示分类精度、核参数和模型参数。 采用五折交叉验证法，所用参数在10-2～102范围内采用网格搜索寻优。为直观起见，提供了部分分类精度和运行时间的对比柱状图。

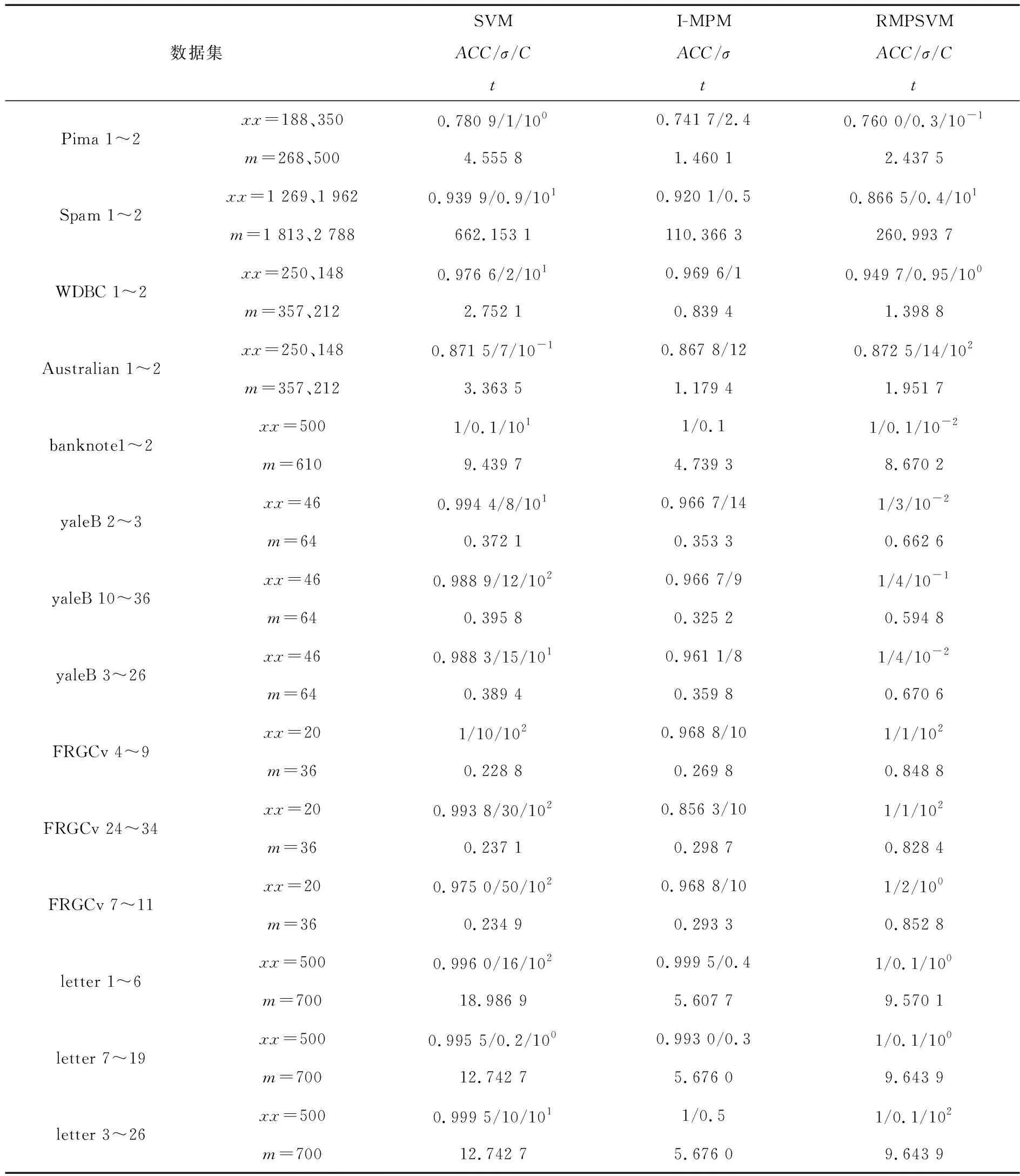
表1 非线性SVM，I-MPM与RMPSVM的对比实验结果

从表1中可以看出，本文提出的非线性I-MPM和非线性RMPSVM算法在分类精度上不弱于非线性SVM，但在运行时间上少于非线性SVM，尤其是非线性RMPSVM在8个二分类数据集上的分类精度达到了100%。与非线性I-MPM相比，非线性RMPSVM在分类精度上优于非线性I-MPM，但在运行时间上比非线性I-MPM略长。从表2中可以看出，本文提出的非线性I-TMPSVM算法在6个数据集上的分类精度达到了100%，在7个数据集上的精度优于非线性TSVM，并且运行时间更少。与非线性I-MPM相比，非线性I-TMPSVM在14个数据集上的精度上优于非线性I-MPM，运行时间差别不大。

综上所述，本文提出的非线性I-MPM和非线性RMPSVM算法总体上优于非线性SVM，所提的非线性I-TMPSVM算法不仅具有较低的计算复杂性，而且分类性能优于非线性TSVM和非线性I-MPM算法。

表2 非线性TSVM，I-MPM与I-TMPSVM的对比实验结果

5 结束语

本文利用二次规划的Wolfe对偶形式改进了传统的非线性MPM，并提出了两种新的分类算法，非线性RMPSVM和非线性I-TMPSVM。 非线性I-TMPSVM不仅使两类样本分列两个超曲面两侧的最小概率越大越好，同时还满足一个超曲面距离一类数据尽可能近，排斥另一类数据尽可能远，具备了非线性TSVM和非线性I-MPM的优势，提高了非线性I-MPM的分类准确性。实验结果表明，非线性RMPSVM在分类精度上优于非线性I-MPM，非线性I-TMPSVM计算复杂度低，泛化能力优于非线性I-MPM和非线性TSVM，而且可以通过极小化错分最大概率来直接估计概率精度界，此外，非线性I-TMPSVM的运行时间也少于非线性TSVM。虽然非线性I-TMPSVM与非线性I-MPM相比分类准确性高，但总体运行时间差别不大，因此，本文的后续工作是在所提算法的基础上，进一步考虑与其他形式的非线性SVM和非线性TSVM结合，以期提高非线性SVM和非线性TSVM的分类性能，泛化能力以及运行时间。

图1 部分实验结果对比柱状图