两类大跨钢波纹管涵洞力学特性对比分析

祝海默，阙 云，谷 音

(福州大学 土木工程学院，福建 福州 350108)

我国在建国初期开始钢波纹管涵洞的应用，但直到20世纪90年代末期，钢波纹管涵洞才逐渐开始发展，至今推广应用涵洞超过1 500道[1]，特别在青海、西藏、内蒙古、上海、新疆等地，有较大规模应用。在我国公路桥涵发展背景下，钢波纹管涵洞造价低、环保、施工简单等诸多优点使其具有相当大发展前景，具有较高研究价值。

近年来国内外研究人员从几个方面对钢波纹管涵洞进行了研究。(1)管涵力学性能方面：杨松等[2]通过数值模拟研究表明2.5 m管径钢波纹管能满足1 m～5 m填土要求；田子瀚[3]通过室内HDPE波纹管平行板加载试验，研究了不同类型HDPE波纹管的受力变形特性及环刚度对波纹管性能的影响；Regier等[4]对具有不同腐蚀程度和两侧土壤覆盖层的涵洞进行了一系列试验，结果表明大多数劣化程度下，回填压实对劣化管道影响比腐蚀更大；Tehrani[5]采用室内试验的方法，通过施加垂直静荷载来评估钢波纹管涵洞结构承载力，结果表明:圆形钢波纹管涵承载力取决于其环向刚度，而拱形钢波纹管利用了拱的几何结构，能够抵抗施加的荷载。(2)涵周土压力方面：刘辉民等[6]对10 m孔径钢波纹管的土压力进行研究，表明现行规范过于保守；魏瑞等[7]以顾安全公式和Spangler管涵相互作用模型为基础，推导了钢波纹管涵洞涵顶垂直土压力计算公式并加以验证；朱健[8]对软土地基上高填方涵洞的土压力进行分析，推导了计算涵洞“中性点”位置的理论公式，并结合数值模拟分析，研究了对“中性点”的影响因素。(3)涵洞减荷措施方面：魏瑞等[9]对高填方大直径钢波纹管进行了减荷试验研究，表明EPS板具有显著减荷效果与调节土压力分布作用；Sun等[10]进行了涵洞减荷现场试验，试验涵洞为钢筋混凝土箱涵，试验结果表明，EPS板减荷效果明显，埋设有EPS板的断面涵顶垂直土压力，仅为没有埋设EPS板的28%；Simpson B等[11]通过在现有涵洞内插入新管道来减小荷载；Mahgoub等[12]通过在涵洞上方安装可压缩材料TDA来降低涵周土压力进行减荷，并对参数进行了深入研究，结果表明该方式可以有效降低涵洞应力和变形。

以上研究虽解决了钢波纹管涵力学方面多类问题，但研究对象及研究成果主要集中在小孔径(管径<4 m)管涵。随着钢材可塑性的提高及应用，以及公路桥涵的发展对于涵洞跨径的需要，大跨径钢波纹管涵洞成为今后发展趋势，我国研究人员对钢波纹管涵的研究也逐步转向该类管涵。

另外，现有研究基本停留在圆形管涵结构(以下简称圆涵)，对于近年发展下衍生的新型钢波纹管-混凝土组合式拱涵(以下简称拱涵)研究较少。因此，本文以承德利基国道112线庙岭涵洞项目为依托，采用有限元技术，分别对圆涵和拱涵的力学性能进行了研究。此外，大跨径钢波纹管涵通常采用某项减荷措施以提高结构安全性，本文对采取EPS板减荷后两种结构涵洞进行了进一步对比研究。

1 工程概况

以承德利基国道112线庙岭涵洞项目实际工程为依托，设计采用钢波纹管参数、波纹大样分别如表1和图1。其中，波纹管参数中截面模量为截面对其形心轴惯性矩与截面上最远点至形心轴距离的比值，用于计算截面受弯时正应力的大小。

设计采用拱涵，跨径12 m，矢高6 m，与混凝土基础通过高强螺栓连接，中间设有路面结构层，如图2(a)。为对比两类涵洞，构造圆涵相同孔径，通过开挖地基置换土体在底部铺设砂石垫层，管涵底部铺设级配碎石，如图2(b)。

表1 截面特性

图1 波纹大样(单位：mm)

2 数值模拟

2.1 计算模型

确保有限元模型精度的两大主要因素分别为本构模型与计算参数。根据文献[13]，金属塑性问题应采用Von Mises屈服准则，填土与地基土应采用Mohr-Coulomb屈服准则。

模型选用单元如下：钢波纹管选用一般壳单元，S4R；土体选用三维实体单元，C3D8R，本构为摩尔-库仑[14-17]。边界条件为：地基底全固定，两侧土体限制X向平动，管轴向土体对称约束Z向平动，X向及Y向转动[18]。管土接触由于施工时分层填土，充分压实，为考虑这一点，建模时采用Model Change功能，将土体分层填筑[19]，材料选用如表2。

根据圣维南原理，可以取部分结构计算，取管轴向长度取4个波长(1.52 m)，结构立体网格如图3。

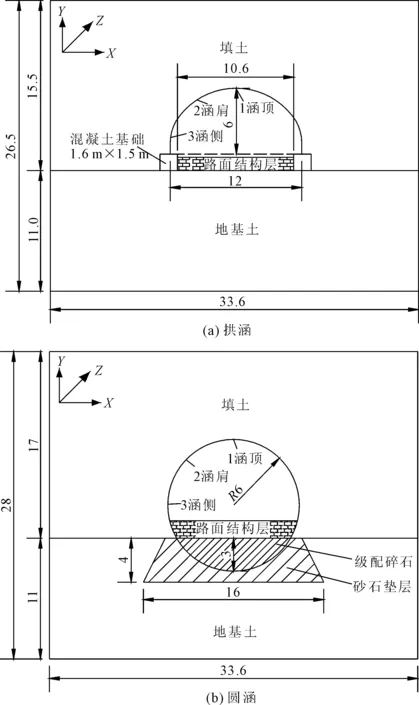
图2 两类涵洞尺寸(单位：m)

表2 材料参数

2.2 计算精度验证

依托湖南省龙永高速公路K64+292刚波纹管涵工程实测数据，采取相同建模方式，验证本模型的可靠性。

该工程管涵管径为5.0 m，波形200 mm×55 mm(波长×波高)，板厚7 mm，管顶填土高度17.9 m，管身长81.67 m[10]。

应变测试元件采用表贴式智能弦式数码应变计，测试仪器为便携式智能型多功能测试仪；变形测试采用全站仪测试；土压力测试采用埋入式智能弦式土压力传感器，测点布置如图4所示。

图3 立体结构网格

图4 测试截面测点布置

模型尺寸选取如下：宽19 m，长0.8 m(4个波长)，基础为80 cm厚级配砂砾，垫层为15 cm厚粗砂，填土高度相同，波形、壁厚、管径与实际波纹管相同。模型所用材料参数如表2。

采用分层填土方式，表3和图5为填土至管顶与管顶填土高度最大(17.9 m)时部分计算结果与土压力对比情况。表中符号含义为：竖向变形下“﹢”、上“﹣”，水平变形右“﹢”、左“﹣”，拉压力拉“﹢”、压“﹣”[10]。

表3 部分试验结果与计算结果

图5 径向土压力对比

3 结果分析

3.1 不同填土高度的影响

图6—图9分别为两类涵洞结构垂直土压力、等效应力、水平变形、竖向变形在不同填土高度下分布规律，其中图7—图9为管涵接近屈服时填土高度下波纹管云图。

由图6—图9可见：

(1) 两种结构垂直土压力均呈“中间小两侧大”分布，原因是受“土拱效应”影响，填土越高影响越大，且拱涵更明显，说明拱涵卸荷更优。

(2) 两种结构内力、竖向变形、水平变形分布规律差距不大，圆涵上半部基本等于拱涵，最不利点位置相同，分别位于涵侧、涵顶、涵侧。

(3) 根据文献[20]，管涵最终变形量应小于设计形状2%，最大等效应力应小于屈服应力。在接近屈服时，两种结构变形均远小于限值，因此，建议以最大等效应力控制设计。

图6 垂直土压力分布

图7 两种结构等效应力云图(单位：Pa)

图8 两种结构水平变形云图(单位：mm)

图9 两种结构竖向变形云图(单位：mm)

图10为两种结构垂直土压力、最大等效应力、最大变形随填土高度增加变化曲线，最大填土高度14 m时管涵接近屈服。

由图10可见：

图10 两种结构受力变形对比

(1) 拱涵、圆涵两种结构涵顶垂直土压力均随涵顶填土高度增加线性增加，斜率分别为11.9、13.0，拱涵低8.5%。

(2) 两种结构最大等效应力均随涵顶填土高度增加线性增加，斜率分别为19.5、15.1，圆涵低22.6%。以钢波纹管屈服应力为235 MPa，圆涵、拱涵最大填土高度分别为12.0 m、10.6 m，圆涵高11.7%。

(3) 两种结构最大竖向变形与最大水平变形随涵顶填土高度增加线性增加。两种结构最大水平变形/最大竖向变形斜率分别为1.6/1.8、1.8/2.6，拱涵分别低11.1%、30.8%。

综上，两种结构垂直土压力、最大等效应力、最大水平、竖直变形均随填土高度线性变化。拱涵上方“土拱效应”更明显，卸荷更优，属于几何构造优势，但最大等效应力更大，承载力更低，且变形更小。原因在于，钢波纹管涵受力特征是通过自身柔性协调变形转移外荷载至周围土体，拱涵仅有一半钢波纹管发挥作用。此外，拱涵刚性基础增加了结构整体刚度。

3.2 控制点对比

为深入对比两种结构在力学特征上的差异，取结构具有代表性3个控制点，涵顶、涵肩、涵侧(图2)进一步对比，结果如图11。

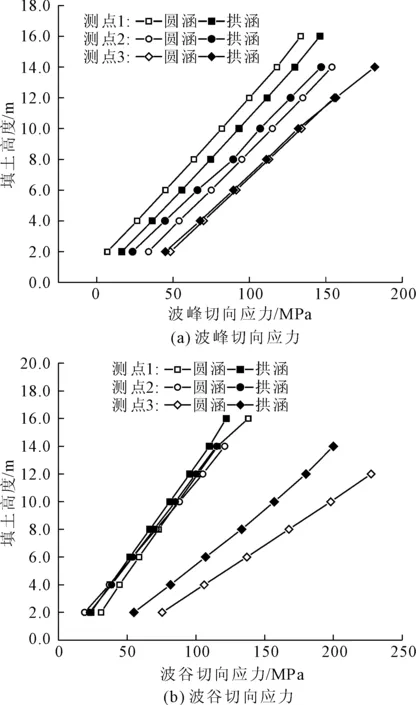
图11 控制点切向应力对比

由图11可见：

(1) 两种结构波峰、波谷切向应力均随填土高度增加线性增加。两种结构波峰应力斜率基本相同，波谷应力测点1与测点2基本相同，测点3圆涵大20.4%。

(2) 两种结构波峰、波谷切向应力大小依次为测点3、测点2、测点1，最大切向应力均在测点3波谷处。

说明两种结构波纹管内力、土压力传递规律基本相同：两类涵洞结构管涵协调变形使土压力由中心向两侧传递，由管涵向管周土体传递；波纹管内力由波峰向波谷传递。在测点3波谷切向应力存在较大差别，原因在于圆涵波峰挤压变形将力传到波谷，使其内力增大；而拱涵该点靠近基础限制波峰变形，波峰将部分力传递至基础，导致测点3土压力较大、变形较大。

3.3 EPS板减荷对比

3.3.1 EPS板减荷机理

传统涵洞，如钢筋混凝土、圬工砌体等涵洞与两侧、顶部填土相比，可视为刚性涵洞，具有较大刚性[21]。在填土压密回填过程中，涵顶平面填土沉降小于涵侧填土沉降，这种沉降差将会使位于两侧外土柱对位于中间内土柱形成向下附加摩擦力，从而使得涵顶产生附加垂直土压力，故涵顶填土压力可视为土柱压力与附加垂直土压力之和。

因此，要实现涵顶土压力减荷，就必须采取措施使附加垂直土压力减小，即沉降差δ减小，甚至产生一种向上有助于卸荷的摩擦力，即使外土柱沉降小于内土柱沉降，即产生沉降差-δ[21-23]。在涵顶铺设具有一定抗压强度的高压缩性材料，如EPS板，能在填土过程中提供一定压缩变形增量-△δ从而帮助结构减小沉降差δ，甚至产生反沉降差-δ来达到减小涵顶垂直土压力的目的，如图12所示为铺设与未铺设EPS板涵-土相互作用示意[24]。

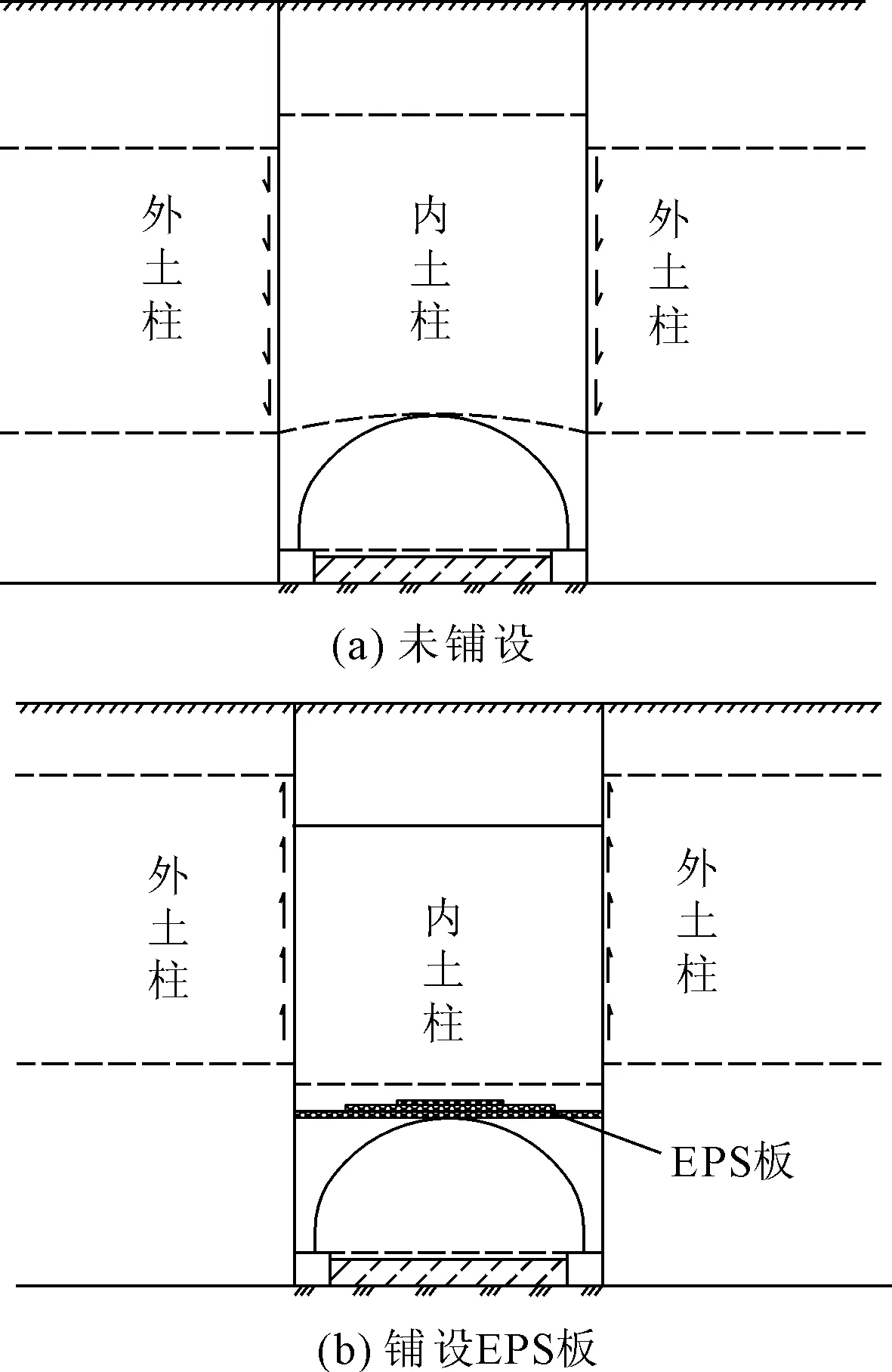
图12 涵-土相互作用[21](以拱涵为例)

3.3.2 EPS板本构模型

EPS板本构选用Crushable Foam模型，该模型是以土的双屈服面本构模型为基础发展而成，主要用来模拟泡沫材料压缩变形行为，参数依据以往研究选取[23-24]，如表4所示。

表4 EPS板参数

该本构模型不仅可以模拟EPS板的弹塑性变形，还能模拟EPS板的压缩硬化，适合模拟EPS板的受力变形行为，EPS板应力-应变曲线如图13所示，分为线弹性(OA)、塑性(AB)和硬化(BC)3个阶段，线弹性阶段应变约小于5%，此应变被看作材料的屈服点，EPS板材料应变为10%时所对应的应力被定义为抗压强度，此后材料进入塑性变形阶段，当应变达到60%时，材料开始进入硬化阶段[25]。

图13 EPS材料应力-应变关系曲线

3.3.3 涵顶垂直土压力

引入垂直土压力系数Kv来表示涵顶垂直土压力减荷状况，Kv表达式如下：

(1)

式中:σv为垂直土压力，kPa；γ为填土重度，kg/m3；H为填土高度，m。若Kv<1，则表明涵顶垂直土压力小于土柱重力，此时减荷；若Kv>1，则表明涵顶垂直土压力大于土柱重力，此时未减荷。

本节用3种EPS板厚度进行对比，计算结果如图14。

由图14可见：

(1)拱涵、圆涵两种结构垂直土压力系数在未铺设EPS板、铺设80cm厚度EPS板下分别为0.658、0.715；0.373、0.394，均降低43%左右。

(2)铺设EPS板后两种结构涵顶垂直土压力随填高增加由线性增加变为增幅逐渐减小的非线性增加；当EPS板厚超过30 cm，增加板厚影响不大；当涵顶填土高度与管径比值，即H/D>2/3后，减荷效果明显加强。

综上，铺设EPS板后，垂直土压力减小且变为非线性变化；在H/D>2/3后EPS板作用明显加强且在EPS板厚度大于30 cm后增加板厚对土压力影响不大，两种结构减荷效果基本相同。

图14 涵顶垂直土压力对比

3.3.4 最大等效应力

采用结构最大等效应力反映EPS板减荷对于管涵结构的影响。计算结果如图15所示。

图15 管涵最大等效应力变化

由图15可见：

(1) 拱涵、圆涵两种结构铺设EPS板后最大等效应力均降低并且随填高增加均变为非线性增加。拱涵降低幅度更大，同一填高下，两类涵洞结构最大等效应力变为拱涵更小。

(2) 以铺设80 cm EPS板为例，拱涵、圆涵两类涵洞结构上覆最大填土高度分别增加81.1%、47.5%，拱涵增加更大。

综上，铺设EPS板两种结构最大等效应力均降低且变为非线性变化，拱涵波纹管内力降幅更大、上覆最大填土高度增大更大。

4 结 论

(1) 受“土拱效应”影响，两类涵洞结构垂直土压力均呈“中间小两侧大”分布，但拱涵影响更大、卸荷更优，且高填土下更明显；两类涵洞结构力学分布规律基本相同，最不利点均位于涵侧及涵顶；两类涵洞结构均是波纹管内力较变形增长快，建议作为设计控制指标。

(2) 两类涵洞结构土压力传递规律相同，即由中心向两侧、管涵向管周土体传递；波纹管内力传递规律相同，即由波峰向波谷传递，但拱涵涵侧处波峰将部分内力传递至基础，故该点波谷应力较小。

(3) 两类涵洞结构垂直土压力、最大等效应力均随填土高度增加线性增加，铺设EPS板后均减小，且变为非线性增加；在EPS板厚30 cm后增加厚度对土压力、结构等效应力影响均不大且当H/D>2/3后EPS板作用更明显。

(4) 两类涵洞结构垂直土压力减荷效果相同、但拱涵波纹管内力减小更多，上覆最大填土高度更大。综上，大跨拱涵力学性能与EPS板卸荷效果均优于大跨圆涵。