BEC上基于内插算法的多元SC-LDPC码BP译码波速度分析*
许梦楠,吴雅婷,施文明,张钟浩
(上海大学 a.上海先进通信与数据科学研究院;b.特种光纤与光接入网重点实验室;c.特种光纤与先进通信国际合作联合实验室,上海 200444)
0 引 言
空间耦合低密度奇偶校验(Spatially-Coupled Low-Density Parity-Check,SC-LDPC)码[1]在置信传播(Belief Propagation,BP)译码[2]下具有比底层码更优异的性能[3]。SC-LDPC码的消息在耦合链的两端产生,随着迭代次数的增加,消息沿着耦合链向中间传播,这就是SC-LDPC码的译码波传播[4]。多元LDPC码定义在有限域GF(2m)上,m表示每符号含有的比特数[5]。SC-LDPC码相比LDPC码存在阈值饱和现象,即BP阈值饱和于最大后验(Maximum A Posteriori,MAP)阈值[6-7]。已经证明二元SC-LDPC码在二进制擦除信道(Binary Erasure Channel,BEC)上存在阈值饱和现象[8]。对于多元SC-LDPC码,可以借助势函数证明在BEC上阈值饱和[9]。
近些年来,译码波的速度分析引起了人们的广泛关注:文献[8]指出译码波速度会随着迭代次数的增加而收敛;文献[10]利用度分布和非耦合密度演进(Density Evolution,DE)递归式的不动点(Fixed Point,FP)可以计算译码波速度的临界点;文献[11]推导了译码波速度的表达式并推广到一般的空间耦合系统;文献[12]提出了插值密度演进算法,利用此算法分析了二进制无记忆对称信道(Binary Memoryless Symmetric Channel,BMSC)上二元SC-LDPC码译码波的速度。
本文运用内插密度演进(Density Evolution,DE)算法分析多元SC-LDPC码在BEC上BP译码波速度。通过观察译码波的密度演进发现,轮廓译码(Decoding Profile,DP)可以看作一条通过非耦合DE递归式的不动点的路径。受此启发,可以利用一维内插函数在非耦合DE递归式的FP间插值密度来近似表示DP,这样避免利用耦合DE递归式从而降低计算复杂度。在更新内插函数时,将变量节点(Variable Node,VN)和校验节点(Check Node,CN)间的转移函数进一步简化来降低计算复杂度。仿真和分析结果表明,在相同的度分布和信道条件下,与耦合DE算法相比,本文提出的内插DE算法在取得很好的性能同时降低了计算的复杂度。
1 耦合DE算法
1.1 符号和定义
多元LDPC码定义在有限域GF(2m)上,m表示每符号含有的比特数[4],其中λ和ρ分别表示变量节点和校验节点的边度分布。
多元SC-LDPC(λ,ρ,m,L,w)码,其中L和w分别表示耦合长度和宽度。SC-LDPC码的构造:首先将单个LDPC码的原模图复制L相同的副本,放置在位置{1,2,…,L},用整数k表示位置的索引;然后在位置k处,将变量节点的边均匀随机地分成w组,依次与位置为{k,k+1,…,k+w-1}的校验节点相连;同样地,将位置k处的校验节点的边均匀随机地分成w组,依次与位置为{k-w+1,k-w+2,…,k}的变量节点相连。
图1给出了耦合宽度w为3的SC-LDPC码的原模图构造过程。SC-LDPC码的结构导致了BP译码算法中译码波由耦合链的两端产生然后向中间传播。

图1 SC-LDPC码原模图构造过程
1.2 BP译码算法中消息密度
将在BEC上传输的消息分布称为密度,本文分析BP译码算法中多元SC-LDPC码的密度演进(Density Evolution,DE)。在BP译码算法中VN和CN间交换的消息是非负向量r=(r0,r1,…,ri),其中ri表示码字符号x为xi的后验概率。例如m=2,有四种可能的码字符号,即x0=00,x1=01,x2=10,x3=11,消息r=(0.25,0.25,0.25,0.25)表示P(x=00)、P(x=01)、P(x=10)和P(x=11)都为0.25。在BP译码算法中跟踪密度很困难,因为每个码字符号有2m种可能值。幸运的是,在BEC上,BP译码性能不依赖具体的传输码字,因此假如全为零的码字传输。这样在BEC上,消息等价于GF(2m)的一个子空间。跟踪密度转化为跟踪消息的维数。消息维数为k指的是有2k非零元素。基于此,密度演进简化为长度为m+1的消息交换。例如m=3,m+1维的消息向量a=(a0,a1,…,ai,…,am)=(1,0,0,0),0≤i≤m,i=0,a0=1指消息维度为0的概率为1,也就是消息译码发生0比特翻转的概率为1;同理,i=m,am=0指消息维度为m的概率为0,也就是消息译码发生m比特翻转的概率为0,表明码字符号可以无错地从传输的消息中译码。
定义1BEC上BP译码算法中多元SC-LDPC码的消息密度为长度为m+1的概率向量。定义密度集合
(1)
其中有两个极限密度,Δ0=(1,0,…,0,0)表示码字符号可以无错地从传输的消息中译码,Δm=(0,0,…,0,1)表示传输的消息没有为译码提供任何信息。
1.3 熵函数
定义2对于任意的a∈χ,a=(a0,a1,…,am),熵函数定义为
(2)
用熵函数来衡量消息的平均不确定度。
1.4 多元LDPC(λ,ρ,m)
定义3两个维度为m+1的概率向量a和b,
(3)
(4)
k∈{0,1,2,…,m},
(5)
(6)
高斯二项式系数
(7)
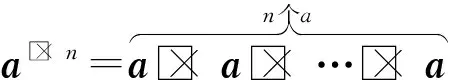

定义4多元LDPC(λ,ρ,m)在删除概率为ε的BEC上传输,第l轮迭代的非耦合DE递归式为
(8)
x(l)=p(ε)λ(ρ(□×x(l-1))),∀l>0。
(9)
式中:
λ(a)=∑iλia,
(10)
ρ□×(b)=∑jρjb□× j-1。
(11)
信道密度
(12)
特别地,当x(∞)=(1,0,…,0),表明成功译码。
定义5非耦合DE递归式(9)的不动点指的是密度对(x,y)满足y=ρ□×(x),x=p(ε)λ(y)。
对每个FP,总存在一个初始密度x(0),使非耦合DE递归式(9)收敛于这个FP。只要给定初始密度x(0)和信道密度p(ε),运行非耦合DE递归式(9)就可得到FP。用(x,y)=T非耦合DE(x(0),p(ε))表示FP。
定义6∃ε1,ε2,0≤ε1<ε2≤1,对非耦合DE递归式(9)的FP进行扰动擦除初始化:
(x,y)=T非耦合DE(εΔm+(1-ε)Δ0,p(ε)),∀ε∈[ε1,ε2]。
(13)
用S={(xi,yi)},i∈IS表示经过扰动擦除初始化的FP的集合,IS={0,1,…,NS-1}。经过扰动擦除初始化的FP是严格按照退化排列。分析发现,多元SC-LDPC码的译码波动态特性可以用非耦合DE递归式的稳定的FP来表征。本文提出的内插DE算法中,若FP按照严格的退化排列,则DP也具有单调性,所以本文提到的FP都是经过扰动擦除初始化的FP。
1.5 多元SC-LDPC(λ,ρ,m,L,w)的耦合DE算法
定义7多元SC-LDPC(λ,ρ,m,L,w)在删除概率ε的BEC上传输,第l轮迭代的耦合DE递归式为
(14)
(15)
1≤i≤L+w-1,
(16)
本文考虑L→∞和w→∞连续条件下的情形,对应的Tanner图,底层集成沿着耦合链以连续的方式放置,位置索引为连续的变量t∈R∪{±∞}。位置t处的变量节点的边均匀随机地连接到位置为[t,t+1)的校验节点;同样地,位置t处的校验节点的边均匀随机地连接到位置为(t-1,t]的变量节点。令t=i/w,式(14)转化为式(17):
(17)
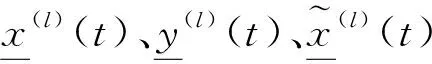
定义9将DP初始化:
(18)
这样有
(19)
2 非耦合DE递归式FP和DP
DP可以看作是沿着耦合链包含FP的密度路径。FP将DP分成一个或多个过渡区间,每个过渡区间有着自己的移动速度。下面重点讨论DP的动态特性并为内插DE算法的提出创造条件。
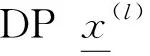
(20)

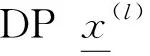
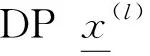
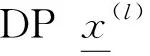
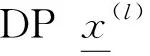
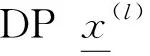
(21)

利用单个过渡区间移动速度的正负性可预测过渡区间的收敛性,例如两个相邻非跳动FP{x0,x1}构成的过渡区间τ1=τ(x0,x1,l),如果过渡区间的移动速度v1>0,那么DP将收敛于FPx0;如果v1<0,DP将收敛于FPx1。因此,BP阈值对应于v1=0。
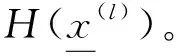
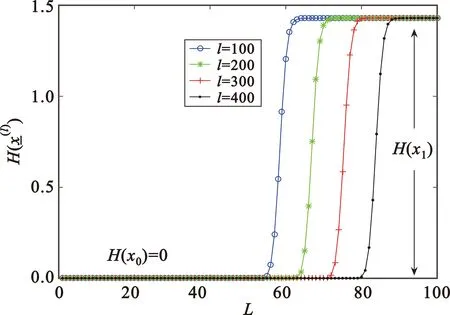
图2 采用耦合DE算法得到的熵函数

图3 采用内插DE算法得到的熵函数
3 内插DE算法
3.1 内插DE算法递归式

(22)
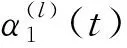
定义14内插DE算法中构造两个转移函数来更新内插函数,如公式(23)所示:
(23)
定义15第l轮迭代的内插DE递归式为
(24)
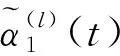
(25)
(26)
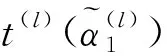
(27)
3.2 简化转移函数的计算
定义18本文讨论具有一个过渡区间τ1的DP,过渡区间τ1=τ(x0,x1,l)位于两个相邻非跳动FP{x0,x1}间,x0=Δ0=(1,0,…,0,0)。为减少卷积的计算,减少计算量,定义公式(28):
(28)
式中:s1,s2∈{0,1,…,dc},q1,q2∈{0,1,…,dv},dc和dv分别表示CN和VN的度。密度对(x0,y0)和(x1,y1)满足x0=y0=Δ0=(1,0,…,0,0),y1=ρ□×(x1),x1=p(ε)λ(y1)。
两个转移函数(23)转化为式(29):
(29)
式(29)适合规则SC-LDPC码,对于非规则SC-LDPC码,需根据度分布表达式做适当变换,由于篇幅限制,本文不予讨论。
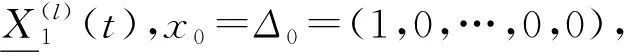
(30)
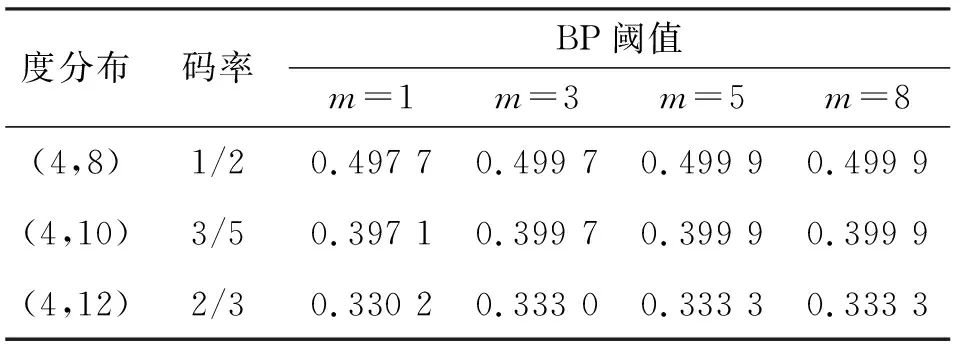
式中:αsoli,1(t1)<αsoli,1(t2),∀t1 定义19多元SC-LDPC(λ,ρ,m,L,w)在删除概率为ε的BEC上,耦合DE算法的BP阈值为 (31) 定义20多元SC-LDPC(λ,ρ,m,L,w)在删除概率为ε的BEC上,内插DE算法的BP阈值为 (32) 定理1多元SC-LDPC(λ,ρ,m,L,w)在删除概率为ε的BEC上,基于假设1和假设2,耦合DE算法的BP阈值等于内插DE算法的BP阈值。 下面通过仿真来验证内插DE算法的性能,并与传统的耦合DE算法进行对比。仿真采用有一个过渡区间τ1的DP,过渡区间τ1=τ(x0,x1,l)位于两个相邻非跳动FP{x0,x1}间,x0=Δ0=(1,0,…,0,0)。 表1给出了BEC上耦合宽度w为5,在不同度分布和m条件下,多元SC-LDPC码的BP阈值比较结果。从表中发现,相同度分布的多元SC-LDPC码,随着m增大,BP阈值增大且越来越接近香农限,尤其是从m=1到m=3,BP阈值变化很大。数值仿真角度体现了多元SC-LDPC码的阈值饱和。 表1 不同度分布和m条件下多元SC-LDPC码BP阈值比较 表2是在BEC上耦合宽度w为5的多元SC-LDPC(4,8)码在m为1、3、5、8时耦合DE算法与内插DE算法的BP阈值比较,可以看出,耦合DE算法的BP阈值与内插DE算法的BP阈值相等。 表2 内插DE算法与耦合DE算法的BP阈值比较 表3比较了两种算法在单次迭代计算过程中所需的计算量,其中w、L、m、dc和dv分别表示耦合宽度、耦合长度、每符号含有的比特数、校验节点的度和变量节点的度。可以发现,耦合DE算法由于迭代的是高维的DE递归式,因此耦合计算量与维度m有关,m增加,计算量增加。内插DE算法迭代的是一维内插函数,因此内插计算量比耦合DE算法的计算量小,特别当m很大时内插DE算法的计算量比耦合DE算法的计算量小得多。例如,对于多元SC-LDPC(4,8),m为8,w为5,L为100,耦合DE算法需要加法运算141 200次和乘法运算297 200次,而内插DE算法只需要加法运算3 400次和乘法运算8 400次。 表3 单次迭代过程内插DE算法与耦合DE算法计算量比较 图4(a)、(b)、(c)分别给出了在BEC上耦合宽度w为5的多元SC-LDPC(3,6)码、(4,8)码和(5,10)码,利用内插DE算法与耦合DE算法在m为1、3、5、8时不同信道删除概率下得到的译码波速度值,横坐标表示信道删除概率,纵坐标表示译码波速度,圆圈和点分别表示内插DE算法和耦合DE算法在不同信道删除概率下测得的速度值。当m为1时,内插DE算法测得的速度与耦合DE算法测得的速度相等;当m分别为3、5、8时,内插DE算法测得的速度与耦合DE算法测得的速度很接近,误差在[0,0.05]范围内,特别是在信道删除概率为BP阈值时,两者相等。可见,内插DE算法可对BEC上多元SC-LDPC码译码波速度起到很好的预测作用。 (a)多元SC-LDPC(3,6)码 (b)多元SC-LDPC(4,8)码 (c)多元SC-LDPC(5,10)码图4 耦合DE算法与内插DE算法测得译码波速度 总结分析仿真结果发现,与耦合DE算法相比,内插DE算法可很好地预测BEC上多元SC-LDPC码译码波速度,内插DE算法与耦合DE算法的BP阈值相等,且内插DE算法的计算复杂度要比耦合DE算法的计算复杂度小很多,尤其当耦合DE递归式为高维时。综上所述,内插DE算法以较低的计算复杂度达到了耦合DE算法预测译码波速度的效果。 针对BEC上多元SC-LDPC码BP译码算法中译码波速度分析复杂度高的问题,本文采用内插DE算法来达到既可以准确计算译码波速度又能降低计算复杂度的目的。内插DE算法利用一维内插函数在两个非跳动FP间插值密度。构造了两个转移函数来更新内插函数,将转移函数进一步转化来减少卷积运算,降低了计算复杂度。译码波的速度分析可应用于SC-LDPC码的度分布最优化设计、耦合方式设计等方面。下一步将构造并分析介于一维内插DE算法和m维耦合DE算法间的n维内插函数(13.3 BP阈值分析

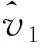
4 仿真分析
4.1 BP阈值比较
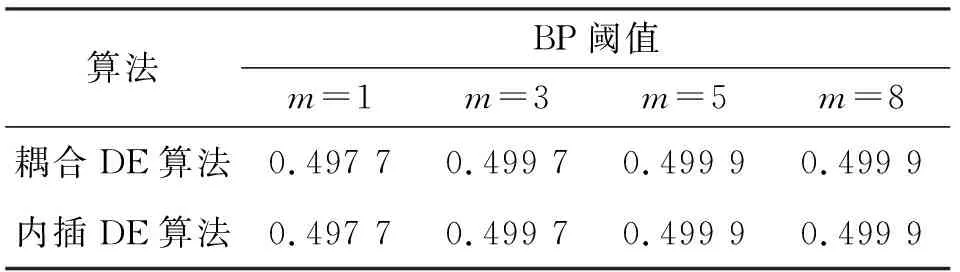
4.2 计算复杂度

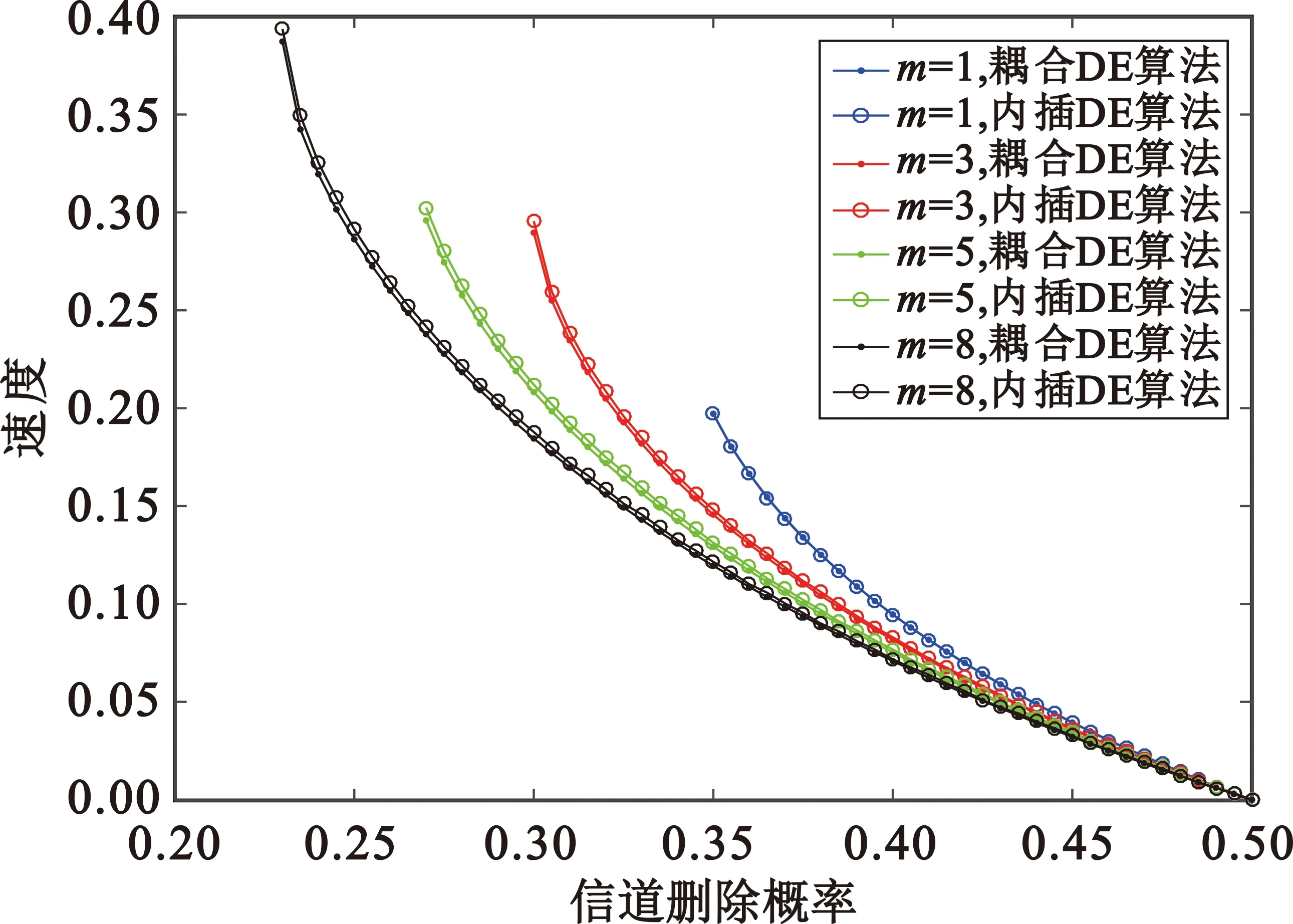
4.3 译码波速度


4.4 仿真结果总结
5 结束语

