NLOS环境下基于TOA/AOA的单基站目标跟踪*
张 毅,周霜霜,徐 川,韩珍珍,吴 奇
(重庆邮电大学 通信与信息工程学院,重庆 400065)
0 引 言
目前,公安、应急、军事等领域的机动宽带通信及定位需求越来越迫切。移动式基站在缺少先期部署通信网络或通信网络瘫痪的工作区域,可让该区域的用户获得必要的通信服务。在海上救援中,可利用船载基站计算出海上船只的位置,引导救援力量。在信息化战场上,车载基站可为作战单元提供伴随式的通信网络,同时定位士兵位置,掌控战场形势。因此,在移动场景下,利用移动式基站通信的同时实现区域性定位是一个简单、有效的方案。
随着技术的进步与发展,许多改进的单基站定位方法不断提出,在视距(Line-of-Sight,LOS)传播中可以获得良好的定位精度,但是在实际的无线电传播环境中,基站与目标之间会存在障碍物——非视距(Non-Line-of-Sight,NLOS)产生原因,这使得定位精度受到很大影响。
目前在NLOS误差消除及目标跟踪方面采用较多的是多站定位技术,利用多个基站与目标之间信息,降低NLOS传播的影响[1-3]。然而在NLOS条件下,基于多基站的目标定位跟踪方法一般难以直接应用于单基站定位中,且传统单站定位方法的定位精度受NLOS的影响较大。为此,本文研究利用单站解决在NLOS场景中的目标定位跟踪问题,采用基于扩展卡尔曼滤波器(Extended Kalman Filter,EKF)的到达时间/到达角度(Time of Arrival/Angle of Arriva1,TOA/AOA)混合定位算法实现对移动目标的NLOS消除及跟踪。由于NLOS误差存在于测量值中,而测量值体现在卡尔曼滤波器的新息值里,所以引入新息阈值来对测NLOS误差进行判断:如果新息值过大则表示测量值误差偏大,那么就舍去该新息值的信息;否则保留新息值,以此达到删除误差较大测量值的目的,从而抑制NLOS误差。最后再更新目标的状态值,实现在NLOS环境下对移动目标(Mobile Target,MT)的定位跟踪。
1 问题分析与系统建模
1.1 单站定位测量模型
测量模型如图1所示。假设目标在二维平面上移动,基站(Base Station,BS)在第k时刻的位置为(x0k,y0k),MT的状态为(xk,vxk,yk,vyk),此时的MT与BS之间的TOA值与AOA值如式(1)所示:
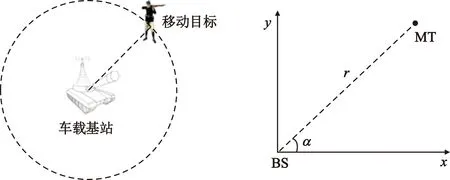
图1 单站定位图
(1)
假设目标在基站的监测区域内进行运动,二维单站测量模型的观测量Zk包括距离rk、方位角αk。在存在NLOS条件下,第k个时刻的测量值为
(2)

1.2 问题分析及思路
单站定位相对于多站定位不需要基站间的时间同步及数据交换,具有设备量小、成本低等特点,在机动性和灵活性等方面均具有显著优势。然而在复杂的环境中,目标和基站之间的NLOS传播普遍存在,此时单站定位由于本身所能获取的定位信息有限,采用传统方法使得估计出的目标位置与真实值之间存在严重偏差,因此具有一定的挑战性。1.1节描述的单站定位模型仅在LOS条件下具有较好的定位精度。
在利用卡尔曼滤波器进行目标跟踪时,由于NLOS传播会对其测量值产生很大偏差,而卡尔曼滤波器记忆性的特点使得当前时刻的测量估计值及此后的测量估计值受到影响,从而导致定位精度严重下降。因此,如何在NLOS场景中利用单基站实现对MT的定位跟踪是本文需要解决的关键问题。
针对上述问题,本文采用TOA和AOA作为扩展卡尔曼滤波器的测量值来实现对目标的定位跟踪。由于障碍物的分布一般是随机的,所以NLOS误差的分布也具有随机性的特点。NLOS误差的随机性会导致NLOS误差的剧烈波动,使得部分测量值与真实值之间存在较大偏差。这些受NLOS误差污染导致偏差较大的测量值最终会对目标位置的正确估计造成非常大的影响。若能消除这些包含较大误差测量值的影响,就可以从很大程度上消除NLOS误差。
2 基于TOA/AOA的EKF算法
本文利用扩展卡尔曼滤波的跟踪特性实现对MT的定位跟踪,同时为了解决在跟踪过程中的NLOS传播对定位造成的影响,将阈值引入到扩展卡尔曼滤波器中进行判断,对测量值进行处理,消除NLOS误差。
在常见的状态估计问题中,所涉及到的系统常常是非线性的。考虑到目标处于运动状态,基于卡尔曼滤波器基本框架下的扩展卡尔曼滤波器被提出。EKF相比于其他跟踪算法具有计算量小、运算速度快的优点。其状态方程和测量方程为
(3)
式中:Xk+1和Zk分别是状态变量和测量向量;Wk和Vk分别为过程噪声和测量误差,假定它们彼此相互独立。
扩展卡尔曼滤波器的迭代过程如下:
(4)
(5)
(6)
(7)
(8)
(9)
式中:滤波初值和协方差矩阵的初值分别为
(10)
状态转移矩阵Φk+1|k和观测矩阵H是通过求取f[·]和h[·]的雅可比(Jacobian)矩阵来获得。
2.1 基于EKF的目标跟踪
在本文中,假设目标在二维平面上移动,则扩展卡尔曼滤波的状态方程为
Xk+1=FXk+Wk。
(11)
(1)在目标做匀速运动时,本文扩展卡尔曼滤波器的参数设置为

(2)在目标做匀加速运动时,本文扩展卡尔曼滤波器的参数设置为
式中:T为采样间隔,[x,y]表示目标的位置,[vx,vy]表示在水平和垂直方向上的速度,[ax,ay]表示在水平和垂直方向上的加速度。
扩展卡尔曼滤波器的参数设置是通过对卡尔曼滤波方程系数的设定,给定初始状态量就可以对目标进行跟踪定位。在利用扩展卡尔曼滤波进行目标跟踪的过程中,目标与单站之间由于障碍物的阻挡造成NLOS传播,所以需要对NLOS误差进行消除。
2.2 基于测量值丢弃法的NLOS消除
由于NLOS传播会造成测量值出现较大的误差,并且扩展卡尔曼滤波器具有记忆性的特点,从而使得当前时刻的估计值及此后的估计值受到严重的影响。由于测量值存在较大的误差,导致目标的位置估计值与真实位置值之间存在偏差,所以应当将此测量值丢弃。在测量值被丢弃的地方,令估计值等效于预测值来进行后续的迭代计算。
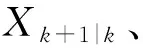
(12)
用式(12)替换式(7),进而就可依照式(8)~(9)进行后续运算。在扩展卡尔曼滤波器每次的迭代过程中都循环上述步骤,可以有效消除较大的NLOS误差,减轻对测量值的影响。
选取的门限值如果过大,则可能会造成一些NLOS误差不能被有效地滤除;如果过小,则可能会舍去过多的测量值,从而影响到目标的定位精度。本文的门限值通过反复实验获得,选取标准依据误差的大小情况来确定。实验选取角度范围为1°~10°,距离范围为5~50 m。通过60次采样,得到每个条件下误差大于10 m的采样点个数的比例,如表1所示。
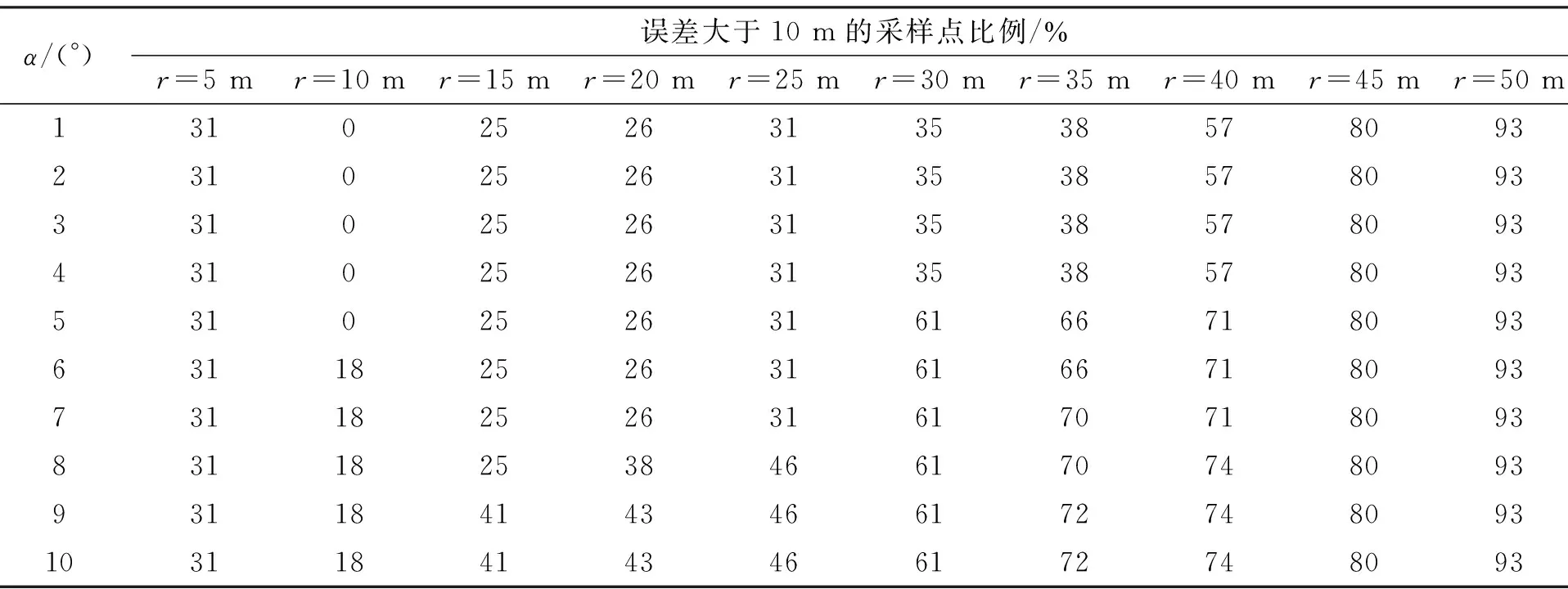
表1 误差大于10 m的采样点比例
从表1中可以看出,当距离选取为10 m,角度为1°~5°时的误差大于10 m采样点的占比最小。对这5个条件进行比较,结果如图2所示。

图2 误差对比图
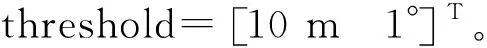
本文提出基于TOA/AOA的EKF实现NLOS误差消除及目标跟踪,具体算法如下:
Step1 获取目标真实轨迹。
假设目标做匀速或匀加速运动,根据Xk+1=FXk+Wk计算出目标的真实轨迹,以便于后续与得到的估计轨迹进行对比。
将TOA与AOA的测量值信息作为EKF的测量值输入状态方程:Z(k)=[TOA(k),AOA(k)]T+V(k)+NLOS(K)。
Step2 NLOS误差消除。
在EKF的迭代过程中,将新息与加入的阈值进行比较,改变K值,将较大误差的测量值丢弃。
if(e>threshold)
K=0;
Step3 定位。
根据基站获取的TOA与AOA值,利用EKF实现对MT的定位。
Step4 目标跟踪。
在Step 2消除NLOS误差的基础上,根据Step 3求得的目标位置,通过EKF的迭代累计,可以得到MT的估计轨迹,实现目标跟踪。
3 仿真与分析
本文在Matlab中进行仿真实验,假设基站以圆心(200,300) m、半径50 m、角速度π/60×T进行圆弧运动,扩展卡尔曼滤波器的采样间隔T设置为0.5 s,采样次数N为50。假设系统的距离测量误差服从均值为0、方差为100的高斯分布,角度测量误差服从均值为0、方差为0.000 001的高斯分布,NLOS误差服从均值为300的指数分布,目标轨迹不考虑多普勒效应对定位的影响。
最后,采用均方根(Root Mean Squar,RMS)误差作为模型的评价标准,即
(13)

将本文提出的改进EKF-TOA-AOA算法与文献[4]的自适应跟踪算法、EKF、UKF算法进行对比分析。
在目标做匀加速运动的过程中,假设目标从初始位置为(1 000,5 000)m处以(10,50)m/s的速度匀速运动,EKF的目标位置初值选取为(1 005,5 005)m。图3是这四种算法与目标真实轨迹对比图,图4是均方根误差对比图。

图3 匀速运动轨迹跟踪图
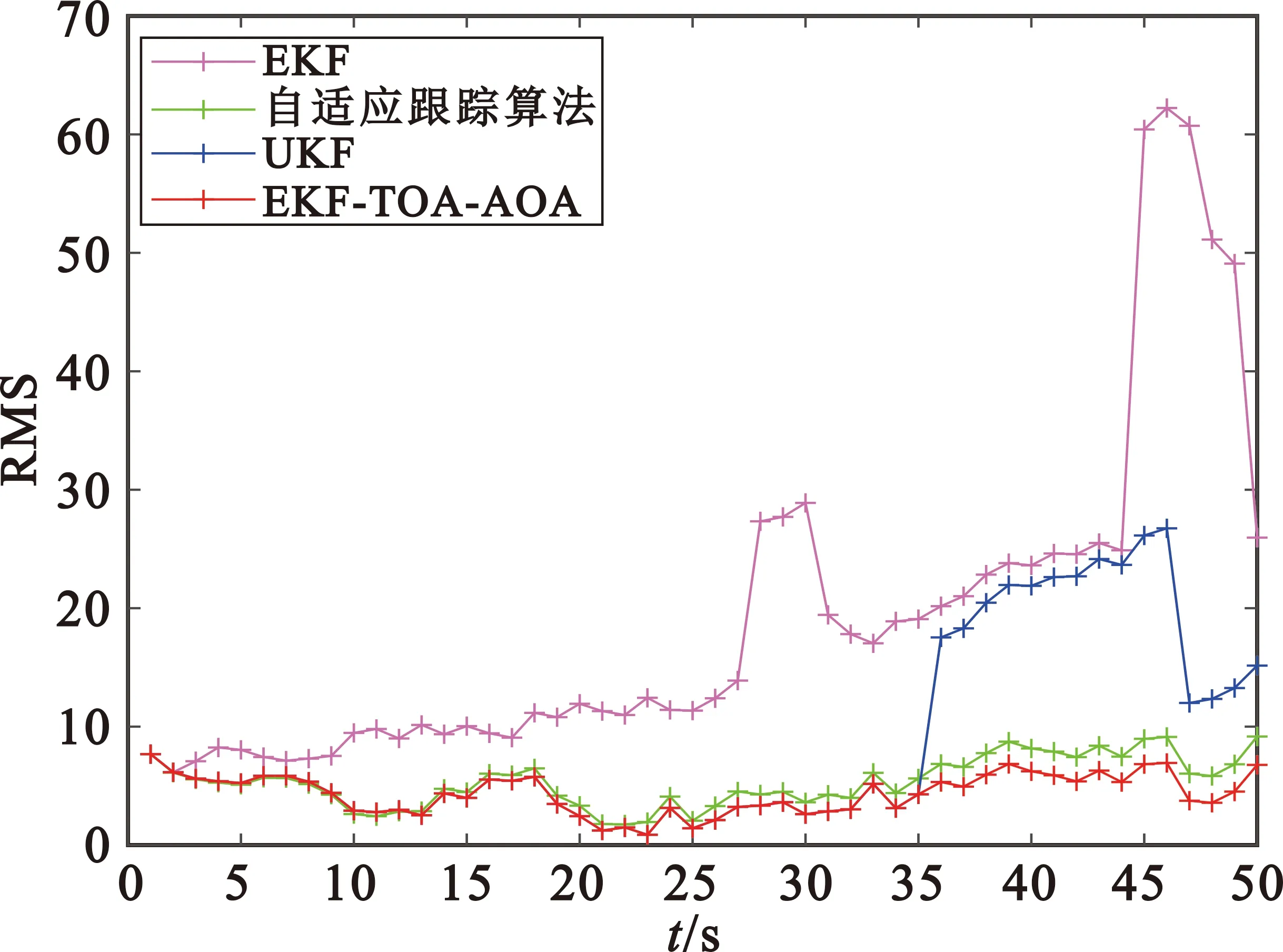
图4 匀速运动RMS定位误差
从图3和图4 的仿真结果可以看出,在匀速情况下,本文提出的改进EKF-TOA-AOA算法的均方根误差曲线位于最底层,与自适应跟踪算法定位性能相近,但是自适应跟踪算法使用的是多基站。此外,它又比单独使用EKF、UKF算法的定位性能好,获得的估计误差更小,估计的轨迹更接近真实轨迹。这是因为使用TOA/AOA混合定位方法不仅可以减少基站的数量,而且在定位精度上也比单个定位方法高。从图4中可以看出,使用卡尔曼滤波器算法的误差有逐渐增大的趋势,这是因为卡尔曼滤波器的记忆性,当前一个时刻目标估计状态出现偏差,可能会影响到后续的结果。尽管如此,本文算法的性能仍然是最优的。
在目标做匀加速运动的过程中,假设目标从初始位置为(-100,200)m处以(10,50)m/s的速度、(2,-4)m/s2的加速度运动,EKF的目标位置初值选取为(-95,195)m,图5和图6分别是几种算法的轨迹跟踪图与定位误差图。
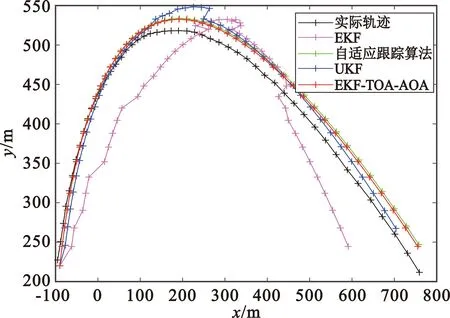
图5 匀加速运动轨迹跟踪图

图6 匀加速运动RMS定位误差
从图5和图6的仿真可以看出,在匀加速情况下,EKF算法的定位精度明显下降,其他三种算法仍然具有较好的定位性能。几种算法都存在一定误差,不过本文算法的定位性获得的估计误差更小,估计的轨迹更接近目标轨迹。
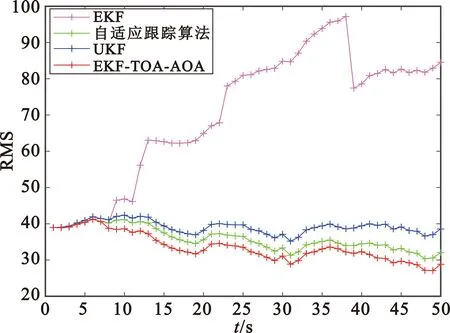
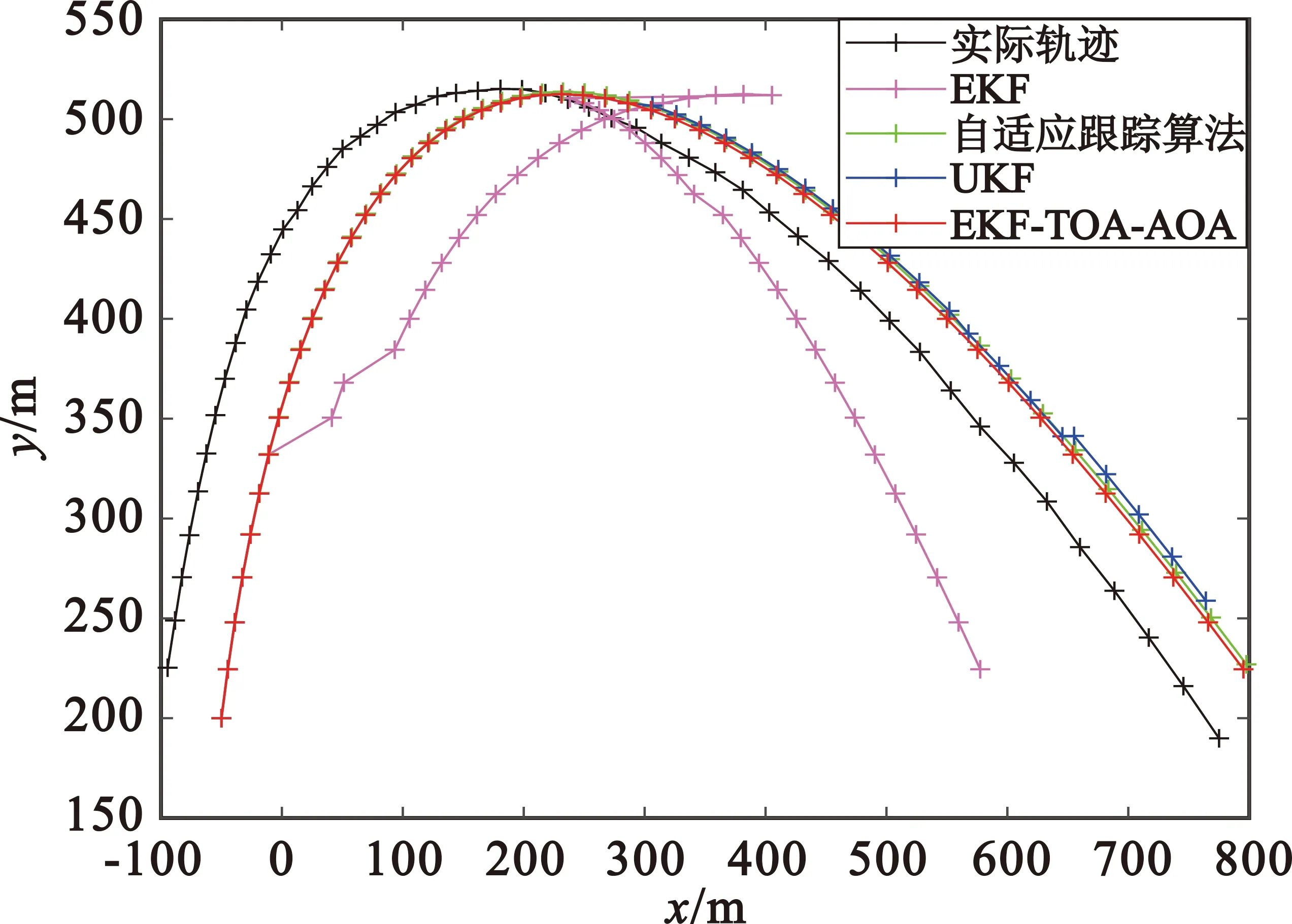
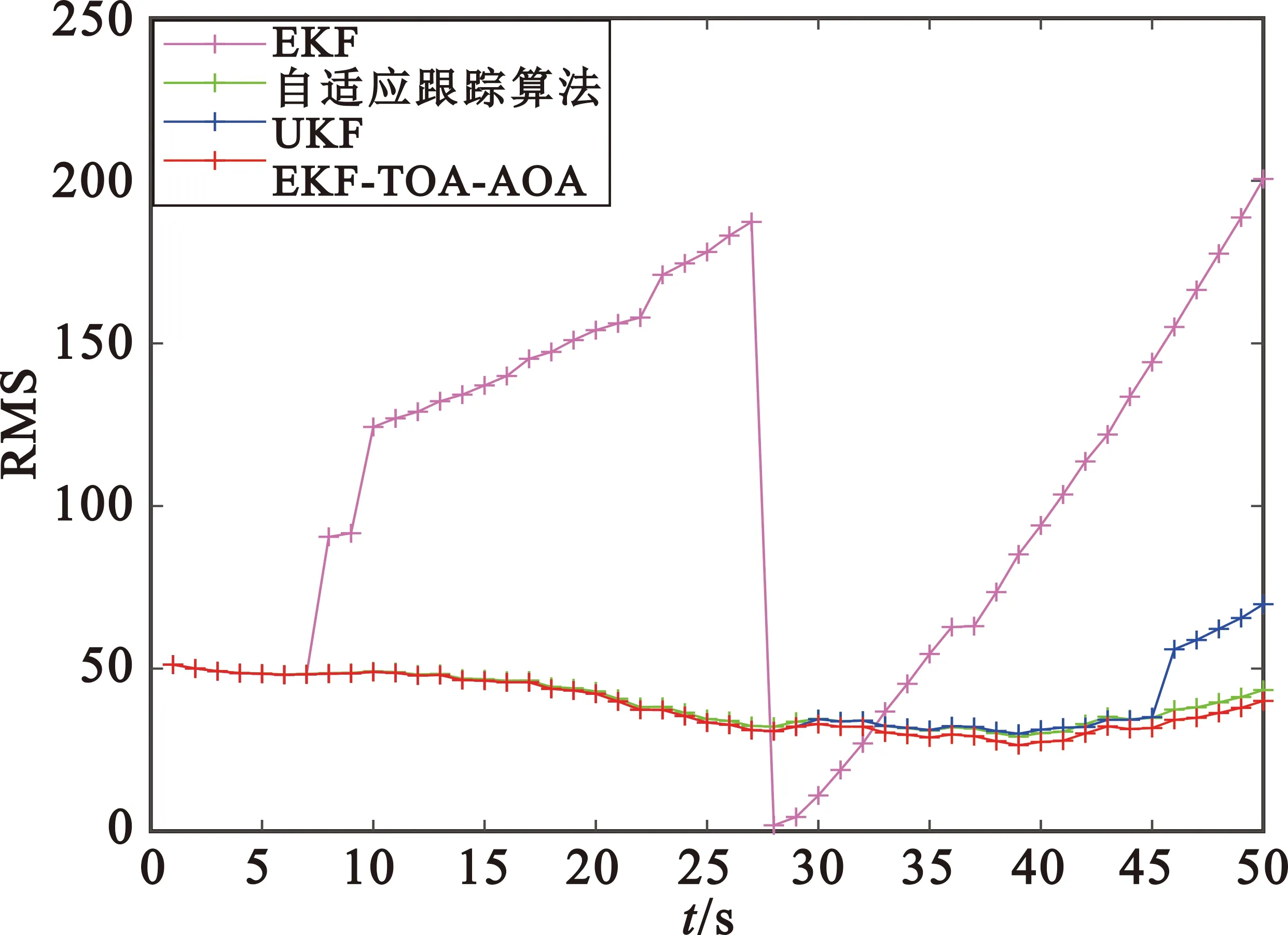
由于在实际环境中,一般无法得到较为精确的目标初始值,所以在匀速情况下将EKF的初值重新设置为(1 035,5 035)m,得到的轨迹跟踪及误差图如图7所示。在匀加速情况下将EKF的初值重新设置为(-50,220)m,得到的轨迹跟踪及误差图如图8所示。
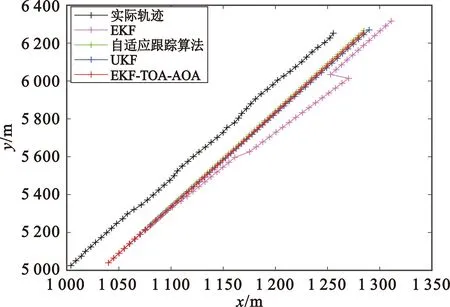
(a)轨迹跟踪图
(b)RMS定位误差图图7 匀速运动
(a)轨迹跟踪图
(b)RMS定位误差图图8 匀加速运动
从图7和图8可以看出,在无法得到较为准确的目标初值时,所有算法的定位性能都严重下降,且由于卡尔曼滤波器的记忆性特点,导致后续计算受到影响,估计的轨迹偏离严重,但是本文算法的误差仍小于其他三种算法。
综上所述,本文的改进算法具有较低的RMS误差曲线,优于传统的滤波器算法。
4 结束语
单站定位技术不要求基站间的时间同步,且在实际作战场景中,具有成本低、灵活性和机动性高等优势。本文主要针对在NLOS场景下的单站定位存在定位精度低的问题做出相应的改进,提出了一种基于EKF的TOA/AOA单站定位技术。该算法通过将门限值加入扩展卡尔曼滤波器中进行判断,以此滤除较大误差的TOA/AOA测量值,同时实现对目标的定位跟踪。仿真结果证明了EKF-TOA-AOA算法的有效性,在一定程度上可以抑制NLOS误差,具有较高的定位精度。由于实践中无法得到较为精确的目标初值作为卡尔曼滤波器的初始状态,所以后续将进一步研究卡尔曼滤波器的初值问题,使得其在工程实践中更好地应用。

