Gm-APD 激光雷达的双参量估计透烟雾成像算法

张银波，李昊阳，孙剑峰*，李思宁，姜 鹏，侯 跃，张海龙

（1. 哈尔滨工业大学 光电子技术研究所 可调谐（气体）激光技术重点实验室，黑龙江 哈尔滨 150001；2. 复杂系统控制与智能协同技术重点实验室，北京 100074）

1 引 言

Gm-APD 激光雷达在室外成像的过程中，天气的改变严重影响其成像结果，特别是云雾、烟雾等散射介质。颗粒对激光有较强的散射和吸收能力，导致回波信号信噪比下降，激光雷达探测距离缩短，成像能力严重受限［1］。因此，研究激光与烟雾相互作用的散射机理、分析烟雾后向散射回波特点以及建立烟雾散射回波模型，对于烟雾后向散射抑制、精确提取目标回波信号、提高激光雷达的探测能力和环境感知能力尤其重要。

光子在烟雾中传输时，与粒子之间发生多次散射，接收到的回波光子在时域上满足一定的分布规律。目前，对于单光子激光雷达烟雾回波信号的研究主要以分布模型拟合去雾法为主。该技术通过拟合接收光子在时域上的分布，利用目标信号与烟雾信号分布的不同来实现去雾。其中，美国麻省理工学院（MIT）在分布模型拟合去雾中率先提出了Gamma 分布模型。2018 年，Satat 等［2］通过观察发现，烟雾回波光子与目标回波光子分别满足Gamma 分布和高斯分布，通过极大似然估计得到Gamma 分布的两个参数，随后将目标光子从烟雾散射光子中分离，最终实现烟雾的去除。在不同的烟雾光学厚度下，达到了较好的重建效果。不同于Satat 提出的Gamma 分布理论，2020 年Sang［3］等提出了基于激光雷达物理模型估计雾轮廓线的去雾算法，同时采用期望最大化（EM）算法进行参数最优化搜寻。同年，Mau［4］等 利 用EM 算 法 将SPAD 阵 列 中 每 个 像 素点的探测概率曲线拟合为对数正态分布与高斯分布的混合分布，并依据高斯分布参数得到目标距离信息。哈尔滨工业大学［5-10］开展了基于Gm-APD 激光雷达的烟雾后向散射机理研究，建立了适用于Gm-APD 激光雷达的后向散射光子分布模型。根据具备远距离探测能力的Gm-APD 激光雷达，提出多种基于Gamma 模型参数估计的雾天激光雷达重构算法，并在室内、室外环境中验证了模型和算法的能力。

以上研究表明，目前的单光子激光雷达透烟雾成像主要以基于Gamma 模型参数估计的烟雾去除为主导。估计算法主要通过极大似然估计直接获取Gamma 函数的两个参数，并未对两个参数的关系进行讨论。此外，目标峰的存在影响烟雾回波信号的估计精度，降低图像的重构质量。

针对上述问题，本文从Gamma 模型参数关系推导和重构算法两个方面展开研究。首先，介绍了基于Gm-APD 激光雷达的触发模型以及根据探测概率求解实际接收的回波信号原理，基于光子与烟雾粒子的碰撞理论，以Mie 散射理论为基础详细推导Gamma 模型的两个参数，并且建立衰减系数μ与散射次数k之间的物理关系。根据推导的μ，k关系式提出一种双参量估计算法，考虑了如何精确估计μ，k两个参数。最后，利用仿真实验检验μ，k关系式的正确性，利用室内实验验证了提出算法的透烟雾成像能力。

2 透雾理论模型

2.1 Gm-APD 激光雷达触发模型

Gm-APD 激光雷达在探测的过程中，目标光子和噪声光子组成的回波信号入射到探测器光敏面上实现光电子转换。目标反射光子和噪声光子均满足Poisson 分布，因此，在t1和t2探测时间间隔内产生k个光电事件的概率［9，11］为：

式中：M（t1，t2）为在时间区间（t1，t2）内探测器探测到的回波光子数。

Gm-APD 在时间t1和t2之间不发生触发，即产生0 个光电子事件的概率为exp［-M（t1，t2）］。产生光电事件的概率为1-exp［-M（t1，t2）］。然而，由于探测器死时间的存在［16］，第i个时间bin的探测概率与之前时间bin 的探测概率有关。若门控时间小于探测器死时间，在距离门内Gm-APD 探测器只能响应一次光子计数信号，即单次触发模式。因此，第i个时间bin 中的探测概率为［17］：

根据探测得到的探测概率曲线，结合式（2）可以得到第i个bin 内的回波光子数为：

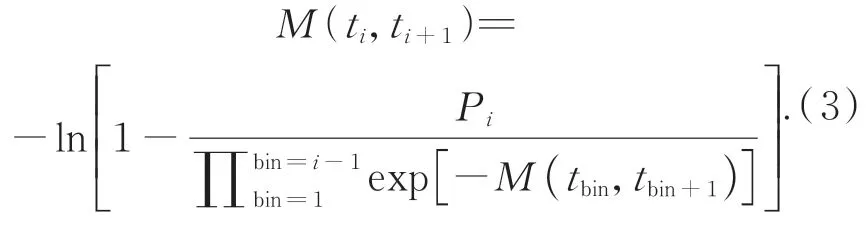
通过求解距离门内每个时间bin 内的光子数，最终得到实际接收的回波信号。本文的主要工作就是基于实际接收的回波信号进行目标信号的提取与图像重建。

2.2 基于Gamma 模型的参数推导

由于烟雾颗粒对激光具有强散射和吸收作用，激光在烟雾中传播时的回波能量随距离的增长呈e 指数衰减，并且激光传输时光子存在连续散射事件，每个散射事件相互独立，多个独立指数随机变量的总和服从Gamma 分布。其表达式如下［2］：

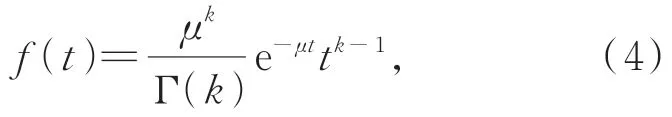
式中：μ代表衰减系数，k代表碰撞次数。

Gamma 模型涉及的两个参数，衰减系数μ和碰撞次数k，均与激光在烟雾中的传输过程密切相关。本文从光子与烟雾颗粒的碰撞过程这个微观角度出发，推导这两个参数的关系。

激光在烟雾中传播时其衰减满足朗伯比尔定律：

式中：Iin，Iout分别为激光透过烟雾前后的光强，μ为介质的衰减系数，l为激光在介质中传播的距离。

将式（5）变形得到衰减系数μ的表达式为：

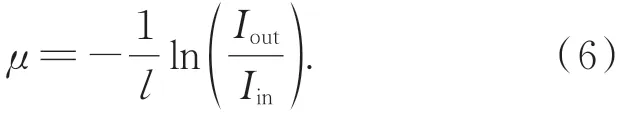
假设一次成像过程结束后，全部光子的碰撞次数的均值为k，由米氏理论可知光子与散射介质颗粒发生单次碰撞会损耗能量，损耗的比例为散射效率因子与消光效率因子的比值，即Qsca/Qext。

散射效率因子与消光效率因子的求解公式如下［12］：

式中：α=πd/λ，为烟雾颗粒的尺寸因子；d为烟雾平均粒径；λ为激光波长；an，bn为Mie 散射系数，他们的值与粒子尺寸因子α和介质颗粒复折射率m密切相关［18］。

当激光在衰减系数为μ的散射介质中传输l路径时，与烟雾颗粒发生k次碰撞后的光强近似满足以下关系：

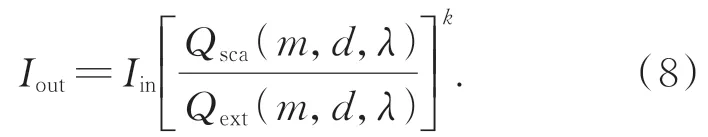
将式（8）带入式（6）中得到Gamma 函数两个参量μ和k之间的关系，即：

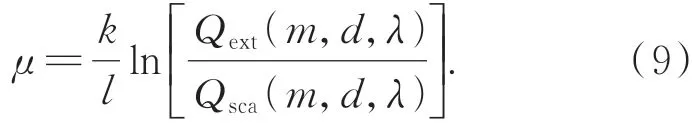
可以看出，衰减系数μ与散射次数k满足线性关系，即随着散射次数k的增加，衰减系数μ呈线性增大的趋势。然而，增大的斜率与烟雾自身的消光系数、散射系数和激光在烟雾中传输的长度等参量有关。相较于文献［2］中模型参量的定义，本文从Mie 散射理论出发，建立了衰减系数μ与散射次数k之间的物理关系。

2.3 透雾重建算法

Gm-APD 激光雷达透雾成像的关键是能够精确地估计烟雾的散射信号，进而实现烟雾散射光子的抑制。基于Gamma 分布模型的烟雾回波信号估计，其研究核心是实现两个参量μ与k的精确估计。不同于采用极大似然估计算法直接求解μ与k［2］，本文的参 量估计算 法 是基于2.2 节中μ与k的线性关系估计这两个参数的。

参数估计主要采用两步策略。第一步是利用Gamma 模型的数学性质求解衰减系数μ。由式（4）的Gamma（μ，k）可知，其均值E和方差D分别 满 足E=k/μ，D=k/μ2。衰 减 系 数μ为 均 值E和方差D的比值，即μ=E/D。根据式（3）计算得到的回波信号，可以得到每个像素接收回波信号的均值E和方差D。第二步是利用本文推导得到的μ，k关系求解k。其中，传输距离l为实际目标距离，散射效率因子与消光效率因子可根据实际的烟雾类型确定。

由于回波信号中包含目标反射光子与烟雾散射光子，这严重限制了均值E和方差D的求解。因此，这里采用DOG 小波函数对回波信号进行连续小波变换［19］，通过峰值选取确定目标回波峰并进行去除。

本文提出的基于μ，k线性关系的双参量估计算法，通过估计面阵Gm-APD 激光雷达中每个像素的回波信号来实现烟雾干扰抑制。算法的具体流程如图1 所示。

图1 双参量估计算法处理流程Fig.1 Processing flow chart of dual-parameter estimation algorithm

3 实 验

为了检验本文提出算法对烟雾干扰的抑制能力，开展了室内高浓度烟雾条件下的Gm-APD激光雷达透雾成像实验，如图2 所示。Gm-APD激光雷达采用激光脉冲飞行时间测量（TOF）方式获得目标的三维距离信息。探测器的触发信号为激光脉冲同步信号。采用FPGA 实现控制命令的发送以及图像数据的传输。目标的三维图像在计算机上显示。雷达的具体参数见文献［9］。

图2 Gm-APD激光雷达透雾成像实验示意图及场景Fig.2 Schematic diagram and experimental scene for Gm-APD lidar imaging through fog

为了减小烟雾的扩散范围、提高其分布的均匀性，本实验采用长度为1 m，直径为450 mm 的塑料箱作为烟雾箱，其两端安装具有90%透过率的光学透镜。烟雾箱前端与雷达的距离为5 m。目标在烟雾箱后端。本文的烟雾发生器可产生粒径分布为1～2 μm 的颗粒，1 064 nm 激光对应的复折射率与煤烟型颗粒折射率接近。

为避免背景光子对实验结果的影响，本文的实验在暗室中进行；当烟雾箱中不充入烟雾时，对目标进行探测，利用传统的峰值算法进行图像重建，并将这些成像结果作为无烟雾时的标准图像；利用烟雾发生器向雾箱内充入烟雾，待烟雾在雾箱中扩散均匀后，利用激光雷达透过烟雾对目标进行数据采集；利用不同的算法对有烟雾的图像进行去雾成像，并与标准图像进行对比，检验算法的去雾成像能力。

4 结果与分析

4.1 蒙特卡洛仿真验证

为了验证式（9）的正确性，本文首先利用蒙特卡洛算法实现烟雾环境下的回波信号仿真。在仿真中，选用煤烟型颗粒的复折射率，m=1.75i～0.44i［13］，烟雾颗粒平均粒径d为1 μm［14］，激光波长λ为1.064 μm。通过调节能见度参数，实现不同烟雾浓度条件下的激光后向散射回波光子分布的仿真。 蒙特卡洛仿真算法见文献［7］。

当能见度V为0.12 km 时，回波光子的时域分布结果如图3（a）所示。可以看出，回波信号主要为双峰分布，第一个峰为烟雾散射光子，第二个峰为目标峰。为了提高Gamma 拟合参数估计结果的准确性，估计算法只需要对烟雾散射光子进行讨论。因此，需要对回波信号中的目标回波信号峰进行剔除。此处选用一次函数代替目标回波峰，对处理后的数据进行Gamma 拟合得到标准的模型参数。去除目标峰后的拟合结果如图3（b）所示，Gamma 模型拟合结果与原始数据更贴切。

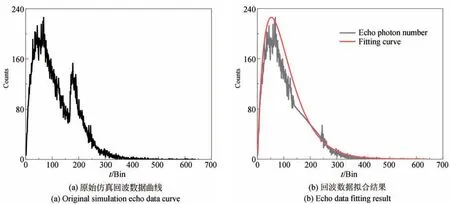
图3 仿真数据及拟合结果Fig.3 Simulation data and fitting results

为了提升数据分析的合理性与精度，在每个能见度下进行多次仿真，并且对去除信号峰后的数据进行拟合。表1 所示为能见度V从0.12 km增加至0.16 km 时的拟合结果及误差分布。标准参数μ，k是由十组数据拟合的参数求均值得到。 当V=0.12 km 时，k的 标 准 值 均 值 为1.944，方差为0.013。由表1 可知，利用μ，k关系公式计算的参数与极大似然估计的参数误差均在7%以下，证明了式（9）的有效性。

表1 不同能见度条件下公式求解参数的误差分布Tab.1 Error distribution of formula solution parameters under different visibility conditions

4.2 室内实验数据处理与分析

4.2.1 单个像素参数估计

为了检验本文提出算法对烟雾回波信号的估计能力，对室内透雾成像数据的单个像素回波进行拟合。选择像素点（20，45）的信号进行分析，结果如图4（a）所示。回波中包含两个信号峰（烟雾散射信号和目标信号），烟雾散射信号的强度大于目标的回波信号，并且目标峰在烟雾回波信号的下降沿内。

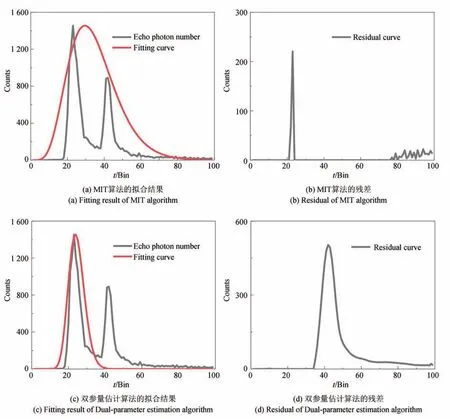
图4 单个像素回波信号的拟合结果Fig.4 Fitting results of single pixel echo signal

分别利用文献［2］中MIT 的拟合算法和本文提出的算法对这个回波信号进行估计。值得注意的是，这两种算法都是直接估计计算得到回波光子信号。我们研究的重点是对包含烟雾散射光子和目标反射光子的回波信号进行估计。然而，两种算法的拟合结果差别较大。从图4（a）中可见，MIT 算法的拟合效果较差。这是由于目标回波峰的存在影响了Gamma 拟合的精度。Gamma 拟合得到的曲线将目标回波覆盖，导致在对消过程中目标信息的丢失。从图4（c）中可见，双参量估计法的拟合效果更优。算法通过两步策略的估计方式，实现了只对烟雾回波峰数据的拟合，抑制了目标信号对估计结果的影响。

分析图4（b）和4（d）两算法的残差分布可知，MIT 算法残差分布中的目标信息完全丢失，错误地将烟雾的回波信息当作目标回波信息。双参量估计算法残差分布图中目标信息保留完整，克服了烟雾回波残差对目标信息提取精度的影响，提高了对烟雾背后目标信息的感知能力。

4.2.2 室内透雾图像重构

为了检验提出算法对烟雾背后目标的成像能力，本文对面阵Gm-APD 激光雷达64×64 个像素的回波信号进行目标光子提取，并且与传统算法进行对比。重建图像如图5 所示，可以看出，本文提出算法重构的距离像与强度像均优于峰值法和MIT 算法。

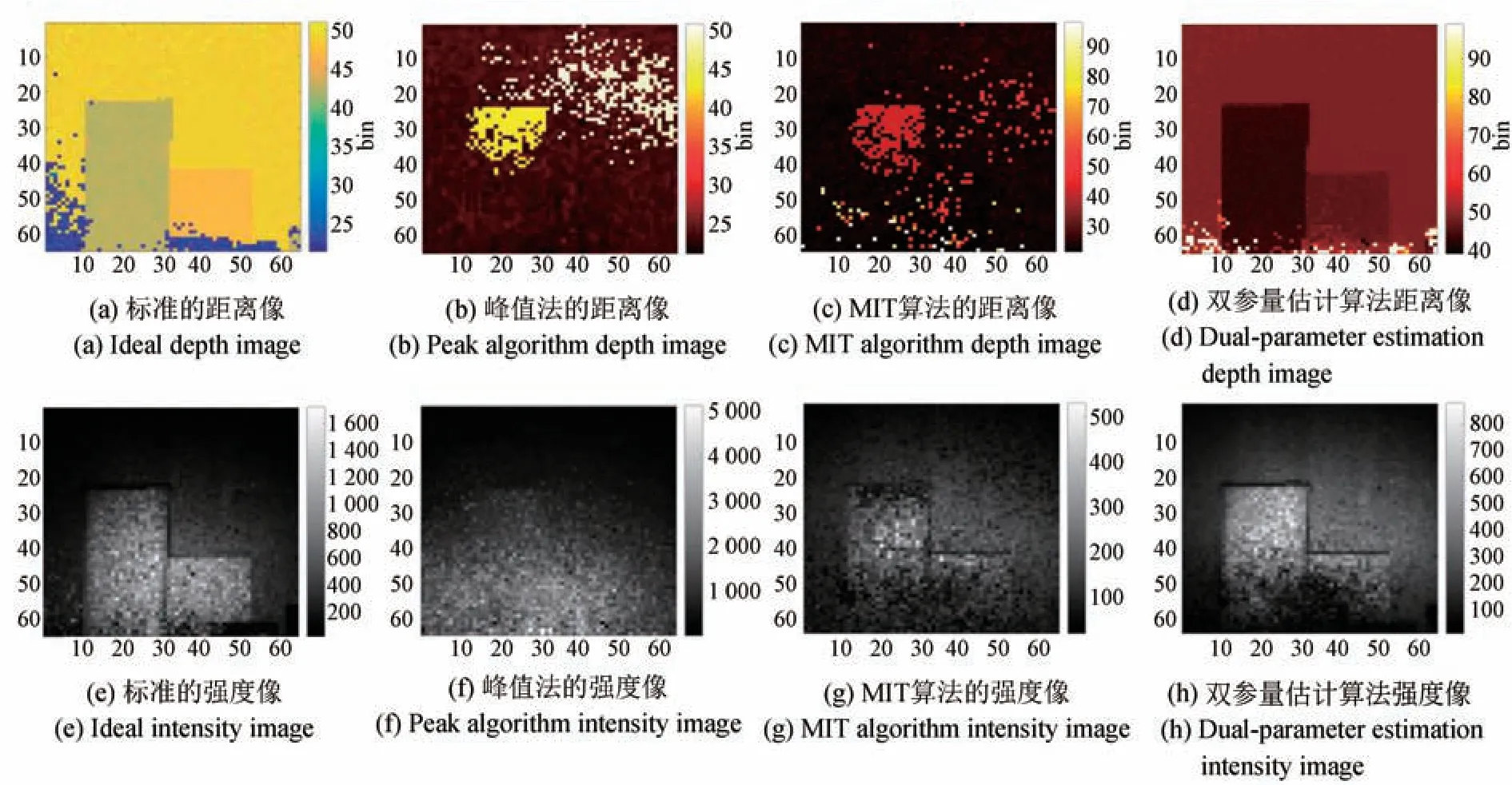
图5 不同算法的图像重建结果Fig.5 Image reconstruction results of different algorithms

由距离像可知，峰值法与MIT 算法重建的图像不能识别和保留目标像素点的信息，无法重构出浓雾背后的目标轮廓信息和深度信息，这两种算法的抗烟雾干扰能力较弱。而双参量估计算法很好地恢复了被烟雾遮挡目标的轮廓信息，较好地重构出目标的深度图像。

由强度像可知，峰值法和MIT 算法对强度像的恢复程度较低，两个目标反射光的强度与背景融为一体，很难区分目标的轮廓。双参量估计算法重构的强度像清晰反映了目标表面的强度分布情况，与背景明显地分离开。

为了对比3 种算法的重建能力，本文选用结构相似性（Structural Similarity，SSIM）［20］和目标复原度（Target Recovery，TR）［9］两个指标来评价算法的图像重建效果。SSIM 取值为［0，1］，SSIM 越大，图像失真越小、图像效果越好；TR 值越大，算法对场景的复原能力越强。

3 种算法重建图像计算的评价指标都是基于标准图像得到的，结果如表2 所示。相对于峰值法和MIT 算法，本文算法具有最大的SSIM 和TR。与MIT 算法相比，本文算法重建强度像的SSIM 提高了0.228 9，距离像的TR 提高了73%。这表明本文提出的双参量估计算法在面阵Gm-APD 激光雷达透烟雾成像中具有更强的烟雾抑制能力和目标感知能力。

表2 不同算法处理图像的评价指标Tab.2 Evaluation index of image processed by different algorithms

5 结 论

为了提高Gm-APD 激光雷达对浓密烟雾背后的目标的成像质量，本文对MIT 提出的Gamma 分布模型进行了完善，提出了一种基于双参量估计的Gm-APD 激光雷达透烟雾成像算法，主要包括Gamma 模型参数关系推导和重构算法两个方面。首先，介绍了基于Gm-APD 激光雷达的触发模型以及根据探测概率求解实际接收的回波信号原理，并且基于光子与烟雾粒子的碰撞理论和Mie 散射理论详细推导了Gamma 模型两个参数的物理关系。根据推导的关系式提出一种双参量估计算法，并开展了仿真和室内透雾的实验。实验结果表明，双参量估计算法的重构效果优于MIT 算法，重构的强度像的结构相似性提高了0.228 9，重构的距离像的目标复原度提高了73%。该研究有效提升了Gm-APD 激光雷达在烟雾环境中的目标感知能力，拓展了复杂环境下Gm-APD 激光雷达的应用范围。