弯曲河道型库岸滑坡涌浪传播及其与大坝的相互作用
彭 辉,黄亚杰
(三峡大学 水利与环境学院,湖北 宜昌 443000)
1 研究背景
弯曲河道型水库库区因极端气候、地震和不良地质等条件的影响,易导致失稳的变形体引起的巨大滑坡涌浪,不但会对沿岸的居民和过往的船只造成威胁,而且还会危及大坝的安全。因此研究弯曲河道型库区滑坡涌浪传播规律及其与大坝作用过程有着重要意义[1-2]。
许多复杂因素都可以影响弯曲河道型水库库区滑坡涌浪传播,比如地形地貌、滑坡体大小等,因此经验公式成为了一种简要的计算手段,常用的经验公式有许多比如潘家铮法、水科院法、Noda E、美国土木工程学会法[3]。国内外多位专家和学者,根据不同滑坡体的几何形状、材料、入射角度等特征因素对滑坡涌浪的影响开展了深入研究,研究手段有水工物理模型试验和数值仿真分析[4-5]。对于数值仿真分析滑坡涌浪有以下两种方式简化:①简化流体力学的方程模型[6];②简化计算模型[7]。这些简化方法的弊端在于没有考虑地形的实际情况,而且很少考虑涌浪与大坝的相互作用和下游大坝对涌浪传播的影响。对于水工物理模型试验需要大量的财力和人力支持,由于客观条件又不能获得准确数据,限制了其推广。
本文针对文献[8]基于Flow-3D对其水工物理模型进行三维数值模拟。通过对物理试验模型1∶1比例建模,充分考虑地形因素采用弯曲河道并在河道尾部增加重力坝。采用有限差分法进行水流和水力学模拟分析滑坡涌浪在弯曲河道中的传播规律[9],通过三维数值模拟得到滑坡涌浪的传播的完整的数据,进而研究了涌浪与大坝的相互作用规律[10]。
2 弯曲河道型库岸滑坡涌浪的物理模型实验简介
水工物理模型主要由滑坡体、滑动控制板、河道滑坡区、水库扩大段和弯曲型河道构成。物理模型试验采用不同滑坡体体积、水深、入水角度、落差等影响因素,研究了滑坡激起涌浪变化特点,并结合实验数据拟合出首浪高度计算公式[11]。具体模型如图1所示。

图1 弯曲河道模型实物图Fig.1 Physical model of curved river channel
3 基于Flow-3D的滑坡涌浪数值模拟
3.1 基本理论
Flow-3D采用有限差分法来对控制方程进行数值离散求解,利用极小残差算法求解,该算法具有相对收敛快、精度高的特征,广泛应用于计算流体[12-13]。波浪在Flow-3D软件中被视为不可压缩的粘性流体[14],所以流体运动控制方程为Navier-Stokes连续性方程。计算的流体视为牛顿流体。滑坡体下滑时将会导致水面出现剧烈的抖动与变形。因此将采用RNKκ-ε紊流模型来计算。RNKκ-ε湍流模型可以很好模拟流线弯曲的流动[15-16]。通过面积分数和体积分数来定义有限元网格中的物体,有限元网格能够通过流体体积(VOF)法精确地模拟出复杂的几何形状,还可以模拟三维流体的流场分布以及不同液体静止或者运动复杂界面相互作用的液面变化。
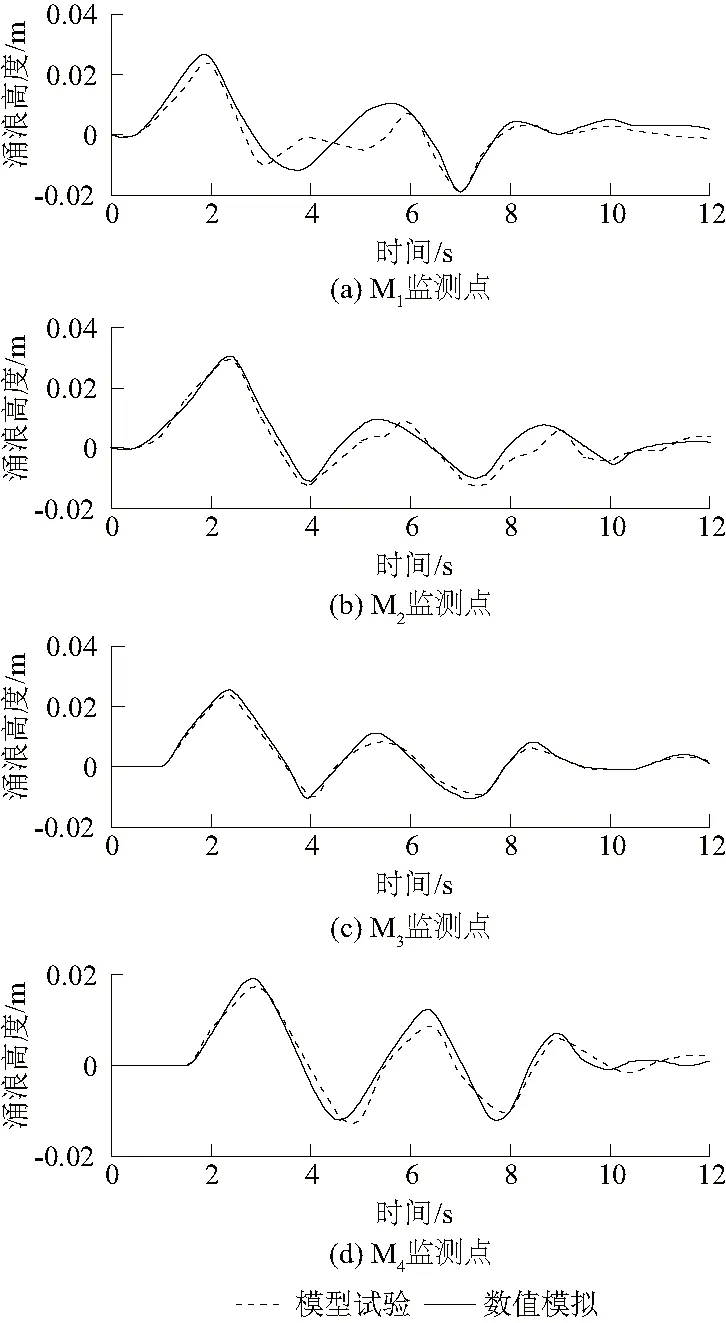
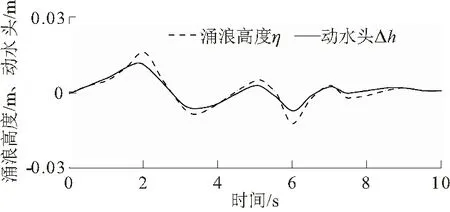
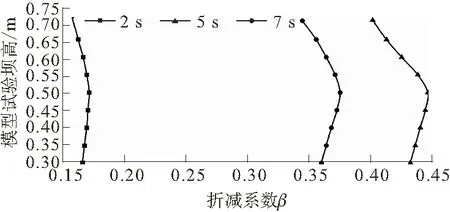
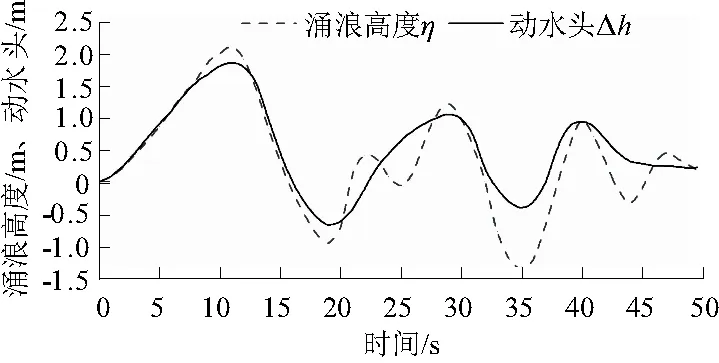
它的计算原理就是定义一个单元流体函数,称为F(单元内所占流体体积除以该单元可容纳流体体积)。F=0表示单元内没有流体;F=1表示流体完全充满单元;0 3.2.1 模型的边界条件和初始条件的设定 三维数值模型中,本文将固体和流体接触面的边界条件设定为墙壁(wall)边界条件,水槽的侧壁和底部视为光滑无摩擦的自由液面,流体法向速度等于0。流体表面采用自由液面边界条件,设置为一个标准大气压强。 模型运动学边界条件为 (1) 模型动力学边界条件为 (2) 式中:η为波浪表面相对静止水面高度;∇φ为自由表面上所有速度分量变化率,∇η为各方向水头变化率,φ为各方向水流速度;g为重力加速度。 将试验滑块简化为矩形刚性滑块,模拟在无摩擦情况下整体滑入水中,滑块仅受重力,不考虑空气阻力。水槽中的水静止,所有网格初始速度设定为0,滑块以起始静止状态下落。重力加速度g=9.81 m/s2,水的密度ρw=1 000 kg/m3。为了验证三维数值模型与水工物理模型试验结果的准确性以及可行性,滑块选择了水工物理试验产生最大首浪高度所用试块尺寸为0.4 m×0.3 m×0.3 m(长×宽×高),滑块密度为2 400 kg/m3。 3.2.2 模型的尺寸及网格划分 为了满足与实际中滑坡的相似性,大多数河道的河流转角处的弯折角度都在60°左右,故将河道模型弯折角设置为60°。滑坡体入水方向与水流方向垂直。河道前部滑坡区域尺寸为1 m×1.3 m;弯曲河道段长2.5 m,宽0.5 m,高1 m,河道截面为矩形。水库段模型采用突变扩大段链接。水库区尺寸1.1 m×1.5 m,滑板长1.5 m,宽度为0.5 m,滑动面角度调节范围为40°~90°。坝体为直立混凝土重力坝。三维数值模型具体尺寸如图2所示。 图2 弯曲型河道模型尺寸Fig.2 Dimensions of curved river model 在Flow-3D软件中,网格划分密度与模型计算精度、模拟效果呈正相关。因此,本文几何模型计算区域采用均匀的矩形交错网格,将几何模型导入Flow-3D软件(STL格式),共计2×106个。通过流固耦合模型(GMO)来模拟刚体的运动。计算时间步长为0.062 5 s,计算时间为5 s。图3显示初始水位0.7 m、入射角60°、滑块入水速度2.54 m/s的三维数值模拟示意图。 图3 三维数值模拟示意图Fig.3 Three-dimensional numerical simulation 水工物理模型试验监测点布置在图2中M1—M4,这些监测点的数据作为对比值是因为滑块入水时产生涌浪效果显著。以0.8 m为初始水位、入射角为60°、水面大气压为0.1 MPa,来分析滑坡涌浪在弯曲河道中的传播规律。 滑块在自重作用下,沿着斜面由静止开始向下滑至水面并开始挤压水体引起大尺度紊流,涌浪由落水点向四周转播形成巨大浪花,附近水域水体迅速升高,最终形成了初始涌浪。初始涌浪在岸坡上爬至最高后水体下落与后续涌浪叠加传入河道。河道左岸水域水面迅速抬升,在左岸爬升到最高处后迅速下落,并与后续传来的波峰相互作用和震荡。库区水体也随着落水点形成的涌浪传播圈升起、降落,推动着涌浪不断向坝前传播。在首浪驶出弯曲河道来到水库扩大段传至坝前,由于坝体的阻挡,坝前水位持续升高,坝前水位达到最高。随后坝前水位回落,涌浪在河道内相互震荡,涌浪波能损失,波高随着能量的损失开始逐渐降低。虽然还有后续残余的波浪向大坝方向传播,但是水面逐渐趋于稳定。 将相同工况下的监测点同水工物理模型结果进行对比,滑块入水的瞬间作为开始计时点,数值模型与物理试验对比结果如下。 由数值模拟计算值与水工物理模型实测值对比(图4)可以得出:①监测点M2的首浪数据明显高于其他监测点数据,说明涌浪首浪对河道凹岸冲击较大;②监测点离落水点越远,误差值越小;③各监测点数值模拟计算值总体稍大于水工物理模型试验值,这主要是由于数值模拟中多采用理想条件计算,忽略水槽模型底部以及边壁流体撞击损失,忽略了摩擦阻力对于水流的影响。 图4 各监测点水工模型和数值模拟涌浪高度对比Fig.4 Comparison of surge height between hydraulic model and numerical simulation at each monitoring point 数值模拟可以直观的显示涌浪在弯曲河道中的传播过程,且与水工物理模型试验的涌浪高度变化过程基本一致,数值上有一定误差,可为弯曲河道传播过程研究提供参考。 根据水工物理模型试验模拟内容:用控制变量法进行多次物理试验后,得出该物理模型试验最主要的影响因素从大到小有:水深、滑块入水角度等,则三维数值模拟主要从水深和滑块入水角度两个方面进行验证水工物理模型的准确性。 水工物理模型试验并没有研究水深和滑块入水角度对坝前的涌浪高度的变化规律。通过改变河道水深和滑块下滑坡度来研究坝前涌浪变化规律。分析坝前水位变化得到滑坡涌浪对大坝最危险的工况。 3.4.1 滑坡体角度对坝前涌浪过程影响分析 研究同水深不同入水角度对于坝前水位的影响,以初始水位为0.7 m,入射角度分别为40°、50°、60°、70°、80°来探究滑坡涌浪的水位变化规律。不同角度坝前水位随时间变化如图5所示(涌浪到达坝前为计时点)。 图5 不同角度坝前涌浪高度随时间的变化线Fig.5 Variation line of swell height with time in front of the dam at different angles 通过对比分析不同角度坝前水位随时间的变化线可以得出以下规律和结论:①可以发现不同滑块下滑角度产生涌浪传播到重力坝前,坝前水位线随着时间变化的规律大体上是相似的。涌浪到达坝前,大量水体堆积处形成驻波,迅速抬高坝前水域高度,滑坡涌浪迅速达到峰值。在2 s时涌浪达到最大值。涌浪受到重力坝的阻碍在坝前引起爬高,受大坝反射,坝前水体与后续传来的水体的动能和冲击波出现振荡撞击,使得坝前水面处的动能和水面以下的冲击波波能不断发生转化,当后续能量消散后,水面开始恢复静止。通过分析可知:初始水体的动能和冲击波能最大,涌浪的爬高最大。②坝前水位的变化与滑坡体下落角度之间不是线性关系,引起坝前水位最大的工况是滑块下滑角度为60°,该工况下坝前涌浪的最大波高0.718 m,最深波谷为 0.678 m。 3.4.2 初始水位对坝前涌浪过程影响分析 由滑块角度对坝前涌浪过程影响分析可知以60°为入射角所产生的坝前波高最大,则以60°为入射角,坝前水深为0.5、0.6、0.7、0.8 m不同水深条件下滑坡涌浪对于坝前水位的影响(涌浪到达坝前为记时点)。 由不同水深坝前水位随时间的变化线(图6)可以看出坝前水位在这4种工况下,当涌浪传播到坝前时受到大坝的阻挡,然后随之产生一个驻波,坝前涌浪爬高也最大,这几种工况产生最大波峰的时间点比较接近。其中初始水位0.7 m时,坝前爬高最大,为0.016 m。在产生最大波峰后,后续水位变化规律就相差较大。产生这种情况的原因是当水槽内的初始水位较低时,滑坡体下落产生的机械能大部分会消耗在撞击河床上,所以只有一小部分的机械能转化成水体的能量,所以当初始水位较低时,涌浪传播到坝前产生的爬高较小。当水槽内的初始水位过高时,滑块机械能将全部转化为水体能量,水体体积过大将会稀释滑块机械能量,坝前波高又会降低。故最危险工况为初始水位为0.7 m,入射角为60°。 图6 不同水深坝前涌浪高度随时间的变化线Fig.6 Variation line of swell height with time in front of dam with different water depths 大坝承受的水压力由静水压力和涌浪形成的动水压力组成。根据Flow-3D软件数值模拟的计算结果,分析最危险工况的动水压强随着浪高变化的分布规律。当涌浪传播到坝前,造成坝前水面的大幅度波动,从而引起坝前动水压力的不断变化。通过观察数据可知涌浪的动水压力ΔP与涌浪高度η的关系密切,所以将动水压力换算成动水头Δh=ΔPy,y=1/(ρg)。 由最危险工况下坝前动水头与涌浪高度数值模拟结果随时间变化(图7)可以看出动水头和涌浪高度随时间变化规律。动水头和涌浪高低的变化规律和波动性基本一致,随着坝前涌浪高度的增加,其动水头也逐渐增加,波峰时产生的动水头最大。在涌浪波峰时动水头高度小于涌浪高度,在波谷时动水头高度大于涌浪高度。 图7 坝前动水头与涌浪高度数值模拟结果随时间变化Fig.7 Time-histories of simulated dynamic water head in front of dam and surge height 从各波峰时段折减系数数值模拟结果随时间的变化曲线(图8)可以得到以下几点结论:①这3个时段中t=5 s时,坝前涌浪的折减系数最大,t=7 s时折减系数最小,而t=2 s时的折减系数介于两者之间,这说明在t=2 s时,涌浪刚传播到坝前,此时涌浪相互作用相对较小;而t=5 s时,涌浪波动作用较剧烈,而坝前水位和动水头差值较大;当t=7 s时,折损系数最小,说明涌浪的能量在前一段时间的折减较大,此时涌浪的高度也相对较小,折减系数随坝前水位降低而变小。② 3个时段的折损系数分布规律类似,都随着坝前水位的减小先增加后减小,上述分析可知坝前动水头沿着水深分布有着一定程度的折减,所以当直接采用涌浪水面的静水头作为大坝水压力计算时,结果更加安全。 图8 坝前折减系数数值模拟结果随坝高分布Fig.8 Numerical results of change of reduction coefficient in front of dam with dam height 某高坝库区滑坡区位于大坝上游约1 300 m。岸坡为向河床突出的山梁,下游河流为60°折角型河流。岸坡岩体为花岗岩,滑坡范围位于两沟之间。滑坡前缘高程206 m,后缘高程292 m,相对高差86 m,坡角在30°~60°之间。发生滑坡时,坝前为蓄水时期,水位高程206.2 m,河谷呈“U”型,平均水深70 m,河道宽度约为400 m。滑坡体厚度为30~40 m,崩滑体长度约为60 m。滑坡速度约为15 m/s。 根据滑坡体与大坝位置示意图(图9)可以看出实际滑坡涌浪传播与本模型极为相似,故为了让数值模型更加符合实际模型,同时为了更好地观察和分析数据,将采用实际尺寸的弯曲河道模型进行三维数值模拟。由于某高坝实际初始水位和滑块尺寸的数据均比水工物理模型试验对应的三维数值模型数据扩大了约100倍,故将三维数值模型进行100倍扩大。根据实际滑坡数据,研究滑块体在下滑角度=50°的工况下,初始水位为70 m,滑坡体入水速度取15 m/s。滑块体的体积取60 m×30 m×30 m,根据实际山体表层平均材料密度为1 900 kg/m3,认为滑坡体在下滑过程中为刚体运动且只受重力作用,不发生变形和破坏,重力加速度为9.81 m/s2,不考虑空气阻力,时间步长为0.1 s,计算时间为50 s,通过数值模拟可以获得以初始水位70 m相对应监测点M′1、M′2、M′3、M′4(与图2监测点位置相同)位置的涌浪高度和水位变化情况。 图9 滑坡体与大坝位置示意图Fig.9 Schematic diagram of the location of landslide body and building 由图10各监测点M′1、M′2、M′3水位与试验数值模型初始水位为0.7 m、入射角为50°相对应监测点M1、M2、M3水位起伏变化规律基本一致,而监测点M′4与M4略有不同,工程实例数值模拟监测水位相比于试验数值模拟监测水位起伏频率偏大。 图10 各监测点涌浪高度数值模拟结果Fig.10 Simulated surge height at each monitoring point 由初始水位70 m相对位置的坝前涌浪高度及坝前动水头(图11)可知,随着涌浪高度的增大动水头也随之增加,波峰时产生的动水头最大。坝前涌浪波动效果与水工物理模型初始水位为0.7 m,入射角为50°的水位波动效果略有不同,但动水头波动规律基本一致。 图11 坝前动水头与涌浪高度随时间变化Fig.11 Variations of moving water head in front of dam and surge height with time 由数值模拟结果中获取在波峰时(t=10、22、40 s)折减系数沿大坝高程情况如图12所示。 图12 坝前折减系数随坝高分布Fig.12 Change of reduction coefficient in front of dam with dam height 由于水工物理模型尺寸过小,涌浪波动频率过高则折减系数明显高于实际尺寸模型折减系数,但是两次折减系数沿高程分布规律基本一致,折减系数都是随高程的降低先增后减。 本文基于库岸滑坡涌浪首浪高度试验研究,基于Flow-3D模拟技术,得出以下3点结论。 (1)数值模拟涌浪高度、水面高度起伏过程和物理模型试验结果相符。因为数值模拟多采用理想条件计算,导致数值上有少许误差,但是数值模拟还是能很好反映涌浪传播过程与大坝相互作用的过程 (2)通过滑坡体下滑的角度变化以及模型水槽的水深这两个变量的影响比较大,以0.7 m相同水深不同入射角和以相同入射角60°不同水位分析研究。最后分析得出:水深0.7 m、下滑角度60°的工况计算得出涌浪对坝体作用效应最明显。 (3)通过工程实例的验证分析得出:滑坡涌浪形成的动水头与涌浪高度和波动频率有关,涌浪高度和动水头的波动性基本一致。波峰时形成的动水头最大,动水头沿大坝高程分布有一定的折减,折减系数随坝高均为先增后减。因此采用最大涌浪爬高水头压力计算分析坝体稳定应力,其结果偏安全。3.2 三维滑坡涌浪数值模型

3.3 滑坡涌浪在弯曲河道中传播过程分析
3.4 不同因素对坝前涌浪过程的影响分析
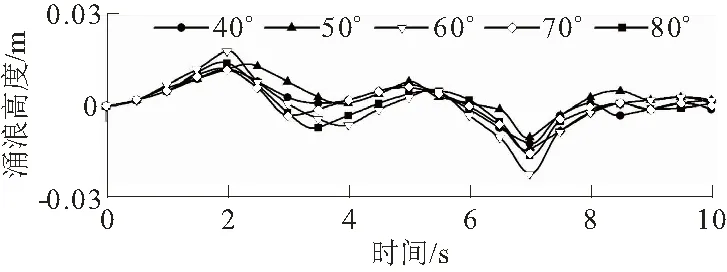
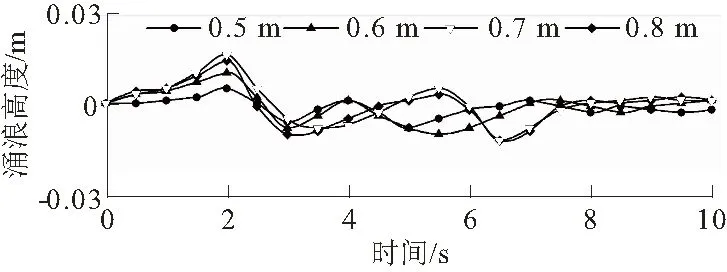
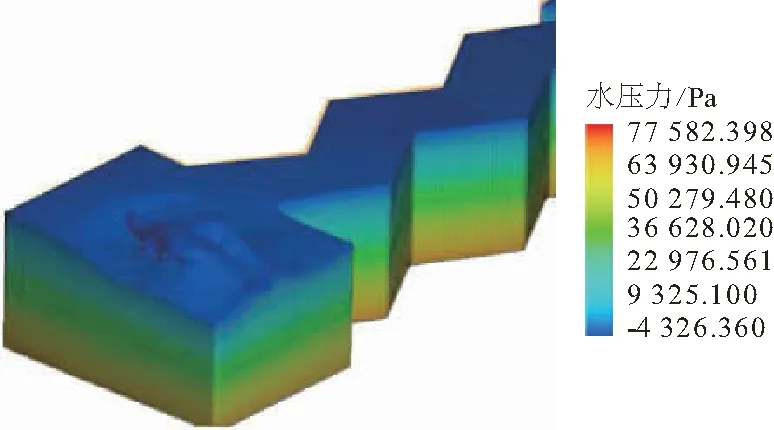
3.5 滑坡涌浪对坝体动水压力作用分析
4 工程实例



5 结 论

