大坝变形的XGBoost-LSTM变权组合预测模型及应用
邓思源,周兰庭,王 飞,柳志坤
(1.河海大学 水利水电学院, 南京 210098; 2.江苏省太湖水利规划设计研究院有限公司 设计分院,江苏 苏州 215103;3.青岛市发展和改革委员会 动能转换推进处,山东 青岛 266000; 4.青岛市经济发展研究院,山东 青岛 266000)
1 研究背景
我国目前已建有众多大坝,部分大坝在产生社会经济效益时,带来了一定安全问题,制约着工程效益的发挥,甚至威胁人民生命财产安全[1]。因此,对大坝进行可靠、高效的安全监控变得更重要,而对大坝变形发展的准确预报是整个监控过程的重要一环。
针对上述问题,相关学者提出了众多分析方法。张永光等[2]将灰色系统理论用于分析小浪底水利枢纽大坝坝顶某测点处未来变形,验证了该理论在变形预测应用中的可行性;周洪波[3]将人工神经网络用于大坝安全监控领域的研究,利用加以优化的反向传播神经网络(Back Propagation,BP),达到了较为理想的变形预测效果;任秋兵等[4]将长短期记忆神经网络(Long Short-Term Memory,LSTM)用于大坝变形预测,并通过优化算法实现了LSTM在多种典型应用场景下的更高精度的变形预测等。然而,上述研究仅局限于对难以全面分析多因素影响的单一预测模型的构建和优化,未充分考虑多方面不确定因素对大坝变形的影响,预测精度有待进一步提高。
为探求更高性能的预测方法,相关学者又试图将多个单一模型进行组合用以预测大坝未来变形。杨恒等[5]构建了一种支持向量机(Support Vector Machine,SVM)和差分自回归移动平均模型(Auto-regressive Integrated Moving Average,ARIMA)相结合的大坝变形预测模型;马佳佳等[6]将长短期记忆神经网络(LSTM)与多元线性回归(Multiple Linear Regression,MLR)通过引入集合经验模态分解(Ensemble Empirical Mode Decomposition,EEMD)方法进行结合;周兰庭等[7]将LSTM和ARIMA通过引入小波分析(Wavelet Analysis,WA)方法进行结合等,均取得了较单一模型更好的预测效果。然而,现有的类似于上述组合模型的研究都只是对各单一模型的预测结果的简单相加,或者将模型A的预测结果简单输入到模型B中的二次预测等,一定程度上呈现出一种“机械组合”的特征,没有充分实现组合模型间的灵活结合[8]。
基于上述问题,本文引入了一种在残差赋权的基础上加以改进的自适应赋权的变权组合方法[9],它既非单一模型的“简单相加”,也非模型A到模型B的“二次预测”。鉴于极端梯度提升算法(eXtreme Gradient Boosting,XGBoost)[10]和长短期记忆神经网络(LSTM)[11]对于非线性非平稳且时序性强的数据均具有较高的预测精度,且二者方法原理相差较大而使得预测结果相关性较低,有利于对监测样本数据中有用信息的充分挖掘和利用,本文选用XGBoost模型和LSTM模型进行变权组合,提出一种大坝变形的XGBoost-LSTM变权组合预测模型,以期实现更为准确可靠的大坝变形预测。
2 研究方法
2.1 极端梯度提升算法(XGBoost)
XGBoost算法是在梯度提升树(Gradient Boosting Decision Tree,GBDT)的基础上加以改进的一种集成学习算法,其核心理念在于将弱分类器集成为一个强分类器[12],即将上一步弱学习器训练的残差通过引入新的弱学习器加以拟合,当训练结束后会产生每一样本对应的预测分数,通过对全部弱学习器产生的预测分数求和即可得到最终的样本预测值。
XGBoost的结构如图1所示。

图1 XGBoost结构示意图Fig.1 Schematic diagram of XGBoost structure
对于某变形测点,假设其具有n个样本,且每个样本具有m个特征值,将其监测资料用M={(xi,yi)}(xi∈Rm,yi∈R,i=1,2,…,n)表示。XGBoost采用CART(Classification and Regression Tree,分类回归树)模型作为弱学习器[13],对于第i个样本的预测,其预测函数为
(1)

在模型的训练过程中,将目标函数定义为
(2)
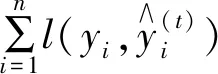
对式(2)中的损失函数泰勒二阶展开,则可近似求得目标函数为
(3)
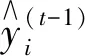
在XGBoost算法中,对于单棵决策树的复杂度,可由式(4)计算,即
(4)
式中:T和γ分别代表叶子节点的数量及其数量的惩罚项;wk代表第k个节点的分数;λ代表L2正则惩罚项,L2代表欧氏距离。
基于式(4)即可得到由t棵树构成的复杂度函数,即
(5)
式中const为一常量,代表前t-1棵树的复杂度的总和。
鉴于优化函数的过程中常数项不会造成影响,则目标函数经过t次迭代后可简化为
(6)
2.2 长短期记忆神经网络(LSTM)
长短期记忆神经网络(LSTM)[14]是对循环神经网络(Recurrent Neural Network,RNN)的一种改进。与传统的RNN相比,LSTM在其网络中的每个记忆神经元上均新添了一个记忆单元状态以降低信息丢失速度,同时其3个门结构(即遗忘门、输入门和输出门)用以对梯度下降时误差函数反馈的修正参数进行选择性记忆。LSTM通过引入可控自循环巧妙规避了RNN在长时间序列学习过程中易产生的梯度消失或梯度爆炸问题,对于处理时序延迟和间隔冗长的任务效果显著。其单元内部结构如图2所示。

图2 LSTM单元内部结构Fig.2 Internal structure of LSTM unit
LSTM的主体运行步骤如下:
(1)通过遗忘门控制前一单元输入信息的被遗忘程度,筛选并保留历史信息中有价值的部分。
具体计算式为
ut=σ(Whuht-1+WxuXt+bu) 。
(7)
式中:ut代表遗忘门限;ht-1和Whu分别代表隐含层前一时刻的输出和权重矩阵;Xt和Wxu分别代表隐含层当前时刻的输入和权重矩阵;bu代表偏置值向量;σ代表标准sigmoid激活函数。
(2)通过输入门控制流入到单元中的信息量,尽可能地将更高的权重分配给更有价值的信息,以此来更新单元状态。
具体计算式为
it=σ(Whiht-1+WxiXt+bi) ;
(8)
(9)
(10)

(3)通过输出门决定最终的输出信息。
具体计算式为
ot=σ(Whoht-1+WxoXt+bo) ,
(11)
ht=ottanh(Ct) 。
(12)
式中:ot代表输出门限;Who和Wxo分别代表前一时刻和当前时刻的权重矩阵;bo代表偏置值向量。
(4)采用误差反向传播算法对模型多次训练,以达到期望的模型指标。
2.3 随机森林模型、ELMAN模型与逐步回归分析模型
本文分别引入随机森林模型与ELMAN模型作为后文实例应用分析中模型之间的对比依据,以期验证XGBoost和LSTM两种模型在各自领域的优越性;同时,加入较为传统的逐步回归分析模型进行对比研究,以进一步说明本文模型的先进性。
随机森林模型是一种基于决策树(分类回归树)建立的集成学习算法,适用于处理大坝变形数据分析这类存在复杂交互作用或非线性关系的问题。决策树采用一种二分递归分割方法,遵照既定规则,对样本集进行分割以形成2个子样本集。除了叶节点,决策树各节点拥有2个分支,再依循上述过程,采用递归方式对每个分割后的子集进行反复分割,以不可再分为叶节点为限。随机森林运用Bagging算法进行决策树的组合,实质上是一个包含一系列决策树的分类器。其具体介绍及算法流程参见文献[15],本文不再详述。
ELMAN模型是一种动态的反馈神经网络模型,由普通的输入层、隐含层和输出层以及一个特殊的隐含层(上下文层或状态层)组成。输入层和输出层两单元分别具备信号传输和线性加权的功能,可将激活函数作用于隐含层单元。状态层单元则负责对隐含层单元上一时刻的输出值进行记忆,接收并处理由隐含层得到的反馈信号。若ELMAN网络通过正切S形隐层和纯线性输出层构成,则可对任一连续函数进行逼近。具备反馈连接的ELMAN网络可生成2种模式,即时间模式和空间模式。ELMAN神经网络仅需运用系统给出的输入和输出数据,即可实现对系统的模型构建,此外还能使效应量与影响因子间的非线性关系得以体现。其具体介绍及建模分析流程参见文献[16],本文不再详述。
逐步回归分析模型是一种可自主通过在众多变量中寻得最有价值变量,进而构建回归分析预测或解释的模型。相较于普通的多元回归方法,逐步回归的优越性在于其剩余标准差更小,方程更稳定,从而确保方程中的全部回归因子均具备显著性[17]。其具体介绍及建模分析流程详见文献[18],本文不再详述。
2.4 组合预测方法
组合预测方法在预测科学中的应用较为广泛,其理论认为:针对同一预测问题,将多种不同的预测模型进行有机结合可在一定程度上提升模型的拟合能力,进而实现更好的预测效果[19]。组合模型的预测效果与各单一模型权值的分配有密切关联,这就涉及到对赋权方法的合理使用。常用的赋权方法有固定赋权和自适应赋权,固定赋权又可细分为等值赋权和残差赋权。
本文对于固定赋权方法不再赘述,而是主要阐述一种在残差赋权的基础上加以改进的自适应赋权的变权组合方法,其通过以下步骤进行实现。
(1)将组合模型的预测残差平方和作为目标函数以得到组合预测优化模型,即

式中:eit代表t时刻第i种模型的拟合残差;vit代表t时刻第i种模型的权值;n代表单一模型的种数;m代表实测样本点的数量。
通过解算该组合预测优化模型,即可得到各模型在各样本点处的最优权值vit,进而实现组合预测模型拟合精度的最优化。
(2)为了达到预测的目的,根据上述求得的各样本点处的最优权值vit,推求各预测点处的最优权值vi,m+j(i=1,2,…,n;j=1,2,…)(j代表预测点的数据),常用方法有以下2种。
第一种:适用于样本量较少或者各模型在时点序列处的权值无明显规律的情况,其推算过程为
第二种:适用于样本量较多且各模型在时序点处的权值存在一定规律的情况,其核心思想在于采用回归法拟合权值函数,再以此为依据计算各预测点的组合预测权值。然而,由于大坝变形监测数据的特殊性,各模型在时点序列处的权值不存在明显规律,此种方法难以适用于大坝变形分析预测,故本文对该方法不再赘述。
根据以上内容不难得出,变权组合方法的基本思路在于,采用某种最优化原则对各单一模型在样本点处的组合权值进行求解调配,再利用经过上述过程处理得到的组合权值,尽可能地寻求各模型每一预测点处预测值的最优权占比。换言之就是通过一种各模型权值不断滚动优化的过程,或者通过一种权值与时间对应的最优函数关系,实现概率意义上的更高精度的预测[20]。
2.5 XGBoost-LSTM变权组合预测模型
鉴于XGBoost模型和LSTM模型对于处理大坝变形序列这种具有较强时序性和非线性特征的数据的优越性和先进性,同时分别作为树模型和神经网络模型,其原理具有较大的差异性而使得模型运行结果的相关性较弱,将二者融合有利于提升预测的准确度[21],本文引入XGBoost和LSTM作为组合模型的构成部分;此外,考虑到大坝变形序列具有典型的非线性和非平稳性,且监测样本序列和各模型预测效果可能随时间而不断改变,本文采用上述变权组合方法进行XGBoost和LSTM的有机组合,同时由于各模型在时点序列处的权值不具有明显规律性,选用2.4节实现过程中步骤(2)谈及的第一种方法。综上所述,本文基于融合建模的思想,引入变权组合方法,将XGBoost模型和LSTM模型进行有机融合,提出一种大坝变形的XGBoost-LSTM变权组合预测模型,以期实现预报精度的进一步提升。
其主体实现步骤概述如下:
(1)在数据预处理的基础上,分别进行XGBoost模型与LSTM模型的建模分析预测,获得各单一模型的分析预测结果。
(2)根据步骤(1)得到的各模型预测结果,采用上述变权组合方法拟定各单一模型的权值,进而推求组合模型的最终预测结果。
(3)引入评价指标进行模型评价,以期验证各单一模型以及组合模型的预测效果。
其建模分析主体流程如图3所示。
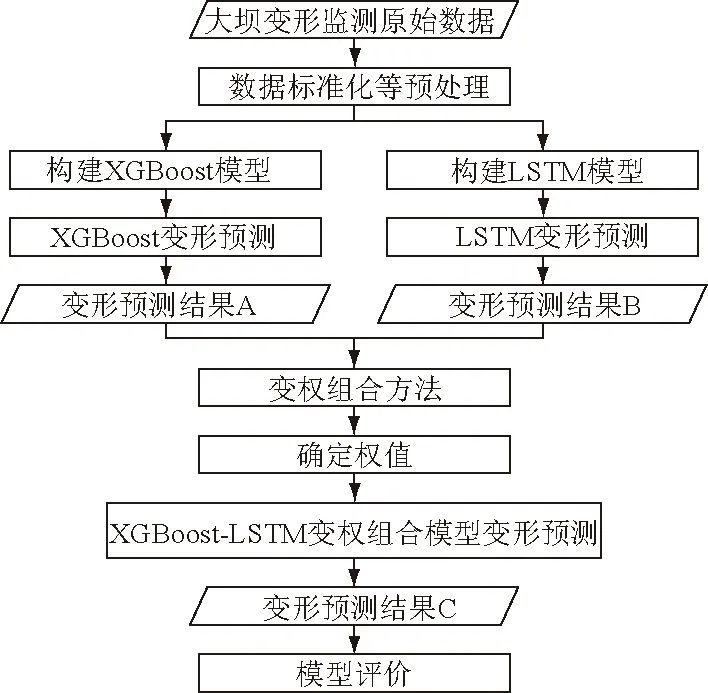
图3 XGBoost-LSTM变权组合预测模型建模分析主体流程Fig.3 Flow chart of modeling and analysis of XGBoost-LSTM combinatorial model with variable weight
3 实例应用
3.1 实例概况
本文选用某混凝土
重力坝作为研究对象,截取该坝10#坝段的引张线测点EX8处2013年1月1日到2013年12月31日的365个变形观测样本数据进行分析,以说明本文方法思路的可行性和优越性。其变形过程线见图4。

图4 变形过程线Fig.4 Process line of deformation
3.2 建模分析与评价
根据前文论述的理论方法将上述365个样本数据中的前350个数据划作训练集,后15个数据划作测试集,进行XGBoost-LSTM变权组合预测模型的建模分析预测。为了验证本文单一模型及其组合模型的预测效果,选用XGBoost模型、LSTM模型、随机森林模型、ELMAN模型、逐步回归分析模型以及XGBoost-LSTM等值赋权组合预测模型在同一条件下进行对比实验。
本文将均方根误差(Root Mean Square Error,RMSE)作为各模型的评价指标,其计算公式为
(14)
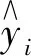
3.2.1 单一模型建模分析与评价
鉴于组合模型的预测性能很大程度上与构成其本身的各单一模型的预测性能有关,本文首先对各单一模型进行建模分析与评价,以验证其在各自模型类别的优越性和大坝变形预测方面的适用性。
3.2.1.1 XGBoost模型、随机森林模型与逐步回归分析模型的建模预测及对比分析
XGBoost模型和随机森林模型均是当下较为成熟的树模型,作为Boosting算法和Bagging算法的典型代表,在预测科学领域都取得了一定的成功;此外,逐步回归分析模型作为时下较为传统的回归分析模型,在相关领域得到了较为成熟且广泛的应用,具有深刻的对比研究价值。因此,本文基于上述数据集和数据划分,首先进行XGBoost模型、随机森林模型与逐步回归分析模型的建模预测及对比分析。
本文主要参考文献[22],利用Python3.7中的XGBoost库构建XGBoost大坝变形预测模型,将大坝变形的影响因子(包括水压因子、温度因子以及时效因子)作为输入变量,输出变量则为该测点处变形,同时采用Scikit-learn中的网格搜索法进行超参数寻优。其主要参数设置结果见表1,其余参数采用默认值。

表1 XGBoost模型参数设置结果Table 1 Parameter settings of XGBoost model
对于随机森林模型的参数设置和建模应用主要参考文献[15]和文献[23],其主要参数设置结果见表2,其余参数采用默认值。

表2 随机森林模型参数设置结果Table 2 Parameter settings of random forest model
本文主要参考文献[18],通过寻求最优因子组合,将水压因子、温度因子和时效因子作为因子集,进行逐步回归分析模型的构建及应用。
各模型预测结果对比见图5,各模型评价指标对比见表3。

图5 XGBoost模型、随机森林模型与逐步回归分析模型预测结果对比Fig.5 Comparison of prediction results among XGBoost model,random forest model and stepwise regression analysis model

表3 XGBoost模型、随机森林模型与逐步回归分析模型评价指标Table 3 Evaluation indicators of XGBoost model,random forest model and stepwise regression analysis model
由图5可见,XGBoost模型和随机森林模型二者的变化趋势相较于传统的逐步回归分析模型更加趋向真实值;又由表3可得,逐步回归分析模型的预测均方根误差RMSE为0.423 9 mm,大于随机森林模型的0.328 8 mm和XGBoost模型的0.233 9 mm;综上所述,XGBoost和随机森林两种树模型的预测性能均优于传统的逐步回归分析模型,具有一定的先进性;进一步地,对两种树模型进行对比分析,同样由图5可见,虽然随机森林模型在本次实验中后半段的预测效果略微优于XGBoost模型,但是前半段的预测精度却明显低于XGBoost模型,导致其整体预测精度不佳,换言之,从总体来看,XGBoost模型的预测过程线相较于随机森林模型与实测过程线更为贴合,整体表现更加稳定;再由表3可得,XGBoost模型的预测均方根误差RMSE为0.233 9 mm,低于随机森林模型的0.328 8 mm,进一步证明了XGBoost模型的预测精度高于随机森林模型,更适用于大坝变形预测。因此,本文将XGBoost模型用于组合模型的构成模型之一。
3.2.1.2 LSTM模型、ELMAN模型与逐步回归分析模型的建模预测及对比分析
LSTM模型作为时下较为先进的神经网络模型已在大坝安全监控领域取得了一定的成功,ELMAN模型作为一种传统递归神经网络模型也较为成熟地被应用于相关领域的研究。因此,基于上述数据集和数据划分,本文再对LSTM模型和ELMAN模型进行建模预测及对比分析;出于相同考虑,引入前文逐步回归分析模型的分析预测成果进行对比研究。
本文主要参考文献[24]进行LSTM模型的构建和超参数设置,参数寻优采用Adam算法[25],其主要参数设置结果如表4所示,其余参数采用默认值。

表4 LSTM模型参数设置结果Table 4 Parameter settings of LSTM model
对于ELMAN模型的参数设置和建模应用主要参考文献[16],通过试算法将与模型预测精度密切相关的网络隐含层节点数拟定为3,其余参数采用参考值和默认值。
各模型预测结果对比见图6,各模型评价指标对比见表5。

图6 LSTM模型、ELMAN模型与逐步回归分析模型预测结果对比Fig.6 Comparison of prediction results among LSTM model,ELMAN model and stepwise regression analysis model

表5 LSTM模型、ELMAN模型与逐步回归分析模型评价指标Table 5 Evaluation indicators of LSTM model,ELMAN model and stepwise regression analysis model
由图6可见,LSTM模型和ELMAN模型二者的预测曲线走势相较于传统的逐步回归分析模型更加贴合真实值,且由表5可得,LSTM模型和ELMAN模型的预测均方根误差RMSE分别为0.107 6 mm和0.210 4 mm,均小于逐步回归分析模型的0.423 9 mm;综上所述,LSTM和ELMAN两种神经网络模型均表现出比逐步回归分析模型更高的预测性能,具有一定的优越性;进一步地,对两种神经网络模型进行比较分析,同样由图6可见,LSTM模型的变形预测值显然比ELMAN模型更加贴合测点变形真实值,且各点走势更加符合真实值变化规律,与工程实际情况更为吻合,肉眼可见其预测效果更优;同时,由表5得到,LSTM模型的评价指标RMSE为0.107 6 mm,小于ELMAN模型的0.210 4 mm,进一步说明了LSTM模型相较于ELMAN模型具有更高的预测精度,在大坝变形监测领域优势更加显著。因此,本文选择预测表现更优的LSTM模型作为组合模型的构成模型之一。

图7 XGBoost模型、LSTM模型、等值赋权组合模型、变权组合模型预测结果对比Fig.7 Comparison of prediction results among XGBoost model,LSTM model,equal-weighted combination model,and variable-weighted combination model
3.2.2 组合模型建模分析与评价
综上所述,基于XGBoost模型和LSTM模型,采用前文谈及的自适应赋权的变权组合方法进行组合预测模型的构建,最后,基于同样的数据集和数据划分,进行变形分析预测。为了验证本文变权组合模型的预测性能,将XGBoost模型、LSTM模型、XGBoost-LSTM等值赋权组合预测模型与XGBoost-LSTM变权组合预测模型的预测结果进行对比分析。各模型预测结果对比见图7,各模型评价指标对比见表6。

表6 XGBoost模型、LSTM模型、等值赋权组合模型、变权组合模型评价指标Table 6 Evaluation indicators of XGBoost model,LSTM model,equal-weighted combination model,and variable-weighted combination model
由图7可见,XGBoost-LSTM等值赋权组合预测模型的预测过程线的波动范围相较于XGBoost模型与LSTM模型更加贴合真实值,基本能更加准确地反映真实值变化趋势,预测效果得到一定程度的提升,但不足之处在于其权值固定导致赋权之后一些细节信息的丢失,不能更加真实地反映工程实际情况;而反观XGBoost-LSTM变权组合预测模型,其预测结果过程线与真实值的吻合程度相较于XGBoost-LSTM等值赋权组合预测模型又有了一定程度的提升,每点处预测值都尽可能地逼近真实值,预测精度改善明显。同时,XGBoost-LSTM变权组合预测模型更大程度地保留了细节信息,更能从定量而非定性的层面反映大坝变形趋势和工程实际情况,预测效果更为理想。此外,表6中的各模型评价指标也进一步验证了上述内容,将表6中的均方根误差RMSE从小到大依次排列:变权组合预测模型的0.040 0 mm<等值赋权组合预测模型的0.083 3 mm 综上所述,XGBoost-LSTM变权组合预测模型相较于其余3种预测模型具有更好的预测效果,预测结果更加符合工程实际情况,在大坝变形预测中具有一定的优势和可研究价值。 本文鉴于XGBoost作为树模型在预测科学领域的先进性以及LSTM作为神经网络模型在分析时间序列方面的优越性,应用变权组合预测方法将上述2种模型进行有机融合,构建了一种XGBoost-LSTM变权组合预测模型,并将其用于大坝变形预测。实例应用表明,与传统的逐步回归分析模型比较,XGBoost和随机森林2种树模型以及LSTM和ELMAN这2两种神经网络模型在大坝变形预测中均表现出更好的预测效果,具有一定的先进性;而相较于同为树模型的随机森林模型,XGBoost模型预测性能更加稳定和优越;与同为神经网络模型的ELMAN模型相比,LSTM模型则具有更优的预测表现;进一步地,基于变权组合方法将XGBoost和LSTM进行有机融合可以优化各单一模型的预测性能,且相较于基于等值赋权方法的XGBoost和LSTM的简单组合,预测精度提升更加显著,预测结果信息显示更加丰富,更加符合工程实际情况。综上所述,本文提出的大坝变形的XGBoost-LSTM变权组合预测模型在大坝安全监控领域具有一定的适用性和优越性,可进行发展和推广。4 结 论

