列车时速和轴重对脱粘支承层表面粗糙峰微凸体的影响分析

张光明 ，李威 ，刘观 ，段海滨 ，段玉振 ，陈鹏

（1.北京城建设计发展集团股份有限公司 轨道工程技术中心，北京 100037；2.北京市轨道结构工程技术研究中心，北京 100037）

0 引言

《新时代交通强国铁路先行规划纲要》指出，到2035年我国高速铁路里程将达到7万km［1］。双块式无砟轨道作为我国主要的无砟轨道类型，在我国运营高铁和城际铁路轨道中占有相当大的比重［2］。双块式无砟轨道层间接触处的新旧混凝土界面作为该型无砟轨道的受力薄弱区，极易出现离缝、粉化、上拱等多种病害［3-5］。

针对双块式无砟轨道的层间病害，通过理论［6］、试验［7］和有限元法［8］等进行了一定程度的研究，但未考虑到层间脱粘处的道床板和支承层的实际接触不存在于整个表面，仅存在部分区域，即粗糙接触，目前有关结构表面间的粗糙接触模型有统计学模型［9-15］、分形模型［16-20］和真实表面模型［21-23］等。此外混凝土作为一种非连续不均匀介质，有限元法不能反映混凝土的各向异性损伤。

考虑到现有脱粘道床板和支承层层间粗糙接触的研究较少，同时针对客货共线无砟轨道离缝发生翻浆冒泥病害较客运线路更为严重的情况，拟将有限元法和颗粒离散元法结合，得到不同车速、轴重时脱粘道床板底部的竖向位移和速度，以此探究列车时速和轴重对脱粘支承层表面粗糙峰微凸体的影响。

1 含板边离缝双块式无砟轨道模型

1.1 模型建立与参数取值

建立路基上含板边离缝的双块式无砟轨道实体模型，包括钢轨、扣件、道床板、支承层和地基等结构（见图1）。钢轨用梁单元模拟；扣件系统和地基用线性弹簧单元模拟；道床板和支承层采用实体单元模拟；板边脱粘处设置层间接触；模型全长9.75 m，共计146 370个单元、240 873个节点。

图1 含板边离缝双块式无砟轨道实体模型

将板边离缝区简化为长方形，取离缝长度为6.5 m、深度为0.9 m、高度为0.01 m。道床板和支承层的热膨胀系数为1×10-5/℃；扣件垂向刚度取39.2 kN/m［24-26］，纵向刚度取15 kN/mm，横向刚度取40 kN/mm［25］；路基地基系数取76 MPa/m［27］，摩擦系数取1.5［24］；温度梯度修正系数取0.89［24］；其余模型计算参数见表1。

表1 模型计算参数

1.2 荷载工况和边界条件

路基地段的荷载包括疲劳检算荷载和温度梯度荷载。其中疲劳检算荷载大小参照文献［28］，取客车轴重为17 t，货车轴重为23 t和25 t，温度梯度取+90℃/m，车速取150、200、250 km/h。计算工况见表2。

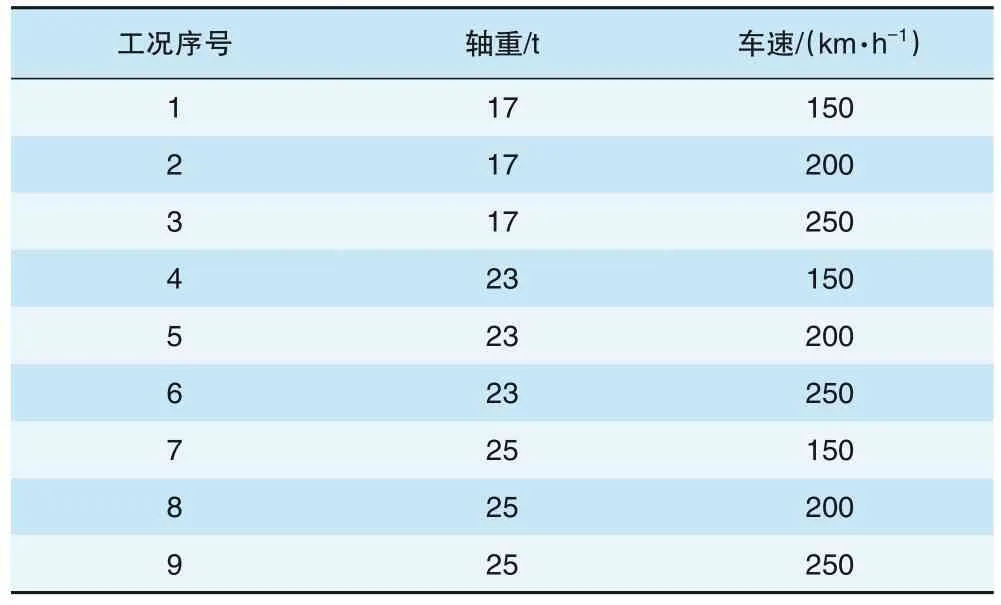
表2 计算工况

边界条件为钢轨两端全约束，地基弹簧底部全约束。

1.3 计算结果

利用有限元软件的瞬态分析模块进行计算，提取不同轴重和车速时脱粘道床板底部的最大竖向位移和竖向速度（见图2和图3）。

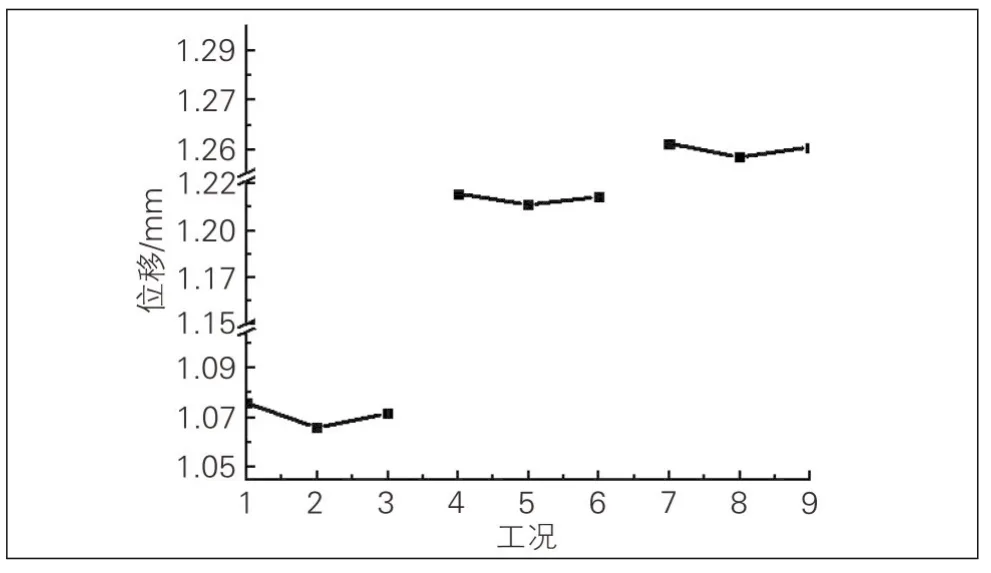
图2 不同轴重和速度下的脱粘道床板竖向位移

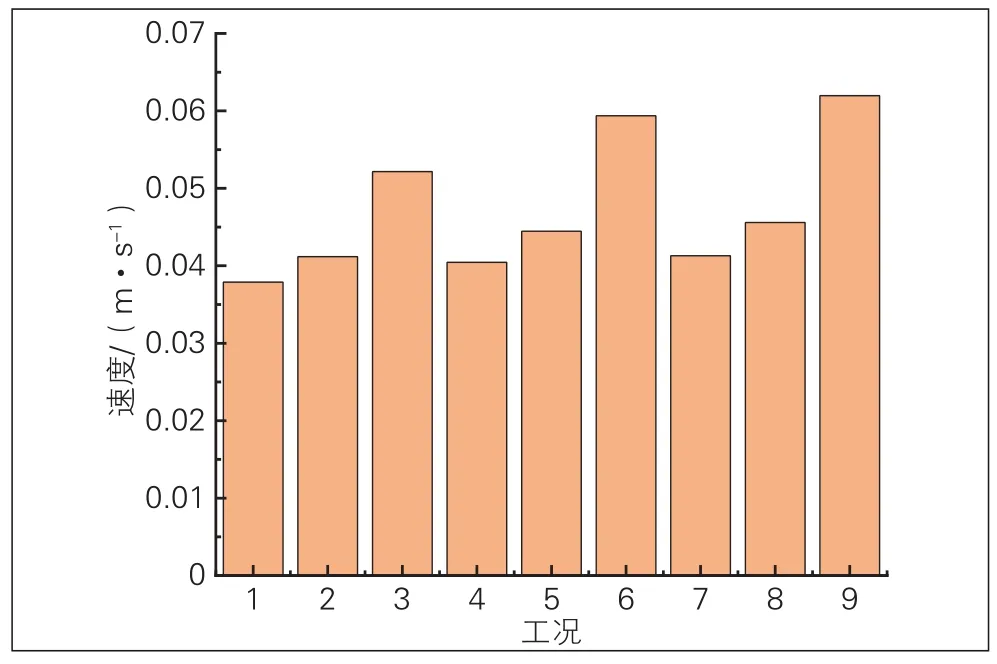
图3 不同轴重和速度下的脱粘道床板竖向速度

通过图2和图3可以看出，当轴重一定时，随着列车运行速度的增加，脱粘道床板底部竖向位移无明显增大，脱粘道床板底部竖向速度增幅明显，当列车时速从150 km/h增加至200 km/h时，其速度增幅仅为10%左右，当列车时速从200 km/h增加至250 km/h时，其速度增幅为30%左右；当速度一定时，随着轴重的增加，脱粘道床板底部竖向位移和速度均有明显增加，但轴重从17 t增加至23 t（增幅35%），脱粘道床板底部竖向位移和速度增幅仅为轴重增幅的1/5～1/3，轴重从23 t增加至25 t（增幅8.7%），脱粘道床板底部竖向位移和速度增幅仅为轴重增幅的1/4～1/2。

2 支承层表面粗糙峰微凸体离散元分析

2.1 支承层表面粗糙峰微凸体离散元模型建立

将支承层表面浮浆薄层混凝土离散成直径2.0～5.0 mm（占比30%）、1.0～2.0 mm（占比20%）、0.2～1.0 mm（占比50%）、孔隙率0.1的颗粒，建立混凝土单轴抗压试件数值模型，求得模型应力应变曲线，并与Hognestad函数求得的C15混凝土宏观应力-应变曲线对比，经过多次试算得到C15混凝土的细观参数（见表3）和应力-应变曲线（见图4）。

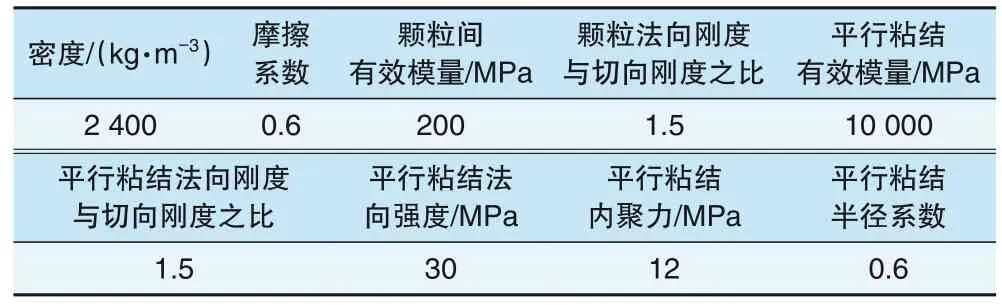
表3 C15混凝土细观参数

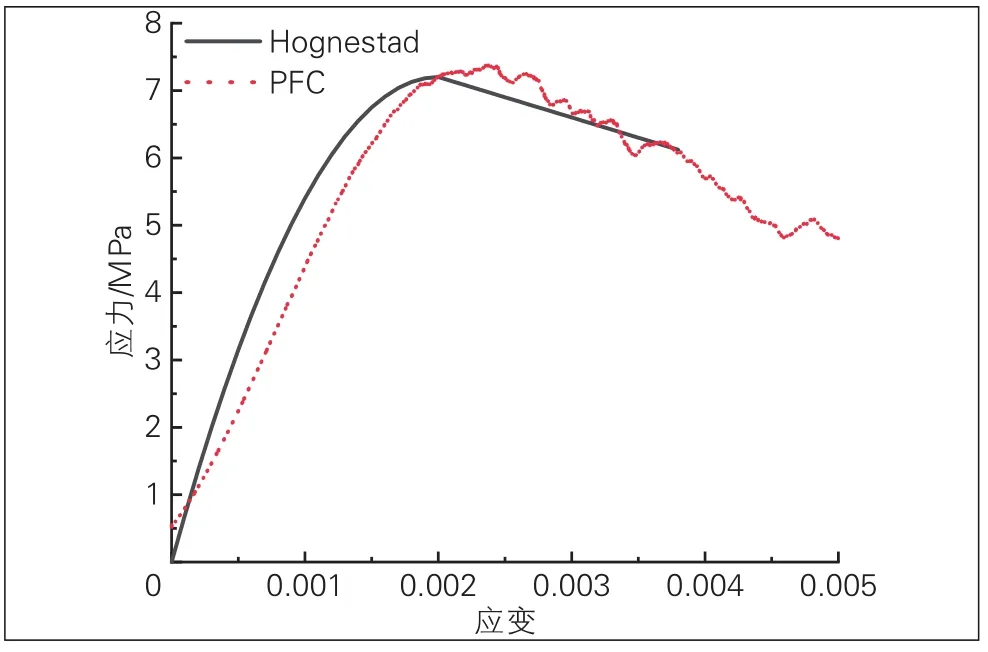
图4 C15混凝土应力-应变曲线

相关研究表明，物体之间的实际粗糙接触是微凸体之间的相互作用，因此将支承层表面粗糙峰简化为微凸体；同时考虑到粗糙峰的微观尺寸较小，若按原尺寸进行建模，模型中的颗粒尺寸较小，而参数标定时的单轴抗压支承层混凝土试件数值模型尺寸是一定的，故颗粒越小，参数标定时的颗粒越多，则标定时间越长，同时对计算机的性能要求越高。因此，将脱粘后的支承层表面粗糙峰抽象成半径为0.03 m的半圆形微凸体，利用颗粒流离散元软件建立多粗糙峰的C15支承层表面粗糙峰微凸体离散元模型，经过成样、伺服和胶结后的模型见图5，共计24 390个颗粒。

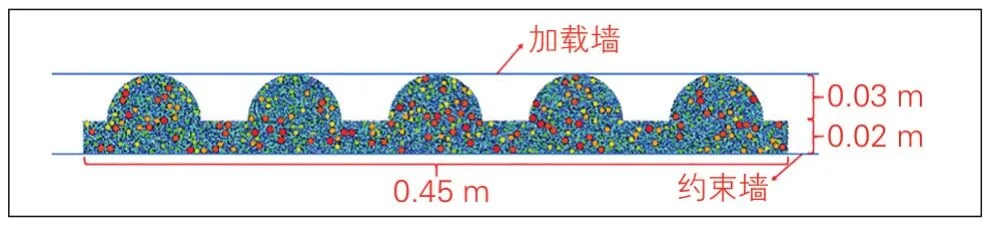
图5 支承层表面粗糙峰微凸体离散元模型

模型中颗粒之间采用线性平行粘结模型，颗粒与墙体之间采用线性接触模型，墙与颗粒之间的刚度为颗粒刚度的10倍［16］。模型边界条件为约束墙全约束，荷载条件为上部加载墙施加位移荷载。

2.2 不同列车时速的影响分析

为明确不同列车时速对支承层表面粗糙峰微凸体的影响，将轴重23 t，车速150、200、250 km/h的位移和速度结果（即工况4、5和6）施加于图5中的加载墙，支承层粗糙峰微凸体裂缝数量和长度见图6和图7。

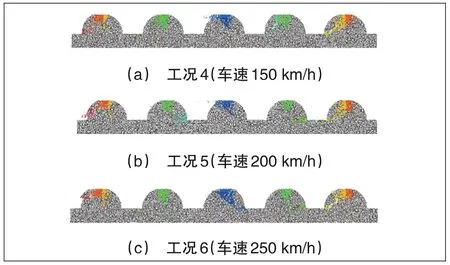
图6 轴重23 t时支承层粗糙峰微凸体裂缝产生量

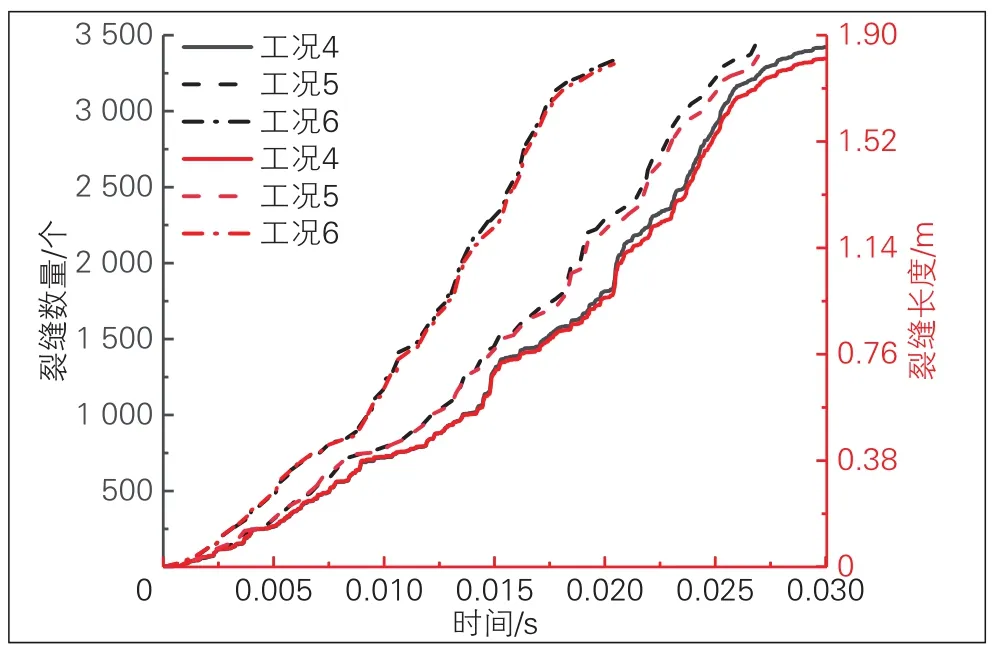
图7 轴重23 t时支承层粗糙峰微凸体裂缝数量和长度的时程曲线

通过图6和图7可以看出，裂缝数量和长度随时间的变化也基本一致，均是增幅先增大后减小。从图6（c）可以看出，时速的增加会导致微凸体裂缝不断向峰底延伸；统计可知工况4—工况6的3种车速时支承层粗糙峰微凸体裂缝数量分别为3 422、3 487、3 338个，长度分别为1.817、1.851、1.798m，与图2位移类似，基本无较大变化。

2.3 不同轴重的影响分析

为明确不同列车轴重对支承层表面粗糙峰的影响，将车速250 km/h，轴重17、23、25 t的位移和速度结果（即工况3、6和9）施加于图5中的加载墙，结果见图8和图9。

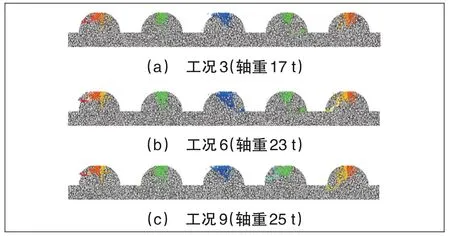
图8 车速250 km/h时支承层粗糙峰微凸体裂缝产生量

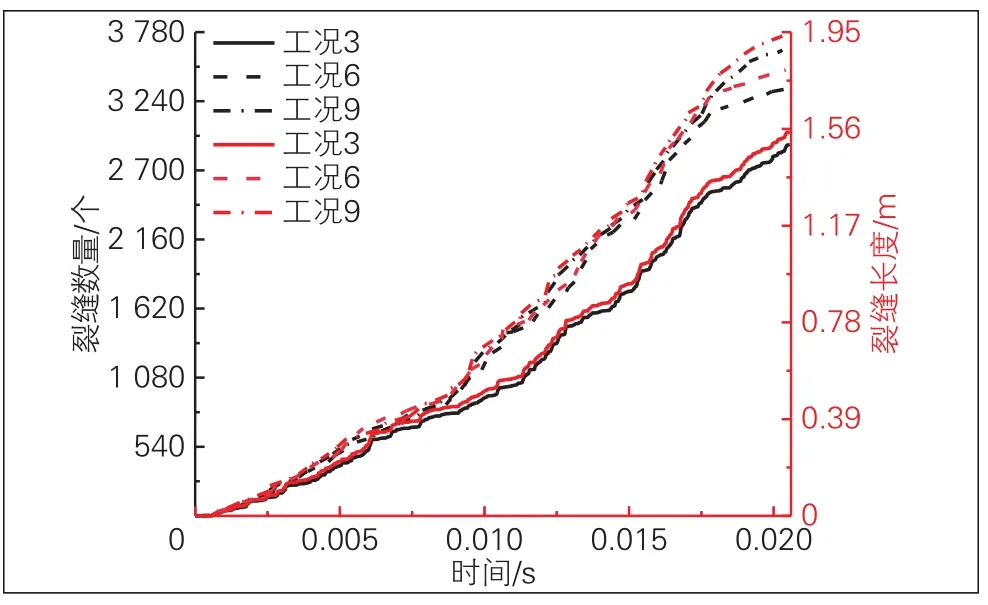
图9 车速250 km/h时支承层粗糙峰微凸体裂缝数量和长度的时程曲线

由图8和图9可知，裂缝数量和长度与轴重呈正相关，且增幅均随着时间先增大后减小。同时由图8可以看出，随着轴重的增加，支承层粗糙峰微凸体内的贯通裂缝也越来越多，即更容易导致粗糙峰微凸体上的颗粒掉落成粉（颗粒较小）。统计可知工况3、6、9的3种轴重时支承层粗糙峰微凸体裂缝数量分别为2 900、3 338、3 693个，长度分别为1.548、1.798、1.934 m。

经分析可知轴重分别从17 t增加至23 t和25 t时，对应的裂缝数量增幅分别为15.1%和27.3%，裂缝长度增幅分别为16.1%和24.9%。可以看出相较于轴重的增加（轴重增幅分别为35%和47%），虽然裂缝数量和长度增幅均小于轴重增幅，但裂缝长度和数量的增幅比分别为1.55和1.81，大于轴重的增幅比1.34，即说明随着轴重的增加，裂缝数量和长度的增加幅度会越来越大。

3 结论

将有限元法和颗粒离散元法结合，研究了列车时速和轴重对支承层表面粗糙峰微凸体的影响，主要结论如下：

（1）列车运行速度的增加，脱粘道床板底部竖向位移无明显增大，脱粘道床板底部竖向速度增幅明显，且当列车速度分别从150 km/h增加至200 km/h和从200 km/h增加至250 km/h时，脱粘道床板底部竖向位移增幅较小，但后者的竖向速度增幅是前者的3倍；

（2）脱粘道床板底部竖向位移和速度与轴重呈正相关，且增幅明显；

（3）列车运行时速的增加对裂缝数量和长度无明显影响，但会导致裂缝往峰底延伸，且裂缝数量和长度随时间的变化也基本一致，均是增幅先增大后减小；

（4）裂缝数量和长度与轴重呈正相关，且增幅均随着时间先增大后减小，同时随着轴重的增加，支承层粗糙峰微凸体内的贯通裂缝也越来越多，即更容易导致粗糙峰微凸体上的颗粒掉落成粉；

（5）相较于轴重的增加，虽然裂缝数量和长度增幅均小于轴重增幅，但两者的增幅比明显不同，裂缝长度和数量的增幅比大于轴重的增幅比，随着轴重的增加，裂缝数量和长度的增加幅度会越来越大。