自适应阶次跟踪技术在走行部故障诊断中的应用

包学海，孔繁鹏，谢烨，水沛，尹旭晔

（1.浙江杭海城际铁路有限公司 工程管理部，浙江 杭州 310000；2.中铁信（北京）网络技术研究院有限公司 技术开发部，北京 100000；3.浙江省交通投资集团有限公司 智慧交通研究分公司，浙江 杭州 310000；4.浙江中自庆安新能源技术有限公司 产品部，浙江 杭州 310000）

1 概述

城市轨道交通作为一种运能大、速度快、安全准时、能源节约、环境友好的交通方式，逐渐成为城市公共交通的骨干，是大中城市解决交通问题的首选交通方式。据中国城市轨道交通协会统计，截至2019年12月31日，我国共有40座城市开通运营轨道交通列车，运营里程合计约6 730 km。目前，城市轨道交通列车维修模式多以计划性维修为主，即按运行公里或时间间隔进行定期维护或维修。走行部作为列车重要的系统之一，其工作状态直接影响列车运行安全。针对走行部轴箱轴承、齿轮箱、电机等旋转部件，通过人工“耳听目测”检查方式难以判断出部件故障，尤其针对一些早期故障及隐患不能及时判断和预警，列车的运行安全受到严重威胁。

在变转速转子故障诊断方面，唐贵基等［1］提出一种基于SSD-HT时频阶次跟踪的转子故障诊断方法。杨炯明等［2］在阶次分析中引入瞬时频率理论，研制出虚拟式旋转机械特征分析仪。Borghesani等［3］提出一种新的基于速度同步的离散傅里叶变换，提高了计算阶次跟踪的分析效果。Wu等［4］基于递推最小二乘（RLS）滤波的阶次跟踪算法对振动信号和声发射信号进行特性分析和试验比较。Pan等［5-6］提出一种可调谐加权因子，用于有效区分和分离旋转机械测量信号的闭合和交叉阶分量。Wang等［7］采用多种阶次跟踪技术对变速谐波振动去噪，强调包含裂纹信息的非阶数相关振动，论证了阶次跟踪技术在转子裂纹检测中的优越性。Wu等［8］通过自适应阶次跟踪技术提取阶次特征作为神经网络输入，提出利用网络开发故障诊断系统的人工神经网络技术。张程鹏等［9］通过Compact RIO阶次跟踪和信号包络提取技术相结合的方法，分析风力发电机组齿轮箱变速过程中振动信号非平稳的特点。在滚动轴承［10-15］和齿轮箱［16-20］的故障诊断方面，通过阶次跟踪有效识别和提取到变转速工况下非平稳特征信号，有效识别出非常接近的和微弱的振动特征成分，从而成功地检测出不同类型的齿轮故障。

从以上研究现状看，故障诊断技术只经历了短短几十年的发展，但已经在城市轨道交通列车的轴承、轮对车轴齿轮箱和踏面等的监测诊断方面得到了长足发展和广泛应用。基于列车启停频繁、车速快、车轮高速旋转和受力集中等特点，走行部的部件长期处于摩擦、冲击、振动、腐蚀等自然损耗状态，一旦出现故障，会影响列车的安全性和稳定性，甚至危及乘客生命财产安全。

近年来，走行部在线检测和故障诊断技术快速发展，基于广义共振和共振解调的故障诊断技术在走行部旋转部件故障诊断中得到广泛应用，如岳晓峰等［21］研究团队发表的研究成果。但这些研究成果通常会预设一个二次或多次的列车行为模式，由于列车运行速度随时间变化，运行速度直接取决于车轮的旋转角速度，故其特征频率和故障频率也会随列车的运行速度一同变化，如果采用基于固定时间间隔采样的传统信号采样策略，采集到的故障信号频率不是某一个具体值，而是由列车运行速度决定的范围，同时信号能量会分散在此范围，进而导致故障信号的频率范围模糊且信号强度降低。以列车运行规律固定为前提的阶次跟踪，因为走行部轴承、齿轮及车轮等旋转部件时变工况下振动信号非平稳特点，在实际运用中存在一些不足。

针对此不足，根据城市轨道交通列车启动、加速、减速、停车等频繁启停特点，基于阶次跟踪技术对杭海城际列车走行部的车轮进行振动监测，采集某一时间段内运行数据，通过最小二乘法拟合出车轮角度增量和时间增量之间的关系，引入振动信号，通过传统FFT（Fast Fourier Transformation）和阶次跟踪的方法，得到等时间步长和等角度步长的频谱图，进行对比分析，证明阶次跟踪可有效避免列车行驶过程中由于变速导致的信号采样模糊问题，是一种可靠的列车走行部旋转部件故障诊断技术。

2 基本理论

2.1 阶次跟踪技术

阶次跟踪技术（Computed Order Tracking，COT）是旋转机械非平稳振动信号处理的重要技术之一。对于变转速旋转机械设备（包括牵引电机轴承、齿轮箱轴承等）的故障诊断，相对于参考轴或键相信号进行等角度增量采样时，虽然此信号在时域上是非稳定信号，在角域上却是稳定信号，对角域上的稳定信号进行谱分析便可得到清晰的图谱，即阶比谱。因此，振动信号表示为：

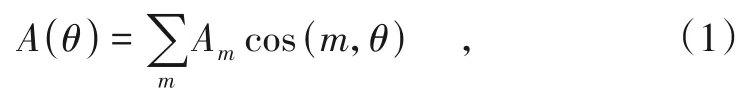
式中：A(θ)为转过角度θ的振动信号幅值；Am为阶次为m的谐波分量幅值（其中，m=1，2，3，…）。

阶次、频率、转速之间的关系为：

式中：f为观测对象的频率，Hz；n为参考轴的转速，r/min。

对于行驶过程中列车的角度增量为：

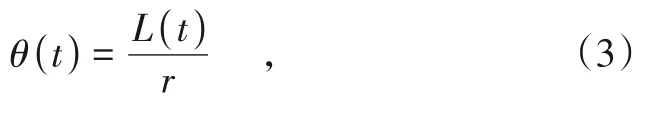
式中：θ(t)为t时刻的角度增量，（°）；L(t)为t时刻列车的行驶位移，m；r为列车车轮的半径，mm。

岳晓峰等［21］研究阶次跟踪在变速箱故障诊断中的应用时，假设变速箱转轴的运动模式为匀加速运动。实际工程中，转轴的运动往往较复杂［22-24］，所以考虑更复杂的匀变加速运动，列车的行驶位移L表示为：

在时域信号中，设键相脉冲的角度增量为Δθ，任意4个相邻时刻(t1，t2，t3，t4)，将其代入式(4)中构成数据矩阵为：

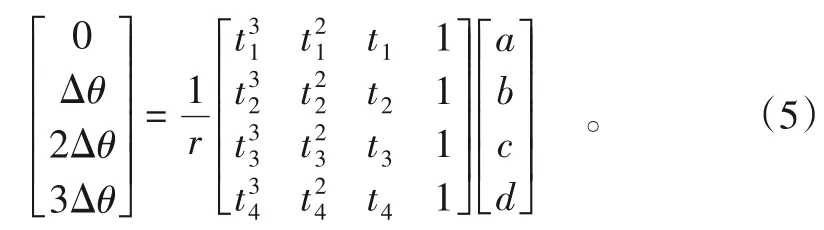
从而求得a，b，c，d的值，回代到式(4)即可求得Δθ和t的关系。

2.2 采样插值和拟合

采样时间间隔决定采样精度，由于实际采集数据过程中，采样结果为离散点，为提高计算精度，更接近实际振动，常采用插值的方式实现离散函数逼近，以满足给定约束。如同采样时间间隔精度一样，插值方法的精度同样决定重采样的幅值精度。

假设在车轮某一部位布置键相标记k，对以上采集的数据进行等角度重采样，采样时，其角度增量Δθk为2π的整数倍，即：

通过最小二乘法拟合出Δθk与tk的关系，在[iΔθ，(i+1)Δθ]之间进行等角度细化，即等角度采样的键相序列θkm，km=1，2，3，…，M，（M为阶次跟踪的信号长度，即单次分析的采样点数）。

以匀变加速度为例，假设原始信号为：

通过最小二乘法对θ与t的关系分别进行二次和三次多项式拟合，并进行阶次跟踪得到的关系见图1。

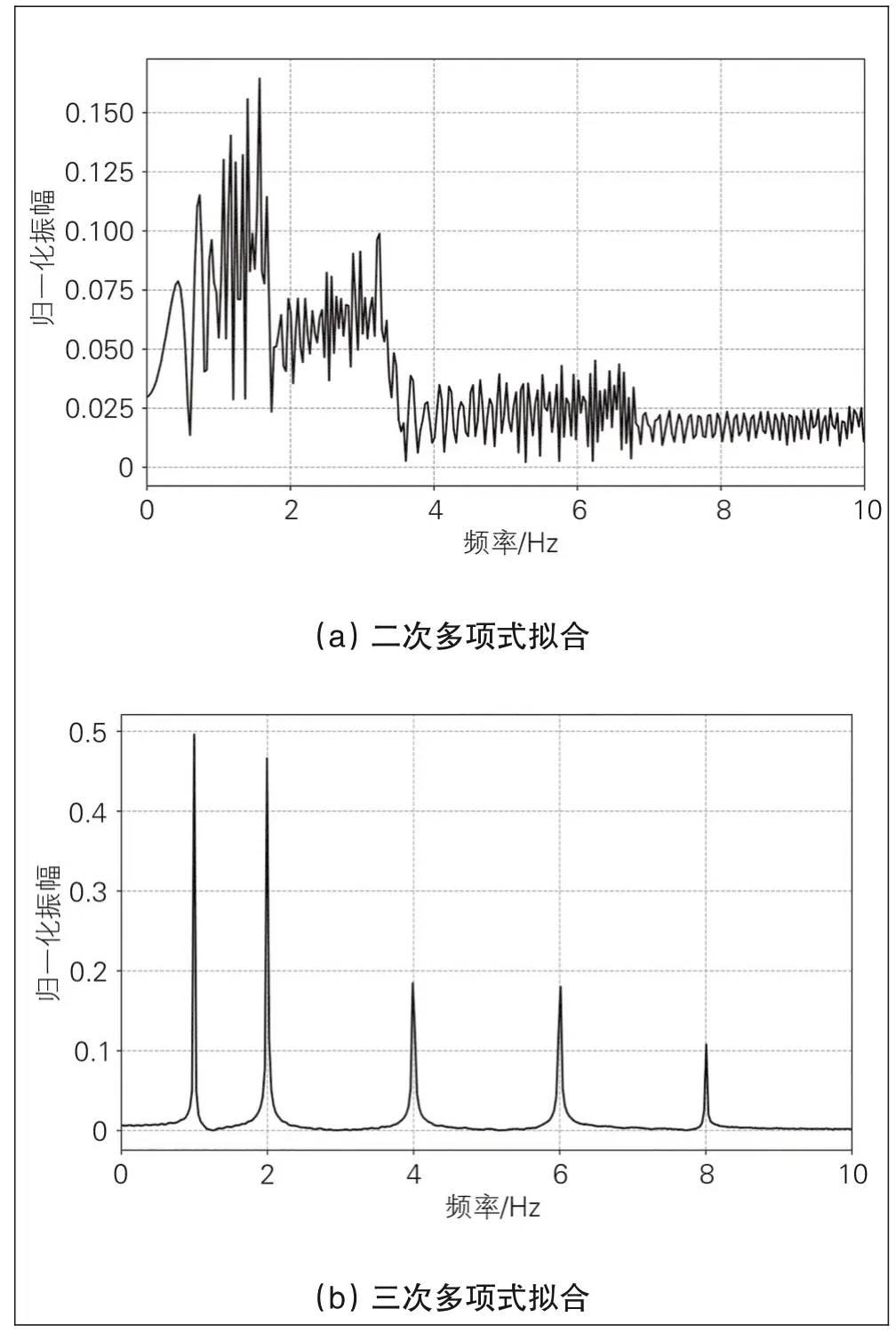
图1 不同拟合关系对阶次跟踪的影响

从以上不同拟合关系得到的阶次跟踪结果可以看出：相比于二次多项式拟合，三次多项式拟合由于和原始信号阶次相同，以该方式拟合后的阶次跟踪更清晰地呈现出振动频率，具有更好的阶次跟踪效果和更高的分析精度。

为提高拟合近似度，可以采用线性插值的方法，对采样的角度间隔进行细化。对式(7)进行线性插值后，分析得到的阶比谱存在一定底噪，这是由于插值方法的阶次跟踪信号无法完美重现原本的信号，导致出现了噪声，该噪声具有的频带宽度远远大于它作用系统的带宽，并且在该带宽中其频谱密度基本可以作为常数考虑，因此，把它当作白噪声处理。

对式(7)中的信号分别进行等时间采样和等角度采样，0～5 s和59～60 s时间段内2种采样方式的对比结果见图2，从图2（a）可以看出，0～5 s时间段内，由于转速较小，等时间步长采样结果优于等角度采样结果，拟合曲线更接近于原始信号；随加速度不断变化，转速随之不断变化，在59～60 s时间段内，等角度采样精度明显优于等时间采样精度。因此，对于变转速运动，采用等角度采样更能得到接近于实际振动的信号［25-26］。

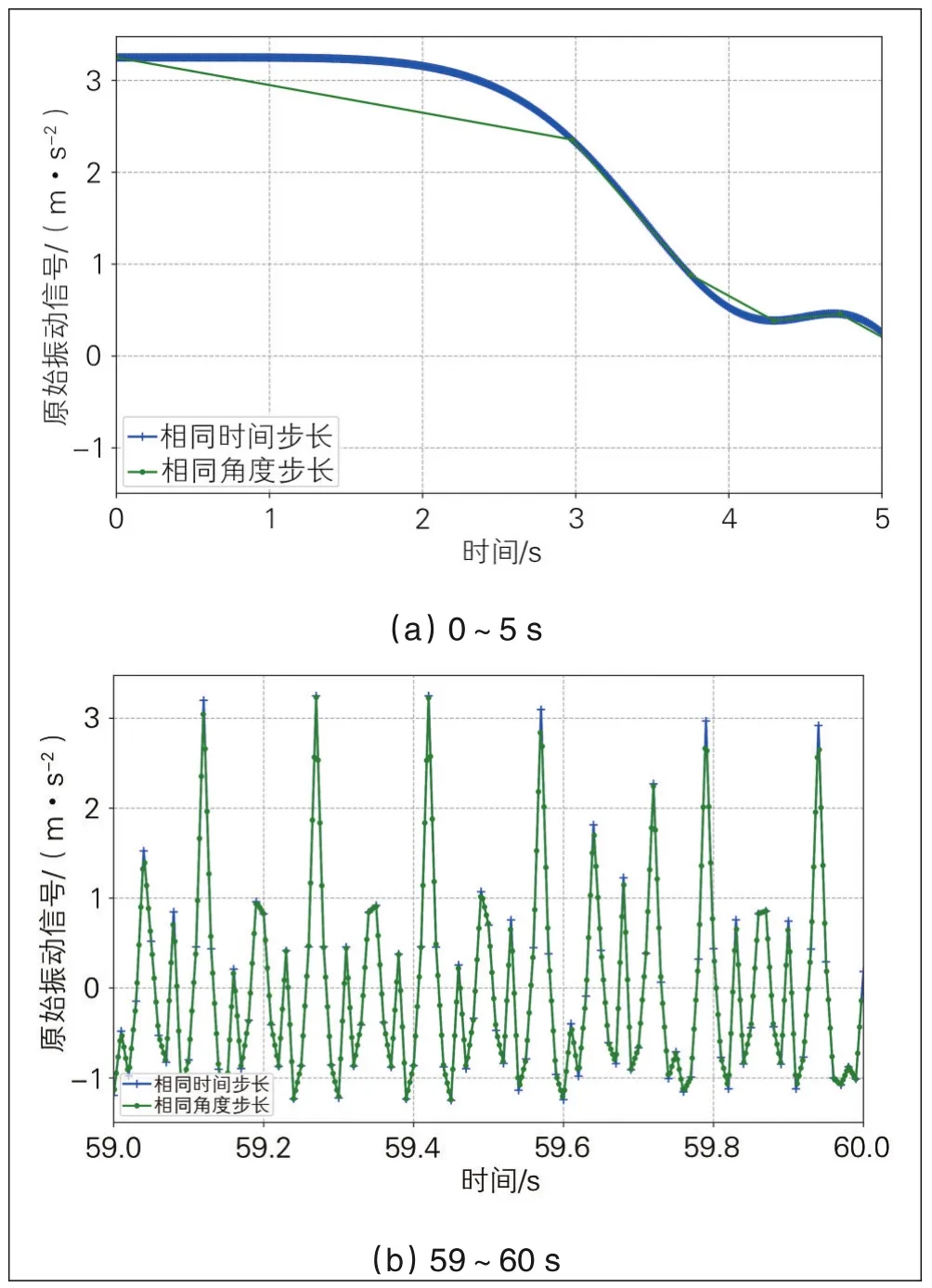
图2 等时间步长和等角度步长采样对比

3 自适应阶次跟踪技术在杭海城际列车的应用

3.1 运行数据实地测量

以齿轮箱这一走行部中最具代表性的旋转部件为研究对象，杭海城际线路采用B型城际列车，其走行部齿轮箱的传动比为117/22，具体参数见表1。实际运行时，对列车运行时转向架各部件的信号均进行分析，以齿轮箱输出轴前轴承的振动幅值信号为研究对象。

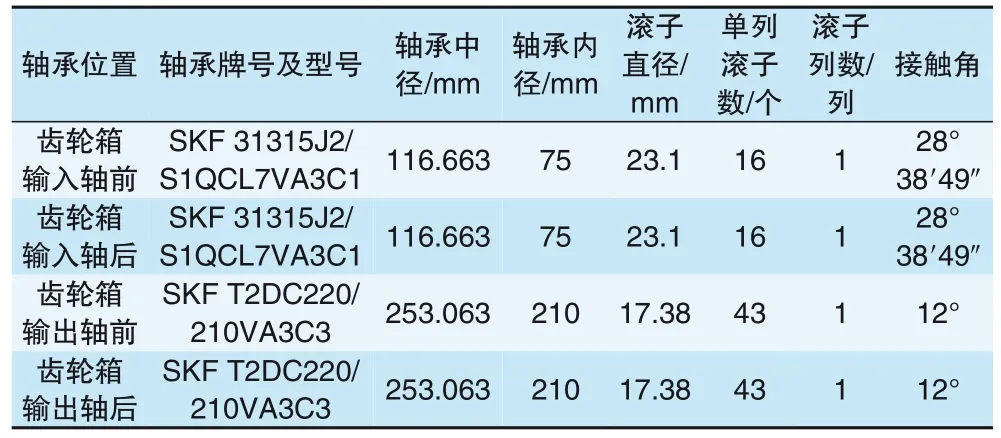
表1 杭海城际列车走行部齿轮箱参数

在列车运行某一时间段内进行等时间采样，采样频率为100Hz。列车行驶过程中加速度与时间的关系见图3。

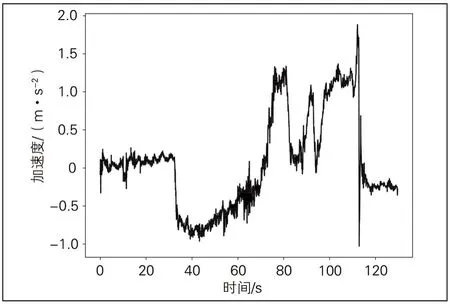
图3 列车行驶过程中加速度与时间的关系

从图3中可以看出，列车在行驶过程中，加速度时刻发生变化，0～30 s时间段内，加速度值近似为0，可以看作匀速运动，35～60 s和60～80 s这2个时间段可以看成加速度增量不同的2段匀变加速运动。为使分析结果更接近实际工况，通过对已有测量数据插值的方式，重新构建等角度间隔的数据集。

引入仿真振动信号模型，模型参数见表2。

表2 仿真振动信号模型参数

3.2 运行模式自适应

图3描述典型的列车匀速稳定运行—刹车—再启动—匀速稳定运行过程，基于图3运动状态、表1提供的振动信号，分别进行时间FFT和阶次跟踪，得到的等时间步长频谱见图4。图4（a）中频率成分繁复杂乱，由于振动信号中的振动频率随时间不断变化，该信号属于非稳定信号，每次执行单一的FFT变换，仅通过改变窗函数大小和形状进行分析，只能处理变化规律恒定的信号，很难适应随时变化的信号，得到谱线反映的是窗内所有频率成分，因此，无法识别故障频率的特征；为更好地接近原始信号，用三次多项式进行拟合，并进行阶次跟踪得到的阶次跟踪频谱见图4（b），从结果看，对等时间采样的信号，采用阶次跟踪得到的阶比谱中频率模糊，依然不能清晰呈现故障特征。

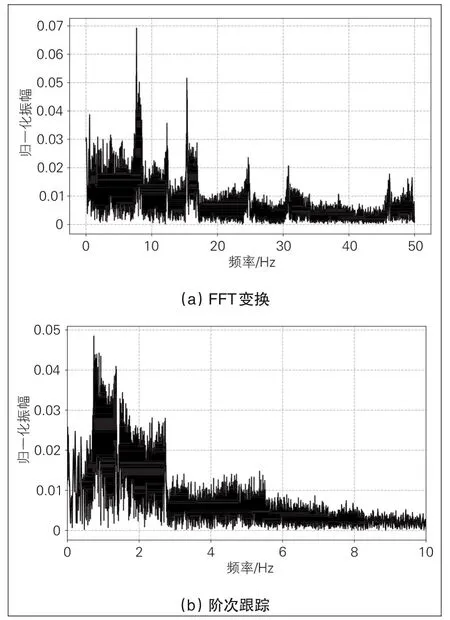
图4 等时间步长频谱

阶次跟踪与FFT变换的区别在于分析域不同，阶次跟踪将FFT变换的等时间采样转换为等角度重采样。对原始振动信号在角度域上重采样，可大幅提高分析频率的精度，以及在后续分析中的准确性。运用最小二乘法拟合出Δθk与tk的关系，在[iΔθ，(i+1)Δθ]之间进行等角度细化，在每个键相之间通过线性插值的方法插入10个值，得到θ与t的近似关系。通过对列车振动信号的拟合和等角度键相插值，得到角度键相和时间序列的关系。随时间变化，角度键相的稀疏程度发生变化，加速度为正时，速度不断增加，等时间间隔内，角度键相分布稠密；反之，分布稀疏。在70 s左右时，列车运行速度最小，车轮的转动角速度也最小，等时间间隔内，角度键相最稀疏。

通过等角度重采样和等角度键相间线性插值，得到重采样信号并进行阶次跟踪，得到的阶次频谱见图5，图中可以清晰地看到阶次分别为1、2、4、6、8的谐波成分，与仿真的振动信号频率成分吻合。对于变转速运行的复杂工况，阶次跟踪可有效避免等时间采样导致的采样模糊、故障频率的频率范围模糊且信号强度低等问题。

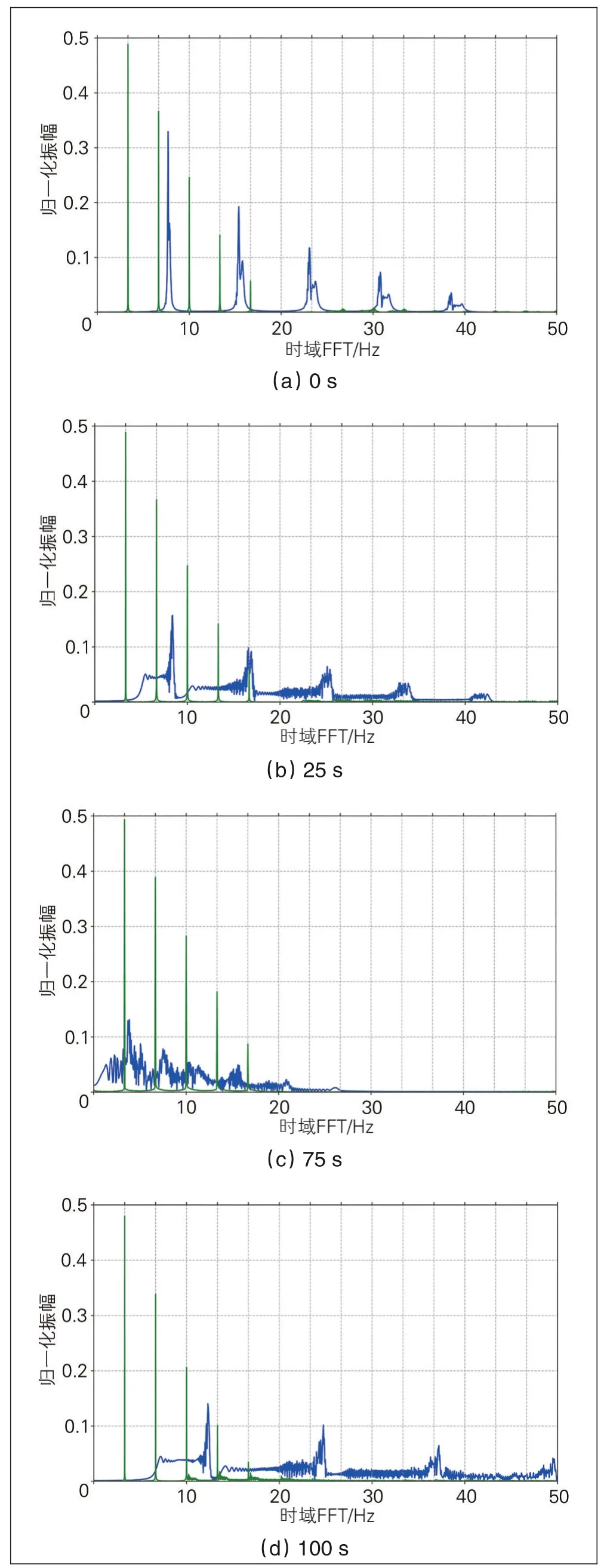
图5 阶次频谱

3.3 运用小结

在杭海城际列车的走行部在线监测系统中，同时采集时域信号和阶次跟踪信号，用于对比不同故障在列车不同运行状态下的不同表征。在对比过程中，可以清晰地看到对于典型的列车启停过程，基于多项式拟合的阶次跟踪难以准确得知故障频率，使用提出的自适应阶次跟踪技术，可以更准确地捕捉到故障信息。

4 结束语

城市轨道交通列车启停频繁、车速变化繁杂，但车轮的行驶速度始终取决于车轮的旋转角速度。在高速旋转且受力集中的情况下，基于等时间采样的振动信号，信号能量分布于与列车行驶速度相关的范围内，即故障频率将分散于某一频域范围，不能准确得知故障频率和故障原因。

采用自适应阶次跟踪技术时，通过等角度采样的方式，自适应调整采样频率，将时域上的非稳定信号转化为角域上的稳定信号，通过阶次跟踪得到阶比谱，可以清晰地看出阶次谐波成分，精确地识别故障频率。

常见的阶次跟踪技术需要预先假设一个二次或者多次的关系对设备运行规律进行拟合，一旦设备的运行规律较复杂，则难以准确进行阶次跟踪。使用自适应阶次跟踪技术可以适应设备各种复杂的运行模式，在城市轨道交通列车走行部旋转部件实际监测运用中可以更好地捕捉到设备和故障特征，使阶次跟踪技术在城市轨道交通列车故障诊断中具有更广阔的应用前景。