仿尺蠖多模式爬壁机器人设计与控制方法研究

眭 翔，徐林森，周瑞吉，刘进福，龙 杰

(1.常州信息职业技术学院 常州市高端制造装备智能化技术重点实验室，江苏 常州 213164；2.中国科学院 合肥物质科学研究院，合肥 230032；3.中国科学技术大学，合肥 230026；4.河海大学 机电工程学院，江苏 常州 213022；5.常州工业职业技术学院 智能控制学院，江苏 常州 213164)

0 引言

目前对于高层建筑清洁与检测、大型化工罐体焊接与检测、管道和隧道等狭小空间安全巡检等场合，传统条件下一般由人工作业来完成，有时在一些恶劣、狭小环境人工操作也很困难，不仅效率低下，而且经常发生安全事故，每年因为检测不到位或意外事故产生了大量的损失，因此爬壁机器人成为机器人研究领域的热门课题，众多国内外学者对爬壁机器人进行了相关研究。在文献[1]中，国内哈尔滨工业大学学者研究了多种结构的爬壁机器人，但是主要是以导磁性材料为核心，只能适应导磁性壁面。文献[2]中广东工业大学学者研发了一种双足爬壁机器人W-Climb，属于足式机器人，运动能力较为灵活，但是爬行方式单一，只能吸盘吸附行走。国外学者研究更早，文献[3]中斯坦福大学研究者采用金属钩刺设计了一种可以依附于墙面的仿生装置，质量很轻，负载能力偏弱。文献[4]中以色列学者结合足式机器人及螳螂足底附着机理，设计了四足式仿生机器人，仅依靠贴合悬挂的方式附着与墙面。上述研究表明，目前国内外爬壁机器人的研究虽然已经有些成果，但是仍处于功能单一、结构简单的状态，缺乏一定的可靠性，存在较大的优化空间。

尺蠖结构简单、体型小巧、运动迅速，本研究基于自然界尺蠖类生物的壁面攀爬机理[5-7]，结合仿生技术，研发了一种仿尺蠖多模式爬壁机器人，该机器人属于一种仿生多连杆关节机器人，其关节采用具有扭矩控制功能的伺服电机。结合实际应用场景，构建了运动学模型，对机器人采用进行基于关节扭矩的力控方式，探索了基于极坐标理论的机器人步态控制方法，并在实际样机平台进行了测试，验证了爬壁机器人的运动学模型的正确性和步态控制方法的平稳性。

1 仿尺蠖多模式爬壁机器人设计

尺蠖是一种节肢类生物，在附着时它可以利用头部和尾部的微小倒刺结构实现对物体表面的抓附，在运动时身体通过不断的伸展和收缩来实现前进和后退，结合尺蠖的运动规律[8]，简化其运动模式，本研究设计了多模式的仿尺蠖爬壁机器人。

仿尺蠖爬壁机器人虚拟样机如图1所示，尺蠖机器人是一种多连杆的双足机器人，为了增加其负载能力，没有选择一些学者经常采用的软体材料或者记忆合金材料[9-10]，而采用在两个足部之间由一个三自由度机械臂连接的方案。每条大臂长10 cm，总长75 cm，采用铝合金制作，在机械臂上安装了3个配有高精度绝对编码器的伺服电机，每个电机扭矩20 N·m，通过CAN协议实现精确的位置和扭矩控制。

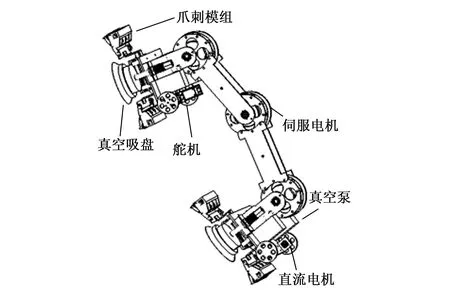
图1 仿尺蠖多模式爬壁机器人虚拟样机

仿尺蠖爬壁机器人可以实现多模式运动，其中攀爬模式是重要功能，为了实现附着功能，爬壁机器人足部设计了两种附着机构[11-12]，分别是真空负压吸附和仿生爪刺抓附两个功能模块。真空负压吸附模块在每个足部安装了两个真空吸盘，通过真空泵抽真空来提供附着力。仿生爪刺附着装置由两对爪刺模组构成，如图2所示，爪刺模组安装在足底部，每只足包含一对爪刺模块，每一个模块由多个爪刺足片组成，每对爪刺模块的抓附由通过安装在底部的高扭矩舵机控制，舵机可以针对不同的壁面控制张合的大小，以此实现抓附力度的控制。通过这两个吸附装置的配合，可以实现在平整表面和粗糙壁面等多种环境下的有效吸附。

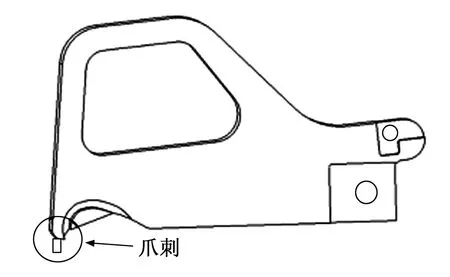
图2 爪刺足片

爬壁机器人除了可以利用两种附着装置实现多种壁面的攀爬，同时为了解决水平面到垂直壁面过渡的问题，机器人安装了四个直流电机，可以在地面上行走，提高了机器人多种类型壁面的适应性，实现了多模式的运动功能。

2 仿尺蠖多模式爬壁机器人运动学建模

2.1 多模式爬壁机器人坐标系

当机器人做爬壁运动时，通过两足的不断交替吸附以实现循环攀附，同时身体关节不断伸展和收缩以实现上下运动[13]。对于这两种运动，建立如图3所示的坐标系，图中以攀爬时伸展姿态建立坐标系。机器人的一只足命名为OA，与墙面保持固定的OA为基座标，此处简化模型，选择以机器人三个关节分别命名为OA0,OA1,OA2，四个连杆的长度分别为L0,L1,L2,L3。定义连杆L0为机器人的基座标系{0}，关节OA0为坐标系{1}，关节OA1为坐标系{2}，关节OA2为坐标系{3}。

图3 多模式爬壁机器人坐标系

2.2 多模式爬壁机器人运动学正解

本研究采用D-H参数法建立机器人运动学模型[14-15]，如表1所示，定义各个关节轴心线为i，表中αi-1为轴心线i-1与轴心线i的夹角，αi-1为轴心线i-1与轴心线i的距离，即为连杆的长度，θi是指各个关节的角度,di则表示为轴心线i-1与轴心线i的垂直距离，对于相互平行的轴心线来说，该值一般为0。

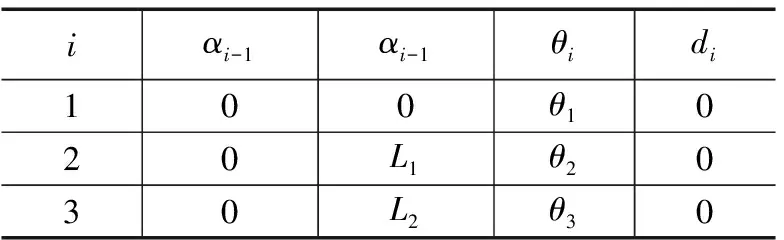
表1 仿尺蠖多模式爬壁机器人D-H参数表

将坐标系{i}经过变换使其与{i-1}重合，则坐标系{i}到坐标系{i-1}的变换矩阵为：

即：

(1)

式中，c1表示的是cos(θi)，si则表示sin(θi)，以及下文出现的cij和sij分别为cos(θi+θj)和sin(θi+θj)。

当i分别为1、2、3时，得到连杆i相对于基坐标的变换阵如下：

(4)

将以上矩阵依次相乘，得到机器人末端位姿在笛卡尔坐标系中的矩阵：

(5)

将式(2)～(4)代入式(5)中获得末端关节坐标系OA2在基坐标系OA0中的位姿描述矩阵：

(6)

式中，cijk和sijk分别表示cos(θi+θj+θk)和sin(θi+θj+θk)，(px,py,pz)为机器人末端关节坐标系在笛卡尔空间下的坐标位置，Ø爬壁机器人末端执行器的姿态。

2.3 多模式爬壁机器人运动学逆解

在仿尺蠖爬壁机器人实际应用中，经常需要运动到目标位置，即需要将已知的笛卡尔空间坐标转换成关节空间位置，该机器人的运动学逆解方法如下[16-17]，首先建立运动学方程组：

(7)

对式(7)中的式(1)和(2)左右平方和相加得：

(8)

以此分别求得：

(9)

(10)

由双变量正反切公式计算得到：

θ2=Atan2(sin(θ2),cos(θ2))

(11)

由机械结构限制和约束条件得到唯一解：

(12)

结合式(7)和(12)可以解算出θ1的值。为此改写式(7)为：

(13)

式中,

(14)

假设：

(15)

γ=Atan2(k2,k1)

(16)

则有：

(17)

代入式(13)得：

(18)

因此可以得到：

(19)

故：

(20)

θ1=Atan2(py,px)-Atan2(k2,k1)

(21)

Ø=θ1+θ2+θ3=Atan2(sØ,cØ)

(22)

θ3=Ø-θ1-θ2

(23)

综上可得运动学逆解方程如下：

(24)

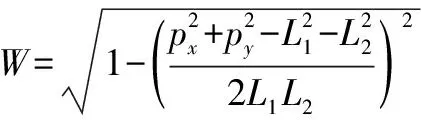
获得爬壁机器人运动学逆解后，可以根据笛卡尔坐标系空间位置解算爬壁机器人各关节角度信息，通过控制器及编码器数值可以进行角度闭环控制，从而实现爬壁机器人的灵活运动。

3 仿尺蠖多模式爬壁机器人步态控制

仿尺蠖多模式爬壁机器人可以实现地面—壁面过渡、壁面攀爬、壁面—天花板过渡三种状态的运动[18]，其中壁面攀爬为重要功能，本文重点分析。尺蠖通过不断循环完成躯体的伸展姿态和收缩姿态，实现上下运动，同时双足配合在墙壁上交替抓附来完成自身的吸附脱附等动作。参考自然界尺蠖生物的攀爬原理和运动机理来设计一种高效稳定的步态控制方案，本文将这种步态称为尺蠖步态，需要控制3个关节实现爬壁机器人的尺蠖步态控制。仿尺蠖爬壁机器人攀爬状态如图4所示，机器人在攀爬过程中有伸展、收缩、驻留3种姿态。

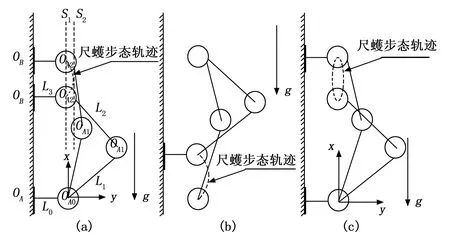
图4 仿尺蠖多模式爬壁机器人攀爬运动模式

当机器人双足吸附在墙面时，即为驻留状态，两只脚都依靠真空吸盘吸附，当准备向上攀爬时，机器人首先脱附上足OB，机器人通过三个伺服电机协同工作，使机器人运动到伸展状态，并且保持足底与墙面保持平行且留有安全距离，避免发生碰撞。如图4(a)所示，当机器人从初始状态向上达到伸展状态时，机器人的关节OA2的具体运动路径如图中的虚线所示，且过程中避免角度过大，导致机器人发生后仰倾覆，即虚线S1和S2间距最小。当完成伸展动作后，爬壁机器人下足需要进行收缩运动，如图4(b)所示，其下足进行向上运动，虚线为机器人下足的关节运动轨迹，完成后双足吸附在墙面，进行驻留，机器人不停实现伸展—收缩—驻留循环动作就可以实现攀爬运动。

从图4(c)中可以看出上足关节OA2的运动轨迹如图中虚线，为一个类似右边半个椭圆的轨迹。基于这个半椭圆，补足另外半个椭圆，并以此轨迹进行建模[19]。本文采用基于极坐标理论的尺蠖步态轨迹规划方法，首先时间信号t为基础，建立两个极坐标方程，分别对应笛卡尔空间下的X轴和Y轴的轨迹信息。具体的数学模型如式(25)所示：

(25)

式中，X和Y分别代表机器人末端连杆坐标系在笛卡尔空间下的坐标位置，即为(X,Y)。Xα和Yα为机器人末端连杆坐标系的初始位置相对于基座标系的初始位置偏移量，XR与YR则为尺蠖步态轨迹在笛卡尔坐标系下在X轴与Y轴上的振幅，调节XR可以改变调整机器人的运动步长，调节YR能够调整机器人与墙面的最远距离，但是该参数的设置不宜过大，否则机器人会出现后仰倾覆的问题。t为实时时间信号，T是一个正增益系数，该系数可以直接影响到机器人的运行速度。

为了对模型进行分析，实验设置了三组参数来进行相互对比验证，各个参数设置如式所示：

(26)

在上述仿真平台中进行实验仿真，得到如图5所示的三组数据，三个图分别表示以上三组数据下机器人末端连杆坐标系在笛卡尔空间下的运动轨迹，从图(a)、(c)、(e)中可以看出伴随着Xα和Yα的逐渐增大，其椭圆形轨迹的X轴和Y轴的亦随之增大。其中X轴的数据变化范围分别是(1,3),(1,5),(2,8),Y轴的数据变化范围分别是(1.5,2.5),(2,4),(3.5,6.5)，并且X轴的数据跨度为XR的2倍，Y轴的数据跨度为YR的2倍。故机器人的运动步长和运动幅度可以由Xα和Yα的值进行调整。

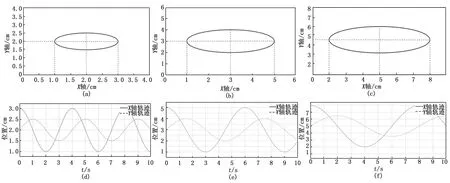
图5 步态轨迹规划仿真实验数据图

从图5(b)、(d)、(f)中的曲线可以得到，随着增益系数T的不断增大，曲线在单位时间内的振动频率明显逐渐减小，即在相同的时间内，T值越大，末端连杆坐标系在笛卡尔空间坐标系下完成的椭圆轨迹数量就会相应减少，也就是T值越小机器人运行速度越快，T值越大运行速度越慢。由此实验验证可知，该基于极坐标的仿尺蠖爬壁机器人的步态控制方法是有效的。

4 仿尺蠖多模式爬壁机器人控制系统设计与实验

4.1 多模式爬壁机器人控制系统硬件设计

完成仿尺蠖爬壁机器人的运动学建模、步态规划仿真后，基于这些数据，对于仿尺蠖多模式爬壁机器人的控制系统，设计了上、下位机两个部分。上位机部分采用基于Android平台的手持式终端设计，下位机部分采用基于STM32F407嵌入式控制器的主控系统。

上位机手持终端的设计如图6所示，终端采用无线图数传输模块接收下位机传输的视频信息和控制信息，底层控制芯片采用STM32F103控制器采集摇杆和按钮的信号，同时接收下位机上传的电机、传感器等反馈信号，最后将采集的控制数据打包传输给Android平台。上位机主监控平台采用Android平台，屏幕上设计监控区和设置区，其中监控区显示爬壁机器人的现场视觉监控画面及监控的电压、电流、压力、速度和角度等参数，设置区提供信道选择、工作模式、电机参数等设置，后台处理程序同时把这些控制数据下发给机器人。

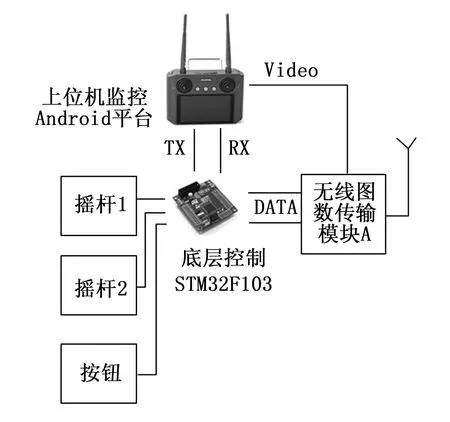
图6 上位机手持终端

爬壁机器人控制系统结构如图7所示，主控采用STM32F407控制器，外接伺服电机、舵机、真空泵控制模组、直流电机和无线图数传输模块。主控器首先接收上位机手持终端通过无线图数传输模块下发的配置参数，写入存储器后，启动主程序。其中主控通过CAN总线控制3个关节，关节为驱控一体结构，同时带扭矩控制的伺服电机，可以提供24 N·m的扭矩。

图7 下位机控制系统

吸附装置采用真空泵和电磁气阀组合控制实现吸附和脱附功能[20-22]，当需要吸附时真空泵打开进行吸附，控制器可以通过压力传感器检测吸附效果，当需要脱附时，控制器一边控制真空泵继电器失电停止抽真空，同时为了加快脱附，另一边通过控制加装的电磁气阀得电加快放气。爪刺模组的控制，通过两个舵机来控制两个足端的爪刺的张合，在两足吸附后，通过控制爪刺的收缩量来控制抓附的力度，从而增强吸附能力，提高了多种粗糙度壁面的适应能力。机器人同时可以在平面到壁面的过渡进行行走，其通过主控驱动直流电机以实现，这个行走功能增加了机器人的运动模式，适应仿尺蠖多模式爬壁机器人的各种运动场景。

4.2 多模式爬壁机器人控制系统软件设计

完成控制系统硬件设计后，需要进行机器人控制软件设计[23-25]，仿尺蠖多模式爬壁机器人软件控制程序流程如图8所示，左侧为下位机主控程序结构，右侧为上位机监控端程序结构。首先上位机监控端主要是视频显示和收发控制数据，与下位机通过通信关键帧来判断连通状态，及时发现通信故障并显示故障代码。下位机主控通过上位机下发通信状态关键帧来判断通信链路状态，系统启动后首先进行姿态复位操作，初始化机器人初始位置，记录编码器初始值。反馈复位状态，等待监控终端指令，当接收到终端指令后，根据控制参数，启动对应的运动模式。不同的运动模式对应不同的步态轨迹算法，算法相应的控制机器人各个关节运动姿态，主控制器实时将关节伺服电机的如电压、电流、位置、角度和扭矩等信息上传到算法模块进行实时动态调整，同时主控也监测关节数据以及控制系统电压、电流、真空压力等信息，如果发现异常及时报警。

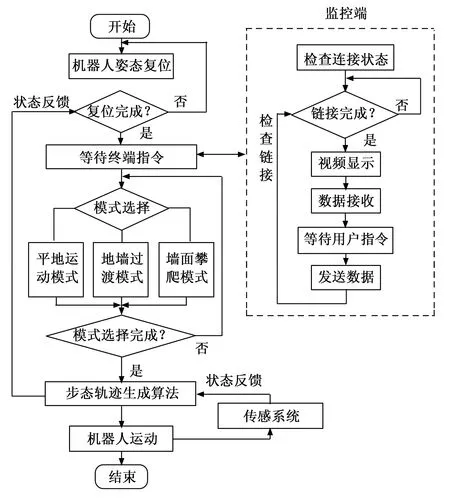
图8 控制系统软件程序流程图

4.3 多模式爬壁机器人攀爬实验

根据以上仿尺蠖多模式爬壁机器人控制系统搭建，结合步态规划仿真数据，进行了机器人攀爬实验。仿尺蠖多模式爬壁机器人自重约9 kg，总长约75 cm，仿尺蠖爬壁机器人攀爬实验如图9所示。

图9 攀爬实验

首先机器人根据箭头方向以直线姿态前进到目标墙壁，通过前足的吸附及爪刺收缩实现固定，之后开始地墙过渡动作，上位机发出过渡指令后，下位机主控根据指令运行过渡程序，控制3个关节实现翻转，机器人从直线状态转换到爬壁状态，之后后足进行吸附固定，整个过程耗时1.5 s。之后机器人双足吸附在壁面，进行向上攀爬，经过测试，机器人设置路程1 000 mm，负载2 kg时，速度可达90 mm/s，实验验证了多模式爬壁机器人攀爬功能的可靠性，但是由于机器人吸附和脱附比较耗时间，所以机器人整体目前速度不是太快，后期可以进一步优化步态算法。

同时采集的关节3的轨迹角度误差数据如图10所示，在负载测试情况下，关节3轨迹误差在短暂振荡超调后，于0.24 s左右进入稳定状态，实验证明机器人在运动过程中具有良好的稳定性，实现了各项预设目标。

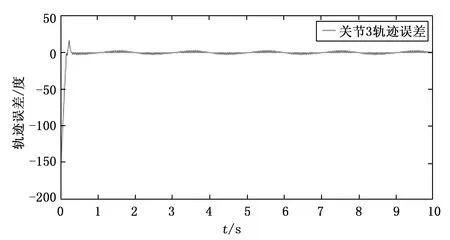
图10 关节轨迹误差图

5 结束语

本文结合自然界尺蠖类生物的壁面攀爬机理，利用仿生爬壁技术，研发了一种仿尺蠖多模式爬壁机器人，机器人设计了真空吸附和爪刺抓附两种吸附装置，并建立了机器人运动学模型，进行了正、逆运动学求解。同时研究了基于极坐标理论的机器人步态控制方法，并通过地墙过渡和壁面攀爬测试，实验表明该设计可以完成爬壁机器人的地墙状态切换，并且壁面攀爬速度可达90 mm/s，运行过程稳定，具有良好的抗倾覆能力。本文研究的仿尺蠖多模式爬壁机器人建模与控制方法为双足类仿生机器人进一步研究提供了参考。