基于深度学习的卫星遥感图像边缘检测方法

叶应辉

(吉林大学 地球探测科学与技术学院，长春 130026)

0 引言

遥感图像指的是用于记录地物电磁波信息的照片或胶片，包括航空像片、卫星相片两种组成形式。通常情况下，经过计算机软件处理后的遥感图像被称为数字图像，大多数以摄影或拍摄的方式获取，在经过图像扫描仪的转换处理后，其表现形式可由噪点信息转化成为完整的地物景观图像[1]。在实施卫星遥感图像边缘检测的过程中，由于节点处信噪比指标的数值水平并不能达到实际需求标准，一部分模糊噪点会与图像原始节点混合在一起，这就对遥感图像的清晰程度造成了严重影响[2]。

近年来，如何去除噪点、增强遥感图像的清晰度是众多学者的研究目标，且其已经获得一定成果。如文献[3]针对遥感图像去噪后易模糊的问题，提出基于方向和结构特征的遥感图像条带噪声分离方法。该方法虽然能够确定卫星遥感图像边缘节点之间的关联度水平，但却并不能将模糊噪点与图像原始节点分离开，故而并不能使卫星遥感图像的清晰度保持较高数值水平。文献[4]提出的基于FD-RCF的高分辨率遥感影像耕地边缘检测方法。该方法充分利用了空洞卷积结构，构建了可应用于卫星遥感图像的边缘检测模型，再利用该模型完成遥感图像的边缘检测。经实验表明，其虽可提高检测画面的清晰度，但对于边缘检测精度的提高仍然不足。文献[5]针对高分辨率遥感影像边缘检测易模糊的问题，提出了基于MSR-cut的高空间分辨率遥感影像边缘检测分割方法。该方法先利用分水岭分割算法对影像进行过分割，形成多个超像素区间，然后构建评价函数得出其最优分割尺度，对像素区域进行初步合并，得到其粗分割结果，最后结合各地物的边界权重信息进行影像的精细分割。该方法虽然可提高边缘检测的分割精度，但其鲁棒性不强，无法大范围应用。

深度学习算法可对图像数据信息的二维结构进行重新定义，还可联合定义权值与特征指标权值，确定相邻学习节点之间的相似性程度。相比于其他算法不但可大大减少数据运算量，还可从根本上解决数据信息样本分布不均衡的问题。基于此，本文以深度学习算法为基础，设计一种新型的卫星遥感图像边缘检测方法。

1 基于深度学习的卫星遥感图像识别

卫星遥感图像的识别以Softmax分类器设计为基础，再联合深度学习算法，建立完整的图像节点数据集合，最后卷积、池化处理原则，得到准确的图像边缘节点识别结果。

1.1 Softmax分类器

Softmax分类器是实现深度学习算法的执行基础，在数据集合空间中，能够描述出信息参量节点的排列与分布形式，且要求所有学习信息参量的取值都要满足回归性查询原则[6]。

假设对于待学习卫星遥感图像边缘节点训练集{(e1,w1),(e2,w2),…,(eα,wα)}来说，e∈[1,α]、w∈[1,α]的取值条件同时成立，且指标e、指标w不会等于同一物理自然数。针对深度学习算法原理，可将假设分类函数q(e,w)表示为：

(1)

式中，β表示与指标e相关的分类系数项，δ表示与指标w相关的分类系数项。

规定χ1、χ2、…、χα表示α个不同的卫星遥感图像边缘节点学习系数，且χ1≠0、χα≠1的不等式条件同时成立。联立上述物理量，可将基于深度学习算法的卫星遥感图像边缘检测节点Softmax分类器构建表达式定义为：

(2)

其中:ε表示待学习数据项的初始分类赋值指标，t1、t2表示两个随机选取的待学习数据定标值，且t1≠t2的不等式条件恒成立，γα表示数据信息参量学习深度指标的最大取值结果。为使卫星遥感图像边缘检测节点得到准确的分类与处理，在建立Softmax分类器表达式时，应避免对相关参量指标进行重复取值，且关联系数之间的物理差值水平也不宜过大。

1.2 图像节点数据集

对于卫星遥感图像的边缘检测区域而言，图像节点数据集的建立充分体现了Softmax分类器闭环的实际应用能力。在深度学习算法的作用下，图像节点数据集合意在将待检测边缘节点汇聚起来，并根据既定原则，对这些节点参量进行重新排序，直至检测主机能够将整幅卫星遥感图像完全收录在内[7]。为使图像节点数据集合满足深度学习算法的构建需求，首先应确定隐含层节点所处位置，根据相邻边缘节点之间的权重配比关系，建立完整的图像标签结构；然后要按照初始节点与终止节点间隔距离，建立与卫星遥感图像相关的检测点分布表达式；最后以Softmax分类器定义表达式为标准，判定当前数据集合是否满足边缘检测方法的实际应用需求[8]。完整的卫星遥感图像节点数据训练流程如图1所示。

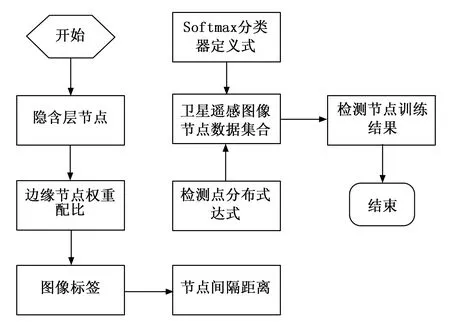
图1 卫星遥感图像节点数据的训练流程

设δ表示卫星遥感图像的边缘区域定义系数，t表示检测指令执行时长，o1、o2表示两个随机选取的图像节点定义项指标，且o1≠o2的不等式条件恒成立，r表示图像节点数据集合中的算子定义项。在上述物理量的支持下，联立公式(2)，可将基于深度学习算法的卫星遥感图像节点数据集合表示为：

={r|r=δy+(t×)}

(3)

为避免卫星遥感图像边缘检测结果出现偏差，在建立图像节点数据集合之前，需对所涉及数据信息参量进行集中训练处理。

1.3 卷积和池化处理

由于卫星遥感图像具有明显特性，所以在实施检测算法的过程中，要求节点数据集合中参量指标的统计特性必须保持一致，简单来说，就是待检测边缘节点之间不能存在冲突。因此，图像上所有节点的学习特征都完全相同。卷积处理则是在一致性原则基础上制定的卫星遥感图像节点处理法则[9]。设ε、γ表示两个不相关的遥感图像节卷积处理系数，iε表示基于系数ε的节点定义权值，iγ表示基于系数γ的节点定义权值，且iε指标、iγ指标的取值同时属于图像节点数据集合。联立上述物理量，可将卫星遥感图像边缘检测节点的卷积化执行原则表示为：

(4)

池化处理原则可根据深度学习算法确定卫星遥感图像边缘检测节点的表现特征[10]。若备选节点取值完全属于图像节点数据集合，则可将卫星遥感图像边缘检测节点的池化执行原则表示为：

(5)

式中，κ、ι表示两个不相等的遥感图像节点池化处理系数，pκ表示基于系数κ的图像节点池化特征，pι表示基于系数ι的图像节点池化特征，φ表示待检测向量的池化处理定义项指标，且pκ指标、pι指标的取值也同时属于图像节点数据集合。出于综合性考虑，深度学习算法的构建必须参考卫星遥感图像边缘检测节点的卷积与池化处理表达式。

2 卫星遥感图像拼接处理

本文引用SURF算法完成卫星遥感图像的拼接处理，先建立积分图像，然后经过尺度空间建立、图像边缘特征点配准及梯度信息熵计算的处理流程实现待检测卫星遥感图像的拼接与处理。

先建立积分图像，所谓积分图像就是对原始图像原点到该点进行积分所得到的图像。设P(x,y)为原始图像原点O到点P的像素和，I(i,j)表示原始图像对应像素点(i,j)的值，则积分图像中点P的值可表示为:

(6)

2.1 尺度空间

所谓尺度空间就是一幅图像通过一定算法那获得空间一些列分辨率不同的图像。通常情况下，一幅未知卫星遥感图像中会包含大量的边缘节点特征内容，若不能准确预测出图像特征节点所在的尺度空间，则会使边缘区域内检测节点所包含的特征参量被忽视，从而使得最终所得检测结果并不能完全满足实际应用需求[11]。故而对于卫星遥感图像来说，为使其边缘性检测结果能够反映出整幅图像内节点特征的分布形式，应根据其算法构建完整的尺度空间。本文利用SURF算法，采用不同大小的滤波器对图像进行处理，从而得到空间图像金字塔。采用该种方法可使得图像的多尺度空间表现出平面图像的空间特征，保证图像拼接的旋转不变性，其所采用的箱式滤波器效果近似于高斯二阶偏导数，其效果如图2所示。

图2 箱式滤波器近似效果

采用该种方式提高传统尺度空间建立计算的复杂性，缩短计算时间，保证计算数据的性能[12]。接下来，设k1表示边缘区域内的图像节点特征参量，k2表示其他区域内的图像节点特征参量，且k1≠k2的不等式条件恒成立，Δφ表示单位时间内图像特征节点检测数量，利用上述参数对尺度空间表达式进行定义：

(7)

2.2 特征点提取及配准

(8)

为减少数值运算量，默认卫星遥感图像边缘区域内的待检测特征点不会出现-覆盖性排列的表现形式。

2.3 梯度信息熵

为增大卫星遥感图像的基础分辨率水平，使待检测特征参量在边缘区域内呈现较为清晰的分布排列状态，在完成图像拼接处理后，还需根据特征参量的实时分布形式，计算梯度信息熵指标的具体数值[15]。所谓梯度信息熵是指待检测卫星遥感图像所反映出的节点分辨率情况，一般来说，其数值结果越大，就表示边缘区域内待检测节点与其他区域内普通节点之间的差异性越大，获得实时检测结果所需的等待时间也就越短。故而在实施卫星遥感图像边缘检测指令时，应尽可能使梯度信息熵指标达到其极大值[16]。设ν为卫星遥感图像梯度熵增系数的初始取值，在深度学习算法作用下，该项物理指标的最小值只能等于自然数“1”，f为卫星遥感图像边缘区域内的特征点梯度值度量系数，d为深度学习算法作用强度，ϖ、θ表示两个随机选取的信息熵增量标度值，且ϖ≠θ的不等式条件恒成立。联立上述物理量，可将卫星遥感图像边缘检测区域内的梯度信息熵指标计算表达式定义为：

(9)

出于计算简便性考虑，在执行卫星遥感图像边缘检测算法时，ϖ系数、θ系数的初始取值都等于物理自然数“1”。

3 卫星遥感图像的边缘检测

本次研究基于深度学习中的CV算法对卫星遥感图像进行边缘检测，其需同时求解一阶微分边缘算子、二阶微分边缘算子，然后根据合适的微分算子计算图像的梯度幅值与双阈值，以此完成其边缘检测。

3.1 一阶微分边缘算子

(10)

(11)

3.2 二阶微分边缘算子

二阶微分边缘算子也叫过零点算子。对于卫星遥感图像来说，在边缘区域处，如果二阶微分函数同时存在两个或两个以上的零值，才表示在该取值条件下的边缘算子系数能够满足深度学习算法的处理需求[19-20]。规定卫星遥感图像边缘检测算法的二阶微分函数为：

F=ζ(v1+v2+…+vn)2

(12)

其中：ζ表示基于深度学习算法的二阶微分偏导系数，且系数ζ的最小取值结果也始终大于物理自然数“1”，v1、v2、…、vn表示定义编号由1-n的微分节点标记系数，n表示最大微分向量。

在公式(11)的基础上，设bmin表示二阶微分算量的最小取值结果，bmax表示二阶微分算量的最大取值结果，m表示卫星遥感图像边缘检测算量定标准，ω表示基于深度学习算法的二阶运算系数，τ表示二阶微分偏导向量。联立上述物理量，可将基于深度学习算法的二阶微分边缘算子计算表达式定义为：

(13)

在对卫星遥感图像边缘节点进行检测的过程中，一阶微分边缘算子、二阶微分边缘算子不可能同时取得零值结果。

3.3 梯度幅值

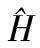
(14)

只有在梯度幅值指标计算取值结果保持不变的情况下，深度学习算法才能对卫星遥感图像边缘区域内的特征参量进行准确检测。

3.4 双阈值计算

在对卫星遥感图像边缘进行检测时，图像特征参量的灰度变化较为明显，因此为使检测结果具备恒定性，应根据双阈值表达式对所选取检测区域进行阈值分割。双阈值就是从极大值、极小值两个角度，对待检测卫星遥感图像的边缘特征参量进行判别，在建立表达式条件时，则要求这两项指标的取值结果必须满足深度学习算法的约束条件[23-24]。设Tmax表示待检测卫星遥感图像边缘特征参量的极大性阈值参考条件，Tmin表示极小性阈值参考条件，W双向性标记系数。联立上述物理量，可将双阈值表达式定义为：

(15)

在深度学习算法的支持下，考量双阈值表达式的约束能力，从而实现对卫星遥感图像边缘的精准检测。

4 实例分析

本次实验在一台操作系统为Windows 10的笔记本电脑中进行，其内存为4 GB。以Matlab 2016a平台中完成模型仿真，选取三幅遥感图像作为本文的研究样本，如图3所示，对其展开研究。

图3 遥感图像研究样本

为充分验证所提方法的实用性，选取文献[3]基于方向和结构特征的检测方法为对比方法，进行对比实验。将选取的三幅遥感图像在保证清晰度的情况下，对其进行复制出来，以复制后图像作为对照组实验对象，将原图像作为实验组实验对象，分别对其进行边缘检测。待检测完毕后，选取信噪比、模糊噪点个数及图像清晰度为指标对比检测完毕后图像边缘检测质量。

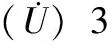
(16)

对于卫星遥感图像来说，边缘节点处信噪比指标的数值水平可用来描述模糊噪点对于图像清晰度的影响能力，从而反映出所选取检测方法的准确性水平。如上式所示，边缘节点处信噪比指标的数值越大，模糊噪点对于图像清晰度的影响程度越轻，即当前所选取检测方法的准确性水平较高；反之，若边缘节点处信噪比指标的数值较小，则表示模糊噪点对于图像清晰度的影响程度较重，即当前所选取检测方法的准确性水平较低。

所提方法、文献[3]方法检测后，先自适应划分DN值子区间,然后以一定百分比最小局部标准差的平均值估算每一DN值子区间对应的噪声大小,估算每一DN值子区间对应的信噪比，最后完成整幅图像的信噪比数值计算。获得卫星遥感图像边缘节点处信噪比指标(ψ)的数值变化情况，其对比如图4所示。

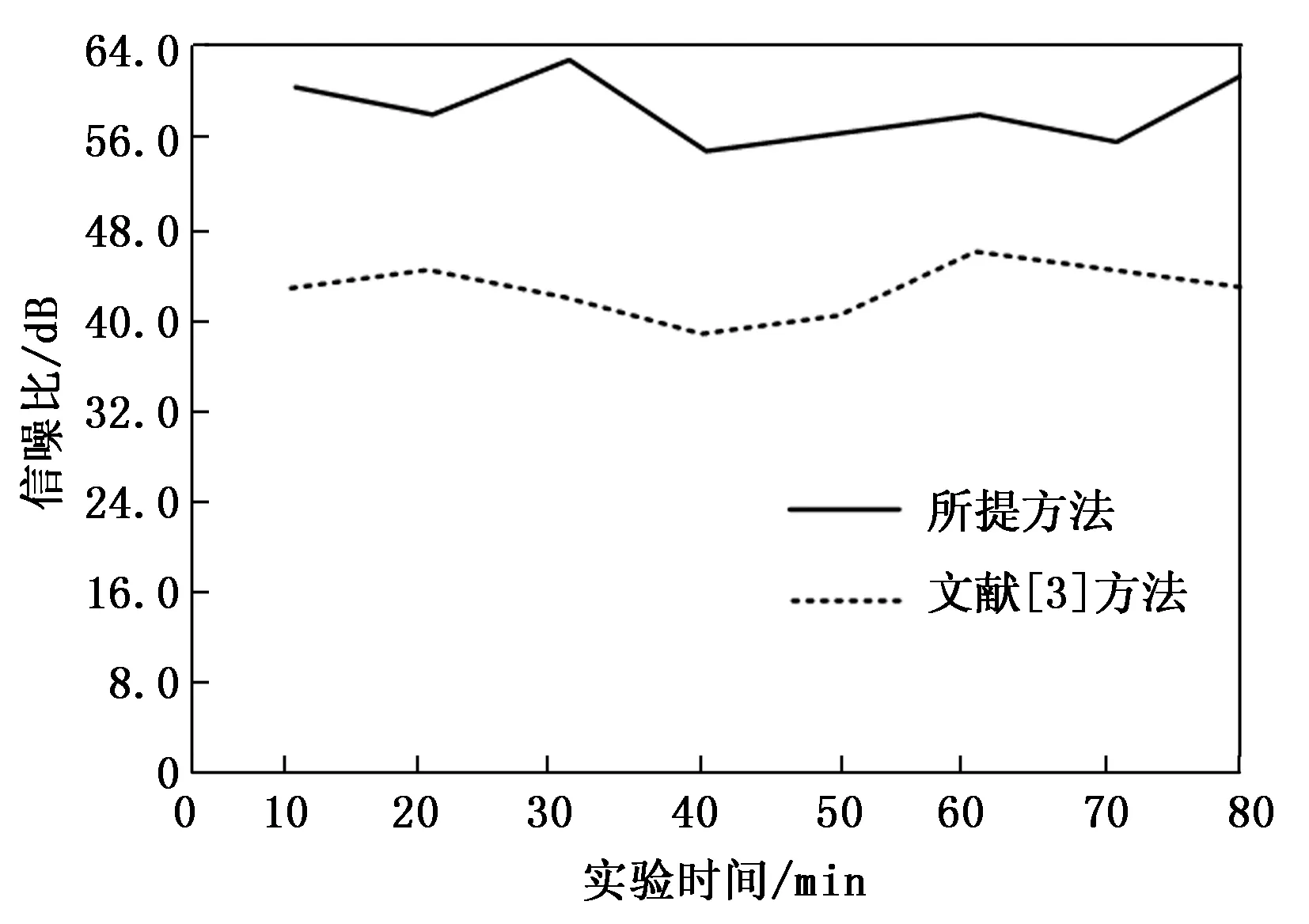
图4 信噪比数值

分析图4可知，随着实验时间的延长，两种方法获得的卫星遥感图像边缘节点处信噪比指标均呈现出来回波动的数值变化状态。当实验时间等于30 min时，实验组信噪比指标达到最大值62.7 dB，整个实验过程中，实验组信噪比数值的波动区间为55.1～62.7 dB，取得极小值时的实验时间为40 min；当实验时间等于60 min时，对照组信噪比指标达到最大值45.6 dB，整个实验过程中，对照组信噪比数值的波动区间为38.9～45.6 dB，取得极小值时的实验时间也为40 min；从平均值角度来看，实验组信噪比均值始终高于对照组。

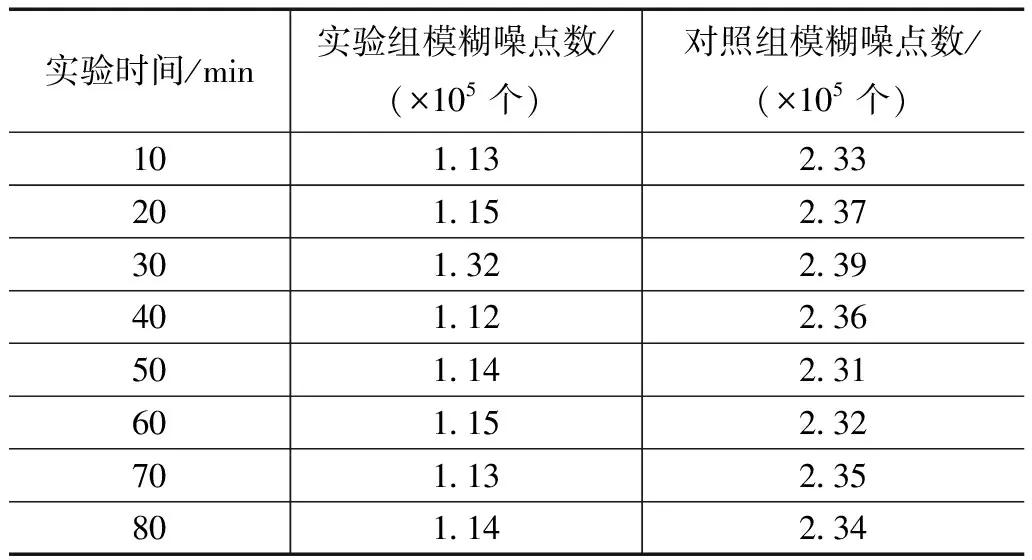
表1 模糊噪点个数值

分析表1可知，实验组模糊噪点个数相对较少，其最大值只能达到1.32×105个，与对照组最大值2.39×105个相比，下降了1.07×105个。

联合图4、表1及公式(16)，对实验组、对照组卫星遥感图像清晰度(R)指标进行计算。具体计算结果如表2所示。

表2 卫星遥感图像清晰度

分析表2可知，随着实验的延长，实验组、对照组卫星遥感图像清晰度指标R的数值变化趋势，符合来回波动的变化规律。对于实验组检测方法而言，当实验时间等于30 min时，其清晰度指标R的数值计算结果最大，达到了5.45×10-4；当实验时间等于50 min时，其清晰度指标R的数值计算结果最小，仅为4.91×10-4；两者之间的物理差值为0.54×10-4。对于对照组检测方法而言，当实验时间等于60 min时，其清晰度指标R的数值计算结果最大，达到了1.97×10-4；当实验时间等于30 min时，其清晰度指标R的数值计算结果最小，仅为1.75×10-4；两者之间的物理差值为0.22×10-4。整个实验过程中，实验组卫星遥感图像清晰度指标R的数值水平始终高于对照组。

综上可知，本次实验结论为：基于方向和结构特征的检测方法不能较好地促进卫星遥感图像边缘区域节点处信噪比指标的数值水平，且与之相关的模糊噪点个数值较大，这就导致最终所得的图像清晰度水平较小，无法满足实际应用需求；而基于深度学习的检测方法能够合力促进卫星遥感图像边缘区域节点处信噪比指标的数值水平提升，且与之相关的模糊噪点个数值相对较小，满足提升图像清晰度的实际应用需求。

5 结束语

新型卫星遥感图像边缘检测方法根据深度学习理论，完善了Softmax分类器，并以此为基础，对待测图像的边缘性特征节点进行卷积与池化处理，在已知尺度空间条件的前提下，该方法准确定义了特征点所处位置，并根据梯度信息熵指标的计算数值，求解一阶微分边缘算子与二阶微分边缘算子，进而得到完整的双阈值表达式。与基于方向和结构特征的检测方法相比，深度学习算法针对图像边缘节点处信噪比指标数值水平较低的问题进行了有效改进，可在避免模糊噪点对图像清晰度产生影响的同时，实现对卫星遥感图像边缘的精准检测。