钢筋混凝土深梁在冲击荷载作用下的动力响应分析

罗绪昌，蔺宝垚，张春霞

(1.济南市交通工程质量与安全中心，山东 济南 250002；2.交通运输部公路科学研究院，北京 100088)

0 引言

钢筋混凝土结构在服役期间，可能会遭受到各种极端荷载，如地震、爆炸和冲击等。与遭受静力荷载的钢筋混凝土结构不同，由于结构自身惯性和应变率效应的影响，其性能变得极其复杂，如在静力荷载作用下的梁为弯屈破坏，而在冲击荷载作用下却为弯剪破坏[1-2]。由于钢筋混凝土结构的动力特性较为复杂，对于其抗爆抗冲击性能的理解较为有限。

在诸多的钢筋混凝土结构中，钢筋混凝土梁也常常遭受到冲击荷载作用。一般而言，钢筋混凝土梁的冲击性能研究方法主要包括试验装置与试验方法、抗弯与抗剪设计方法和冲击荷载作用下动力响应研究[3-5]。Bentur,Saatci等[6-7]基于落锤冲击试验结果，指出梁在冲击初期加速很大，从而产生较大的惯性力抵抗冲击力。Huges等[8]基于试验结果，提出了钢筋混凝土梁在冲击过程中的能量耗散行为。Kishi等[9]基于对在不同冲击速度的钢筋混凝土梁的冲击试验结果，指出对于相同承载力和冲击速度的钢筋混凝土梁，其自身截面和配筋等的变化，不会影响支座反力和跨中位移响应。Fujikake等[10]揭示了纵向钢筋配筋率对其抗冲击性能的影响机制。李砚召等[11]基于无黏结预应力梁进行了试验研究，指出了其动态响应规律。

由于钢筋混凝土梁的截面尺寸不同。其抗冲击性能也将形成明显差异，目前对普通钢筋混凝土梁在动力荷载下性能的研究已经较多，但是对深梁的研究还十分欠缺，根据美国混凝土建筑结构规范ACI318-08，采用拉压杆模型进行设计计算，净跨与梁高之比为3，对其抗冲击性能的理解还十分有限。Adhikary等[12]开展了对钢筋混凝土深梁在动力荷载下的抗剪强度及性能的研究，发现深梁的承载力随加载速率的提高而提高，但不同的加载速率对破坏形态没有影响。Ferrer等[13-15]基于深梁的冲击试验，指出冲击速度是影响钢筋混凝土深梁破坏形态的关键因素，并且阐明了冲击力峰值与冲击速度、最大跨中位移和跨中残余位移与冲击速度在不发生严重剪切破坏时均满足近似线性关系，同时混凝土结构的惯性和材料应变率的影响，导致钢筋混凝土结构的抗冲击能更加得复杂。

综上所述，由于材料应变率效应和惯性力的影响，钢筋混凝土在冲击荷载下的内力响应较为复杂，但是目前对钢筋混凝土深梁的抗冲击性能研究较少。本研究在已有试验的基础上，对简支钢筋混凝土深梁进行了多参数分析，包括冲击速度、冲击位置和混凝土的强度等因素，研究冲击力和位移时程曲线的变化规律，对比不同条件下的剪力响应和破坏模式。

1 钢筋混凝土模型验证

1.1 数值模型

许斌等[16-18]对钢筋混凝土深梁在简支条件下进行了侧向冲击试验。本研究以2BD2模型为物理验证模型。试验中梁的边界条件采用钢板和钢辊结合的方式表示简支条件，在梁的跨中位置进行落锤冲击。钢筋混凝土深梁的截面具体尺寸为170 mm ×620 mm，净跨度为1 860 mm，其具体配筋和相关尺寸如图1所示。

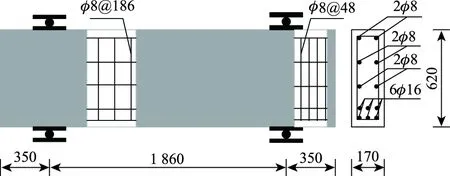
图1 深梁2BD2的尺寸及配筋(单位：mm)Fig.1 Dimensions and reinforcement of deep beam 2BD2 (unit: mm)

采用有限元软件LS-DYNA对深梁进行冲击作用分析，该软件被广泛应用于分析钢筋混凝土结构的冲击和爆炸问题。采用八节点六面体模拟钢筋混凝土，网格尺寸为10 mm。通过将钢筋与混凝土划为共节点单元，忽略钢筋与混凝土之间的黏结滑移，钢筋采用梁单元(BEAM161)。钢板、落锤和钢辊轴依旧采用实体单元表示，钢筋混凝土深梁的有限元模型的详图如图2所示。为了保持试验和数值的一致性，边界条件与试验都为简支，即在外侧钢板施加固定约束。各个试件之间的接触方式采用面面接触，通过对落锤施加初速度与梁进行冲击。

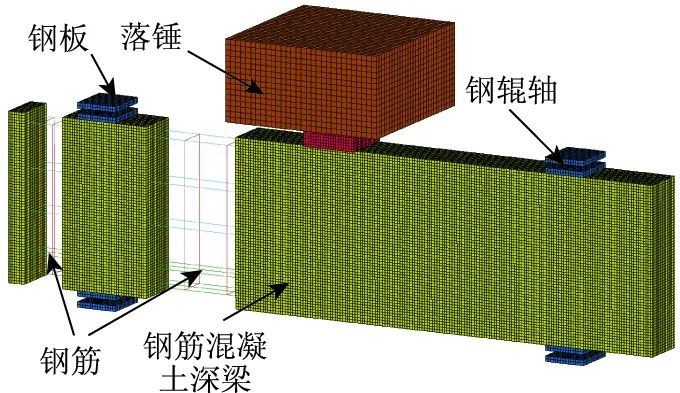
图2 深梁的有限元冲击模型Fig.2 Finite element impact model of deep beam

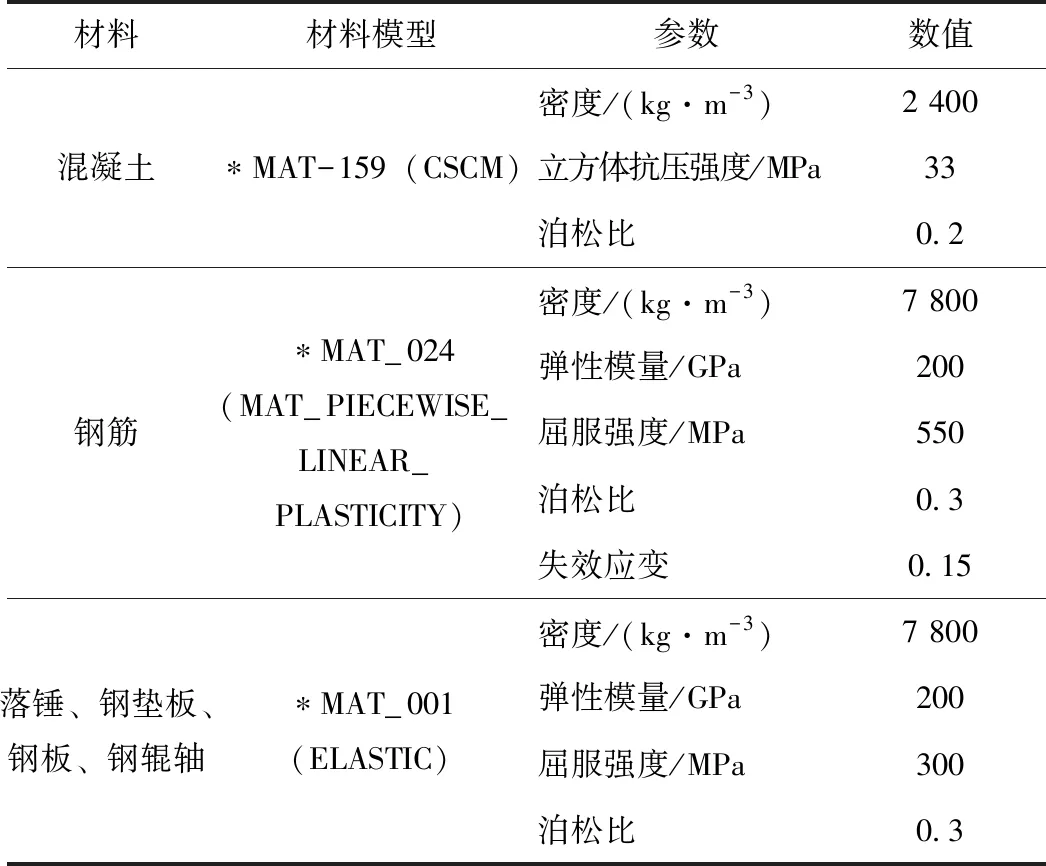
表1 材料模型参数Tab.1 Parameters of material model

在冲击荷载作用下的混凝土本构模型，本研究采用*MAT-159(CSCM)，混凝土的轴心抗压强度强度为33 Mpa，通过用户自定义参数的方式定义混凝土的属性。混凝土的应变率效应按照CEB-FIP规范考虑，当最大主应变超过0.1时混凝土单元发生侵蚀。采用*MAT_024本构模型表示钢筋在冲击荷载下的力学性能，其屈服强度为550 MPa，弹性模量为200 GPa。考虑到在冲击荷载下钢筋的力学性能会改变，采用式(1)确定钢筋的应变率。采用*MAT_001表示落锤、钢板和钢辊轴等本构模型，其参数与试验相同。表1为钢筋混凝土深梁的数值模型材料参数。

(1)

为了研究钢筋混凝土深梁的抗冲击性能，先后对不同冲击速度、不同混凝土强度和冲击位置的钢筋混凝土深梁进行研究，其具体分析方案如表2所示。

表2 深梁冲击工况Tab.2 Impact condition of deep beam

1.2 数值模型验证

图3和图4分别为在冲击荷载下钢筋混凝土深梁的试验和数值破坏模式。从图3可知，试验和数值模型在冲击荷载下跨中产生了大量的弯曲裂缝，并且在两侧形成临界弯剪裂缝，梁受到冲击的区域由于落锤的动能较大，使得局部产生较大损伤。从图4可知，二者的冲击力时程曲线和梁的跨中位移时程曲线相近，试验和数值的冲击力峰值分别为1 838 kN和2 053 kN，主要原因是因为在数值模拟中，接触面光滑平坦，且忽略了空气中的阻尼。试验和数值的峰值位移分别是32.2 mm和30.8 mm，二者相差4%。

本研究建立的钢筋混凝土深梁在冲击荷载下的破坏形态、冲击力和位移响应等与试验结果相近，较好地再现了破坏过程，验证了本建模方法的有效性。

图3 试验和数值的破坏模式Fig.3 Test and numerical failure modes

图4 数值模型和试验的位移响应Fig.4 Displacement responses of numerical model and test

2 冲击结果分析

2.1 冲击力分析

在冲击荷载作用下，由于冲击的能量不同，结构自身属性的区别和接触刚度的差异，钢筋混凝土在冲击荷载下的冲击力时程曲线具有明显区别。图5展示了不同冲击工况的冲击力时程曲线。从图5(a)可知，随着落锤冲击速度的增大，冲击力的峰值逐渐增大，冲击力峰值的时刻逐渐减小，由于钢筋混凝土梁的反弹发生二次碰撞力之间的差值也逐渐增大。随着混凝土强度的增大，钢筋混凝土深梁的局部刚度和整体刚度逐渐提高，因此，混凝土强度增大使得深梁在相同冲击荷载下的冲击力峰值逐渐增大，如图5(b)所示。从图5(c)可知，冲击力位置的不同，会影响钢筋混凝土深梁受到的冲击力，主要是由于冲击位置改变使得钢筋混凝土深梁的局部惯性发生变化，其中冲击位置为跨中的工况冲击力峰值最大。

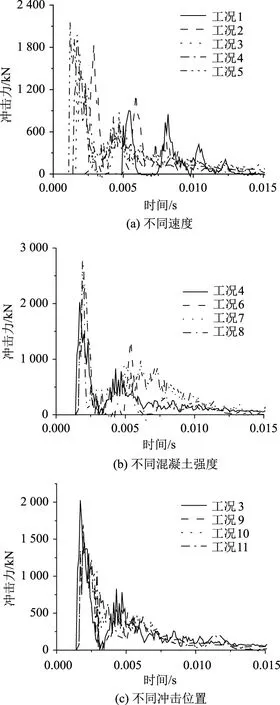
图5 冲击力时程曲线Fig.5 Curves of impact force time history

2.2 位移分析

图6展示了不同冲击速度下的跨中位移。可以看出，冲击能量对深梁的跨中位移的最大值和残余位移影响较大，且随着冲击能量的增大，跨中位移与其呈现正相关的关系。值得注意的是，随着混凝土强度的提高，深梁的局部刚度和整体刚度都逐渐提高，因此，跨中位移的最大值和残余位移随着混凝土强度提高逐渐减小，如图7所示。

图6 不同冲击速度的深梁跨中位移Fig.6 Mid-span displacements of deep beam under different impact speeds

图7 不同混凝土强度的深梁跨中位移 Fig.7 Mid-span displacements of deep beam under different concrete strengths

图8描绘了不同冲击位置的冲击中心点的位移时程曲线。由于从跨中到支座的距离越近，受到边界条件的影响越显著，因此，随着冲击位置逐渐靠近支座，冲击点的峰值位移和残余位移逐渐下降。

图8 不同冲击位置的深梁冲击区域位移Fig.8 Displacements of Impact area of deep beam at different impact positions

2.3 剪力响应

图9 不同截面的剪力时程曲线Fig.9 Curves of shear force time history on different sections

图10 深梁的截面位置Fig. 10 Sections of deep beam

图9为工况1不同截面的剪力时程曲线。考虑到结构对称性，主要选取支座截面、冲击区域与支座的中线截面、冲击区域截面(下同)，如图10所示。从图9可知，深梁截面5-5的剪力峰值最大，最小的为支座处截面，比较明显的是截面的剪力受到冲击力的影响较大，其响应形式与冲击力时程曲线相近。

图11为钢筋混凝土深梁的剪力沿着长度方向的分布。从图11(a)可知，随着冲击速度的增大，深梁的剪力分布逐渐增大，但是在跨中区域，当冲击速度达到6 m/s时，深梁的剪力值不在增大，这主要是冲击区域梁已经不再具有承担更大的剪力作用。图11(b)为不同混凝土强度的剪力包络曲线，随着混凝土强度的增大，沿着长度方向分布的剪力逐渐增大。

图11 沿着梁长度方向的剪力分布Fig.11 Distribution of shear forces along beam length

2.4 破坏模式

图12为不同冲击速度作用下钢筋混凝土深梁的塑性应变分布。从图12可知，冲击速度的不同明显影响梁的塑性分布趋势，随着冲击速度的增大，梁的损失程度逐渐增大，且裂缝分布也逐渐密集。当冲击速度为2 m/s时，跨中形成少许的竖向裂缝，以两端支座和冲击位置形成对称的剪切斜向裂缝。当冲击速度为9 m/s时，冲击区域的损失较大，梁的裂缝分布较为密集，跨中弯曲裂缝接近梁顶。深梁的破坏模式都为弯剪破坏，但是随着冲击速度的增大，梁的破化模式受剪力影响更加明显。

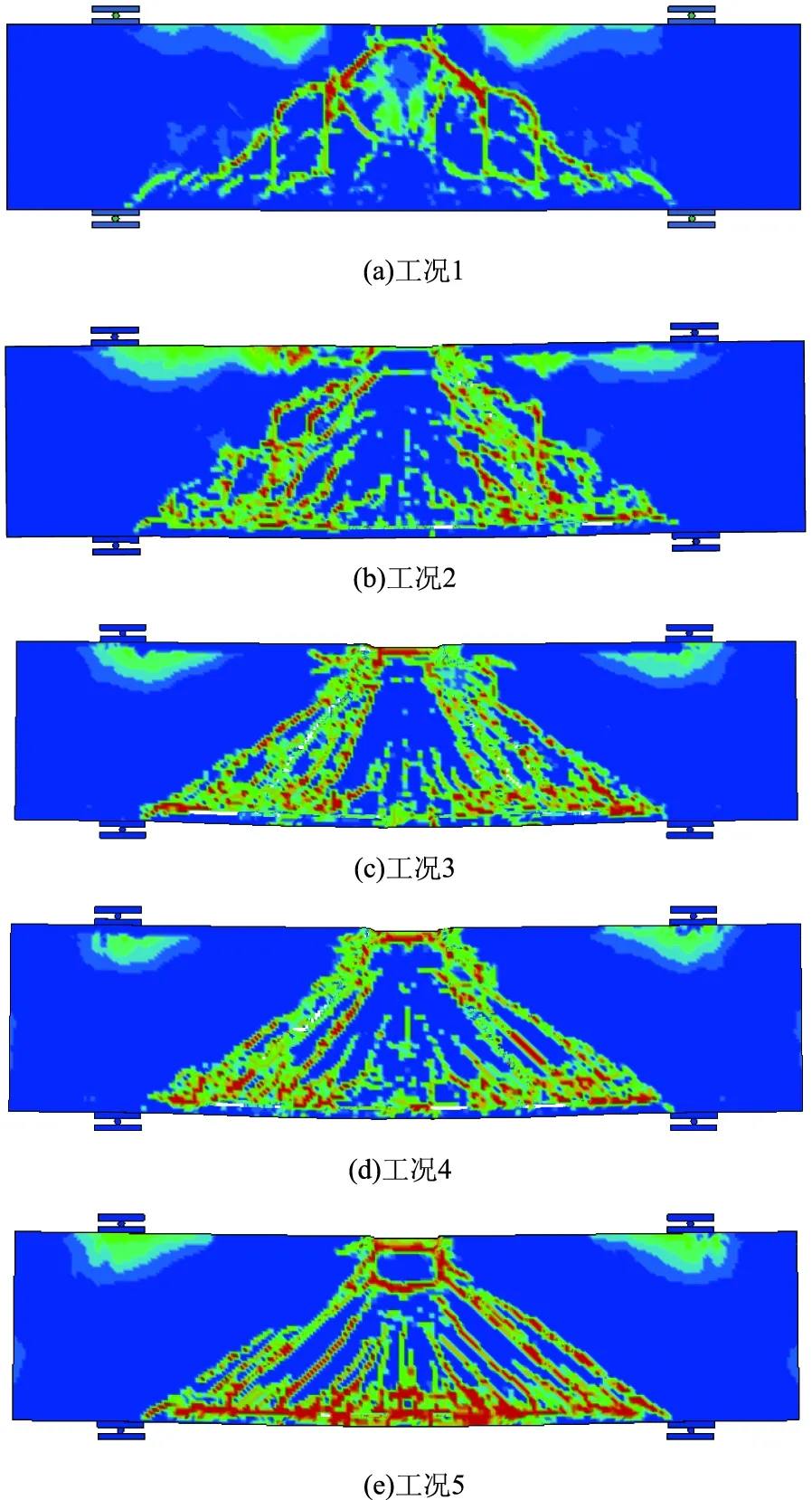
图12 不同冲击速度的深梁塑性应变Fig.12 Plastic strains of deep beam at different impact speeds

图13为在相同冲击速度下的不同混凝土强度深梁的塑性应变分布。提高钢筋混凝土梁混凝土的强度，梁的局部刚度会略有增大，因此在冲击区域可以承担更多的荷载，其损伤程度逐渐降低。值得注意的是，随着混凝土强度的提高，深梁的裂缝分布形式逐渐发生改变，即裂缝密度逐渐下降，且受弯曲影响更加明显。

图13 在4 ms时刻不同混凝土强度的深梁塑性应变Fig.13 Plastic strains of deep beam at different concrete strengths at 4 ms

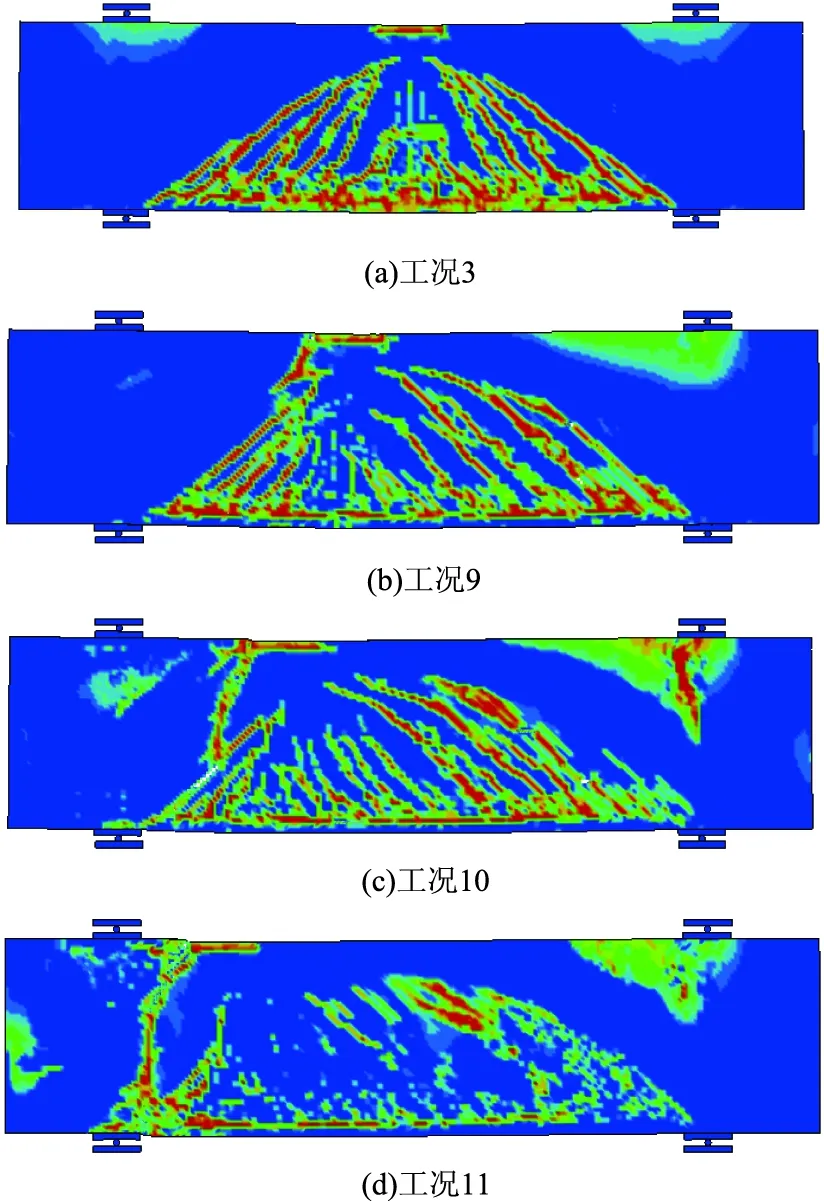
图14 在4 ms时刻不同冲击位置的深梁塑性应变Fig.14 Plastic strains of deep beam at different impact positions at 4 ms

图14为在相同冲击速度下的不同冲击位置的梁塑性应变分布。如前文所揭示，由于冲击位置的逐渐向支座处逐渐移动，使得其内力分布形成区别，从而使得深梁的塑性应变也会不同。当冲击位置位于梁的跨中区域时，深梁的塑性应变分布形式基本呈现对称现象。当距离跨中距离为400 mm时，深梁在右侧支座处出现了较深的剪切裂缝，这主要是由于钢筋混凝土梁在冲击位置向下弯曲，而梁的远端受到了支座的限制作用而形成较大的反作用力，因此形成了较深的剪切裂缝。在靠近冲击区域的支座，形成了冲击区域与支座的贯通剪切裂缝。当距离跨中为600 mm时，左侧支座处的剪切裂缝更加明显，但是梁的整体塑性损失较少。

4 结论

本研究首先建立了钢筋混凝土深梁的数值模型，通过试验验证了数值建模方法的可靠性，然后拓展了研究内容。具体结论如下：

(1)冲击力时程曲线受到落锤冲击能量的影响较大，混凝土强度提高使得冲击力峰值逐渐增大。

(2)深梁的跨中位移与冲击能量呈现线性关系，且随着混凝土强度的提高，峰值位移和残余位移逐渐下降。

(3)深梁的剪力响应受到冲击位置的影响，在跨中冲击荷载作用下，深梁的剪力响应以中线为轴呈现对称分布。深梁在冲击区域形成了高剪力作用。

(4)冲击速度越大，深梁的裂缝分布越密集，且受剪影响越明显。混凝土强度提高使得梁的损伤越小。此外，冲击位置越靠近支座，深梁的损伤越小。