基于车-桥响应连续小波变换的桥梁无模型损伤识别方法
安 宁,和海芳,马 瑞,蔺宝垚
(交通运输部公路科学研究院,北京 100088)
0 引言
由于历史原因,一些老桥的设计资料缺失了。当对这些老桥进行损伤识别时,大部分基于有限元模型的损伤识别方法都会失效,只能使用无模型的损伤识别方法。
Yang和Lin等[1-2]在 2004 年提出用移动车辆动力响应来识别桥梁的频率,并进行了实桥试验验证。2006 年,Bu和Li等[3-4]通过分析车辆动力响应的灵敏度来进行损伤识别。Kim等[5]基于车-桥耦合运动方程得到了拟静力公式,并提出了用单元刚度指数来识别损伤。Obrien等[6]对响应使用经验模态分解识别损伤。Nguyen等[7]利用小波变换系数识别出了损伤的位置。Khorram等[8]证明了小波对移动位置响应比对固定位置响应更加敏感。聂振华等[9]提出了联合移动主成分分析与传递熵的识别方法进行桥梁结构损伤定位,此方法无需建立结构有限元模型作为基础。张彬[10]利用希尔伯特变换获得瞬时幅值平方,并将其作为损伤检测的关键指标。
利用车辆荷载下的桥梁响应来识别结构损伤,可以不中断交通,并且更符合实际工作状态,有利于实现桥梁的长期在线监测,而且不需要结构的有限元模型,具有很大的优势。本研究提出了一种基于车桥动力相互作用来识别桥梁损伤的方法。
1 基于集中扭转弹簧损伤模型的车桥动力分析
1.1 有裂缝简支梁模型
以简支梁为例,当跨径为L、梁高为H的简支梁在距离梁左端s处存在高度为h的裂缝时,可以把梁的裂缝模拟成扭转弹簧[11-13],通过这个弹簧连接起裂缝两端的梁段,模型如图1所示。

图1 有裂缝简支梁模型Fig.1 Simple supported beam model with crack
扭转弹簧的刚度可表示为kc=1/C[14],其中:
37.14(h/H)2-35.84(h/H)3+13.12(h/H)4],
(1)
式中,C为扭转弹簧刚度的倒数;EI为梁抗弯刚度。
梁的振型可以用下式表示:
(2)
式中,x为距梁左端的距离;φA,φB分别为梁段A,梁段B的振型;A1,B1,C1,D1,A2,B2,C2,D2为待定系数;a为自定义参数,a4=ω2ρA/EI。
很容易得到梁的边界条件为:
(3)
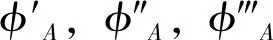
将式(2)代入式(3),为使此方程组有非平凡解,则方程系数矩阵的行列式为0,即:
(4)
式中,s1=sin(aL);c1=cos(aL);sh1=sinh(aL);ch1=cosh(aL);s2=sin(as);c2=cos(as);sh2=sinh(as);ch2=cosh(as);η=CEIa。
解式(4)可得到a,并解得待定系数Ai,Bi,Ci和Di(i=1,2),进一步可以求出梁的振型φ(x)。
1.2 移动车辆作用下损伤梁和车辆的动力响应
使用弹簧-阻尼-质量系统模拟车辆,该系统由一个刚度为k的弹簧和一个阻尼为c的阻尼器连接起质量M1和M2,如图2所示。
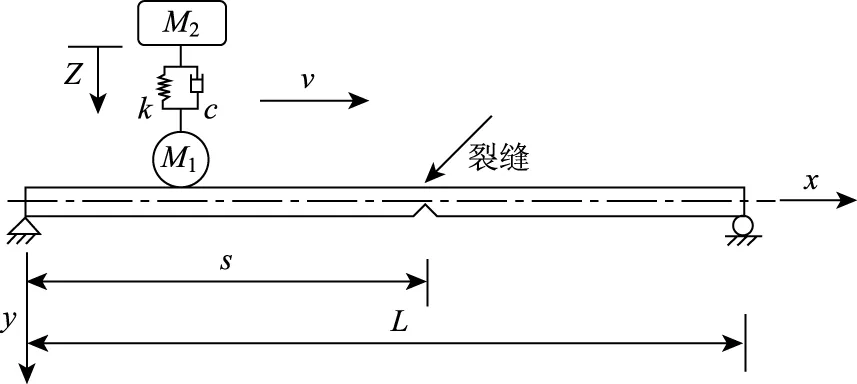
图2 车-桥振动模型Fig.2 Vehicle-bridge vibration model
假设车辆在梁上保持匀速行驶,车速为v。当车辆在梁上行驶时间为t时,桥梁距左端x处的竖向位移为y(x,t),簧下质量M1的竖向位移为y(vt,t),簧上质量M2的竖向位移为Z(t)。可以得到车-桥耦合振动方程为:
(5)

对式(5)求解,可以得到桥梁和车辆的时域响应。
2 基于连续小波变换的损伤识别原理
对信号x(t)进行小波变换后可以得到:
(6)
当信号x(t)发生突变时,x(t)*θa(t)会出现拐点,此时Wx(a,t)取得其极大值,所以找到小波系数取极大值的点,也就找到了信号的突变点。大量实践也证明,可以通过对信号进行连续小波变换来检测这个信号是否为奇异性信号[15-18]。
一般来说,当车辆经过桥梁的一个损伤点时,桥梁各处和车辆的动力响应都会在此处发生突变。所以可以记录桥梁某处或者车辆的动力响应,然后对其进行连续小波变换,如果可以找到小波系数取极大值的点,也就找到了信号的突变点,也就确定了桥梁的损伤位置。
3 算例
3.1 不考虑噪声影响
以一个跨径50 m的简支梁桥为例,根据裂缝的数量、位置和深度设置5种工况,如表1所示。
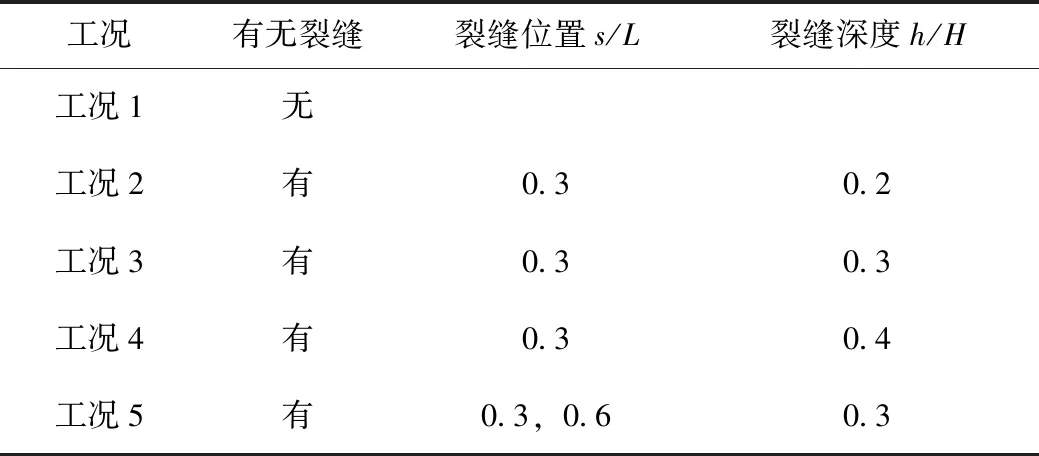
表1 裂缝工况设置Tab.1 Setting of crack working conditions
计算一辆车通过桥梁时的动力响应,取M1=5 t,M2=35 t,k=1.5×106kN/m,c=160 kN/(m/s),v=10 m/s。
不考虑噪声的影响,分别计算工况1~工况4时梁的跨中位置和车辆的簧上质量的竖向位移,结果如图3所示。可以看出,当桥梁上出现裂缝时,车辆和桥梁的动力响应变化并不大,所以不能直接通过时域响应来判断桥梁是否存在裂缝。
使用Mexican Hat小波分别对车辆和桥梁的竖向位移时程进行连续小波变换,尺度为82,小波系数如图4所示。
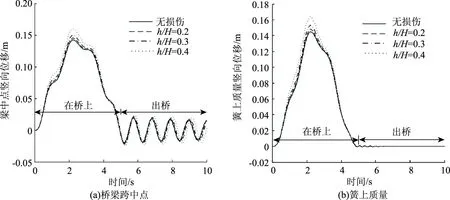
图3 车-桥位移Fig.3 Vehicle-bridge displacement

图4 小波系数Fig.4 Wavelet coefficients
分别对桥梁和车辆的振动响应信号进行连续小波变换,可以检测振动响应信号的奇异性,从而确定裂缝位置。裂缝深度越大,裂缝处的小波系数值也越大,识别效果也越明显。
3.2 小波尺度的影响
其他参数保持不变,尺度分别取1~500之间的整数值,使用前节的方法可以得到500个被识别出的裂缝可能位置,绘制裂缝可能位置与小波尺度的关系如图5所示。
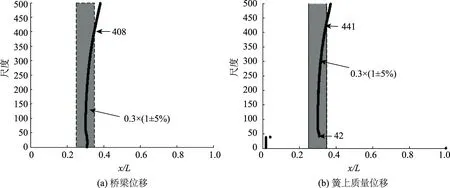
图5 通过小波系数模极大值位置识别的损伤位置Fig.5 Identified damage location using wavelet coefficient modulus maximum position
当使用桥梁位移响应进行检测时,识别出的裂缝可能位置均分布在实际位置附近,小波尺度在1~408之间时,识别误差在5%以内。当使用车辆位移响应进行检测,小波尺度在42~441之间时,识别误差在5%以内。
对工况5进行分析,此时梁上有2处裂缝,识别出的裂缝可能位置如图6所示。从图中可以看出,连续小波变换方法对2处裂缝的工况依然有效。

图6 使用位移响应识别的桥梁双裂缝Fig.6 Identified bridge double-crack using displacement response
3.3 噪声的影响
为振动响应添加5%的噪声,其他参数保持不变,使用前节的方法可以得到如图7所示的识别结果。

图7 有噪声时识别的损伤位置Fig.7 Identified damage location when noising
可以看出,振动响应添加5%噪声后,仍然能清晰分辨出变异点的位置,但裂缝识别效果变差。另外即使桥梁端部位置没有裂缝,信号在桥梁端部位置也出现了变异,所以该方法不能很好地识别桥梁端部是否真实存在裂缝。
3.4 车辆参数的影响
为了解车辆参数对识别结果的影响,分别按照车速、质量、刚度等参数设置了工况6~工况20,如表2~表5所示。各工况除了考察参数不同外,其他参数均保持一致。

表2 车辆速度工况Tab.2 Working conditions of vehicle speed

表3 车辆质量工况Tab.3 Working conditions of vehicle mass

表4 车辆刚度工况Tab.4 Working conditions of vehicle stiffness

表5 车辆阻尼工况Tab.5 Working conditions of vehicle damping
计算结果如图8所示,可以看出不同车辆参数对该识别方法的影响:
(1)车速较低时,小波系数波动较小,变异点更加明显,较低的车速有利于损伤的准确识别。
(2)车辆质量越大,裂缝处的小波系数越大,识别效果越好。
(3)车辆的刚度和阻尼对识别结果的影响较小。

图8 不同参数对识别结果的影响Fig.8 Influence of different parameters on identification result
4 结论
本研究提出了一种基于车-桥耦合运动时程空间小波分析的桥梁结构损伤检测技术,建立了简支梁在移动弹簧质量单元作用下的模型,并推导了系统的运动方程。利用车辆荷载下的桥梁响应来识别结构损伤,可以不中断交通,有利于实现桥梁的长期在线监测,并且不需要结构的有限元模型,具有很大的优势。本研究得到如下几点结论:
(1)使用车-桥动力响应,不需要建立桥梁的有限元模型就可以较好地识别桥梁的单裂缝或双裂缝。
(2)考虑噪声时仍然可以得到较好的识别效果,但当裂缝位于桥梁端部时,可能会造成误判。
(3)当车辆较重、车速较低时识别效果较好,车辆的刚度和阻尼对识别结果的影响较小。

