两阶段混合引导的偏好多目标优化算法
梁海娜,王宇嘉,林炜星,陈万芬
(上海工程技术大学 电子电气工程学院,上海 201620)
0 引 言
多目标进化算法(multi-objective evolutionary algorithms, MOEAs)是一种结合生物进化理论和随机搜索机制来求解多目标优化问题(multi-objective optimization problem, MOP)的算法,被广泛应用于数据挖掘[1]、路径规划[2]、过程控制与操作优化[3]、交通与物流系统优化[4]等领域。
在实际应用中,由于个人偏好或者实际生产需求,决策者可能只需要Pareto解集的部分解个体供其决策,不需要算法求解整个非支配解集。因此,在算法求解过程中,加入偏好信息协助算法搜索偏好解集,成为多目标优化领域的一大研究热点。通过加入偏好信息,一方面提高了算法的搜索效率,减少对多余目标空间的搜索;另一方面也减轻了决策者的选择压力。
目前,研究者已经提出多种基于偏好信息的多目标进化算法。J. Molina等[5]提出了g-占优的g-NSGAII算法,该算法可以缓解候选解支配选择压力,但偏好点所处目标空间位置会影响算法的优化性能;邱飞岳等[6]结合g-占优和正负偏好信息,提出了双极偏好支配方法,在种群个体间定义了一种更严格的支配关系,但是当决策者提供的正偏好点距离前沿较远,而负偏好点距离前沿较近时,种群易陷入局部最优;A.Jaszkiewicz等[7]采用了结合光速搜索的思想,没有考虑负偏好信息,在解决高维优化问题上性能不足; P.Korhonen等[8]提出了一种可视化互动方法, 此种方法需要决策者进行交互,增加了决策者的选择压力;文献[9]结合Pareto支配策略,定义了一种r-dominance支配关系的r-NSGAII算法,当参考点距离真实前沿较远时,偏好解集远离真实前沿面,收敛性较差;文献[10]基于分解算法思想,结合权重迭代求解偏好多目标优化问题;郑金华等[11]结合了个体间偏好角度思想,提出了一种基于角度的AD-NSGA-II算法;文献[12]提出一种基于指标的交互式算法,这些研究成果结合了偏好区域引导思想来求解偏好多目标优化问题。
上述研究一般采用单一偏好信息引导寻优,没有从多角度充分利用偏好信息指导算法迭代,导致算法易受偏好点位置影响或不能控制偏好解集范围,给决策者带来决策负担。因此,本文结合偏好点和偏好向量这2种偏好信息,提出了一种两阶段混合引导的偏好多目标优化算法,采用NSGA-II算法[13]框架,分阶段调整偏好引导方式,将g-占优和偏好向量引导相结合,算法充分利用了偏好信息。实验结果表明,本文所提算法能够使得种群快速收敛到偏好区域,获得合适规模的偏好解集。
1 相关概念
1.1 多目标优化问题
多目标优化问题通常可以表示成如下最小化问题
minF(x)=min{f1(x),f2(x),…,fm(x)},x∈Rn
(1)
(1)式中:x=(x1,x2,…,xn)为决策空间Rn中的一个决策变量;n为决策变量的维度;fi(x)为目标空间Rm中的第i个目标向量,其中,i=1,2,…,m,m为优化问题目标个数;gi(x)≤0对应此类优化问题的线性p个不等式约束条件;hj(x)=0则对应优化问题的q个线性等式约束条件。在求解多目标优化问题时,Pareto相关定义如下[14]。
1)Pareto支配。选取决策空间中任意2个决策变量xa,xb∈Rn,其中,xa=(xa1,xa2,…,xan),xb=(xb1,xb2,…,xbn),当且仅当满足如下2个条件,定义xaPareto支配xb,记做xaxb。
①fi(xa)≤fi(xb),∀i∈{1,2,…,m};
②∃j∈{1,2,…,m},fj(xa) 2)Pareto最优解。在决策空间中的xa∈Rn,表示MOP的一个可行解,当满足(2)式,则称xa为此优化问题的Pareto最优解。 ┐∃x∈Rn,xxa (2) 3)Pareto最优解集。多目标优化问题的Pareto最优解集的定义为 P*={x∈Rn|┐∃xd∈Rn,xdx} (3) Molina等提出了g-dominance[5]策略,该策略根据决策者提供的偏好点,定义一种新的个体间支配关系,使得个体之间的支配关系变得缓和,目标空间得到了偏好和非偏好区域的划分,增强了传统Pareto支配算法的种群个体支配排序选择压力。 若g为决策者偏好点,设y为目标空间中任意一个目标向量,定义flagg(y)为 (4) 根据flagg(y)的定义,对于2个目标向量ya,yb∈Rm,如果下面条件之一成立,称yag-支配yb。 ①flagg(ya)≥flagg(yb); ② 若flagg(ya)=flagg(yb),需要满足任意yai≤ybi(∀i=1,…,m),且至少存在一个i使得yai 快速非支配排序遗传算法(NSGA-II)是多目标进化优化领域应用较广泛的遗传算法之一。该算法在传统遗传算法框架上引入精英选择策略和快速非支配排序方法,具有求解效率高、优化解集收敛性好的优势。因此,本文采用此算法框架加入偏好引导机制,求解偏好多目标优化问题。偏好信息表示如图1所示,其中,p为偏好点,F1和F2是归一化目标函数值。 图1 偏好信息表示示意图Fig.1 Diagram of preference information representation 定义1(偏好点) 决策者对每个目标的优化期望值所构成的目标值集合为目标空间的一个偏好点,通常记作p(fp1,fp2,…,fpm)。 定义2(个体偏好距离) 在目标空间中,一般将经过原点和偏好点的向量定义为偏好向量,目标空间偏好区域划分示意图如图2所示,其中,Op(原点O和p点的连线)即为偏好向量。 对于种群中的任意个体xj,j=1,2,…,N,N为种群规模,其在目标空间中映射的目标向量为yj,表示为 yj=(f1(xj),f2(xj),…,fm(xj)) (5) 将种群中任意个体xj对应的目标向量yj到偏好向量的垂直距离定义为个体xj的偏好距离,记做Dis(xj),其计算方法表示为 j=1,2,…,N (6) 根据(6)式,图2中线段y1H的长度即为种群个体x1的偏好距离。 图2 目标空间偏好区域划分示意图Fig.2 Diagram of objective space preference area division 定义3(偏好半径) 为得到满足决策者偏好合适范围的偏好解集,设定偏好距离的上界限,定义其为偏好半径,记作R。 基于g-占优引导方式算法优化前期,候选解集中被偏好点Pareto支配的个体所占比例较大,且这些个体之间根据Pareto非支配进行排序选择,偏好收敛性不强。为提升算法初期种群偏好收敛速度,本文提出一种基于g-支配动态调整偏好区域界限策略。 首先,根据g-占优的定义可知,算法优先选择flagg值为1的个体,即在Pareto意义上支配偏好点和被偏好点支配的个体。为了更好地区分偏好区域内的个体,挖掘种群潜在的偏好信息,指导种群朝着偏好区域进化,本文将偏好区域做进一步划分,划分规则表示为 (7) 此划分规则将支配偏好点的个体定义其flagp值为1,而被偏好点支配的个体定义其flagp值为-1,其余个体定义其flagp为0。通过此种划分规则,目标空间区域被划分为4个部分,见图2。 然后,根据种群分布情况调整偏好界限,对采用g-占优得到的候选种群P,通过以上偏好区域划分规则,标记个体的flagp值。选择出flagp为-1的个体进行临时存档,并记其个数为num,通过(8)式计算该档案内个体数占种群总体的比例ratio-1。当该指标满足决策者指定范围时,对档案执行(9)式计算偏好区域界限pnew。 (8) pnew=(pnew1,pnew2,…,pnewm) (9) 偏好区域界限动态调整方法伪代码如算法1所示。 算法1偏好界限动态调整策略 INPUT:基于g-占优得到的种群P,决策者偏好点 p(fp1,fp2,...fpm),种群规模N; OUTPUT:pnew,ratio-1; 1.flagp=zeros(N,1)//初始化种群个体flagp值; 2.for eachxj∈P, do 3.if all(fpi≤fiXj) then 4.flagpj←-1//被偏好点支配的个体flagp赋值为-1; 5.else if all(fpi≥fiXj) then 6.flagpj←1//支配偏好点的个体flagp赋值为1; 7.elseflagpj=0 8.end if 9.end for 10.flagpj为-1的个体数量记为num; 11.根据(8)式计算ratio-1; 12.根据(9)式计算pnew。 最后,根据计算所得偏好界限,定义位于界限之内的个体偏好支配该界限之外的解,同时界限之内的个体根据g-支配策略非支配排序,界限之外的个体以Pnew为偏好点采用g-支配排序策略,使得靠近偏好点边界的候选解支配等级降低被舍弃,种群偏好收敛性能得到一定的提升,个体之间偏好区域界限支配策略伪代码如算法2所示。 算法2偏好区域界限支配策略 OUTPUT:Palt; 1.对种群P执行选择、交叉、变异策略,得到子代种群P1; 2.P=P∪P1//种群合并 3.for eachxj∈P, do 4.if all(fiXj≤fPnewi) then 6.else 8.end if 9.end for 14 else 16.P=Palt 17.end if。 2.3.1 偏好向量的设定 多数研究成果中将偏好点和原点的连线作为偏好向量[15],由于真实前沿和偏好点的位置关系未知,采用此种偏好向量为偏好信息载体,可能会引导算法朝着远离偏好区域进化。另外,随着算法迭代次数的增加,种群越来越能表征决策者的偏好信息,因此,本文根据种群进化过程,提出一种动态偏好向量的定义,首先计算当前种群个体对应的目标向量和偏好点的欧氏距离,记做Distance(xj|p),找出欧氏距离最小的解个体,记为xdirec,将其和偏好点的连线作为此时的偏好向量,计算方法表示为 i=1,2,…,m,j=1,2,…,N (10) (11) 2.3.2 偏好向量支配策略 决策者总是希望得到满足偏好范围的非支配解集,供其做出决策选择。但通常基于偏好点的引导方式不能控制解集偏好范围,使得优化结果得到过多非支配解,给最终决策带来决策选择压力。为控制偏好解集规模,本文结合偏好向量和决策者提供的偏好半径,对目标空间进行新的偏好区域划分,同时对种群个体采取新的偏好支配排序方法,增强种群选择压力。根据个体的偏好距离和偏好半径大小的关系,对目标空间进行相应的偏好区域划分,表示为 (12) (12)式中:R表示偏好半径,是决策者事先提供的定值;Dis(xj)为(6)式定义的个体xj的偏好距离。 根据(12)式,目标空间被划分为偏好区域和非偏好区域2部分。同时种群个体之间支配关系发生相应的改变,假设种群中任意个体xa和xb,当满足以下任意一条件时,定义xa偏好占优(Rd-dominance)xb。 1)xa和xb在同一个区域,xa在Pareto意义占优xb; 2)xa属于偏好区域,xb在非偏好区域。 算法通过g-占优结合偏好界限动态调整策略进化到一定代数后,得到具有一定偏好收敛特性的进化种群。后期为控制偏好解集范围,结合g-占优和偏好向量混合引导策略,同时增强候选解的选择压力。候选解之间混合偏好支配准则如下。 1)flagg值为1的个体支配其他分区内的个体,flagg值为1的个体之间采用Pareto非支配排序选择,相同Pareto非支配等级个体则采用Rd-dominance支配策略。 2)flagg为-1和0的个体均按Pareto非支配排序,同一Pareto支配等级个体按照Rd-dominance支配原则排序。 根据以上支配规则,混合偏好引导策略伪码如算法3所示。 算法3混合偏好引导种群个体支配选择策略 INPUT:合并种群P,种群规模N,决策点偏好点p(fp1,fp2,…,fpm),定义2个空档案集合Pflag=1和Pother,种群候选档案Palt, OUTPUT:Palt。 1.for eachxj∈P, do 2.if all(fiXj≤fPi) then 3.Pflag=1=Pflag=1∪{xj}//将位于偏好界限内的个体存储在Pflag=1中; 4.else 5.Pother=Pother∪{xj}//将在偏好界限外的个体存储在Pother中; 6.end if 7.end for 8.for eachxj∈P, do 9.根据(11)式计算Distance(xj); 10.end for 11.Xdirec=find(min(Distance(xj)) )//找出距离偏好点最近的个体; 12.ifNum(Pflag=1)≤Nthen//判断Pflag=1档案集中个体数量和N的大小关系; 13.Palt={Pflag=1}//将Pflag=1所有个体放入候选解档案集中; 14.num2=N-Num(Pflag=1) 15.对Pother非支配排序,得到个体支配等级frontvalue; 16.逐级选取个体放入Palt中,同一支配等级计算其偏好距离,选择不大于R的个体放入Palt中,若均在偏好区域内,根据拥挤距离排序选择,直到所选解个数为num2; 17.else 18.对Pflag=1非支配排序,得到个体支配等级frontvalue; 19.逐级选取个体放入Palt中,同一支配等级计算其偏好距离,选择不大于R的个体,放入Palt中,若都在偏好区域内,根据拥挤距离排序选择,直到所选解个数为N; 20.end if 21.P=Palt。 混合偏好引导个体支配关系示意图如图3所示。 图3 混合偏好引导个体支配关系示意图Fig.3 Diagram of individual dominance relationship guided by hybrid preference 种群内共有8个候选解,个体a4距离偏好点p最近,该个体和偏好点连线为偏好向量,根据混合偏好引导策略,此时的种群个体之间支配关系为a1=a2a3a4c1c2b1=b2;若采用g-占优策略,种群之间的支配关系为a1=a2=a3a4b2=b1c1=c2;若单独使用偏好向量,支配关系为a1=a2a3a4=c1c2b2=b1。对比发现采用本文所提混合支配策略能减轻候选解的选择压力,同时更能体现决策者的偏好。 本文所提两阶段混合引导偏好多目标优化算法(TSMg-NSGAII)流程图如图4所示,其中,it为算法迭代次数。 图4 算法流程图Fig.4 Algorithm flowchart 将本文所提算法和基于偏好点引导方式的g-NSGAII算法、基于偏好区域引导的r-NSGAII算法进行实验对比。根据文献[9],r-NSGAII算法设置各目标权重为平均权重,非支配阈值δ取值为0.1,为了对比分析,本文偏好向量引导的R也设置为0.1;为防止过度使用偏好区域调整策略,丢失种群多样性,本文所提算法中偏好收敛指标γ设置为0.5;前期基于偏好点的引导方式中设置it为20。在3种算法遗传操作算子设置上,选取模拟二进制交叉方法和多项式变异,设置相同的交叉概率和变异概率,分别取0.99和0.1。 实验选取ZDT[16]系列的ZDT1、ZDT2、ZDT3和DTLZ[17]系列中的DTLZ2作为基准测试函数。ZDT系列为两目标优化问题,种群规模N为100,最大迭代次数设置为200。对于DTLZ2测试函数,本文选取的是有三目标函数的DTLZ2,种群规模和最大迭代次数分别设置为150和300,同时为测试算法偏好点处于特殊位置的优化性能,根据偏好点和基准测试函数真实前沿位置关系,分别选取位于前沿上、不可行域和可行域这3种偏好点作对比试验分析,这些基准函数参数的设置和偏好点选取如表1所示。 表1 基准测试函数参数设置Tab.1 Parameter setting of test functions 本文选取世代距离(generational distance,GD)[18]指标来评价算法的收敛性能,定义为 (13) (13)式中,disi是种群中个体i到真实前沿的最小欧氏距离,此指标用来表示优化解集和真实前沿的接近程度,其值越小,表明该解集总体距离真实Pareto前沿越近,也即算法的收敛性能越好。 同时为评价算法的分布性能,采用SP指标[19],该指标能反映一个数据集的离散程度,用来衡量一定范围内临近解的差异大小,表征所得解集的分布性能,其数学表达式为 (14) 3.3.1 g-支配偏好区域界限调整策略优化性能分析 g-支配偏好区域界限调整策略根据算法迭代过程中种群个体分布情况,动态调整偏好区域界限,同时改变种群个体之间的偏好支配关系,增强g-支配的种群选择压力,偏好收敛性能得到提高。为测试该策略的有效性,该策略与对比算法g-NSGAII和r-NSGAII在ZDT1和ZDT2测试函数上得到的优化结果如图5所示。 从图5a可以看出,在ZDT1上且偏好点位于可行域时,g-NSGAII和r-NSGAII得到的解集均靠近偏好点(0.8,0.8)附近,但和真实前沿的距离没有本文算法近,即本文算法的前期收敛性更好。其中,基于r-占优策略的r-NSGAII算法所得到的偏好解集偏向于距离偏好点附近,因此,在算法前期进化种群会集中于偏好点附近。 图5b是偏好点位于ZDT2真实前沿上得到的结果,可以看出,g-NSGAII算法在可行域搜索,进化种群聚集于偏好点的一侧,而r-NSGAII算法所得解集在距离偏好点较近的目标空间区域搜索,本文算法采用动态调整偏好区域界限策略,所得到的解集收敛性更好,达到了算法前期得到具有一定偏好收敛性进化种群的目的。 图6为图5中对应的3种算法分别以ZDT1和ZDT2为测试函数,其种群迭代过程中的GD值变化曲线,可以看出,基于r-占优算法前期收敛速度较慢,且GD收敛曲线具有曲折性,算法收敛性能较差;本文算法得到的GD值最先达到最小值,并且始终优于其他2种对比算法,因此,收敛特性优于r-NSGAII和g-NSGAII算法。 图5 算法在ZDT1、ZDT2上迭代20代所得偏好解集Fig.5 Preferred solutions on ZDT1 and ZDT2 run by the algorithms for 20 iterations 图6 算法在ZDT1、ZDT2上迭代20代的GD进化曲线Fig.6 Evolutionary curve of GD on ZDT1 and ZDT2 run by the algorithms for 20 iterations 3.3.2 算法整体优化性能分析 3种算法在ZDT测试函数上运行所得的偏好解集如图7所示。图7a为偏好点位于ZDT1真实前沿上,运行3种对比算法所得的偏好解集,可以看出,g-NSGAII算法受此偏好点位置影响较大,解集收敛性较差;基于r-占优算法能得到收敛性很好的偏好解集,但偏好范围过于集中;而本文算法能得到收敛性能较好且满足决策者偏好范围的偏好解集。 图7b为偏好点位于ZDT1可行域时的优化结果,可以看出,r-占优所得偏好解集整体距离前沿最远,本文所提算法和g-占优算法所得偏好解收敛性能相当。但基于g-占优所得解集覆盖了整个真实前沿,不利于决策者的最终决策选择,而本文算法很好地控制了偏好解集规模,得到了满足决策者要求的部分非支配解。 图7c为偏好点位于ZDT2的不可行域得到的偏好解集,可以看出,本文算法和r-占优算法所得偏好解集收敛性相当,但本文算法得到的解集有着满足决策者偏好的偏好解集范围。而g-占优得到的偏好解集过多,不便于决策者决策。 图7d中测试函数为真实前沿非连续的ZDT3,且偏好点设置于其可行域得到的偏好解集,从图7d可以看出,g-NSGAII和r-NSGAII算法得到的偏好解集为局部偏好解,且r-占优所得解集的部分解没有收敛到真实前沿附近,而是收敛于偏好点附近。而本文算法得到的偏好解集收敛于真实前沿附近,收敛性优于g-占优,且很好地控制了解集的偏好范围,同时也表明本文算法能很好地解决具有不规则Pareto前沿的偏好优化问题。 图7 3种算法在ZDT测试函数上运行所得偏好解集Fig.7 Preferred solutions on ZDT run by the three algorithms 在三目标DTLZ2基准测试函数上运行3种算法所得的偏好解集如图8所示。图8a和图8b为偏好点位于其真实前沿面上得到的解集正面和侧面示意图。可以看出,随着目标维数的增多,g-NSGAII在此基准函数上所得偏好解集收敛性依旧很差; r-NSGAII和本文算法收敛性能相当,但解集分布过于集中,缺乏偏好多样性,不便于决策者最终决策;而本文算法得到了具有一定范围的偏好解集。 图8c和图8d为当偏好点位于非可行域时得到的优化结果的正侧面示意图。g-占优算法得到的解集不仅收敛性较差,偏好解集分布也过于分散; r-占优算法得到的结果收敛于前沿附近,但解集聚集在一起;本文算法得到的偏好解集收敛于真实前沿上,且分布在指定的偏好区域内。 另外,计算所得种群的GD指标和SP指标值,用来测试算法的收敛性能和分布性能。为了减少实验误差,每种算法基于每个偏好点独立运行20次,取其平均值作为指标最终计算结果。指标计算结果如表2和表3所示。加下划线的数值表示3种算法运行结果对比中的最小指标值,即该数值对应的算法在该测试函数上的优化性能最好。 通过表2和表3 可以看出,在几次试验结果中,GD值最小时对应的算法试验次数:g-NSGAI算法和r-NSGAII对应的都是2次最优,分别对应偏好点在ZDT1的不可行域和可行域、偏好点在ZDT2的可行域和在DTLZ2的不可行域的对比实验上。g-占优在ZDT1上表现最优的2次实验和本文算法得到的指标值相当,这是因为g-占优策略在解决简单二维优化问题,且偏好点位于非特殊目标空间位置上有着良好的收敛性能。r-占优在DTLZ2上表现最优的2次实验和本文算法所得指标值也相当,这是因为r-占优在解决三维优化问题上较g-占优收敛性能更好,且偏好点位于前沿上,能更快引导算法收敛到前沿区域。而本文算法的大多数实验结果最优,表明本文算法不受偏好点位置影响,并且针对不同Pareto前沿形状测试问题,都有着良好的偏好收敛性能。在表2中, 对应SP值最优的算法实验次数中,本文算法也占了大多数。因此,本文算法有着较好的收敛性和分布性能。 图8 3种算法在三目标DTLZ2 测试函数上运行所得偏好解集Fig.8 Preferred solutions on three-objectives DTLTZ2 run by the three algorithms 表2 3种算法在测试函数上分别运行20次GD计算结果 表3 3种算法在测试函数上运行20次SP计算结果Tab.3 Calculation results of SP obtained by running the three algorithms on test functions for 20 times 为分析本文算法收敛速度的情况,3种算法在测试函数上的GD进化曲线如图9所示。 图9a中,在有着非连续前沿的ZDT3上,当偏好点位于可行域时,算法前期本文加入动态偏好界限调整策略,GD指标优于g-占优策略,r-占优对此种优化问题较为敏感,前期收敛速度较慢,最终收敛性能稍差于本文算法。图9b中,偏好点位于DTLZ2前沿上,可以看出 r-占优在解决三维目标优化问题上能快速收敛。随着目标函数的增多,g-占优策略引导的种群中非支配解较多,选择压力增大,收敛速度较为缓慢。而本文算法前期收敛速度优于g-占优,后期收敛速度超过r-占优策略,最终收敛性能最优。 图9 3种算法在测试函数上的GD进化曲线Fig.9 GD evolution curve of three algorithms on test functions 本文提出了一种两阶段混合引导的偏好多目标优化算法,算法前期采用基于g-支配进化策略,结合偏好区域界限动态调整策略,进化到指定代数,获得偏好收敛性较好的候选种群,减少对不必要目标空间的搜索代价;后期结合决策者给出的偏好半径,采用偏好向量引导机制,控制偏好解集规模。通过对算法进行实验比较,结果表明,本文算法所得偏好解集不受偏好点具体位置影响,同时能控制偏好解集的规模,得到收敛性和分布性良好的偏好解集,便于决策者的最终决策。1.2 g-支配概念
1.3 快速非支配排序遗传算法

2 两阶段混合引导偏好多目标算法
2.1 偏好信息表示

2.2 动态调整偏好区域界限策略
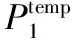

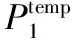




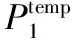
2.3 偏好向量引导策略
2.4 混合偏好引导策略

2.5 算法流程

3 实验分析
3.1 测试函数参数设置

3.2 性能评价指标

3.3 实验结果及分析







4 结 论

