双UAVs辅助的混合能量收集MEC系统资源分配策略

徐新雅，赵宜升，陶丽佳

(福州大学 物理与信息工程学院 福建省媒体信息智能处理与无线传输重点实验室，福州 350108)

0 引 言

移动边缘计算(mobile edge computing，MEC)技术[1]可以将用户计算任务卸载到边缘服务器，从而显著降低用户的计算压力。射频(radio frequency，RF)能量收集技术[2]是一种从周围环境电磁波中获取能量的新兴技术。将MEC与RF能量收集技术相结合，通过合理设计资源分配策略，不仅可以缓解用户计算压力，减少其能耗，还能高效利用收集到的能量。因此，研究结合MEC的能量收集通信系统中的资源分配问题，对提高系统性能具有重要意义。

结合MEC的能量收集通信系统的资源分配问题已经引起了广泛关注。文献[3]针对电子健康设备对低时延和实时监控需求的问题，引入雾计算技术，将任务卸载问题作为一个多阶段随机规划问题，通过对服务器计算能力、计算任务的大小以及任务是否卸载计算的决策进行联合优化，使系统总时延最小化；文献[4]研究了边缘计算系统中数据缓存和用户关联的问题，提出了一种智能数据缓存和动态用户关联的策略来最小化数据下载的时延；文献[5]在非正交频分多址辅助的MEC网络中，研究分流计算问题，在满足卸载速率、时延以及功率的约束下，实现卸载计算能量消耗最小化；文献[6]在双用户无线能量传输的MEC网络中，提出一种用户协作的思想，解决通信过程中的双远近问题，在满足数据卸载速率与电池容量的约束下，通过优化时间资源分配来最大化用户最小能量效率；文献[7]在异构物联网的分布式能量收集MEC系统中，针对边缘云的计算资源如何按需分配的问题，提出一种基于博弈论和扰动李雅普诺夫优化理论的在线分布式优化算法来联合优化任务卸载决策、计算资源分配和电池能量管理；文献[8]在具有RF能量收集和MEC功能的异构无线网络中，针对用户能量受限问题，提出多频段能量收集并将任务分流到边缘服务器计算的方案，在用户能耗、总的数据传输速率、子载波分配以及功率的约束下，实现能量效率最大化；文献[9]为提高移动设备服务质量，引入无人机(unmanned aerial vehicle，UAV)作为移动的MEC服务器分担用户计算任务，通过联合优化移动设备计算资源、功率消耗以及UAV天线的半功率波束宽度，使总的功率消耗最小；文献[10]在物联网非正交多址上行传输系统中，提出一种UAV作为移动基站为物联网设备提供可靠通信的方案，通过联合优化子信道分配、物联网节点上行发射功率以及UAV高度，最大化系统容量。然而，现有的研究主要集中在RF能量收集方面，由于基于RF能量收集的接收功率较低，短时间内收集到的能量较少，当电池能量耗尽时，系统性能将会受到严重影响；文献[11]研究了基于太阳能供电的UAV通信系统资源分配问题，设计了一种在线资源分配策略，通过联合考虑UAV飞行轨迹、发射功率及子载波分配，在给定时间周期内最大化系统吞吐量。本文受文献[8]中多频段能量收集和文献[11]中太阳能收集的启发，如果将多频段RF能量收集与太阳能收集相结合，让UAV在高空时收集太阳能，在低空时收集RF能量，就可以获取充足的能量。同时，将UAV作为移动专用RF源为用户近距离充电，可以在一定程度上减少RF能量传输损耗，且用户能够收集足够的能量，从而保障系统性能。

针对用户能量受限问题，本文提出一种UAVs协助的混合能量收集边缘计算系统总能耗最小化的资源分配策略。本文的主要贡献总结如下。

1)针对用户能量受限且计算资源有限的问题，引入2个具有混合太阳能和RF能量收集功能的UAVs。一个UAV携带MEC服务器，当用户计算任务较大时，可将任务卸载到该UAV以减少自能耗。另一个UAV作为专用RF源，能够飞到能量不足的用户上方，为其补充能量。

2)联合考虑2种UAVs和用户的能量消耗，将系统资源分配问题建模为混合整数非线性规划(mixed-integer nonlinear programming，MINLP)问题。以最小化系统总能耗为目标，同时满足UAVs和用户最大计算能力及能量消耗的约束。

3)针对建模的MINLP问题，为了降低求解复杂度，通过引入量子行为粒子群优化(quantum-behaved particle swarm optimization，QPSO)算法获得次优解，并通过仿真对提出的资源分配策略进行性能评估。

1 系统模型

本节研究系统模型，给出了UAVs协助的能量收集MEC系统网络结构，并分析UAVs和用户能量收集与消耗模型。

1.1 网络结构

双UAVs辅助的混合太阳能与RF能量收集MEC系统网络结构如图1所示。网络中存在2个UAVs和K个用户。UAVRF利用收集的太阳能和RF能量为用户充电。采用ak∈{0,1}表示UAVRF是否需要为用户传输能量的判断，其中，ak=1代表UAVRF需要为用户传输能量，否则ak=0。UAVMEC携带边缘服务器，用户k(k=1,2,…,K)可将计算任务卸载到UAVMEC计算。采用bk∈{0,1}表示计算任务是否卸载计算的决策，当bk=0时，计算任务通过本地计算来完成，否则，bk=1。采用Tk=(Dk,Ck)表示用户k的计算任务。其中，Dk表示需要计算的数据量，Ck表示完成Dk所需要的CPU周期数。

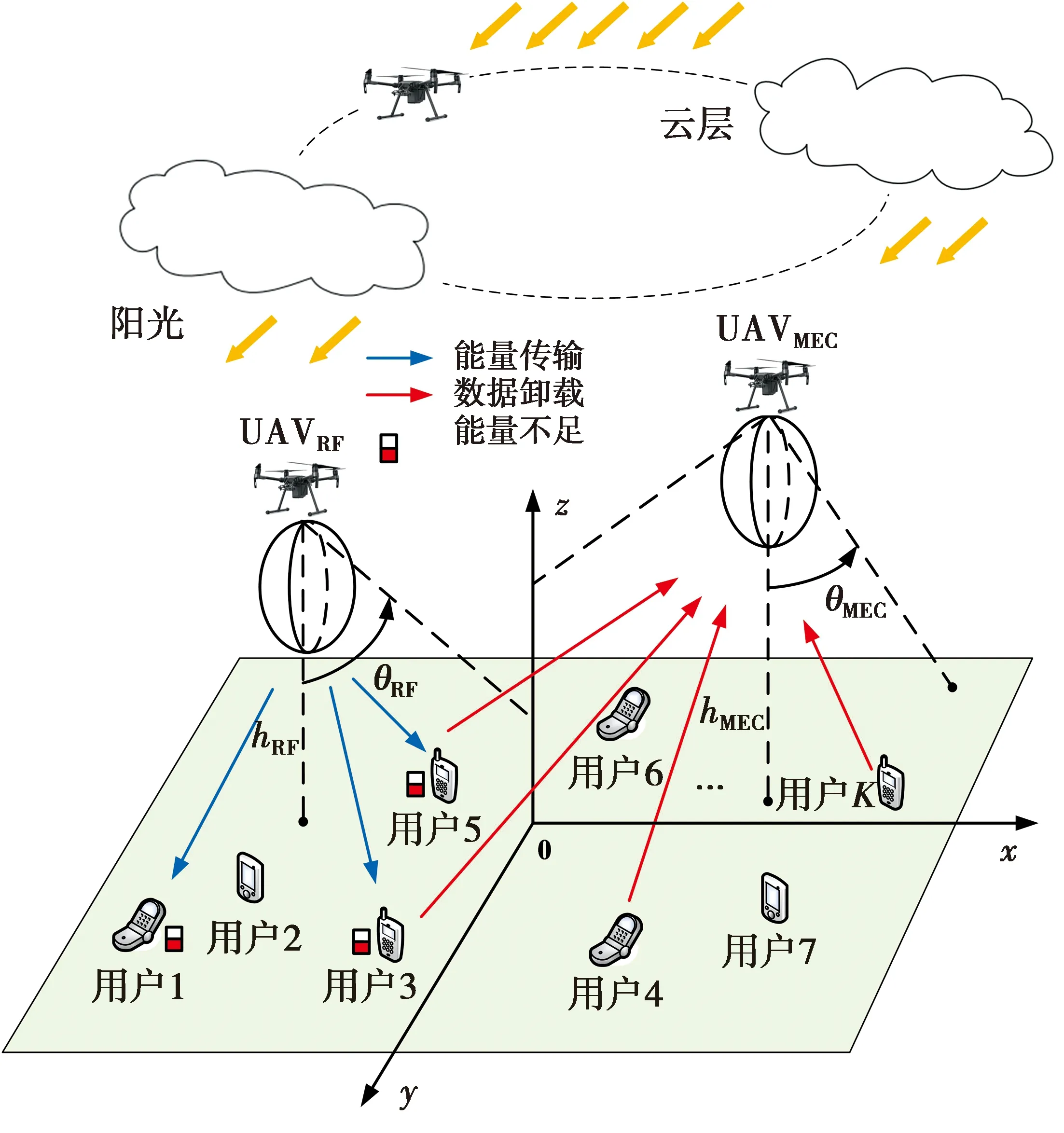
图1 双UAVs辅助的混合能量收集MEC网络场景Fig.1 Communication scenario of dual UAVs-assisted MEC system with hybrid energy harvesting

1.2 UAVs和用户能量收集模型

本节分析UAVs和用户能量收集模型。UAVs和用户随机分布在一个以米为单位的三维直角坐标系中，假设UAVRF位置为(xURF,yURF,hURF)，UAVMEC位置为(xUMEC,yUMEC,hUMEC)，他们可以从太阳光中获取能量。由于太阳光线穿过云层时存在衰减，根据文献[12]，其衰减量可以表示为

ψ(dcould)=e-αdcould

(1)

(1)式中：α为云层吸收太阳光的系数；dcould为太阳光穿过云层的距离。因此，UAVRF在高度hURF处的太阳能输出功率为[11]

(2)

此外，电视塔(TV tower)和基站(base station，BS)作为环境RF源为UAVs和用户提供能量补充。假设第i(i=1,2,…,I)个RF源的位置为(xi,yi,0)。根据Friis公式[10]，UAVRF的RF能量接收功率可以表示为

(3)

(4)

(5)

对于用户的能量收集模型分析如下。假设用户的坐标为(xk,yk,0)。根据文献[13]，用户k在tkR时间段从环境电磁波中收集的能量为

(6)

(6)式中：GkR为用户k接收天线增益；ηkR为能量转换效率；di,k为RF源到用户k的距离。

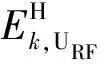
(7)

(8)

为确保用户可以从UAVRF获取能量，并且能够将数据卸载到UAVMEC，用户k到UAVs的水平距离需要满足dk,URF≤hURFtanθURF和dk,UMEC≤hUMECtanθUMEC的约束，其中，2θURF和2θUMEC分别表示UAVRF与UAVMEC定向天线半功率波束宽度，本文取值2θURF=2θUMEC=π/2 rad[14]。

2 问题建模和求解

本节提出具体的资源分配策略。建立资源分配优化问题的模型，然后引入QPSO算法获得次优解。

2.1 问题建模

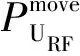
(9)

(10)

(11)

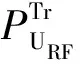
(12)

(13)

(13)式中：κ是一个与用户CPU类型有关的常数。

由于用户计算资源有限，UAVMEC可以辅助用户完成任务。根据香农定理[15]，Tk上行传输速率为

(14)

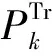
(15)

采用β表示UAVMEC计算每比特数所需的CPU周期数；ε为每CPU消耗的能量。因此，UAVMEC执行任务Tk所消耗的能量可以表示为

(16)

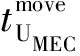
(17)

(18)

资源分配问题的优化目标是最小化系统总能耗，同时满足若干约束条件。因此，该问题可以建模为

(19)

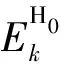
2.2 算法求解

对于建模出的MINLP问题，可采用复杂度适中的启发式算法求其次优解。粒子群优化(particle swarm optimization，PSO)算法[16]是启发式算法的一种。它是从生物种群行为特性中得到启发并用于求解优化问题的一种方法。在PSO算法中，粒子的运动轨迹由其速度与位置决定。第n(n=1,2,…,N)个粒子在第q次迭代时的速度和位置分别为

(20)

(20)式中：Vn表示第n个粒子的速度；Pn代表第n个粒子的局部最优位置；G为粒子群的全局最优位置；w为惯性因子；c1和c2为加速度常数；r1和r2是位于(0,1)随机分布的常数。在PSO算法中，粒子是沿着一个确定的轨迹在牛顿力学空间里运动的，这会导致其位置变化缺少随机性，易陷入局部最优的陷阱。针对PSO算法的缺点，孙俊等将量子行为引入到PSO算法中，提出了QPSO算法[17]，在QPSO算法中，粒子的状态不再由其位置和速度决定，而是通过一个波函数来确定，与PSO算法相比，QPSO算法随机性更强，粒子群体智能程度更高，能够克服PSO算法早熟收敛的不足。因此，采用QPSO算法求解(19)式所述的MINLP问题。具体的求解流程如图2所示。

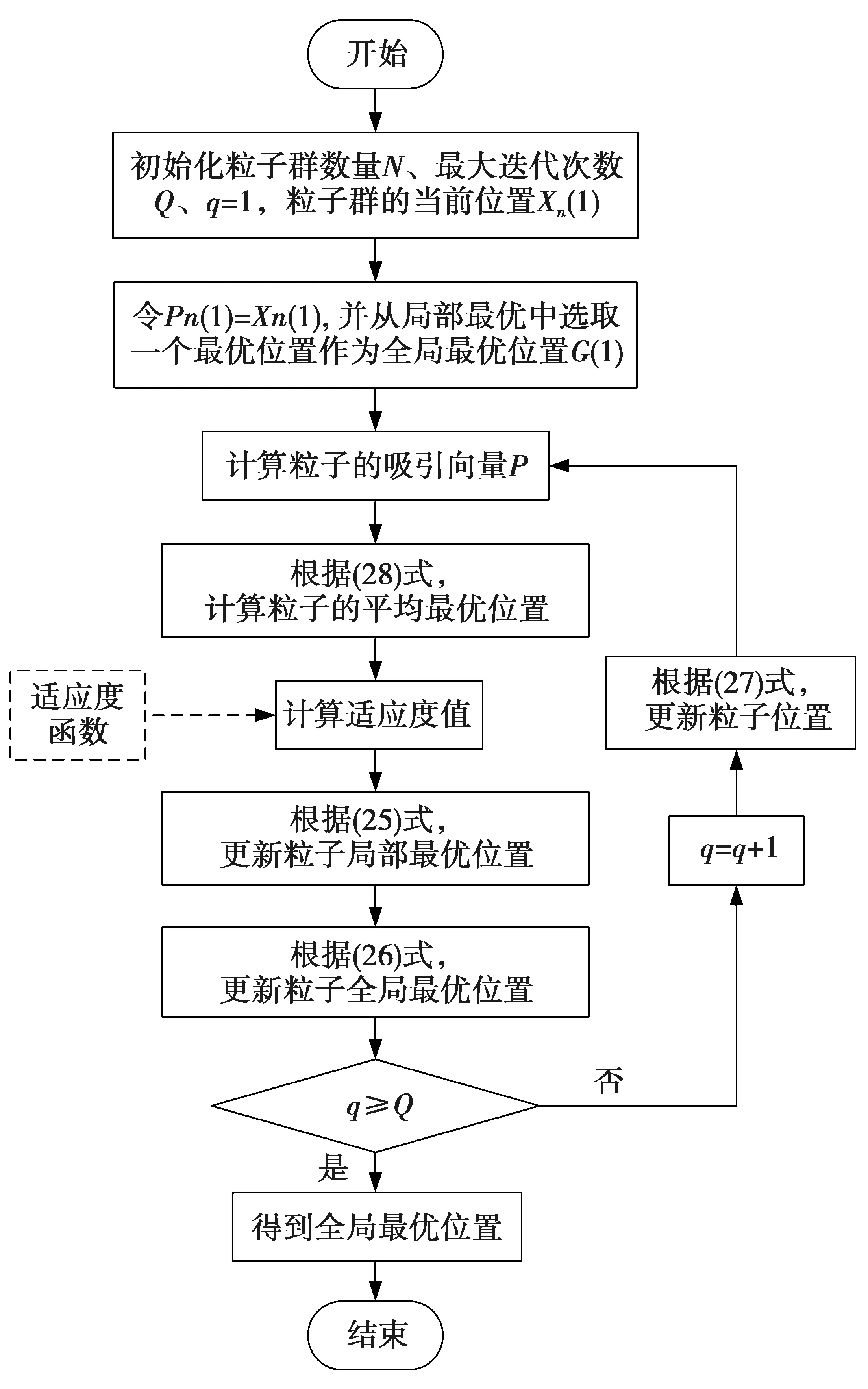
图2 基于QPSO算法的资源分配优化流程图Fig.2 Flow chart of resource allocation optimization based on QPSO algorithm

首先，通过构造一个适应度函数，将受约束的问题转换成无约束的形式，该函数由目标函数和惩罚函数组成，具体形式为

(21)

(22)

对应问题(19)中的7个约束条件，具体形式表示为

(23)

(23)式中：max(·,·)表示在2个数值中取较大的一个。

然后，对粒子进行定义。在多维的目标搜索空间中，QPSO算法是由N个代表潜在问题解的粒子组成的群体，第n个粒子的位置矢量可以表示为

(24)

对于所建模的最小化问题，目标函数值越小，相应的适应值越好。因此，第n个粒子的局部最优位置由(25)式决定。

(25)

同理，粒子群的全局最优位置由 (26) 式决定。

(26)

为保证算法收敛，需要定义吸引子矢量P，P=φPn(q)+(1-φ)G(q)，由粒子的局部最优位置和全局最优位置共同决定，其中，φ是位于(0,1)的随机数。此外，第n个粒子的位置更新方程为

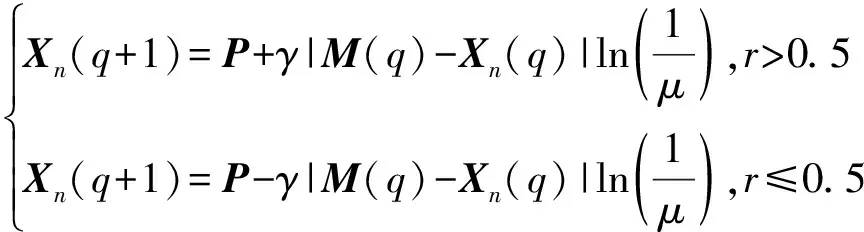
(27)

(27)式中：μ与r是位于(0,1)的随机数；γ=1-q/2Q为控制参数；M(q)表示每个粒子局部搜索最优置的平均值，其表达式为

(28)

3 性能评估

本节通过仿真对所提出的资源分配策略进行性能分析，给出相关参数设置并分析其性能。

3.1 参数设置

3.2 性能分析

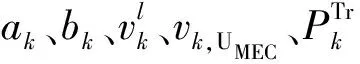
表1给出了10个不同的用户分别从不同的RF源收集能量的情况。通过对表1的分析可知，用户从UAVRF中收集的能量最多，其次是TV tower1和TV tower2，从BS1和BS2中收集的能量较少。这是因为TV tower1、TV tower2的传输功率比UAVRF大，但距离用户远，RF能量传输时空间损耗大，所以用户接收到的功率较小。而BS1、BS2相对于UAVRF，不仅距离用户远且传输功率小，因此，用户从BS1、BS2收集到的能量较少。

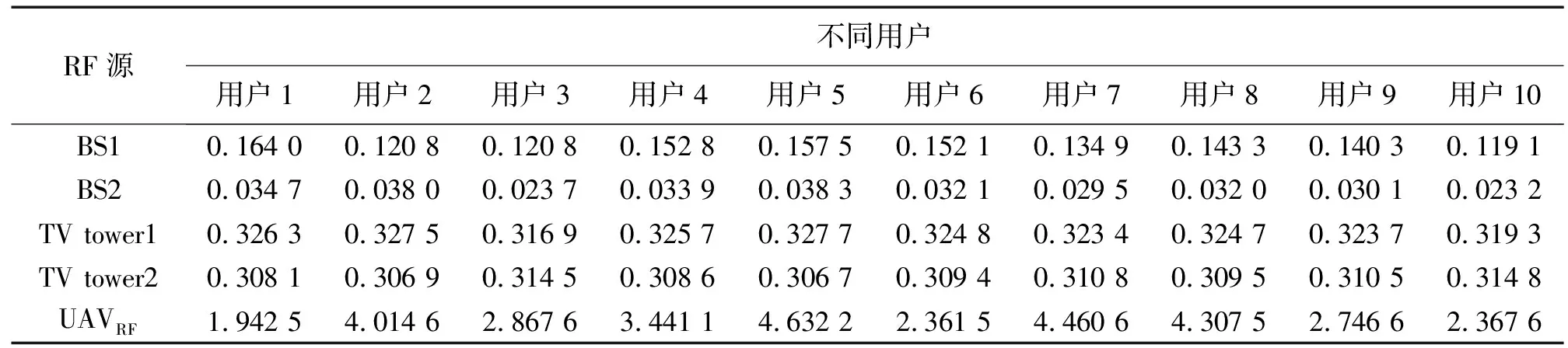
表1 不同用户从多个RF源收集的能量Tab.1 Energy harvested by mobile devices from different RF sources J

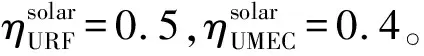
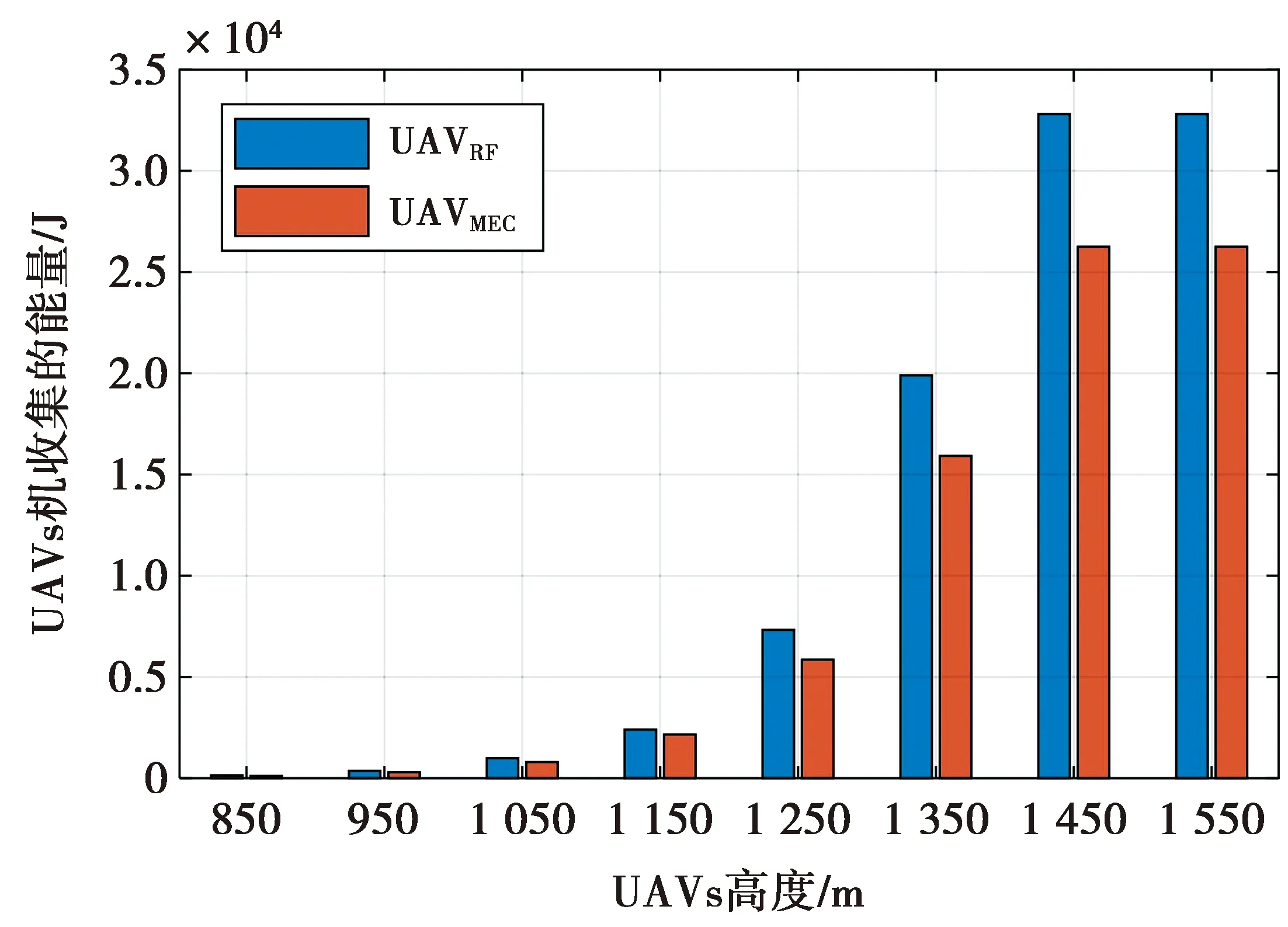
图3 UAVs收集的能量与其高度的关系Fig.3 Energy harvested by unmanned aerial vehicle versus altitudes

图4对比了在不同粒子数目下，采用QPSO算法求解时，迭代次数对系统总能耗的影响。在仿真中，用户的数量k=16。从图4可以看出，系统总能耗随迭代次数的增加而减少，当迭代次数为120时，总的能耗趋于稳定。此外，随着粒子数从8逐渐增加到45的过程中，系统总能耗也逐渐减小。这是因为从更多的粒子数中搜索得到的结果将更接近最优解。

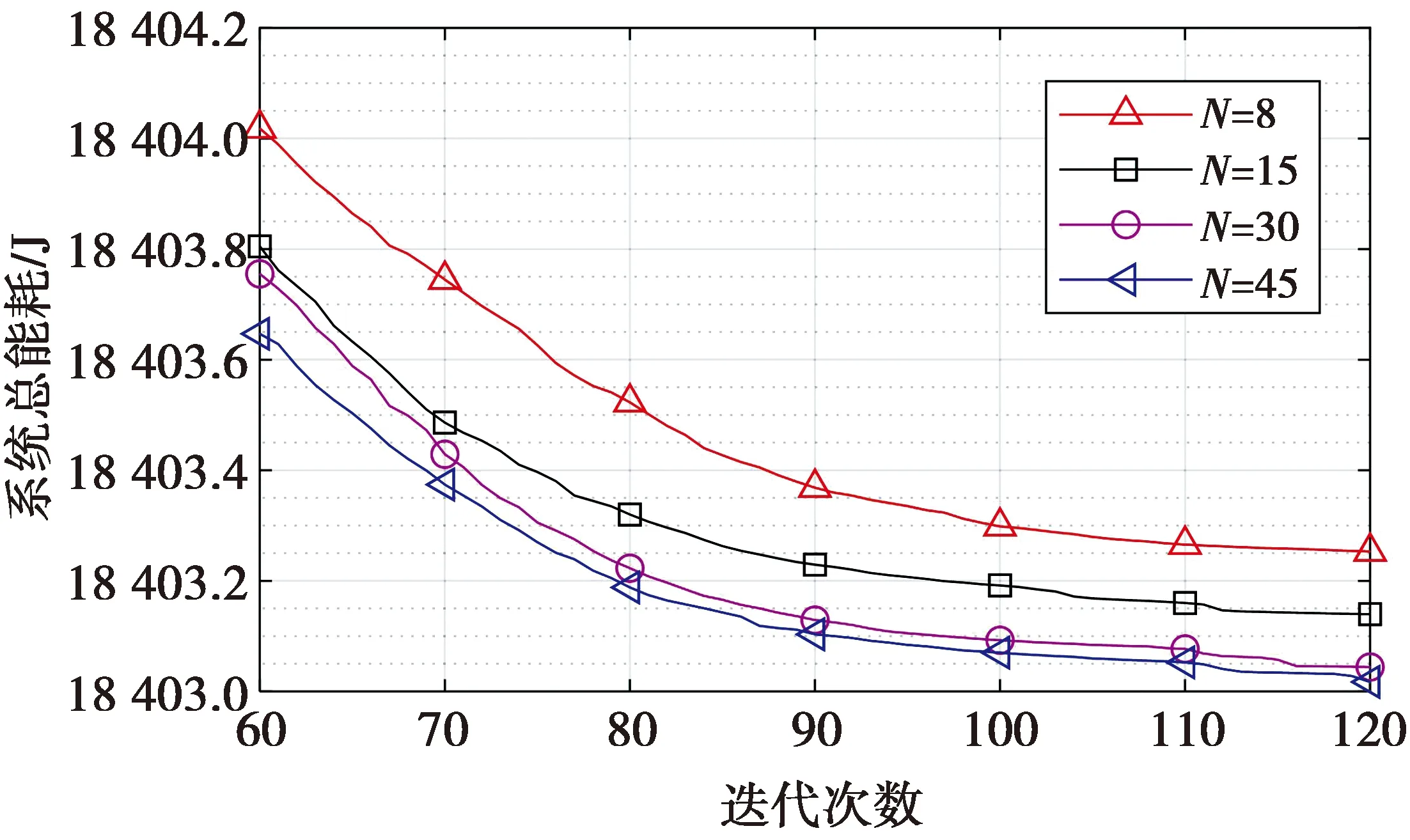
图4 系统总能耗与迭代次数的关系Fig.4 Total energy consumption versus number of iterations

图5从平均CPU时间的角度对比了在不同粒子数目下QPSO算法的时间复杂度与迭代次数的关系。从图5可以发现，随着迭代次数的增加，平均CPU时间呈现逐渐上升趋势，而且粒子数目越多，平均CPU时间越长。这是因为问题的求解是通过粒子位置进化方程的迭代更新来实现的。在多维解空间中，每个粒子的位置为多维矢量。因此，粒子数目越多，通过迭代更新得到粒子全局次优解所耗费的时间就越长。

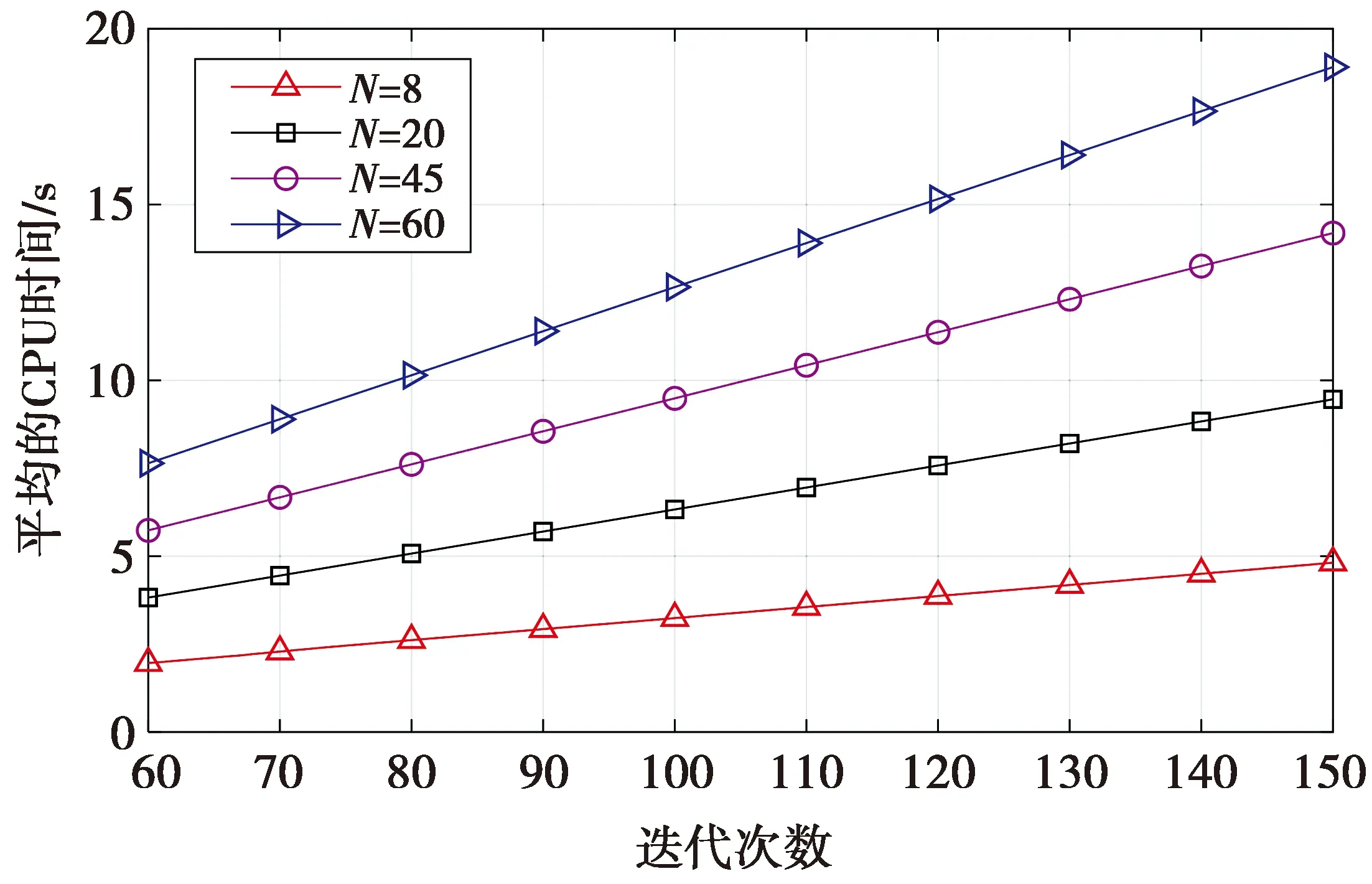
图5 平均CPU时间与迭代次数的关系Fig.5 Average CPU time versus number of iterations

图6对比了不同方案下，系统总能耗与用户数量的关系。从图6可以看出，随着用户数量的增多，系统总能耗也随之增加。一方面是因为每个用户执行任务时会消耗一定的能量，用户数量的增加必然会引起所有用户总能耗上升；另一方面是因为随着用户数量的增多，UAVs将会耗费更多的能量为用户提供服务。此外，由于PSO算法在求解过程中，只能得到局部次优解，所以采用QPSO和FCR-QPSO方案得到的系统总能耗比PSO与FCR-PSO方案少。从图6还可以看出，与FCR-QPSO方案相比，QPSO方案消耗的能量更少，这是因为在QPSO方案中，通过QPSO算法对所有自变量都进行了优化，而在FCR-QPSO方案中UAVMEC分配给用户的计算资源是固定的，因此，QPSO方案的优化效果更好。

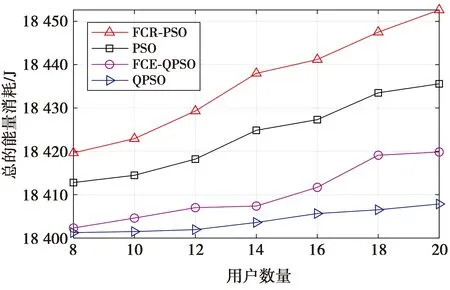
图6 总的能量消耗与用户数量的关系Fig.6 Total energy consumption versus number of users

4 结 论

针对用户从环境RF源收集能量较少的问题，提出了一种UAVs辅助的混合太阳能和RF能量收集MEC系统中最小化系统总能耗的资源分配策略。通过部署2个具有混合能量收集功能的UAVs，分别为用户提供边缘计算服务和补充能量。当用户的计算任务较大时，可以将计算任务分流到UAV携带的边缘服务器进行计算。当用户从环境RF源收集的能量不够用时，另一个UAV为其近距离补充能量。在保证用户和UAV计算能力和能量消耗的前提下，以最小化UAVs与用户的总能量消耗为目标，采用QPSO算法获得次优解。仿真结果表明，提出的算法效果更好。本文在考虑UAV为用户补充能量时，忽略了轨迹优化，在未来的工作中，将进一步研究UAV为多个用户补充能量时的轨迹优化问题。