深入探究基本图形 渐次展开一题一课—— 以“相似三角形的判定”单元复习课为例

⦿广东省深圳科学高中龙岗分校 洪顺庆

⦿浙江省杭州市余杭区海辰中学 程龙军

1 引言

单元复习的主要功能是回顾知识和解决问题.传统复习方式习惯于知识梳理、例题讲评、巩固训练式的流程，导致课堂存在“大容量、小问题，浅思考”的现象，学生对数学问题浅尝辄止.为此，笔者提出“一题一课”的单元复习形式，通过对问题的不断分析、不断联系、不断深入，引发学生思考，激发学生讨论，提供更多的机会让学生发现和提出问题，分析和解决问题，培养学生整体性、系统性、综合性的思维方式，从而让深度学习真正发生.下面以沪科版九年级上册“22.2 相似形的判定”单元复习为例，探讨一题一课式单元复习教学设计.

2 内容解析

本单元是沪科版数学教材九年级上册第22章的第二单元，在全等三角形和比例线段的相关知识基础上，研究相似三角形的预备定理和四个判定定理.这些内容为发展学生的几何直观和逻辑推理能力提供了重要素材，也为后续学习圆和三角函数的内容奠定了基础.与全等三角形相比，本单元基本图形众多，基于比例式的逻辑推理较为抽象，学生在之前的新授课学习中，还不能深刻理解和应用基本图形，也不能熟练运用比例式进行变形和推理.因此，单元复习课中亟需加强对判定定理的理解与应用，构建各知识点和基本图形之间的关联，形成知识结构.基于上述考虑，特制定了如下教学目标：

(1)理解相似三角形中基本图形的相互关系；

(2)会利用相似三角形的判定解决一些问题；

(3)经历基本图形逻辑关系的探索过程，体验解决问题策略的多样性.

3 教学过程

3.1 温故知新

问题1相似三角形的判定有哪些？类比全等三角形，说说两类判定之间的联系.

教学说明：学生逐条梳理相似三角形的判定，得到几个判定之间的结构关系(如图1)，然后类比全等三角形，说明全等和相似之间特殊与一般的关系.复习课一方面要了解学生对知识的掌握情况，使复习更有针对性；另一方面也要体现单元知识的结构，这也是它功能和价值的体现，表现在已经了解几何知识学习流程的基础上，明确研究思路和研究方法，形成框架性的总结，为后续的灵活运用做准备.

图1

3.2 合作探究

问题2如图2，在△ABC中，已知点D，E分别为边AB，AC上的一点，请补充一个合适的条件，使△ABC与△ADE相似.

图2

教学说明：在学生原有的知识经验中，平行或斜交原三角形可以得到“A型相似”和“反A型相似”，这是解本题的依据和突破口，其中图形的运动变化过程也是复习课要关注的.借助图形和相似三角形的判定，从角和边两个角度自主探究，可能的结论如下.

图3

图4

本题设置了一个入口宽且解法多样的开放性问题，有效整合了学生知识结构中的零散知识.学生既可以从角又可以从边的角度去补充条件.较问题1，问题2体现出将学生的认知从识记提升到理解和应用的层次，并迅速吸引了学生眼球，激发学生的探究欲望.

问题3如图5，当∠1=∠ACB时，连接BE,CD交于点F，试猜想图中有几对相似三角形，并证明你的猜想.

图5

教学说明：学生分组讨论并猜想图中的相似三角形，可能的答案有①△ADE∽△ACB,②△ABE∽△ACD,③△FDB∽△FEC,④△FDE∽△FBC，等等.教师引导学生明确思路，依次证明①②③④.本题的难点有两个，一是由△ADE∽△ACB推导出△ABE∽△ACD，二是由△FDB∽△FEC推导出△FDE∽△FBC.教师需要引导学生细致分析比例式并根据需要适当变形，寻找已知条件和目标的差异.学生也有可能会猜想△EFD与△EDB相似，对于这个假命题，可引导学生用分析法进行推理.假若△EFD∽△EDB，则∠EDF=∠EBD.由∠ECD=∠EBD，可得∠ECD=∠EDC，则有ED=EC.因为DE可以平行移动，因此ED=EC未必成立.故△EFD与△EDB不一定相似.

问题4如果把问题3中的条件∠1=∠ACB换成∠ECD=∠EBD，上述四对三角形还能相似吗？

教学说明：本题是问题3的一个变式，通过上题的探究，学生意识到只需证明①②即可，而③④无需重新证明.通过此题强化了相似三角形判定的综合运用，并由此得出“如果上述四对三角形有一对相似，则其余的三对也相似”.其实，例题的选择不一定要多，有时只需对原有问题适当变式拓展或综合利用，就能形成图形的生长、知识的生长和思维的生长，达到举一反三的效果.

问题5如图6，当∠1=∠ABC时，连接BE，CD交于点F，图中有几对相似三角形？

图6

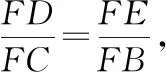
问题3与问题5的图形都是从一个母题特殊化得来，图形结构类似，前者对后者产生较强的负迁移，学生习惯性地认为前面的四个结论也成立，加之问题5是开放性问题，这更增加了问题的难度.学生对于常见真命题的证明容易上手，而本题是需要证伪.这个证伪的挑战性任务引导学生经历了类比和思辨的过程，培养了学生推理的严密性，发展了学生评价和质疑的能力.

问题6如图7，当∠1=∠ABC时，连接BE,CD相交于点F，连接AF并延长交BC于点O，交DE于点M.

图7

求证：OB=OC.

3.3 总结回顾

问题7结合图8，说说本节课你应用了哪些知识？有哪些收获和困惑？

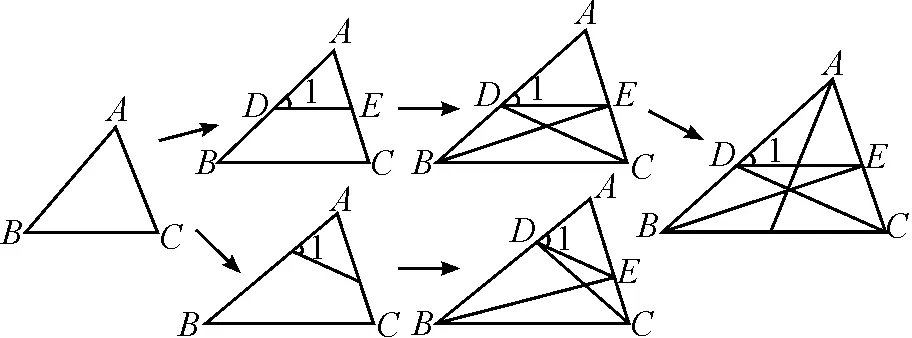
图8

教学说明：通过上述图形的不断特殊化，引导学生对基本图形进行结构化处理，建立易于理解和迁移的图式，同时将相似三角形的判定等知识点串联在其中，有效提高了课堂效率，使得复习课同时具备了总结、应用和探究的功能，调动了学生的学习积极性，发展了学生的高阶思维能力.

4 教学思考

4.1 一题一课，提升课堂教学效率

本节单元复习课区别于概念加例题的常规复习形式，采用了一题一课、一图一课的形式，这种形式简洁高效，兼顾了知识回顾和解决问题这两个复习课的重点，节省了读题审题的时间，减轻了学生课堂学习负担，提高了探究意识和学习兴趣；同时，探究过程兼顾不同学生的学习需求，使得不同的学生在一节课里可以得到不同的收获.对于一题一课的设计，首先要选取一个好的母题，其来源可以是教材中的例题与习题，也可以是从中提炼出的基本图形.母题需要与单元知识点密切相关，并能够提供足够的探究空间，使问题可以不断生长，进而在解决问题过程中将单元知识点有序串联.

4.2 问题驱动，引领学生深度学习

本节课从一个基本图形入手，回顾相似三角形的判定定理，之后题设条件渐次增加，在不断变化的问题情境中，精心建构开放性问题，一步步特殊化基本图形，结合变式和拓展，形成了由易到难的问题串.这样的问题设计，知识的运用与生成是自然的，又是有迹可循的，学生容易理解.随着问题的不断推进，学生对知识点反复提取和加工，在综合运用单元知识和思想方法解决挑战性问题的过程中，经历了应用、质疑、反思、评价等多层次的高阶思维，其思维层级逐渐提高，理解程度逐渐加深，学生在体验中深刻理解了相似三角形的判定定理，也增强了正确运用判定定理的自觉性.

4.3 多维一体，推动数学知识结构化

数学复习课的目标是回顾知识、训练思维、发展能力.本节课从知识的联系出发，把新课中分几个课时研究的内容完整地放到一个单元复习课中，具有结构性、系统性、逻辑性，有助于构建思维导图.在温故知新环节，依据知识的逻辑关系把零散的知识点构建成脉络结构，学生可以系统了解知识的发生发展过程，进而理解单元知识，形成整体架构.在合作探究环节，通过循序渐进的问题串，既回顾了单元知识点，又挖掘了其中蕴含的数学思想方法和解题策略，如分类思想、转化思想，逆推法、正难则反的策略等，这正是优化认知结构的关键.在总结回顾环节，学生明确了本单元中一般图形与特殊图形的关系，形成了知识结构图示，方便在使用时快速提取.从结构化思维的角度来说，单个知识点的复习是必要的，但更要注重知识之间的结构生成和数学思想方法的提炼，包括各个图形的演变及其相互的联系，学生在经历整理、练习、对比、辨析的过程中，可以更好地对数学知识进行再认识和结构化的学习.