多关联 勤思考 促提高

⦿苏州工业园区星湖学校 沈 奕

1 原题展示

(2021江苏泰州15题)如图1，在平面直角坐标系中,点A坐标为(8，5)，⊙A与x轴相切，点P在y轴正半轴上，PB与⊙A相切于点B，若∠APB=30°，则点P的坐标为______.

图1

2 试题评价

2.1 简而不凡，内涵丰富

本题以圆、切线、30°角、点的坐标等常见素材为背景设置问题，图形简约而熟悉，题干精炼而别致，结构简单而富有美感，是一道内涵丰富、设计巧妙、考查学生素养的填空题.

从背景条件来看，涉及知识点丰富，有点的坐标、切线的判定与性质、特殊四边形的判定与性质、相似、勾股定理等核心知识.

从转化策略来看，蕴含多个基本图形的构造，如：添平行线构造“8字形”“A字形”证三角形相似，连接圆心与切点，将点的坐标转化为垂线段的长度，见直角构造“一线三垂直”.将几何问题转化为代数问题(方程)，通过逻辑推理与数学计算进行解答.

2.2 突出能力与基本素养

求点的坐标的实质是求出线段长，求线段长是初中几何最为常见的一种题型，同时也是高中生必备的解题基本功之一.其解题思路是：(1)将待求线段放到全等图形中，运用全等三角形的性质求出线段长；(2)将待求线段放在特殊图形(如平行四边形、直角三角形)中，并运用这些图形的特殊性质进行推理或运用线段和差进行综合分析求解；(3)将待求线段放在相似三角形中，运用题目条件或构造“8字形”“A字形”或其他基本结构，运用相似性质推理；(4)其他的还有勾股定理，锐角三角函数，平移、旋转、轴对称等几何变换等.

本题求线段长的方法灵活多变，既考查学生的基本数学知识、数学思想、数学技能及数学基本经验，又考查学生对数学本质的理解.同时本题需添加辅助线才能解决，对模型意识、逻辑推理、数学运算、图形直观、图形分析等考查到位.

2.3 方法多样，考查探究意识

数学教学的核心是如何培养学生的理性思考能力，盲目的堆砌式解题方法，不仅不会促进学生思维能力的发展、技能的形成，相反会使学生厌恶数学.如何激发学生的理性思维?一题多解无疑是一种有效的方法.对于本题，可以从内部知识的关联性，以“在哪里？那里有什么？要到哪里去”为思考问题的路径，发散思维，多联系、多角度深入思考，便可以得到不同的解法，从而有效发展学生的创新精神与探究意识，更重要的是让学生的理性思维得以拓展，不受惯性思维模式的束缚，培养思维品质和应变能力.

3 题意分析及解答

在解答之前应该意识到，点A的坐标(8，5)及30°角是我们要牢牢把握和突破的思维核心.一般来说见30°角想到含30°角的直角三角形，因此，只需连接圆心与切点就可以办到.所以连接圆心与两个切点(设圆与x轴相切的切点为点C)，由切线的性质得OC=8，BA=CA=5.但PB是斜线段，无法与坐标有效联系起来.因此还要分析题目中的其他隐含信息，作出其他辅助线.

思路一：构造特殊四边形.

分析：点A坐标为(8，5)，在图2中已经用水平线段或竖直的垂线段表示出来.在Rt△PAB中，∠APB=30°，BA=5，则PA=10.如果不作辅助线，解题思路受阻.因此，下一步的解题重点是如何作出辅助线，有效运用已知条件.

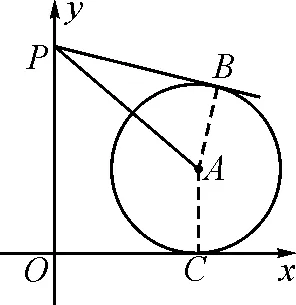
图2

此时，我们可以将解题目标转向题目所求：“求点P的坐标”，要求出点P的坐标，必须出现水平线段或竖直的垂线段.实现解题目标有下列三种方法：

(1)过点P和点A作水平线及垂线，构造矩形，利用矩形性质及勾股定理；

(2)过点A作y轴的垂线，构造矩形，利用矩形性质及勾股定理；

(3)过点C作PA的平行线，证明平行四边形和直角三角形.

方法一：以P为直角顶点构造长方形.

解：连接CA并延长，过点P作PH⊥CA，交CA的延长线于点H，如图3所示，则四边形PHCO为长方形.

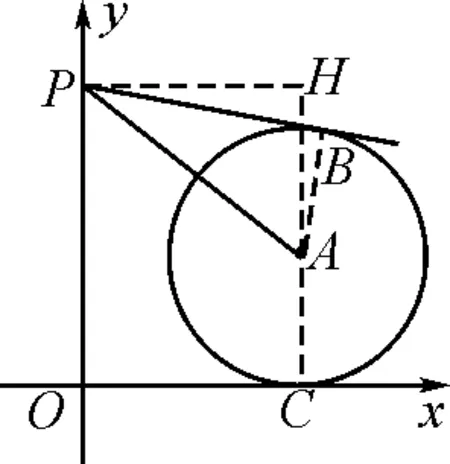
图3

由切线的性质得∠PBA=90°，而∠APB=30°，所以在Rt△APB中，PA=2AB=10.

又矩形PHCO的边CO=8，所以PH=8.

Rt△PAH中，由勾股定理得

因此PO=HC=HA+AC=6+5=11.

故点P的坐标为(0，11).

方法二：以A为直角顶点构造长方形.

解：连接CA，BA，过点A作AH⊥PO，垂足为H，如图4所示.

图4

由三个直角知四边形HACO为长方形.

由点A坐标为(8，5)，所以AH=8.

由切线的性质得∠PBA=90°，而∠APB=30°，所以在Rt△APB中，

PA=2AB=10.

所以PO=PH+HO=6+5=11.

故点P的坐标为(0，11).

方法三：构造平行四边形.

解：连接CA，BA，过点C作PA的平行线CN，交PO于点N,如图5所示.

图5

由AP∥CN，PN∥AC，得四边形PNCA为平行四边形.

所以PN=AC=5，NC=PA=10.

所以PO=PN+NO=5+6=11.

故点P的坐标为(0，11).

点评：在平面直角坐标系中求点的坐标，一般的解题策略是作坐标轴的平行线，出现水平线段或竖直的垂线段，将代数问题转化为几何推理.而特殊四边形的内涵丰富，性质繁多，可以有效实现这一目标.

思路二：构造“ 一线三垂直”相似.

分析：题目的原图与课本的“切线长定理”有一定关联.原图已经有一条切线，可以过点P作圆的另一条切线，并利用平面直角坐标系的垂直结构构造“一线三垂直”基本图形，证明直角三角形相似.

方法四：作切线，构造“一线三垂直”相似.

解：连接CA，BA，过点P作⊙O的切线PE，切点为E，连接AE，过点E作OC的平行线交PO于点G，交AC于点F.如图6所示.

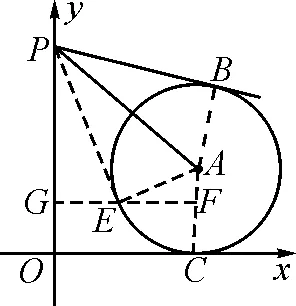
图6

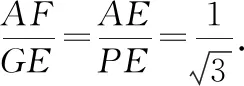
故点P的坐标为(0，11).

分析：由前面分析知∠PBA=90°，结合所求的目标是点的坐标，需出现直角或水平线，再类比“方法四”，可以以点B为直角顶点构造“一线三垂直” 基本图形，证明直角三角形相似.

方法五：作水平线，构造“一线三垂直”相似.

图7

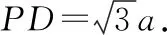
在Rt△ABH中，由AH2+BH2=AB2，可得

故点P的坐标为(0，11).

点评：联系课本中的基本定理，基本图形，结合已知条件中的切线，再结合题目所求，需出现水平线与垂线段，三者发力，并加以联系，将数学问题转化为几何基本模型，再运用几何图形的性质，进一步转化为代数问题.可以看出，不同知识的关联性与相通性是将数学基本知识转化为数学基本技能是数学解题的关键，也是数学核心素养的体现.

思路三：构造A字形相似.

分析：由切线及坐标轴知AC∥PO，延长PA与x轴交于点M，则出现“A字形”，再运用相似与一次函数的性质或相似与勾股定理或相似与三角函数知识来解答.

方法六：A字形+一次函数.

解：如图8，连接AB，AC，延长PA交x轴于点M.

图8

设CM=4x，则AM=5x.

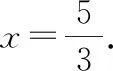
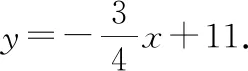
令x=0，则y=11.

所以点P的坐标为(0，11).

方法七：A字形+勾股定理.

解：如图8，连接AB，AC，延长PA交x轴于点M.

所以点P的坐标为(0，11).

方法八：A字形+三角函数.

解：如图8，连接AB，AC，延长PA交x轴于点M.

点评：平面直角坐标系蕴含有直角的天然条件，与坐标结合，可以运用函数图象；与圆的切线结合，出现直角，会产生平行线，我们自然想到延长PA，出现A字形，这也是最为经典与常见的相似基本模型.方法六将相似与一次函数结合，解法超凡脱俗，富有灵气；方法七将相似与勾股定理结合，解法经典，中规中矩；方法八将相似与三角函数结合，解答简单，让人回味.

4 教学反思

在平时教学中，不少教师选择最优解法，用最少的时间去讲解作业或试卷中的试题，很少肯花时间让学生思考，学生当时听后，觉得易懂，但遇到陌生的“生僻”的问题又找不到行之有效的解题方法，这样循环往复，教师就觉得学生“笨”，“怎么讲过的还是不会做？”因此，在平时解题活动中，教师要对典型题，包括选择题、填空题进行深度探究；要舍得花时间去思考分析，注重思考的过程、分析的途径，比如，这些条件是如何与求解结论联系起来的，是通过哪条线、哪个角进行转化的，为什么可以这样作辅助线.解题后学生要进行反思、总结：当时是如何想的？为什么老师这样解答？这样的解题方式对以后的解题有什么帮助？要进行一题多解、一题多变、多解归一等变式训练，注重积累解题经验.

正如《义务教育数学课程标准》强调：“数学活动经验的积累是提高学生素养的重要标志.”深刻探究就要让学生经历操作、思考、推理、反思等过程，对数学知识加强领会与感悟，并积累分析和解决问题的基本经验，进而把这些经验迁移到后续的数学学习中去，不断提高数学素养.