预制装配式混凝土斗栱节点抗震性能优化设计*

司建辉，胡囝楠，李 凡，午泽伟，周 明，俱军鹏，牛晓宇，贺黎哲

(1.西安理工大学土木建筑工程学院，陕西 西安 710048; 2.陕西古建园林建设有限公司，陕西 西安 710065)

0 引言

斗栱是中国古代建筑中特有的一种结构，它位于立柱顶、额枋和屋檩间，由枋上加的一层层探出成弓形的承重结构叫拱，拱与拱之间垫的方形木块叫斗，合称斗栱[1-4]。仿古建筑是现当代设计建造、体现中国传统建筑风貌的建筑通称[5]，其中仿古斗栱更是集结构功能与装饰功能于一体的结构构件。目前国内外学者对其抗震性能[6-10]开展了大量研究。薛建阳等[11-12]在试验的基础上采用ABAQUS有限元软件建立三维模型分别研究钢结构与木结构仿古建筑中斗栱的力学性能。赵均海等[13-14]对斗栱节点进行了相应的动力试验探究，研究了斗栱节点模型的频响曲线、固有频率及阻尼比，也探究了相应的边界条件、竖向荷载等对于这些部分产生的影响，同时将榫卯和斗栱简化为变刚性连接，讨论了变刚度单元刚度系数的影响。高大峰等[15-16]通过对3个缩尺比的斗栱进行水平荷载作用下的试验研究，讨论了中国古代木结构斗栱在竖向地震作用下隔震、减震机理及相应竖向极限承载能力。现阶段国内对仿古建筑的市场需求日益增加，出现了大量的混凝土斗栱结构形式，但目前对混凝土斗栱的抗震性能研究甚少。

本文基于预制装配式混凝土斗栱节点抗震性能试验建立了有限元模型，并开展斗栱节点在低周往复荷载作用下的数值仿真分析。针对加载过程中的薄弱部位(坐斗)，提出了钢纤维混凝土坐斗模型，定量分析了不同钢纤维体积率时坐斗的应力、应变特性及加固效果，可为实际工程提供参考依据。

1 试验概况

1.1 试验设计

试验按照实际工程设计了5个预制装配式斗栱节点足尺模型，均按实际尺寸1∶1进行放样。预制斗栱的底模板、侧模板均采用竹胶板包裹。侧模采用“侧板包底板”的组合拼接形式，确保了棱角部位拼接密实且易脱模，挡头模板上应预留钢筋孔。预制装配式斗栱按照构造进行配筋，后采用振动棒振捣浇筑混凝土。当构件混凝土强度达到设计强度的70%后可拆模，模板拆除应按照组装的顺序反向进行。

预制装配式混凝土斗栱安装时将第1层坐斗放在平坦处，用水泥砂浆连接坐斗与额枋；第2层包括翘与正心瓜栱；第3层是头昂、单材瓜栱与正心万栱；第4层包括耍头、厢栱与单材万栱。每层栱之间用水泥砂浆连接，使其成为一个整体。同时，将栱构件预留钢筋与柱钢筋焊接。安装过程中注意保持水平高低位置准确，各层构件之间结合严实。混凝土斗栱预制件的组合形式如图1所示。

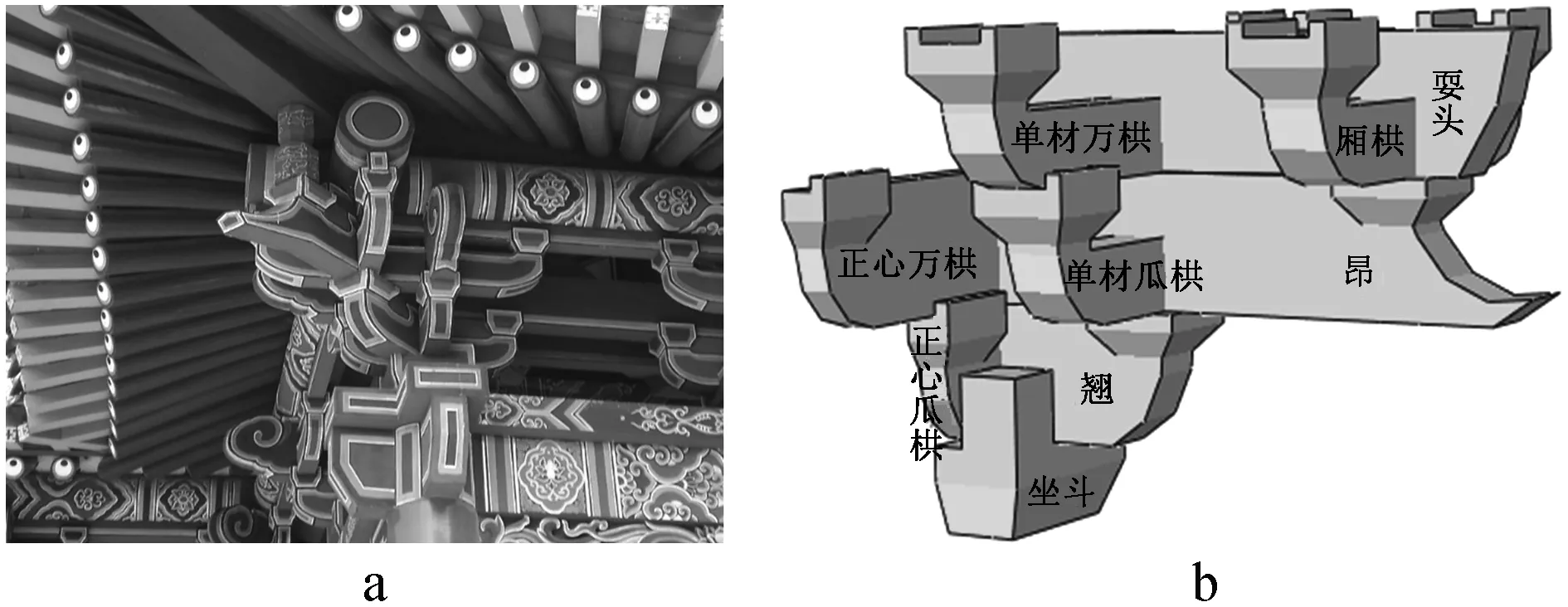
图1 混凝土斗栱预制件组合形式

试验主要研究不同轴压比及斗栱上部不同配重对其抗震性能的影响，试件分组参数如表1所示。预制斗栱节点分为两部分浇筑，首先浇筑基础及梁，用以放置斗栱坐斗；待初凝后安装混凝土斗栱，将混凝土斗栱钢筋与混凝土柱钢筋笼焊接后，再进行第2次浇筑。混凝土柱上的应变片分别布置在位于柱中上部、中部与中下部的纵筋与箍筋上，斗栱上的应变片布置在翘与昂伸出的钢筋上。斗栱节点截面尺寸与应变片布置如图2所示。

表1 试件参数

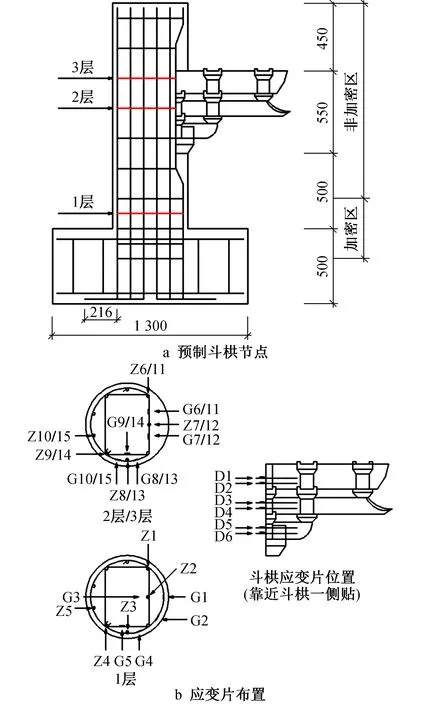
图2 预制斗栱节点及应变片布置

预制斗栱采用C35混凝土，参考GB/T 50081—2002《普通混凝土力学性能试验方法标准》，在西安理工大学建材实验室实测同条件养护下的混凝土立方体试块3组，得到混凝土立方体平均抗压强度为37.8MPa。节点处混凝土柱长1.5m，保护层厚度为30mm。纵筋采用10φ16的HRB335级钢筋；箍筋采用φ8@100/200的HPB300级钢筋。其余具体材料参数如表2所示。

表2 材料参数

1.2 加载装置与数据采集

试验采用MTS伺服加载系统进行低周反复加载试验，以位移控制的加载方式进行。在试验前对试件进行2mm的预加载，检查装置是否正常工作。正式加载的初始位移为1mm，每级以1mm作为单位增量，未屈服状态下每级位移循环 1次，而屈服后则需要循环3次，直到试件承载力下降至峰值荷载的85%时为试件破坏标志。试验过程中应及时有效记录裂缝出现与相应的延伸现象。应变数据采集装置采用DH3815静态数据采集仪。试件加载装置如图3所示，加载制度如图4所示。

图3 加载装置

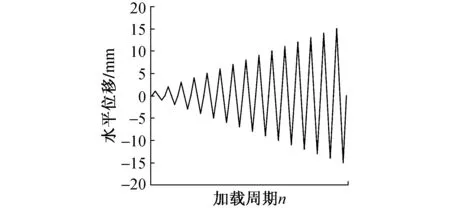
图4 加载制度

1.3 破坏形态

预制斗栱试件在加载初期水平位移较小，试件表面没有明显变形。随着水平位移的增加，斗栱坐斗处首先出现竖向微裂缝。随后混凝土柱也产生了横向裂缝，此时水平位移已达到峰值位移的45%。坐斗处的竖向裂缝发展迅速且缝宽增大，同时在昂与翘的两侧也出现了一些微小细裂缝。试件在低周往复荷载作用下，混凝土柱的横向裂缝不断张开闭合，最后贯通。继续施加位移，柱底部的混凝土保护层有明显的脱落趋势。当承载力下降至峰值荷载的85%时停止加载。

首先出现破坏的为坐斗处，原因是斗栱穿插在钢筋混凝土柱中，当柱顶部施加水平位移时，钢筋混凝土柱底部截面处产生的内力，需要钢筋混凝土柱与坐斗二者共同承载，考虑到二者协调变形，且后者被放置于前者的外层，因此坐斗变形明显比钢筋混凝土柱的大，坐斗最开始发生破坏，之后柱底部截面处的内力仅由钢筋混凝土柱承受，钢筋混凝土柱底部随之发生破坏。坐斗自身的开裂主要是因为坐斗本身是素混凝土结构，其承载力被大大削减，抗拉、抗弯性能较弱，在施加位移的过程中会发生脆性破坏。

2 ABAQUS有限元模型

通过观察预制装配式混凝土斗栱节点在水平往复荷载作用下的破坏形态可知，斗栱坐斗是结构最薄弱部位，且坐斗自身的开裂主要是因为其本身是素混凝土结构，缺乏足够的抗拉、抗弯性能，在施加位移的过程中会发生脆性破坏。由于试验场地与资金的限制，仅在数值仿真模拟软件中对混凝土斗栱节点的坐斗部位进行补强优化设计，选取试件三维有限元模拟样本，将试件的素混凝土坐斗替换为钢纤维混凝土坐斗，并对混凝土斗栱节点的抗震性能进行数值仿真分析。

2.1 材料本构关系

混凝土采用ABAQUS模型库中的塑性损伤模型(plasticity damage model)。轴压应力-应变关系曲线根据GB 50010—2010《混凝土结构设计规范》(2015年版)中的相关表达式确定：

σ=(1-dc)Ecε

(1)

(2)

式中：αc为曲线上升段、下降段的参数值；fc,r,εc,r为混凝土轴压强度、峰值压应变；dc为受压损伤演化参数；ρc=fc,r/Ecεc,r;n=Ecεc,r/(Ecεc,r-fc,r);x=ε/εc,r。

单轴受拉应力-应变关系曲线表达式：

σ=(1-dt)Ecε

(3)

(4)

式中：αt为曲线上升段、下降段的参数值；ft,r,εt,r为单轴受拉强度、最大拉应变；dt为受拉损伤演化参数；x=ε/εt,r;ρt=ft,r/Etεt,r，未实测数值均根据《混凝土结构设计规范》(2015年版)确定。

各参数值的计算方法规范已给出，但对于钢纤维混凝土结构，部分公式计算值并不准确。因此参考文献[17]所提出的计算方法，部分参数表达式如下：

(5)

αc=0.132fcu0.875-0.905

(6)

钢筋本构选用理想的钢筋弹塑性，两者的本构关系曲线如图5所示。

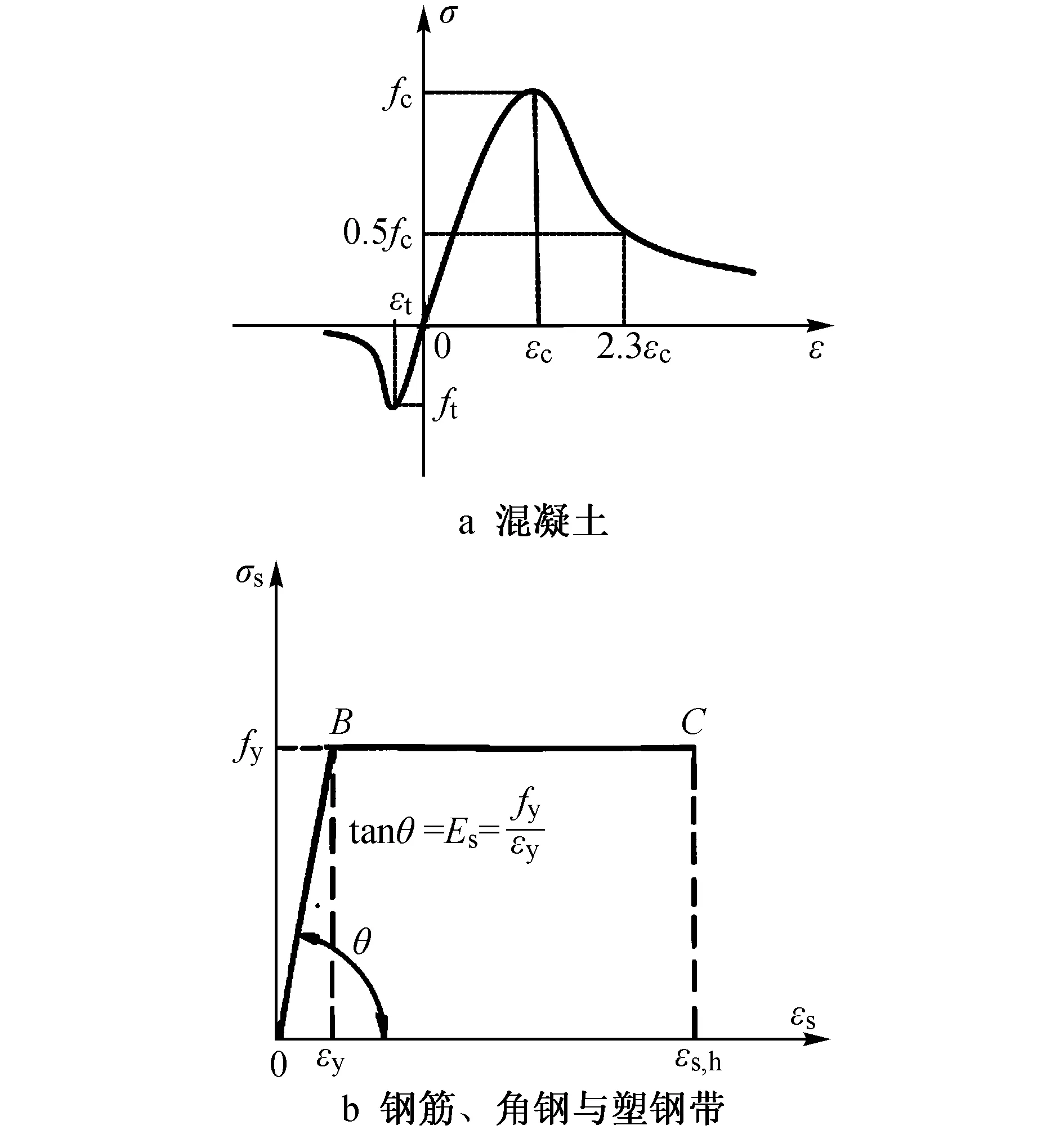
图5 本构关系曲线

2.2 单元选取

在建模过程中，混凝土采用C3D8R实体单元(8节点的六面体线性减缩积分单元)。钢筋骨架统一采用2节点三维桁架实体单元，构件模型如图6所示。

图6 构件模型示意

2.3 相互关系

钢筋骨架与混凝土采用嵌入接触，假定两者之间不产生相对滑移。对于斗栱与柱之间的面与面接触采用Tie连接。同时，为了模拟斗栱的装配性特点，混凝土斗栱各层间采用面与面接触，水平向黏结系数取0.3。

2.4 边界条件与加载方式

仿真模拟中柱底部采用固定约束，设置了2个分析步，第1步用来施加竖向荷载，分别是装配式斗栱上部的配重及混凝土柱顶的轴压；第2步用来施加水平荷载，采用循环往复位移加载制度，每级循环一次，每级的增量为1mm，施加的位移值为试验过程中各循环峰值位移。

2.5 网格划分

为获取精确的计算结果与较高的计算机运算效率，对各个部件划分网格时，应通过合理布置种子来控制合适的网格密度。斗栱各构件名称及网格划分如图7所示。

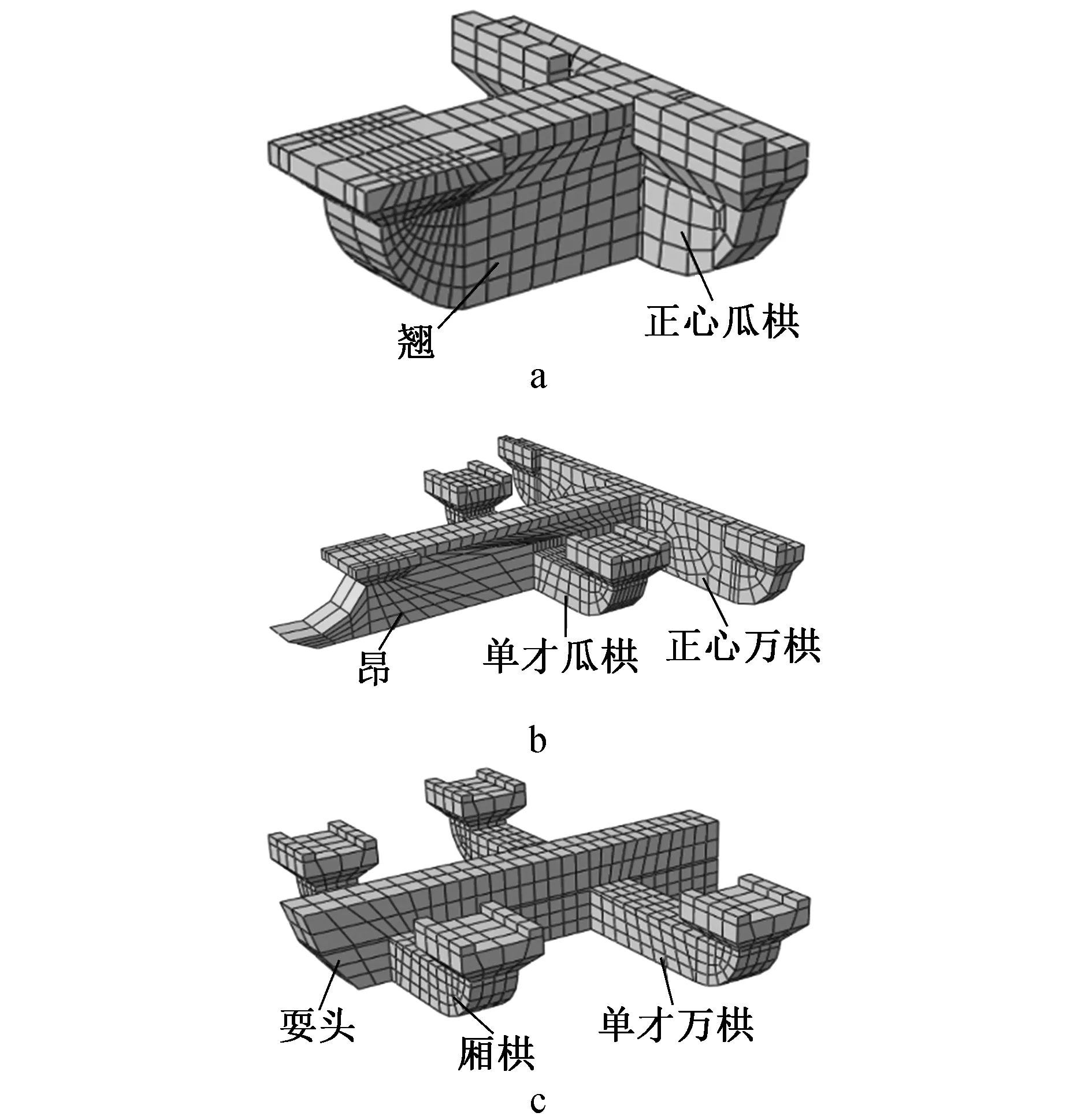
图7 斗栱各构件网格划分及名称

3 有限元结果分析

试验试件与有限元模型的滞回曲线及骨架曲线分别如图8，9所示。

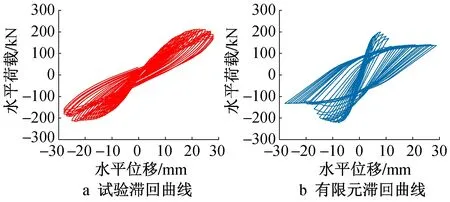
图8 试件3滞回曲线

图9 试件3骨架曲线对比

通过对比试验和有限元的滞回曲线及骨架曲线可以看出，两者极限承载力基本相当，而极限位移有一定的差异，主要是由于在有限元模型中未考虑混凝土材料的离散性，且试验时试件与加载装置存在一定的间隙，所以导致有限元计算的位移与试验位移相比有所减小。但总体来看，两者规律一致，表明有限元模型较可靠，可为下一步优化模拟分析提供基础。

斗栱各部件在荷载作用下的等效塑性应变如图10所示。

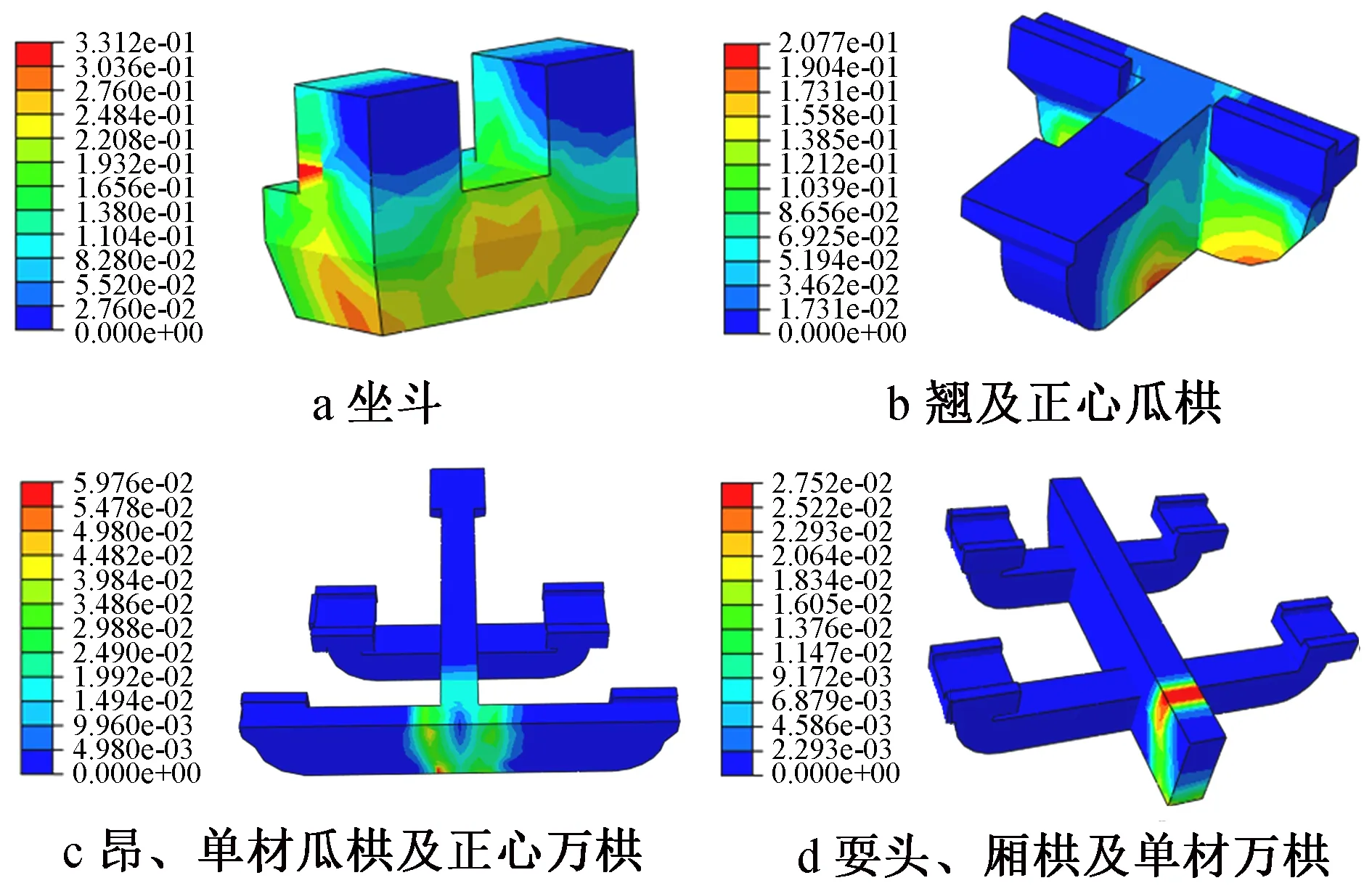
图10 斗栱的应变云图

由图10可见，极限位移下坐斗及斗栱节点区域均发生较大塑性变形，通过对比可知斗栱坐斗处最先出现塑性应变且达到极限位移时的累积变形最大，此外坐斗处的塑性应变区域较其他各层分布更广，所以构件最薄弱部位位于斗栱坐斗处，与试验结果基本一致。由试验及有限元计算可知，斗栱构件中坐斗为最薄弱构件，在荷载作用下发生了竖向及剪切破坏，因此以下章节均只对该部位进行重点讨论。

坐斗在各级荷载位移作用下的塑性应变如图11所示。

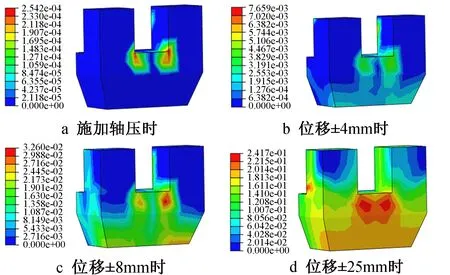
图11 坐斗塑性应变云图

由图11可见，坐斗主要发生的是竖向剪切破坏，在模拟初期给试件施加一定轴压之后，在坐斗的角隅处就开始出现塑性区。随着位移增加至±4mm时，塑性区域也随之增大，且由斗耳处向下扩展，当位移加至±8mm时，坐斗底部的受压区混凝土塑性逐渐增大，使与斗耳处受剪区混凝土相接，坐斗塑性应变区域增大。当到达极限位移时，两侧斗耳处受剪区的混凝土塑性应变增大至最大，塑性应变区域贯通，坐斗受压区的塑性应变逐渐增大，最后受压区混凝土被压碎，坐斗破坏。

4 配置不同体积率钢纤维对坐斗抗震性能的影响

试验及有限元模拟分析结果均表明斗栱最薄弱部位位于坐斗处，需对坐斗进行加强处理，因该构件所在位置的特殊性，对其进行配筋在预制及施工过程中均难以处理，故提出了钢纤维混凝土坐斗模型，由于钢纤维能有效地提高混凝土的韧性与强度，且能成批生产，在价格方面较经济，施工较方便，所以采用钢纤维来增强混凝土的性能是一种非常有效的手段。

4.1 试件设计

由于在实际工程中钢纤维对结构加固能起到一定作用，且构件中掺入钢纤维的体积率宜在2%以内，故本节有限元分析模拟4组试件(Z-1，Z-2，Z-3，Z-4)，分别表示坐斗中掺入钢纤维的体积率为0%，0.5%，1%，1.5%的试件，轴压比为0.4，斗栱配重为200kg。

4.2 最大主拉应力分析

通过分析不同钢纤维体积率坐斗的最大主拉应力和塑性应变，来研究坐斗在不同体积率钢纤维加固作用下，自身应力应变的变化及分布情况。不同钢纤维体积率下坐斗的最大主应力如图12～15，表3所示。

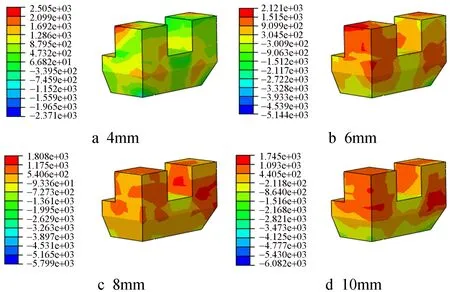
图12 混凝土坐斗的应力云图

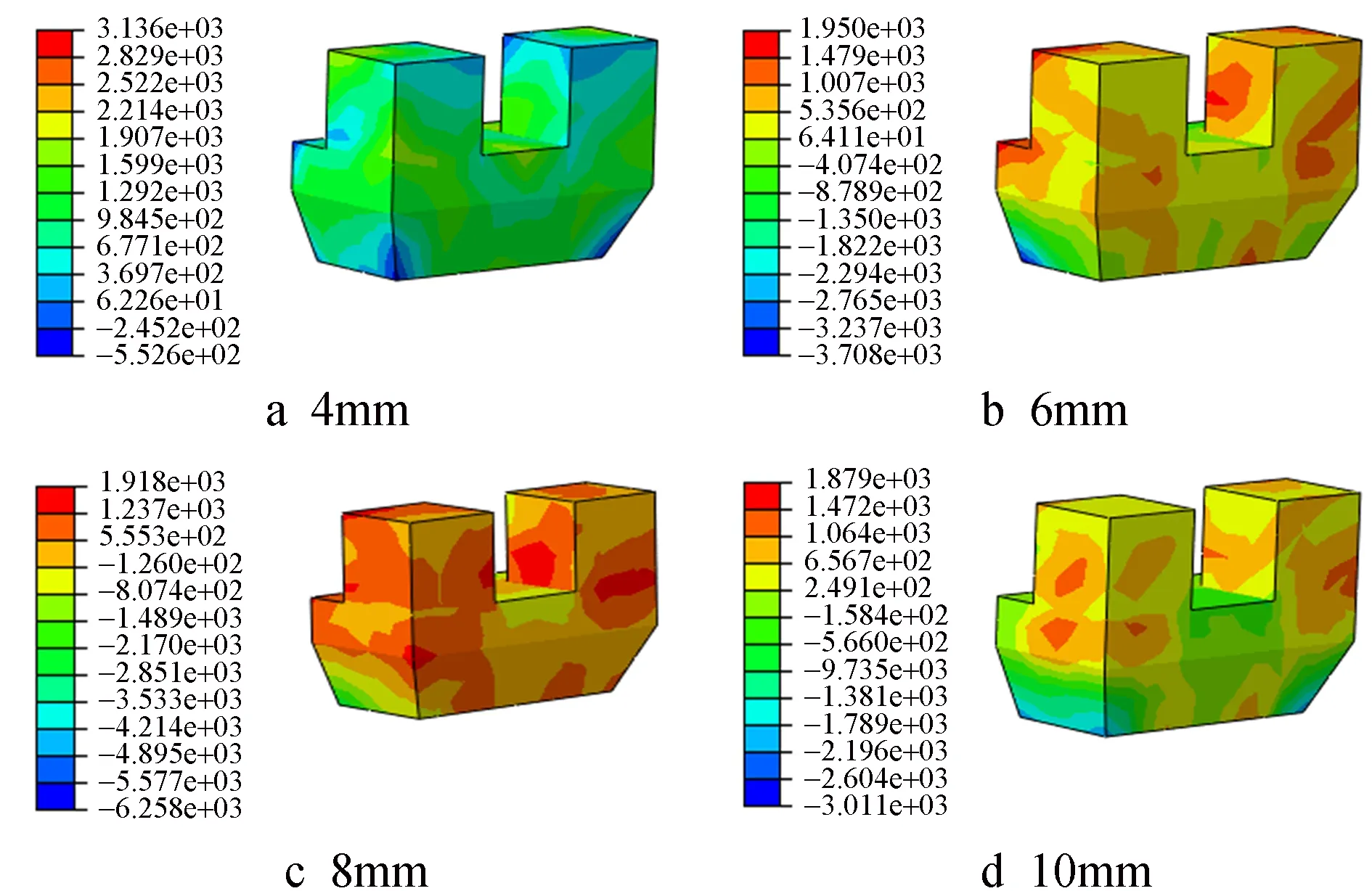
图13 钢纤维体积率为0.5%坐斗的应力云图

图14 钢纤维体积率为1.0%坐斗的应力云图

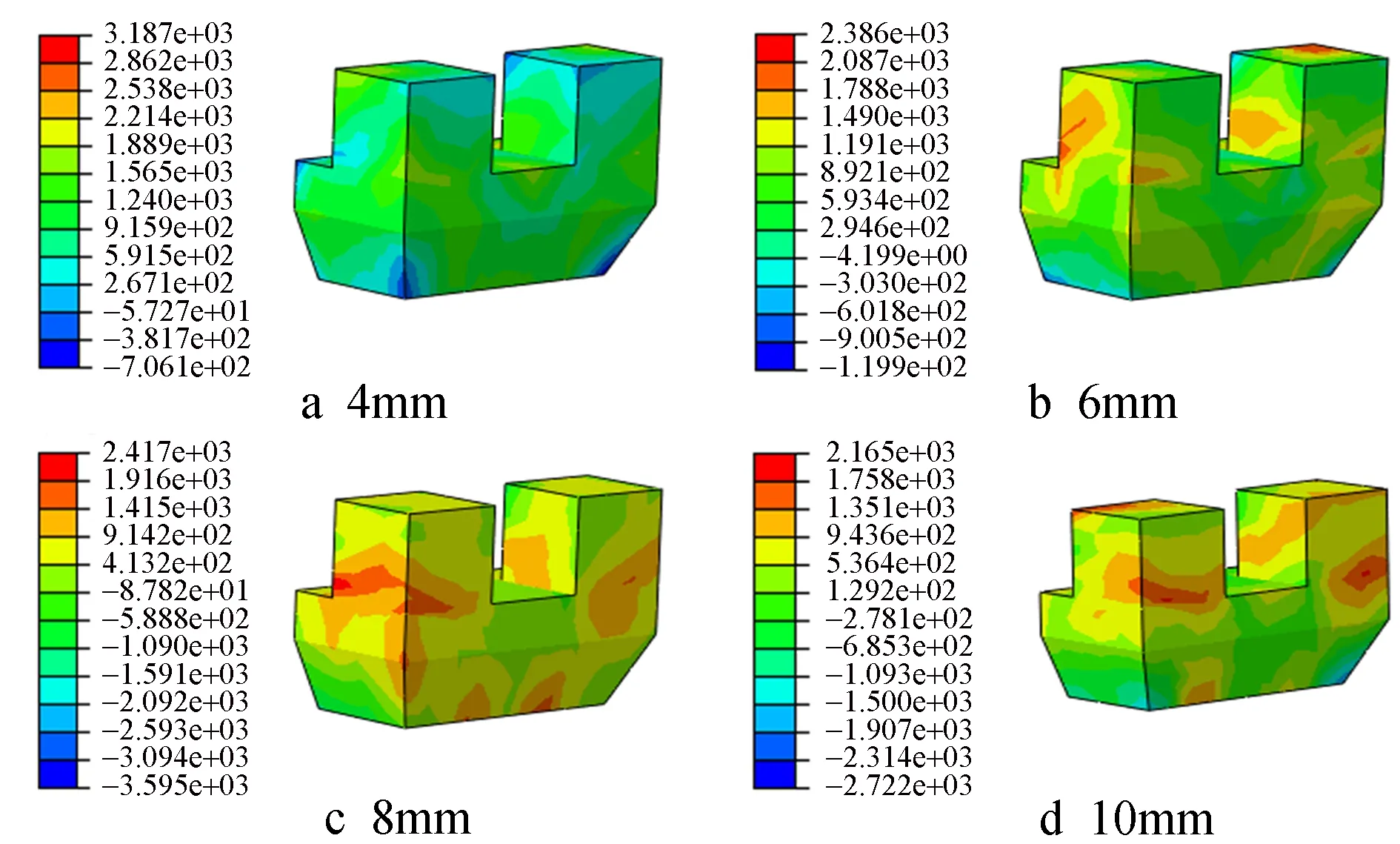
图15 钢纤维体积率为1.5%坐斗的应力云图

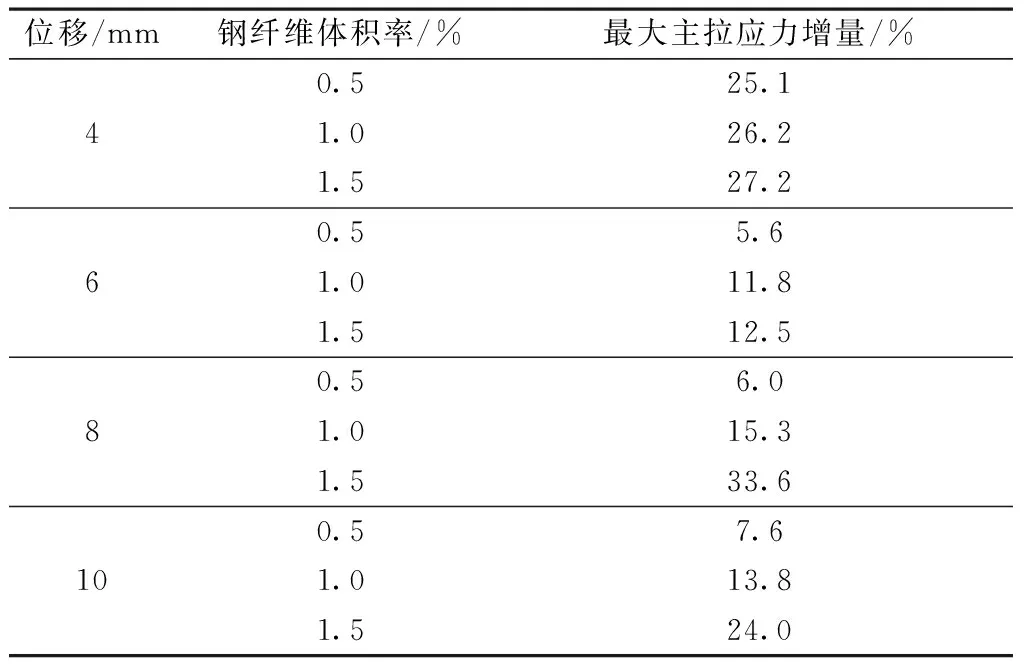
表3 不同体积率钢纤维时坐斗的最大主拉应力增量

由图12～15与表3可知，混凝土坐斗与钢纤维混凝土坐斗随着加载位移的增加，坐斗处的最大主拉应力反而越小，该结果主要是由于坐斗开裂造成的，位移增加使坐斗开裂越来越严重，使坐斗所承担的拉力减小。

当位移为4mm时，掺入不同体积率钢纤维坐斗的最大主拉应力相较于素混凝土分别提高了25.1%，26.2%，27.2%；位移增加至8mm时掺入钢纤维坐斗的最大主拉应力分别提高了6%，15.3%，33.6%；位移继续增大，10mm时不同体积率的钢纤维混凝土坐斗分别提高了7.6%，13.8%，24%。由有限元数值模拟结果可得，当斗栱坐斗掺入合理的钢纤维(钢纤维体积率不超过2%)时，坐斗处的抗拉强度和抗剪强度均能得到有效提高，且随着钢纤维体积率的逐渐提高而显著增强。坐斗处的破坏由最初的脆性破坏形式变为近似于延性断裂的破坏形式。

4.3 塑性应变分析

不同纤维体积率下的塑性应变如图16～19所示。

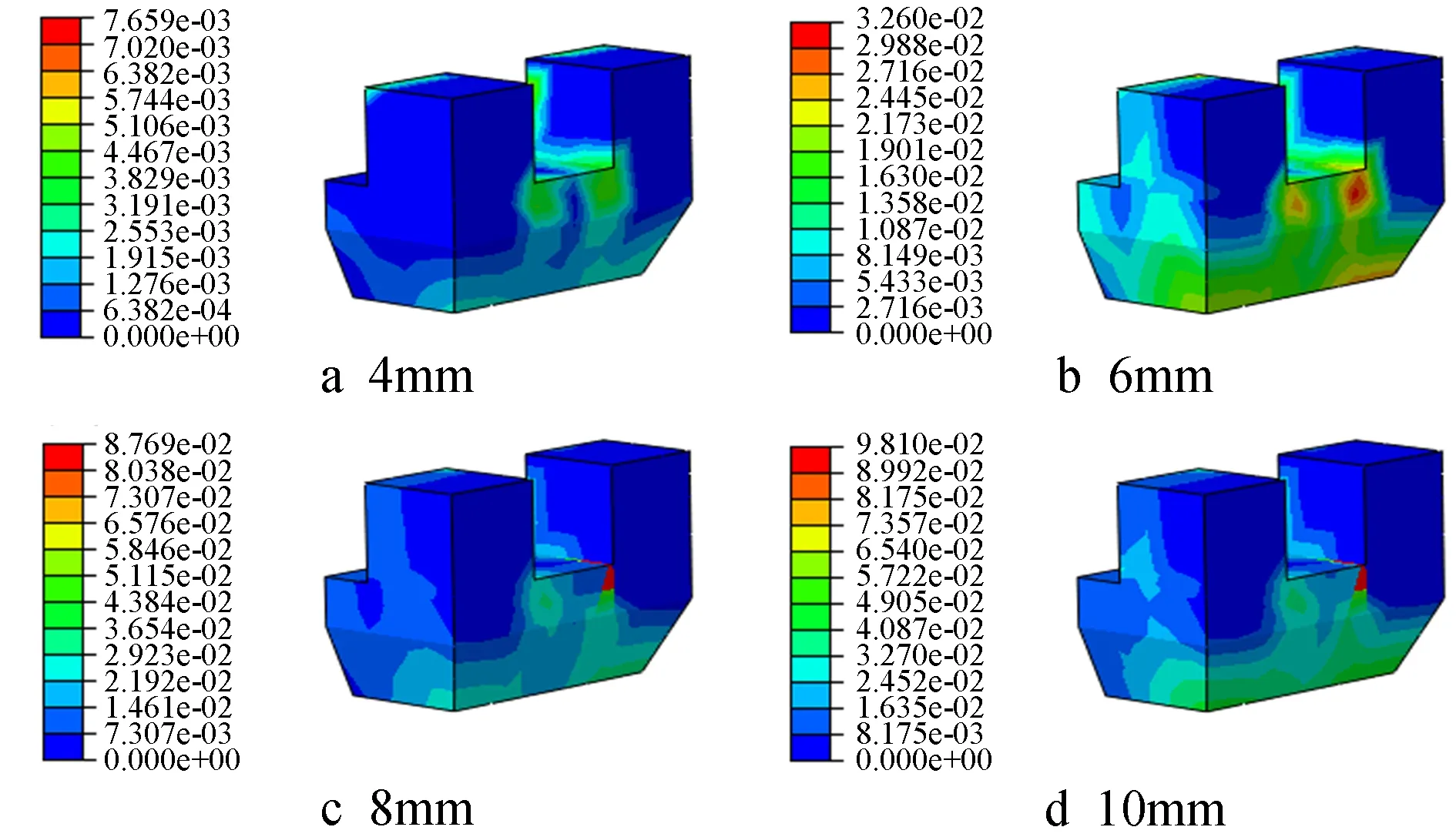
图16 混凝土坐斗的应变云图

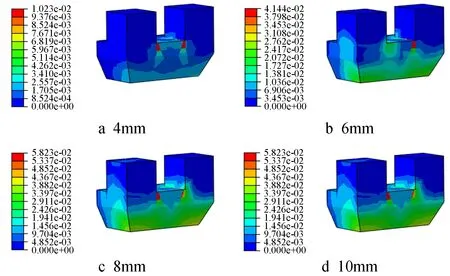
图17 钢纤维体积率为0.5%坐斗的应变云图

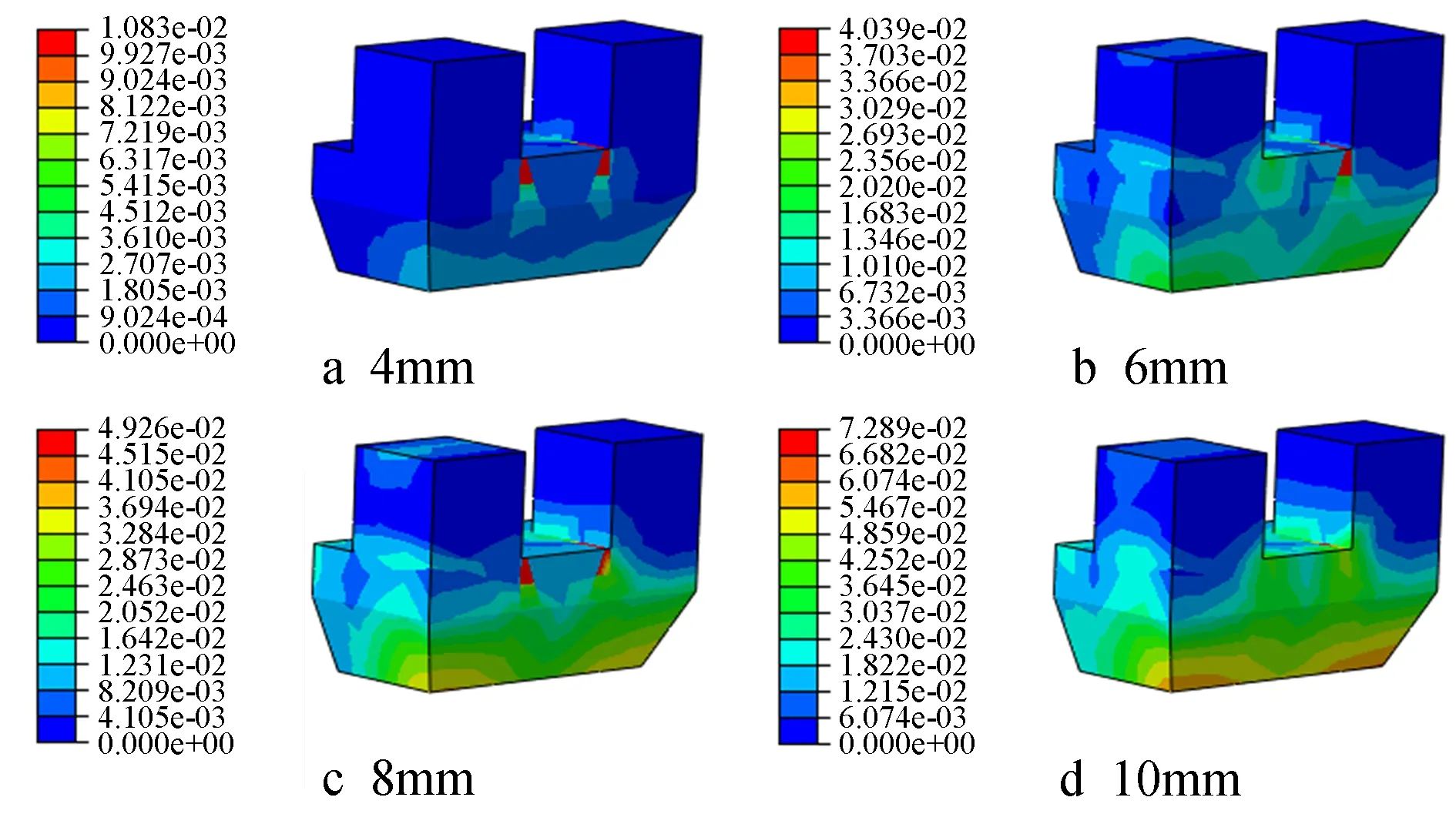
图18 钢纤维体积率为1.0%坐斗的应变云图

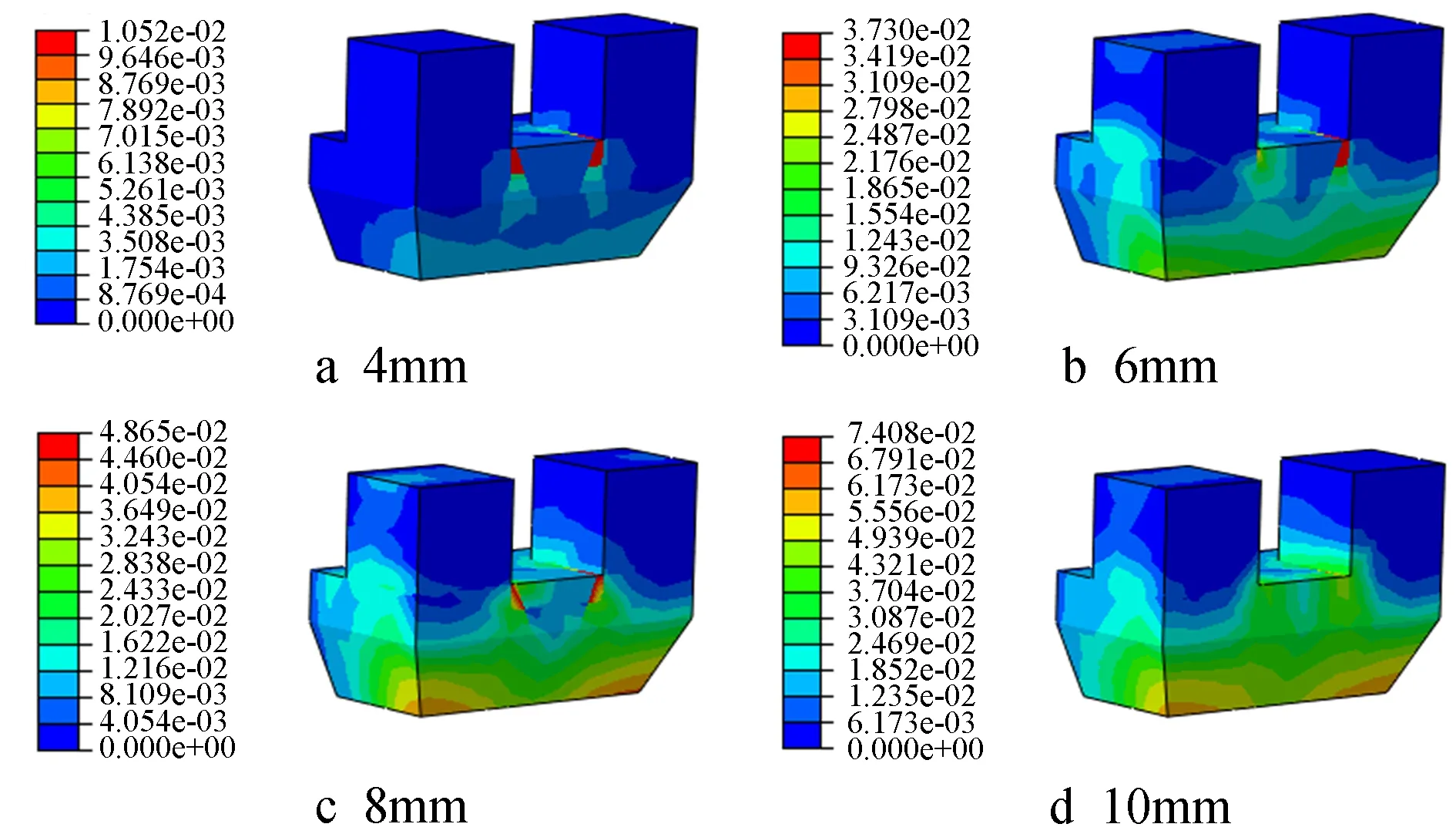
图19 钢纤维体积率为1.5%坐斗的应变云图

由图16～19可知，坐斗在两种不同材料的作用下，塑性应变区域均随位移的增加而逐渐变大，且相同位移时混凝土坐斗的塑性应变区域比钢纤维混凝土坐斗的大，表明钢纤维在一定程度上对混凝土起到了约束作用，能有效地控制坐斗塑性应变的发展。不同体积率钢纤维时坐斗的塑性应变增量如表4所示。

表4 不同体积率钢纤维时坐斗的塑性应变增量

由表4可知，坐斗处塑性应变增量有正值也有负值，即在坐斗开裂之前素混凝土的塑性应变要比钢纤维混凝土的稍小，主要是由于加载初期，坐斗部位为钢纤维混凝土，刚度较大，受力也较大，导致塑性应变也较素混凝土坐斗大，随着位移增加，钢纤维混凝土的塑性应变开始小于普通混凝土，表明素混凝土坐斗破坏要早于钢纤维混凝土坐斗。

整体来看，钢纤维混凝土的塑性变形要小于普通混凝土。故当坐斗掺入合理的钢纤维时，坐斗的塑性应变量明显减小，由此说明钢纤维对坐斗塑性应变的发展能起到积极的约束作用，且能有效降低坐斗的初裂荷载。

5 结语

1)坐斗本身是素混凝土结构，虽然有一定的抗压强度，但是抗拉强度很差，试验过程中最先发生破坏。针对该问题，提出了钢纤维混凝土坐斗模型。

2)以坐斗中掺入不同体积率的钢纤维为研究参数，在轴压比与配重相同的条件下，掺入合理的钢纤维(钢纤维体积率不超过2%)时，坐斗处的抗拉强度和抗剪强度都能得到有效提高，且随着钢纤维体积率的逐渐提高而显著增强，钢纤维混凝土坐斗的塑性应变小于普通混凝土，掺入合理的钢纤维能有效阻止坐斗开裂，可为预制装配式斗栱结构设计提供参考。