一种面向机器人机械系统的程式化动力学建模方法

庄 未， 康文杰， 黄用华， 高振宇， 杨继伟

(桂林电子科技大学 机电工程学院，广西 桂林 541004)

复杂系统动力学模型是进行运动控制的重要基础，而动力学建模方法在很大程度上决定了模型的准确性和计算效率，从而影响控制效果，因此受到了许多学者的广泛关注。

近年来，机器人动力学建模方法主要有2种。第一种方法为基于分析系统力和力矩矢量的建模方法，其属于牛顿经典力学范畴，例如牛顿-欧拉(NE)法和Kane方法。Kvrgic等[1]认为NE法是推导机械臂动力学模型的一种非常有效的计算方法，且将该方法应用于六自由度机器人，并与其他方法的计算效率进行比较。王健等[2]根据NE法建立了四旋翼飞行器的非线性模型并设计控制器，实现了对四旋翼飞行器系统双环控制。赵丽美[3]和Ghariblu等[4]采用NE法分别建立蛇形机器人和新型移动球形机器人动力学模型，均实现了基于模型的运动控制研究，特别是后者提出的动力学方程中有关微分代数方程的计算方法。Luh等[5]开发出一种效率更高的递归NE法，独立于机器人配置的类型，文献[6-8]中有着许多类似的应用。Kane方法综合分析力学和矢量力学的优点，以“广义速率”取代“广义坐标”作为独立变量，引入偏速度、偏角速度独特概念，着手于广义主动力、广义惯性力的计算。Hussain等[9]认为Kane方法优于NE法和Lagrange方法，并利用Kane方法建立了三自由度机构运动链的动力学模型，可为研究Kane方法的初学者提供指导性意见。Huang等[10]采用Kane方程以螺旋理论的形式建立了前轮驱动自行车机器人的动力学模型，为其他类似非完整约束系统建模提供了参考。Kane等[11]建立了基于Kane方程的六自由度斯坦福机械臂的动力学模型，与NE法建立的模型在运算次数上作比较，结果表明Kane方法计算效率更高。庄未等[12]采用同样的方法建立了球形机器人的动力学模型，并完成了直线和S曲线运动的仿真分析。

第二种是基于分析系统能量和功的建模方法，即属于分析力学范畴，如基于Chaplygin方程或L-agrange方程的建模方法。Zhang等[13]采用Lagran-ge方程建立球形机器人动力学模型，实现了对整个系统的实时控制。Ruan等[14]利用Euler-Lagrange方程对独轮车机器人进行建模，并完成了一系列的实验。李梦飞[15]基于Lagrange方程建立了六自由度机械臂的动力学模型，并通过ADAMS动力学仿真验证了模型的正确性。文献[16-19]给出了Lagrange方程在其他机械臂及多自由度机器人上的应用。对于欠驱动非完整约束系统，在文献[20-21]中应用Lag-range方程的另一种形式Chaplygin方程分别建立了变结构两轮车机器人和独轮车机器人的动力学模型，并完成了一系列仿真分析和物理样机实验。

通过对上述文献中关于动力学建模方法的研究可知，牛顿经典力学分析过程繁杂，会产生大量的约束反力，对于复杂的力学系统，其难以直接应用；基于能量分析的方法，随着自由度的增加，其模型输出容易产生横向膨胀，导致偏导数、导数计算难以进行，即所谓的维数灾难，带来重复计算、运行效率低下的问题。

鉴于此，提出一种程式化建模方法(programmed modeling method,简称PMM)，通过对系统运动学的正向分析和系统动力学模型的逆序输出，解决了建模过程中模型复杂、输出膨胀等问题。

1 方法描述

传统建模方法从系统广义坐标逐步计算动力学方程所需元素，然而建模过程实则是符号计算的过程，这将使变量表达式被层层迭代，容易导致模型输出膨胀。PMM解决了这一问题，其大体分为系统运动学的正向分析和系统动力学模型的逆序输出2个步骤。正向分析是对所研究对象的系统分析，包括坐标系分析、角速度和质心速度分析、运动约束分析、动能和力函数分析、变量蕴含关系分析等；逆序输出是指将动力学方程所需元素的计算结果按逆序输出，确保模型不膨胀。图1为PMM总体思路示意。

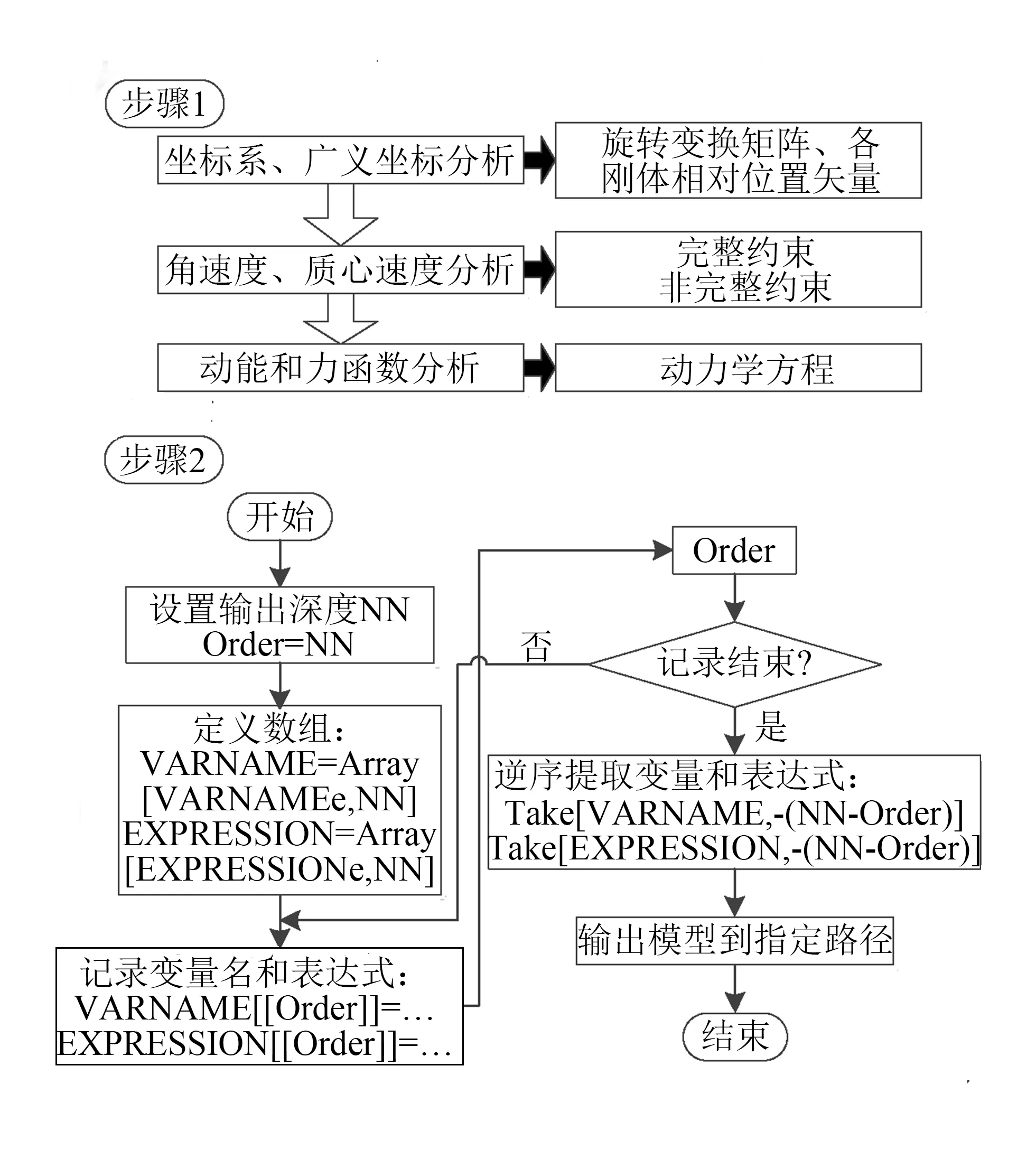
图1 PMM总体思路

PMM的核心思想：正向分析开始于广义坐标，中间包括速度、非完整约束分析等，终止于系统的动能和势能，其关键在于引入中间变量后建立变量的隶属关系表；逆序输出始于动能(势能)对广义坐标或广义速度的偏导数，通过变量隶属关系，根据链式求导的方法逐步传播扩散，最终分析出最原始、最基本的偏导数项，并按链式求导时先后顺序的逆序进行输出。

在实际建模过程中，以上技术手段尚不能完全保证输出最合理、最简洁的力学模型，有时会遇到0变量、变量重复定义和顺序错乱等问题，图2所示算法用以解决上述问题。

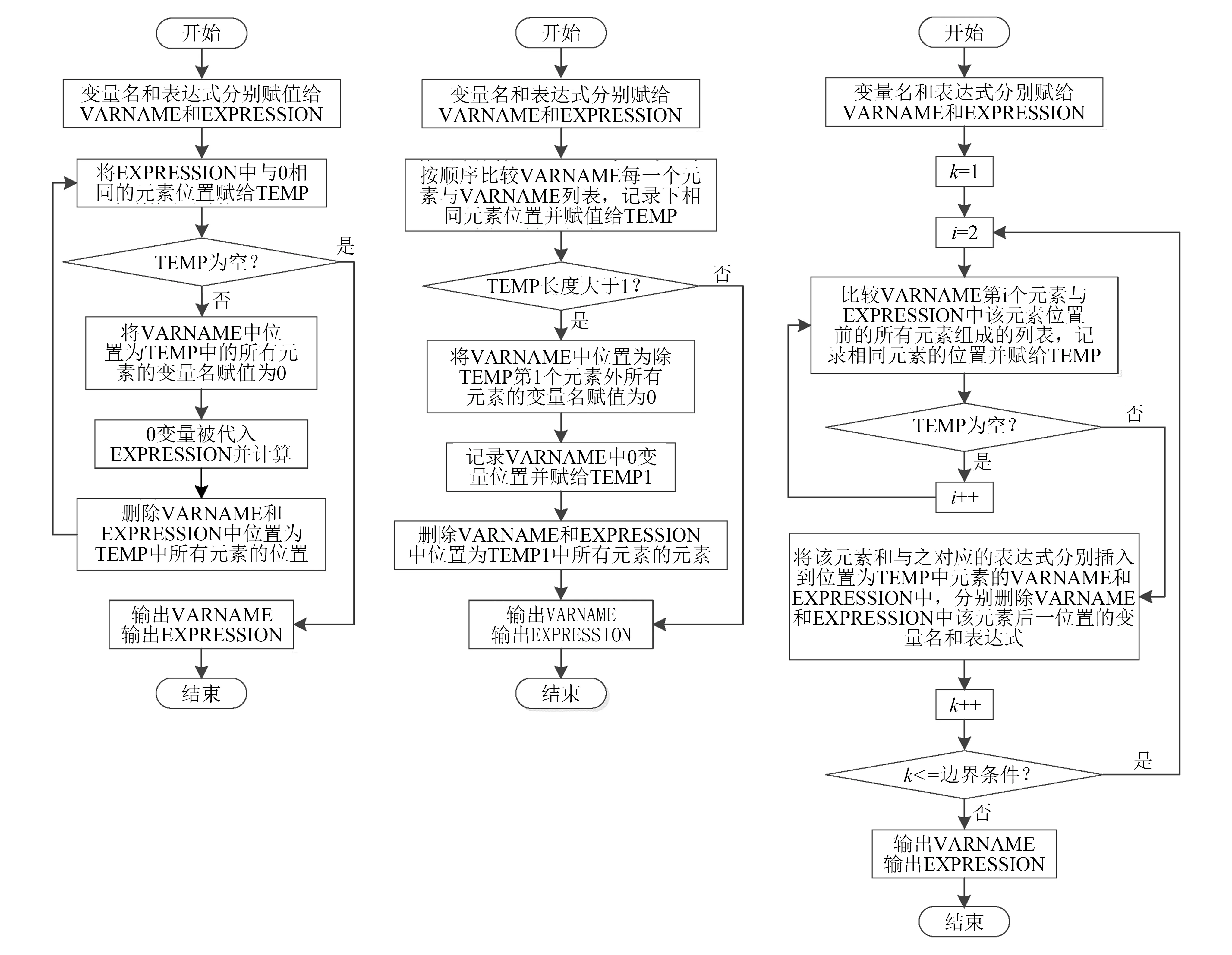
图2 剔除0变量、剔除重复变量及变量排序算法流程

2 斯坦福机械臂建模与仿真分析

为更加直观地介绍PMM和说明其高效性，应用该方法建立斯坦福机械臂动力学模型[11]，机构简图如图3所示。

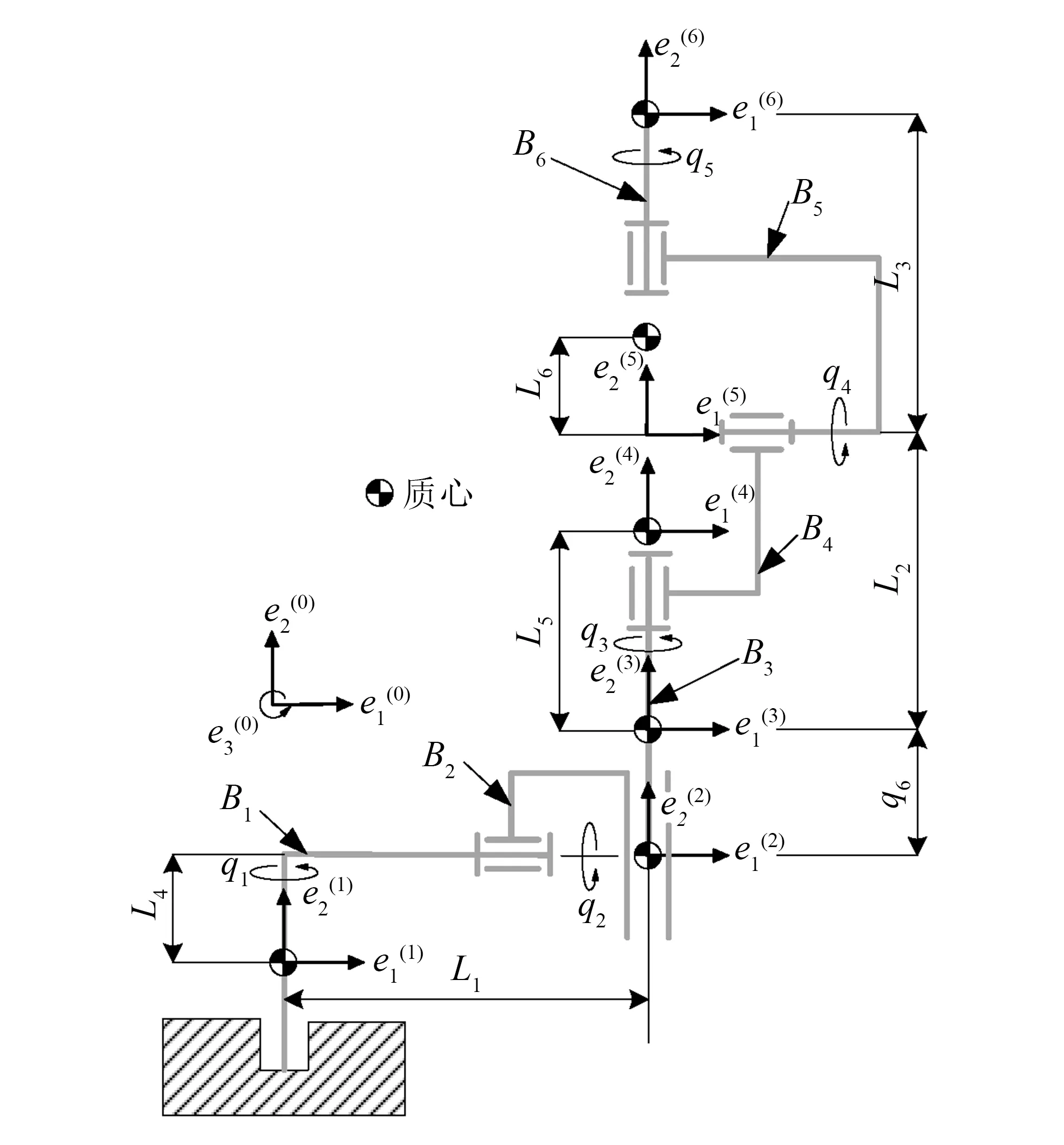
图3 斯坦福机械臂机构

它由6个构件组成，分别记为Bi(i=1～6)，B3通过滑动副与B2相连，以实现平移运动；B2、B4、B6通过相应旋转关节分别与B1、B3、B5相连，作定轴转动。

坐标系及广义坐标描述：

1)ej(i)，i、j=1～3，表示Bi坐标系x、y、z轴；

2)e(0)为大地坐标系，e2(0)始终与地面垂直；

3)初始时刻，各坐标系轴与大地坐标系轴方向一致，坐标系e(2)与e(3)原点重合；

4)选取qi，i=1～6，表示系统的6个广义坐标。

建模过程中所使用的符号及含义如表1所示。特别说明，k、m、n均属于i。

表1 系统变量定义

2.1 正向分析过程

根据机器人学公式可知，e(0)转换为e(4)的旋转变换矩阵：

(1)

其中，Rot(p, -qj)(p=x,y;j=1～3)为绕P轴转-qj的旋转变换矩阵。

由刚体运动学原理可知，B4角速度

(2)

其中，ej(j=1～3)为第j个轴的单位矢量。

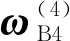
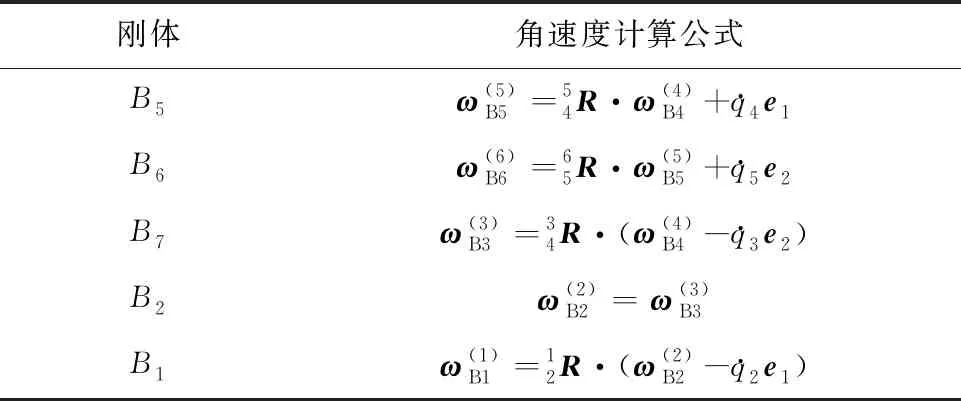
表2 刚体角速度

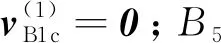
(3)

其他刚体质心速度计算公式如表3所示。

表3 刚体质心速度

由表2、3可求出系统总动能，系统各刚体动能分为转动动能和平动动能，则有

(4)

其中：Mi与Ji为三维质量矩阵，且Mi=miI，mi为各刚体质量，I为3×3单位阵；Ji=diag(Jx，Jy，Jz)，其中Jx，Jy，Jz为刚体Bi绕过质心对应的转动惯量。

以e(1)原点为零势能参考面，B5质心高度，则

(5)

注：[2]表示取矢量第二个元素，即矢量在e2轴上的投影(质心高度)。

其他刚体质心高度计算类似，求得系统总重力势能

(6)

2.2 逆序输出过程

基于拉格朗日方程的动力学模型:

(7)

其中，τi为关节驱动力矩。

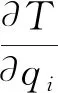
(8)

同样，分析出式(6)中各函数及变量蕴含关系，如表4所示。

表4 变量隶属关系表

由表4可知，引入中间变量后，动能T是ul(l=1～18)的函数，ul又是qi(i=2～6)的函数，根据链式求导法则有

(9)

中间变量ul中的qi除q6外均以三角函数出现，故有

(10)

其中，si=sinqi，ci=cosqi。

为避免模型膨胀及重复运算，中间变量不被代入函数或相关表达式中。具体来说，当输出式(9)时，式(10)不被代入式(9)。

2.3 仿真分析

运用Mathematic软件编写相关程序，并结合自行编写的格式转换脚本(.m文件)将模型自动输出为不同格式(.m或.c)的文件，用于MATLAB仿真或VC++环境下的控制器设计。

在仿真实验中，采用文献[11]中规划的轨迹和结构参数，以验证PMM所建斯坦福机械臂力学模型的可靠性。设置仿真时间为10s，动力学第二类问题仿真分析结果如图4所示。

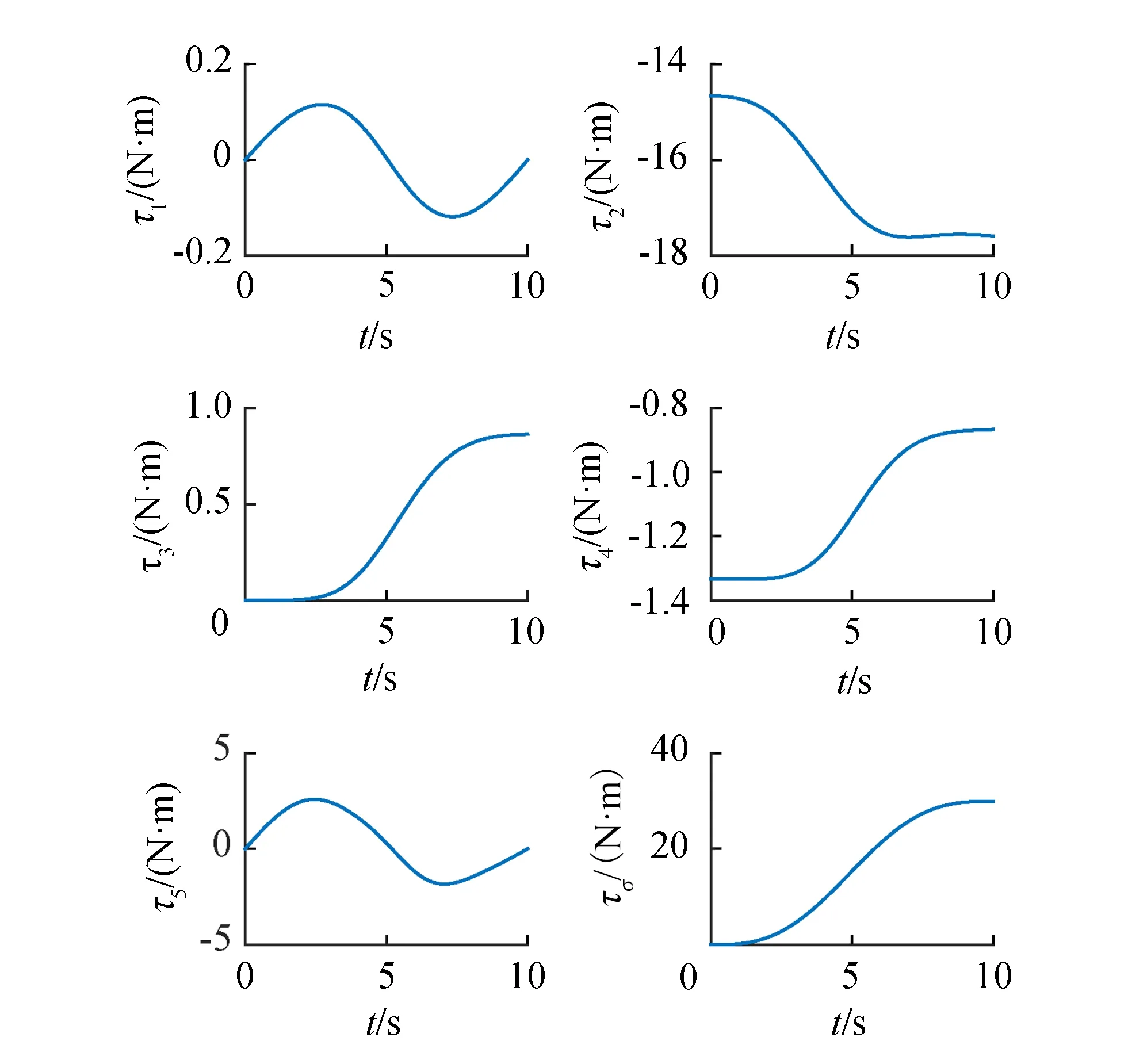
图4 斯坦福机械臂仿真曲线

从图4可看出，基于PMM建立的斯坦福机械臂动力学模型的仿真曲线与文献[11]中仿真曲线一致，验证了模型的可靠性。在此基础上，采用未使用PMM的常规Lagrange方法[15]建立斯坦福机械臂动力学模型，并做比较，如表5所示。

由表5可看出，相较于常规Lagrange法，PMM建立的斯坦福机械臂动力学模型在变量个数上增加80个，但模型“尺寸”缩减了57.9%，体现了PMM以深度换取宽度的优势；计算总操作数由11015次降为3563次，模型复杂程度降低了67.6%。2种方法建立的斯坦福机械臂模型运行在主频1.8GiB、双核CPU、2GiB内存、Win7操作系统和VC++环境的为阐明PMM适用范围和进一步验证该方法的有效性，将其推广到欠驱动非完整约束系统。

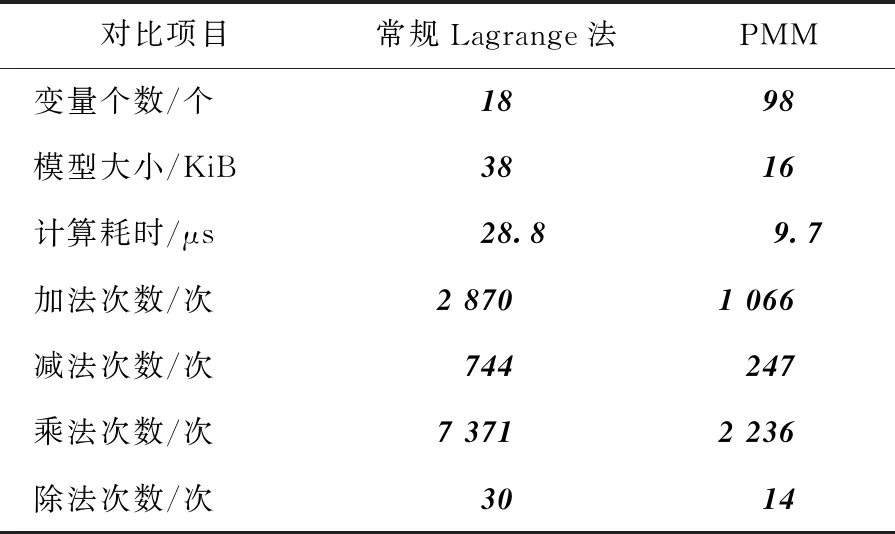
表5 PMM与常规Lagrange方法所建模型参数

工控机平台上进行10次测试，PMM所建模型平均耗时9.7μs，而常规Lagrange方法平均耗时为28.8μs，运行效率提高了66.3%。

3 PMM在欠驱动非完整约束系统的验证

变结构两轮车机器人具有静态不稳定而动态稳定的特性，是典型的欠驱动非完整约束系统。以变结构两轮车机器人原地俯仰平衡实验为例，机构简图及物理样机如图5、6所示。

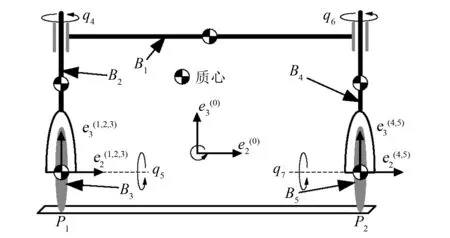
图5 机构简图

图6 物理样机

系统由车架B1、2个车叉(B2，B4)及2个车轮(B3，B5)构成，坐标系e(k)(k=1，2，3)原点均在B3质心处，e(m)(m=4，5)原点均在B5质心处，2个接地点分别为P1和P2。

实验基于PMM所建立模型和高度依赖系统模型的部分反馈线性化控制算法。车架3个欧拉角q1、q2、q3(航向角、横滚角、俯仰角)由旋转序列e3、e1、e2决定，车架俯仰角直接影响车体的平衡，取俯仰角为输入，车轮转矩为输出，于是

v=kp(q3-q3d)+kd(dq3-dq3d)，

(11)

其中：v为虚拟控制量；q3和dq3为车身俯仰角和俯仰角速度，q3d和dq3d为期望值；kp和kd为控制参数。

设计部分反馈线性化控制器，

τw=DD·v+EE，

(12)

其中：τw为车轮电机转矩；DD和EE为与模型相关变量。

基于该控制器的控制参数设定为：

数值仿真时，kp=-50，kd=1；

物理样机实验时，kp=100，kd=103。

图7、8分别给出了仿真结果和实验数据，图9为物理样机实验视频连拍图。由图7可见，车架俯仰角和车轮驱动力矩在有限时间内快速收敛到0附近。由图8、9可见，车架俯仰角在±0.02rad范围内波动，车身处于俯仰平衡，故变结构两轮车机器人实现了原地俯仰平衡控制实验。

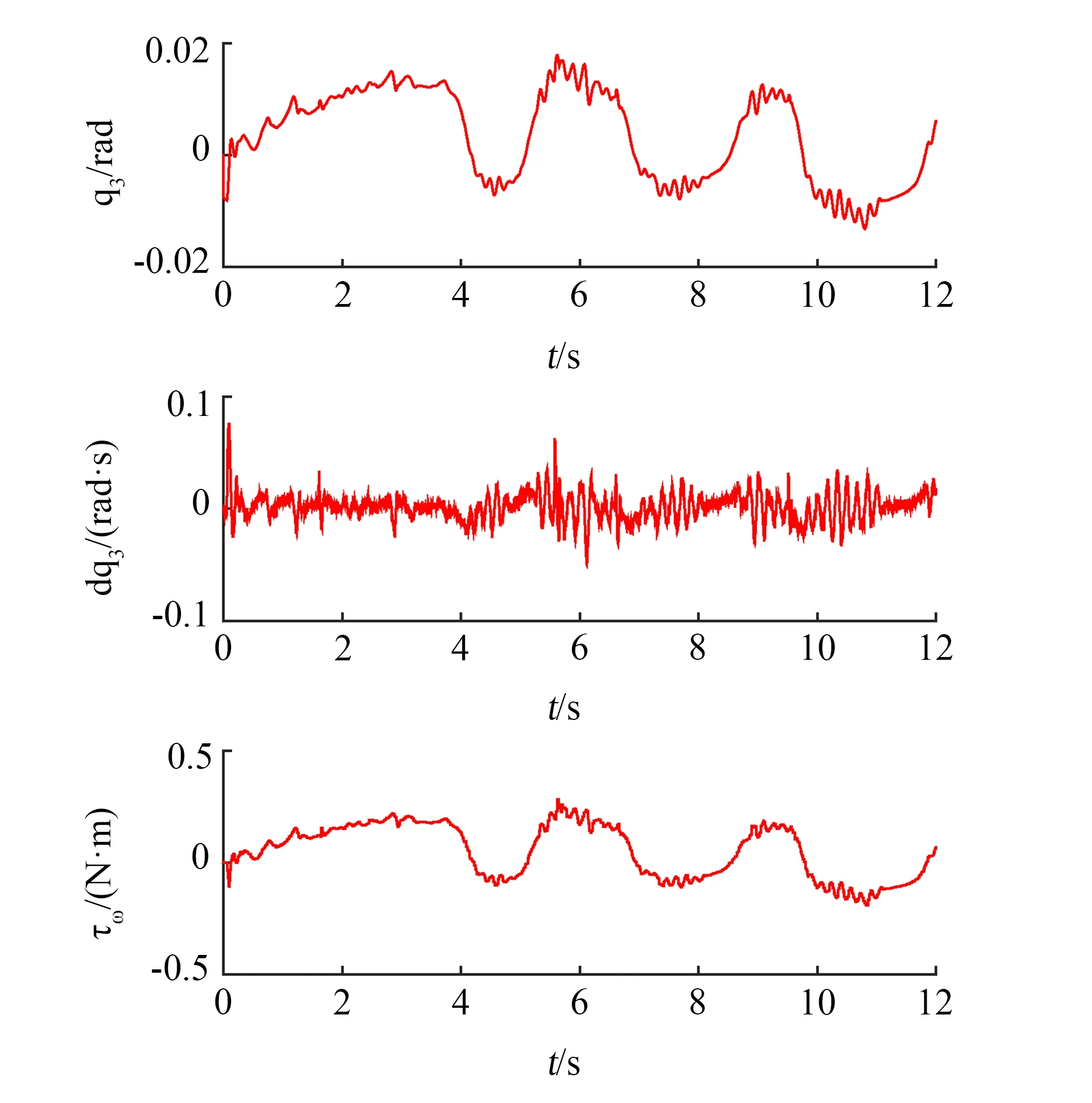
图8 原地俯仰平衡实验数据

图9 原地俯仰平衡实验视频连拍

进一步，将PMM应用于该样机摆动车把模式下行走平衡实验中[20]。仅给出实验部分视频连拍图，如图10所示，样机平衡时间在10s以上。最终，应用PMM建立的变结构两轮车机器人力学模型仅有11KiB，运行在DSP(TMS320F28335，150MiB主频)硬件平台上，平均耗时14.3μs。由于物理样机实验伺服周期为33ms，模型运行时间仅占整个伺服周期的0.04%。两者的时间差说明，PMM模型计算的极少量耗时可以为数据采集、控制器计算和数据传输等留有足够的时间裕度。故PMM所建立的动力学模型满足实时计算的要求，验证了PMM在变结构两轮车机器人系统中的有效性与可靠性。

图10 摆车把行走平衡实验视频连拍

将PMM继续推广到独轮车机器人直线行走定位控制实验[21]，机构简图与样机如图11所示。

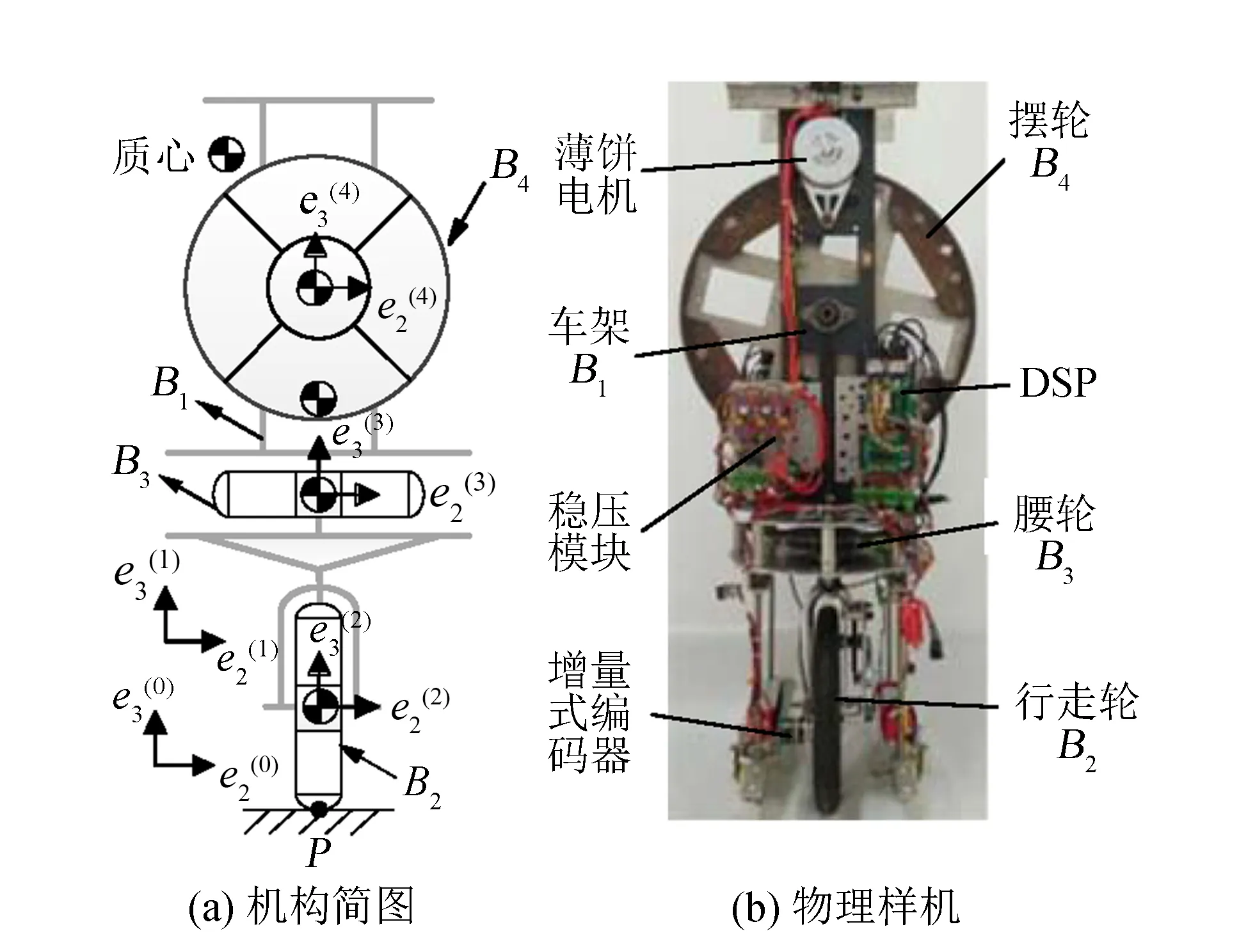
图11 独轮车机器人

图12为实验数据曲线，图13为物理样机实验视频连拍图。由图12、13可看出，独轮车机器人横滚角和俯仰角稳定在±0.05rad范围内，行走轮质心在x方向上的位移从0m运动到3m附近后，在小范围内保持稳定，期望值为3.2m，误差仅占总长的6%；行走轮质心在y方向上的位移在±0.005m范围内波动，说明车身在作直线运动，实现了独轮车机器人直线定位控制目标，验证了模型可靠性。最终，完成独轮车机器人直线定位控制实验的动力学模型仅有22KiB，运行在主频1.8GiB、双核CPU、2GiB内存、Win7操作系统和VC++环境的工控机平台上，平均耗时24.7μs。独轮车机器人物理样机实验伺服周期为44ms，模型运行时间仅占整个伺服周期的0.05%，与两轮车机器人情况类似，也可以说明PMM输出模型的计算耗时可满足物理样机实验中实时计算的需要，验证了PMM在独轮车机器人系统中的有效性。

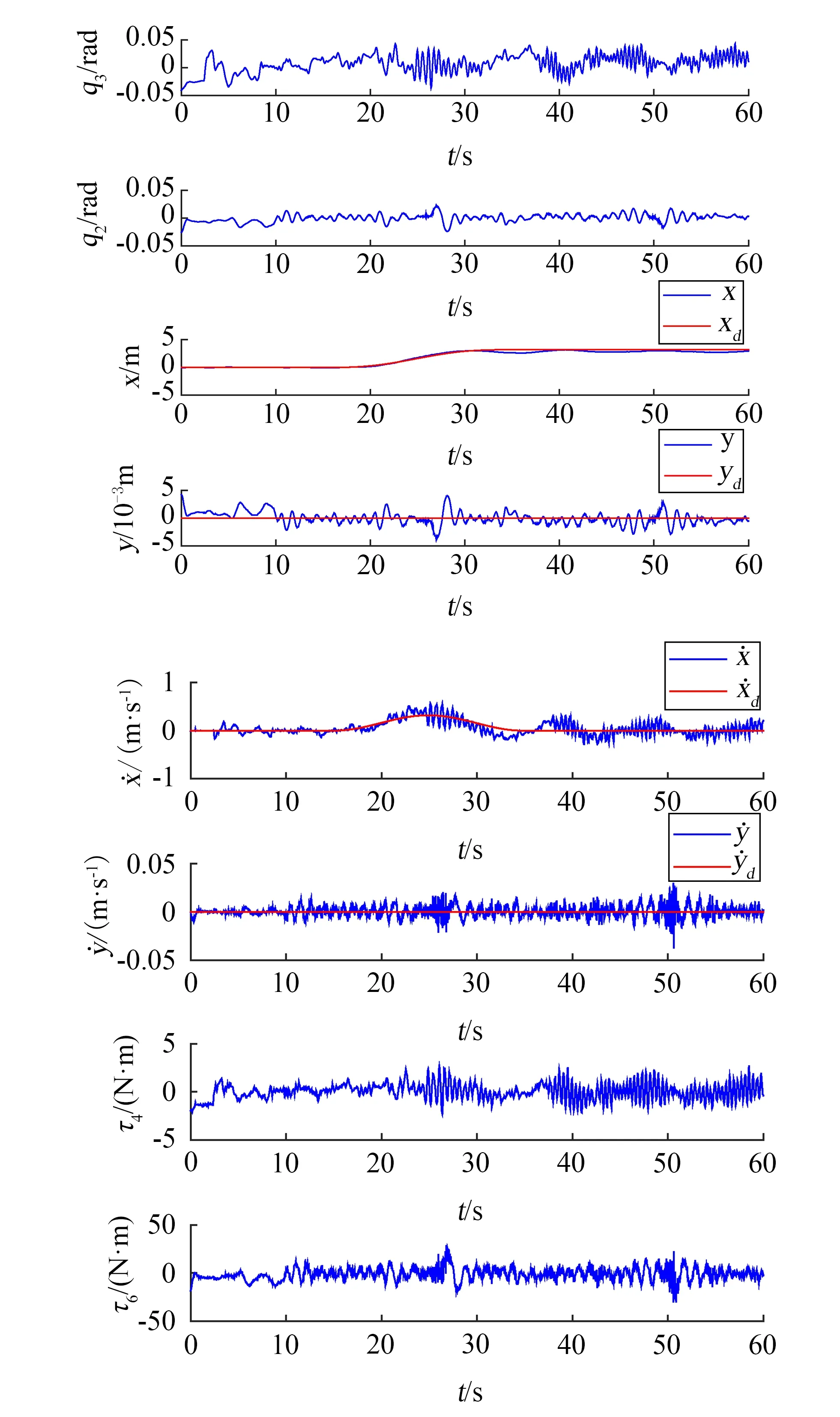
图12 独轮车机器人直线定位控制实验数据曲线

图13 直线定位实验视频连拍图

综上所述，所提方法(PMM)能够满足不同欠驱动非完整约束系统的基础实验要求，验证了有效性与可靠性，更进一步说明PMM高效和通用性强的特点。

4 结束语

1)提出一种程式化动力学建模方法(PMM)，利用该方法建立斯坦福机械臂力学模型并作仿真分析，仿真结果验证了PMM的可靠性。进一步，将PMM与常规Lagrange方法所建立的斯坦福机械臂动力学模型相比发现，PMM所建模型的复杂程度降低了67.6%，运行在主频1.8GiB、双核CPU、2GiB内存、Win7操作系统和VC++环境的工控机平台上，计算效率提高了66.3%。

2)将PMM推广到欠驱动非完整约束系统，仿真分析和物理样机实验结果表明，应用PMM所建立的动力学模型可满足不同物理样机及不同基础实验的实时计算要求，验证了PMM在欠驱动非完整约束系统的有效性，进一步阐明了PMM通用性强、适用范围广的特点。

3)PMM所表现出的高效、便捷及通用性强等特点，为机器人领域建立动力学模型所用方法提供一种选择，具有较强的指导意义和参考价值。