无人机载PolInSAR城区散射机制初步分析
吕泽鑫, 仇晓兰, 丁赤飚
(1. 中国科学院空间信息处理与应用系统技术重点实验室, 北京 100190;2. 苏州市空天大数据智能应用技术重点实验室, 江苏苏州 215124; 3. 苏州空天信息研究院, 江苏苏州 215124;4. 中国科学院空天信息创新研究院, 北京 100190; 5. 中国科学院大学电子电气与通信工程学院, 北京 100049)
0 引言
建筑是城区的主要目标,通过遥感手段提取建筑的结构和高度有助于城区规划和自然灾害评估。传统光学遥感手段受限于天气,但合成孔径雷达(SAR)能够在全天时全天候的条件下工作。此外,相较于传统平台,我们还可以将SAR安装在无人机上,从而可以更方便地获取数据。
干涉SAR和 极化干涉SAR经常被用于反演目标参数,但它们很难解释目标的散射机理。目前,已经有很多研究人员尝试对目标的散射机理进行解释。Frank分析了Pauli分解的相位中心和建筑高度的关系。李宁等分析了高分辨率极化SAR图像中建筑的散射特性。 然而,他们没有解释极化干涉SAR的物理意义。
因此,我们通过使用Ku波段无人机载极化干涉SAR数据,尝试对极化干涉SAR的散射机理进行解释。我们获得了不同目标下极化干涉SAR最接近的散射机制,以及极化干涉和Pauli分解的相位中心关系。为了保证结论的可靠性,我们使用C波段机载极化干涉SAR数据进行验证,机载得到的结论与无人机得到的一致。
1 模 型
1.1 干涉SAR
干涉SAR 通过同一区域不同入射角的两幅图像来获取干涉相位。我们通常用两种方式获取图像,包括使用双天线飞机进行单次飞行和单天线飞机重轨飞行。

Δ=-=cos(-)
(1)
式中,为干涉相位,为波长,和为天线与目标间的距离,为基线长度,为入射角,为基线角。如果系统是一发双收,则=1,若是双发双收,则=2。
然后,我们可以根据天线和目标的几何位置关系反演目标高度。
=-sin
(2)
式中,为目标高度,为平台高度。
目标高度与基线和基线角的敏感度如公式(3)和(4)所示。
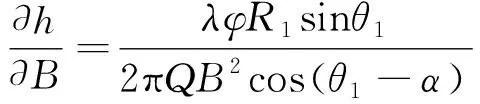
(3)
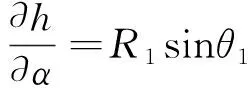
(4)
1.2 极化干涉SAR
相较于干涉SAR,极化干涉SAR可以提高图像的相干性。它结合了4种极化方式,并采用散射向量的方式表达。散射向量如下所示:
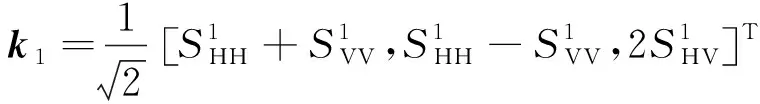

(5)
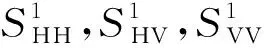
通过最大化相干系数,我们可以通过文献[8]中的办法得到三组权重。


(6)
其中,对应特征值最大的一组权重得到的极化干涉向量,被用于构建极化干涉最优分解。表达式如下:

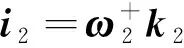
(7)
式中,和是两组权重,和是极化干涉最优分解得到的向量。
2 数 据
为了分析不同极化方式间的差异并确保结论的可靠性,我们使用了两个SAR系统,包括Ku波段无人机载极化干涉SAR系统和C波段机载极化干涉SAR系统。我们用无人机载系统分析结果,用机载系统对结论进行验证。
无人机载极化干涉SAR系统是由中国科学院空天信息创新研究院和中科宇达公司于2020年共同研制的。系统工作于Ku波段,相关的系统参数已在表1中列出。该系统如图 1所示。我们使用的数据位于中国上海复旦大学,该区域主要包括不同种类的建筑、树木和一个体育场。建筑高度大约15 m,楼顶的形状为三角形或凹凸不平。道路两旁种有梧桐树,树高约10~20 m。

图1 无人机载极化干涉SAR系统
机载极化干涉SAR系统是由中国科学院空天信息创新研究院研制,工作于C波段。相关参数在表1中列出。我们使用的数据位于中国甘肃省敦煌市,该区域包含的地物种类丰富,主要有林地、建筑、河流、山地等。

表1 极化干涉SAR系统参数
反演目标高度的步骤如下:
1) 通过对SAR回波使用-成像算法和自聚焦算法来获取SAR图像。
2) 对获取的两幅图像配准,并得到干涉相位。
3) 对SAR图像中相干性高的像素进行掩膜处理。记录掩膜后散射值较大的像素的位置。
4) 对步骤2)获取的图像,进行去平地。之后我们不需要进行相位解缠,因为目标高度小于干涉SAR的不模糊高度。
5) 使用Goldstein算法对图像进行滤波。
6) 反演目标高度。只保留掩膜后对应像素的高度,将其他像素的高度置零。
3 结 果
3.1 无人机载极化干涉SAR系统结果
无人机载系统使用的数据如图2所示。通过对极化干涉最优分解得到的变量计算干涉相位,我们可以根据公式(2)反演目标的高度,反演结果如图3所示。此外,我们还可以获取不同极化方式下的目标高度,不同极化方式包括HH、HV、VH、VV和3种Pauli分解。

(a) 无人机载SAR图像 (b) 谷歌地球光学图像 图2 无人机载极化干涉SAR系统成像区域
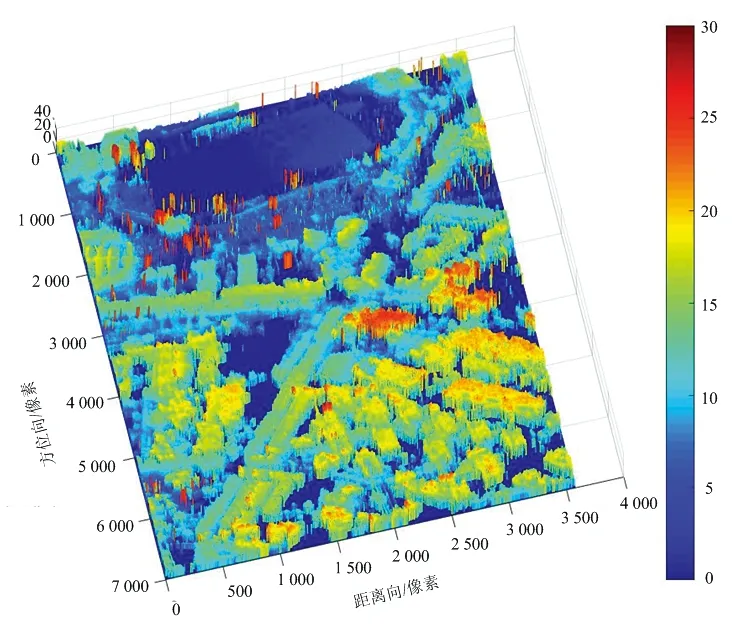
图3 无人机载SAR系统通过极化干涉最优分解反演的高度图
为了分析不同极化方式下的高度差异,我们选取了几个典型区域。区域1是一个体育场里的照明灯,高度大约30 m。区域2和区域3都是房顶形状凹凸不平的教学楼。区域4是房顶形状为三角形的居民楼。
接着我们分别得到了使用极化干涉和Pauli分解反演出的高度结果,并计算了不同目标下两种方法的高度差,结果如图4所示。

图4 Ku波段无人机载系统中极化干涉和Pauli分解的高度差异
这里我们需要解释一下,当干涉相位差比较小的时候,两种方法的高度差对基线和基线角不敏感。因此,即使基线存在较小的误差,我们的结果仍然是稳定的。
在图4中,每一行为同一个目标的结果。第一列是极化干涉反演的高度,第二列是对应的光学图,第3到第5列是极化干涉最优分解与Pauli分解的高度差,对应的Pauli分解分别是单次散射、0°二面角的二次散射和45°二面角的二次散射。
然后,我们可以计算各个区域的高度差并进行分析。选择的区域已画在图2中的红色框中,计算的高度差如表2所示。

表2 Ku波段无人机载SAR系统不同极化模式的高度差异
在表2中,表示极化干涉最优分解反演的高度,,,分别表示单次散射、0°二面角的二次散射和45°二面角的二次散射反演的高度。“均值”表示该区域高度差的均值,“标准差”表示该区域高度差的标准差。标红的值表示每行中最小的均值。
对于照明灯和房顶为凹凸不平的建筑,极化干涉最优分解的相位中心更接近于单次散射。对于屋顶为三角形的建筑,极化干涉最优分解的相位中心接近于45°二面角的二次散射。此外,区域1的高度差比其他区域的更小。区域1的照明灯大约有30 m,其他区域的建筑大约20 m。
因此,我们可以得出结论,当目标比较高时,极化干涉最优分解的相位中心高度比Pauli分解的更低,并且它们的高度差异比其他区域的要更小。这种情况下,极化干涉的相位中心非常接近Pauli分解。
3.2 机载极化干涉SAR系统结果
为了证明极化干涉与Pauli分解的高度差异,是由目标特性而非系统误差引起的,我们还使用了另一个机载极化干涉SAR系统的数据进行验证。该数据的SAR图像与光学图像如图5所示,极化干涉最优分解反演的高度如图6所示。

(a) 机载SAR图像 (b) 谷歌地球光学图像图5 C波段机载极化干涉SAR系统成像区域

图6 机载SAR系统通过极化干涉最优分解反演的高度图
我们同样选取两个区域进行验证。区域1是一幢6层的居民楼,房顶为三角形,这与复旦数据区域4的建筑类型一致。区域2是一幢10层的建筑,房顶是凹凸不平的,这与复旦数据区域2和区域3的建筑类型一致。对应区域使用两种方法得到的高度差异如图7所示,相应的高度差同样列在表3中。
表3中标红的值表示每行中最小的均值。

表3 C波段机载SAR系统不同极化模式的高度差异
对于三角形房顶的建筑,极化干涉最优分解的相位中心接近45°二面角的二次散射。对于房顶凹凸不平的建筑,极化干涉最优分解的相位中心接近单次散射。这两个结论与复旦数据得到的结论一致。此外,对于区域2的高层建筑,极化干涉最优分解的相位中心高度仍然比Pauli分解的相位中心低,并且他们的距离比其他区域的小。这个结论也与复旦数据区域1照明灯得到的结论一致。因此,机载极化干涉SAR系统的结果可以证明本文通过无人机系统获取的结论是稳定的,并且该结论可以应用于其他机载系统。

图7 C波段机载系统中极化干涉和Pauli分解的高度差异
4 结束语
本文通过使用无人机载数据,比较了极化干涉SAR与Pauli分解反演的高度差异,进而获取极化干涉SAR作用在不同目标下最接近的散射机制。此外,我们使用了机载极化干涉SAR数据来证明两种极化方式的高度差异是由目标特性而非系统误差导致的。因此,我们得到的结论是稳定的,并且可以被用于不同机载极化干涉SAR系统。

