自转多方球的内部结构
罗昕睿,余 聪
(中山大学 物理与天文学院,广东 珠海 519082)
多方球经常被作为模型来描述气状恒星的内部结构. 对于静止的多方球,利用流体静力学平衡方程以及多方关系可以得到莱恩-埃姆登方程,通过求解该方程可以近似描述恒星的内部结构. 但在更一般的情况下,恒星处于自转中,因此旋转对恒星多方球模型的外边界与内部结构的影响尤为重要.而当考虑旋转后,就需要对莱恩-埃姆登方程进行修改,修改后的方程从一维的常微分方程变成二维的偏微分方程.当自转速度较慢时,此时的自转多方球可以看成是对静止多方球的一个偏移,所以可以利用微扰展开的方法进行求解,进而对自转较慢的多方球的外边界及内部结构有一个较为精准的认识.
1 自转情形下对莱登-埃姆登方程的修改
在多方球模型中,假设压强和密度满足下列关系:
(1)
其中,p为内部压强,ρ为内部密度,K为常数,n为多方指数.这个关系给出了气状恒星内部的压强是如何随着内部密度的改变而改变的,并由此结合一些基本动力学方程与热力学方程就可以计算出恒星的内部密度分布、内部质量分布、内部温度分布、熵轮廓等基本性质,进而使我们对恒星内部结构有一个直观的认识.尽管这个关系是假设的,但利用该关系计算出来的结果与一些恒星的标准模型作比较却非常接近,因此这个假设是非常合理的[8].下面我们主要利用流体静力学平衡方程,分别讨论静止情形下的多方球满足的方程与考虑自转后的多方球满足的方程.
对于静止多方球内部达到流体静力学平衡后,会满足下列方程:
∇p=ρ∇V
(2)
∇2V=-4πGρ
(3)
其中,式(3)是引力势能V满足的泊松方程.对径向长度r和密度ρ进行无量纲处理,并代入上述式(2)、(3),得到
(4)
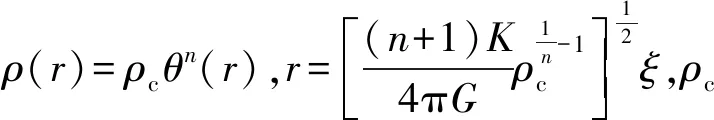
考虑自转后,假设自转方向是沿着直角坐标下的z轴方向,则多方球的流体静力学平衡方程在球坐标系(r,ϑ,φ)中的表达式为
(5)
(6)
μ=cos ϑ
(7)
其中,ω为多方球的自转速度.而式(3)也可以写为
(8)
将式(5)、式(6)、式(8)结合在一起,可得
(9)
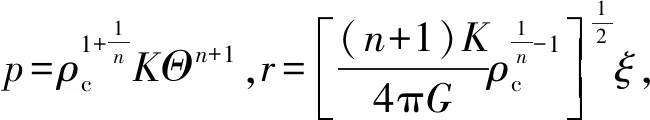
(10)
(11)
其中,ξ为无量纲化后的径向长度,ρcΘn为无量纲化后的密度,v为无量纲化后的自转速度的平方. 式(10)为自转情形下对莱恩-埃姆登方程的修改[1-3].
2 求解自转较慢情形下的方程
假设自转较慢情形下方程的解是对静止多方球的解的一个微扰[1,3],即
Θ(ξ,μ)=θ(ξ)+vΨ(ξ,μ)+…
(12)
其中θ(ξ)为静止情形下莱恩-埃姆登方程的解,故不依赖角度.若仅考虑v的一阶项,将式(12)代入式(10),并结合式(4)可得
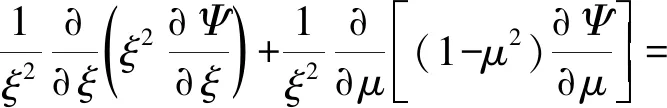
(13)
利用分离变量的思路[1,3],Ψ可以展开为
(14)
其中,ψ0、ψj都是仅依赖ξ的函数.Pj(μ)是仅依赖μ的勒让德函数,其对应的勒让德方程如下
(15)
将展开式(14)代入式(13),并利用式(15)进行化简,可得ψ0、ψj满足的方程如下
(16)
j=1,2,3,4,…
(17)
下面需要通过计算势能,进而确定解式(14)的每一项前面的系数Aj.
将式(8)(即球坐标下的泊松方程)写成无量纲化的形式,并代入假设解,得
(18)
仍然利用分离变量的思路,假设上述方程的解具有如下形式:
(19)
其中,U(ξ)是静止多方球的势能,V0、Vj是仅依赖ξ的函数,Pj(μ)是仅依赖μ的勒让德函数.将式(19)代入式(18),通过比较Pj(μ)前的系数,可得
(20)
(21)
(22)
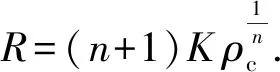
利用式(20)可得
U=Rθ+cons
(23)
利用式(16)和式(21)可得
(24)
利用式(17)和式(22)可得
(25)
进而得到式(22)的一个特解:
Vj=RAjψj+cons
(26)
但式(22)的通解还需加上下面常微分方程的解:
(27)
而式(27)的解为RBjξj,Bj为常数,故式(22)的通解为
Vj=R(Ajψj+Bjξj)+cons
(28)
综合式(23)、式(24)、式(28),可得最终解为
(29)
此时,式(29)将势能V与无量纲化后表征内部压强的Θ联系在了一起,但仍存在一个待定系数Bj,而式(5)正好是压强与势能满足的关系,可以借此确定Bj.
(30)
将式(29)代入式(30),通过比较Pj(μ)的系数,可得
Bj=0,j≠2,
(31)
进而可得
(32)
需要注意的是,式(32)表征的是多方球内部某处的势能,多方球外部的势能应由下列展开式所表征,即
(33)
而多方球内外的势能大小及势能一阶导数在多方球外边界处应保持相等,否则势能会出现不连续性.由于这里考虑的多方球自转速度较慢,多方球外边界可近似取为静止多方球的外边界,设为ξ1,则由V(ξ1)=Vext(ξ1),V′(ξ1)=V′ext(ξ1),可得
Aj=Cj=0,j≠2
而j=2,为
(34)
(35)
解得
(36)
进而得到最终解为
Θ=θ+
(37)
由式(16)、式(17)知ψ0(ξ)和ψ2(ξ)满足下列的常微分方程:
(38)
(39)
式(4)、式(38)、式(39)均为常微分方程,利用四阶显式龙格-库塔方法[6,7]可数值求解上述常微分方程.
3 求解自转多方球的外边界
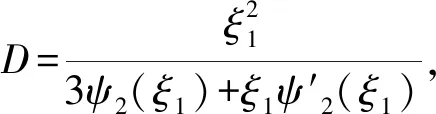
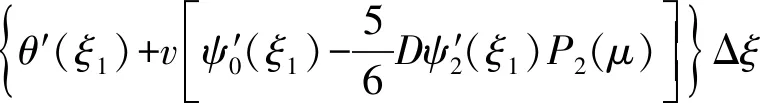
(40)
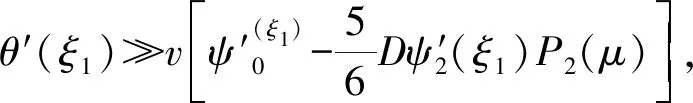
(41)
多方球内部压强越往外越小,故θ(ξ)是一个单调递减的函数,所以-θ′(ξ1)=|θ′(ξ1)|,进而得到自转情形下的多方球外边界为
(42)
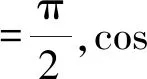
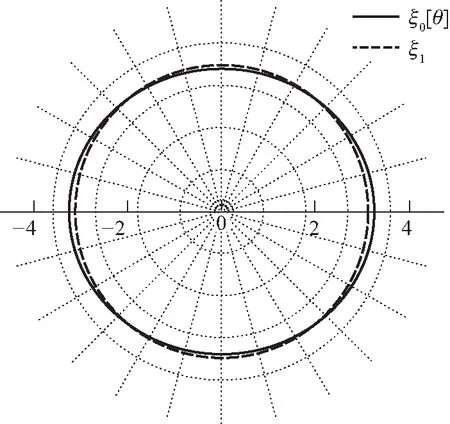
n=1,v=0.018
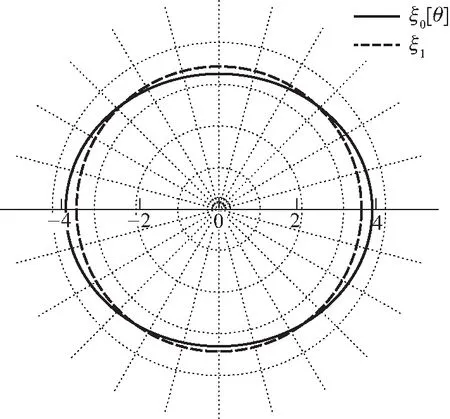
n=1.5,v=0.018
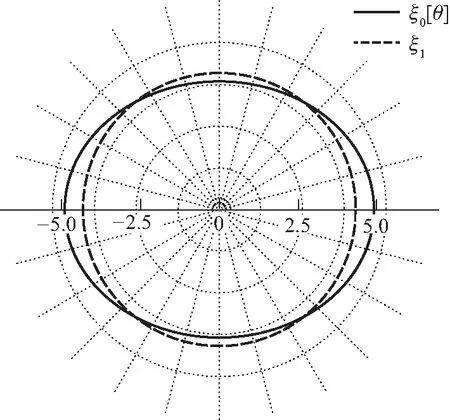
n=2,v=0.018图1 自转情形下的多方球外边界(n ≤ 2)
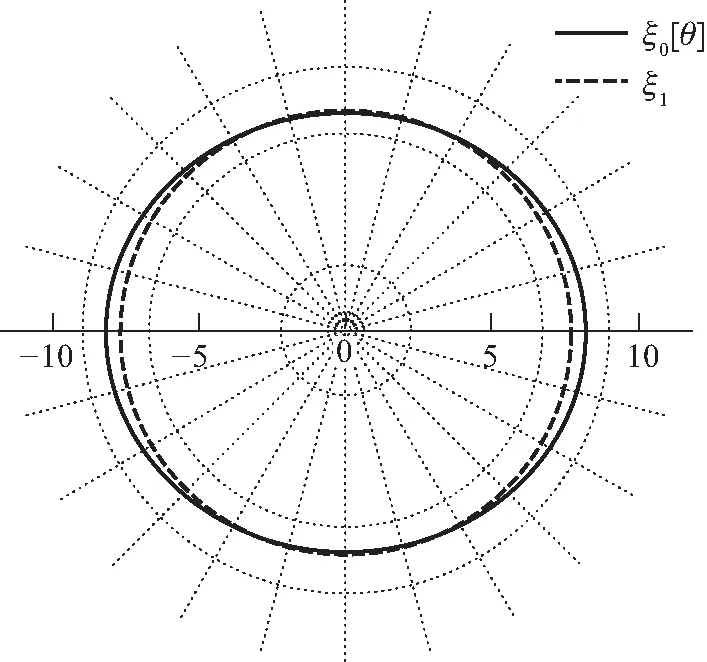
n=3,v=0.001 8
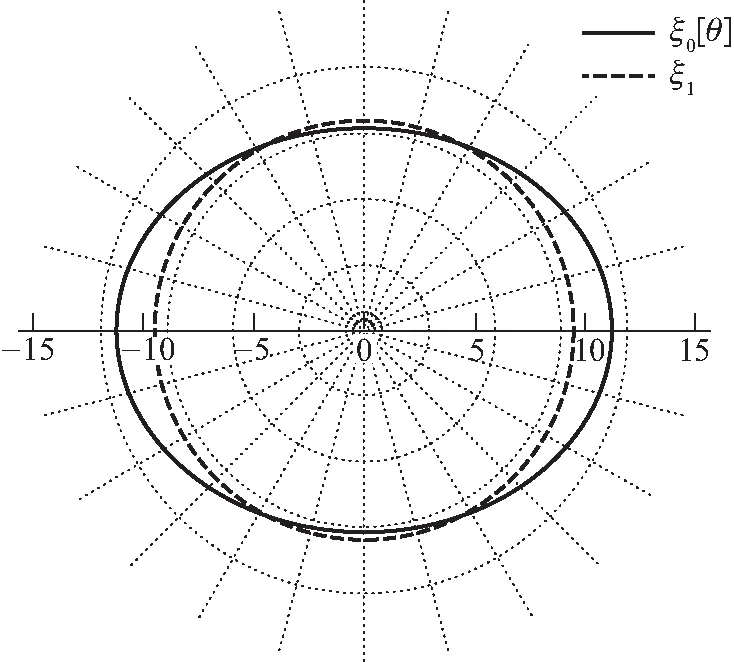
n=3.5,v=0.001 8
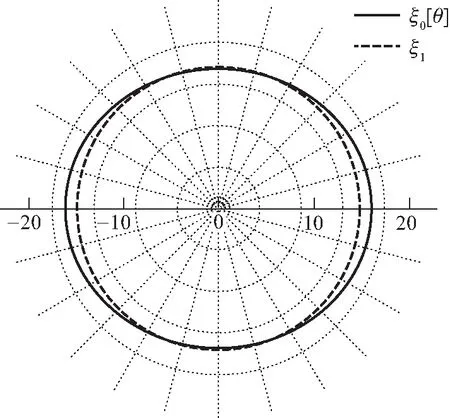
n=4,v=0.000 18图2 自转情形下的多方球外边界(3≤n≤4)
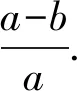
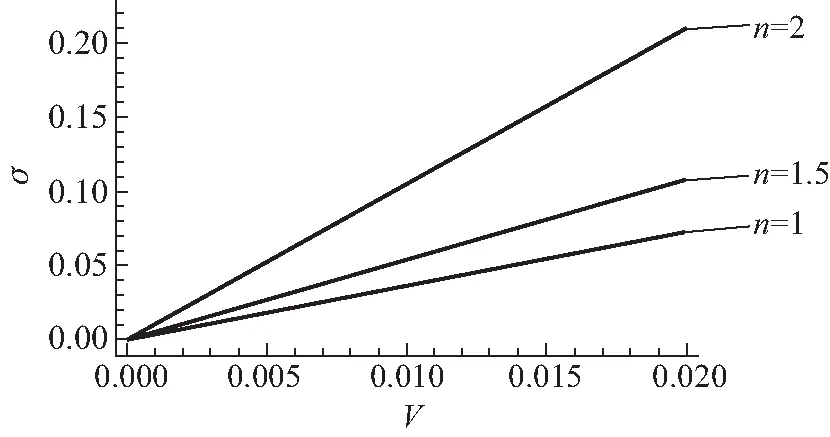
图3 自转情形下多方球扁率随无量纲化自转速度的平方的变化(n≤2)
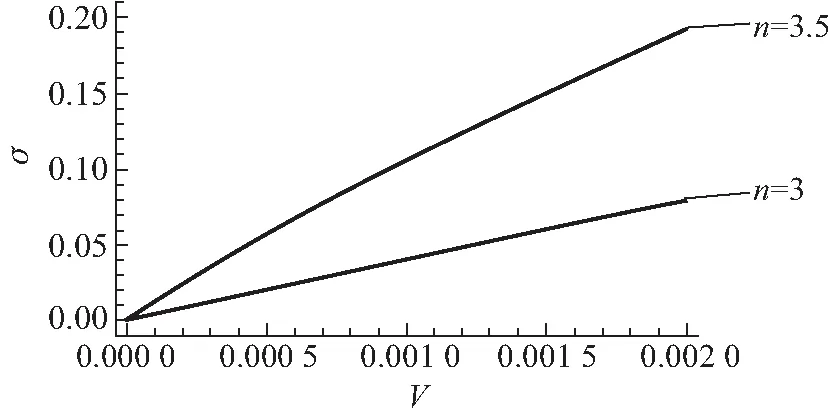
图4 自转情形下多方球扁率随无量纲化自转速度的平方的变化(3≤n≤4)
由图可见,n越大,自转情形下多方球扁率受自转速度的影响越敏感,形变越明显.可以猜测,这主要是因为,n越大,其静止多方球模型的密度分布越为集中,如图5所示,导致静止多方球的外边界附近压强较小,进而更容易受到由自转带来的离心力的影响,造成形变.
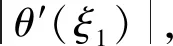
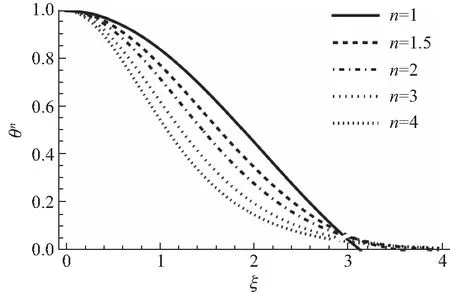
图5 不同n的静止多方球(无量纲)密度分布
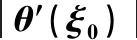
表1 不同n的静止多方球的及
4 自转情形下的多方球内部密度分布
以n=2,v=0.018为例,自转情形下的多方球沿不同角度的内部密度分布如图6、图7所示.
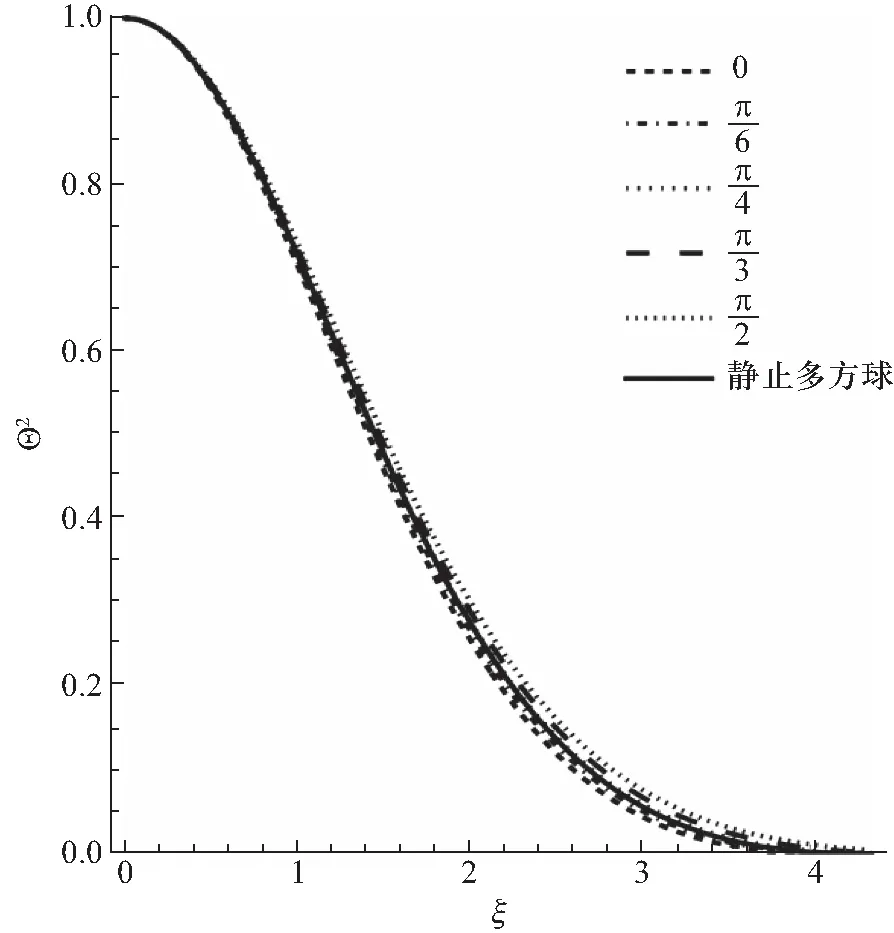
图6 自转多方球沿不同角度的内部密度分布(无量纲)
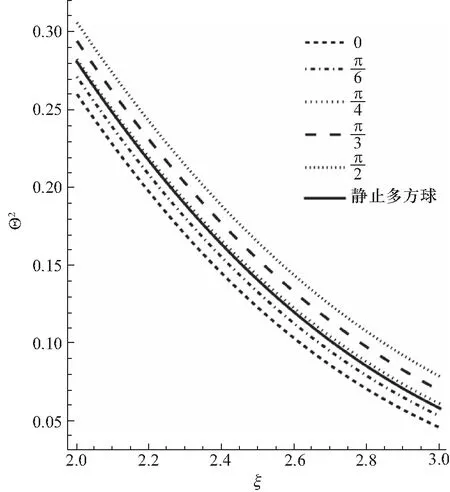
图7 对图6进行局部放大
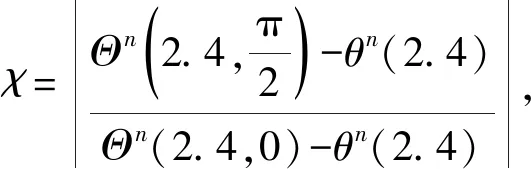
当然,不同的n对应的密度分布差异值所取的径向长度也会有所不同,仍然选取对应两极方向和赤道方向的密度差异最为明显的无量纲径向长度ξ即可.这里仅代表n=2.
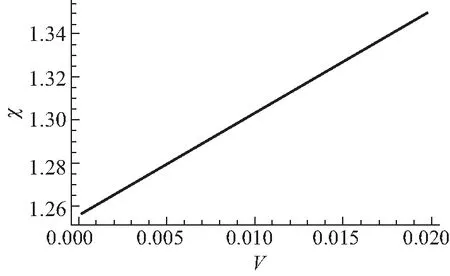
图8 密度分布差异值与(无量纲化)自转速度的平方的关系(n=2)
可以看到,随着自转速度的增加,密度分布差异值也在增加,这是符合预测的.因为自转速度越大,多方球的赤道方向上的物质受到更强的离心力,进而往外流动,并且两极处的物质也更容易“甩”到赤道附近,使得赤道方向上的密度分布越来越松散,而两极方向上的密度分布越来越集中.
5 求解自转多方球的质量半径关系
最后,我们计算自转多方球的质量半径关系,利用式(43)
M=2π∬ρr2drdμ
(43)
将无量纲化半径ξ及密度Θ代入,并保留v的一阶项,得到从中心到任意径向长度ξ′的质量公式:
(44)
其中
A=θn+nθn-1vψ0(ξ)-
(45)
(46)
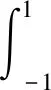
(47)
(48)
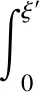
(49)
因此,质量半径关系为
(50)
对于静止多方球,即v=0时,其质量半径关系为
M0=-Gξ′2θ′(ξ′)
(51)
利用式(50)可以改写式(49)为
(52)
若将二者画出来,如图9—12所示.
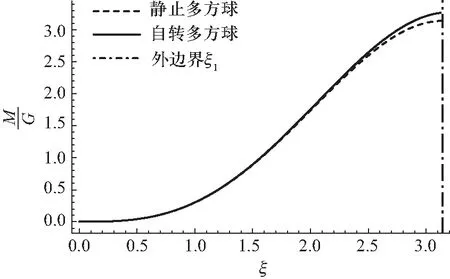
图9 多方球(无量纲化)质量半径关系(n=1,v=0.018)
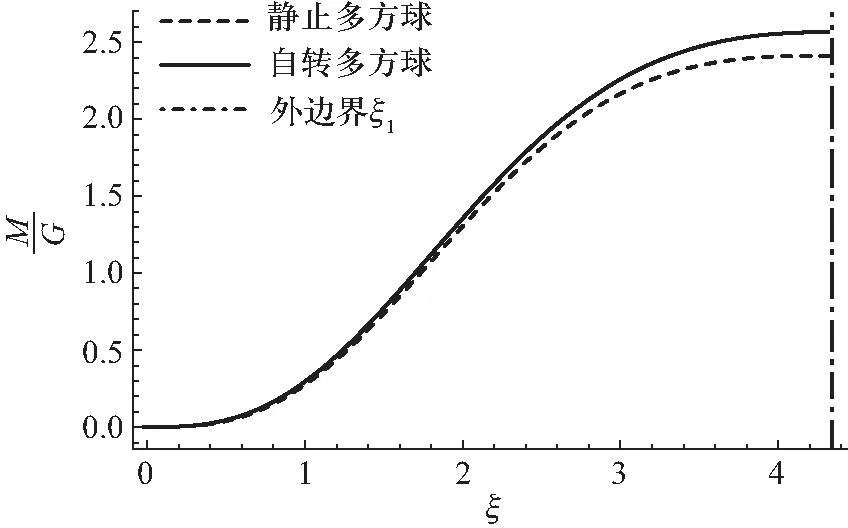
图10 多方球(无量纲化)质量半径关系(n=2,v=0.018)
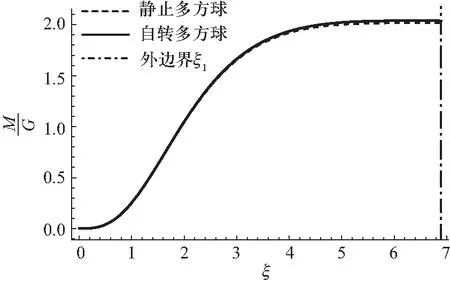
图11 多方球(无量纲化)质量半径关系(n=3,v=0.001 8)
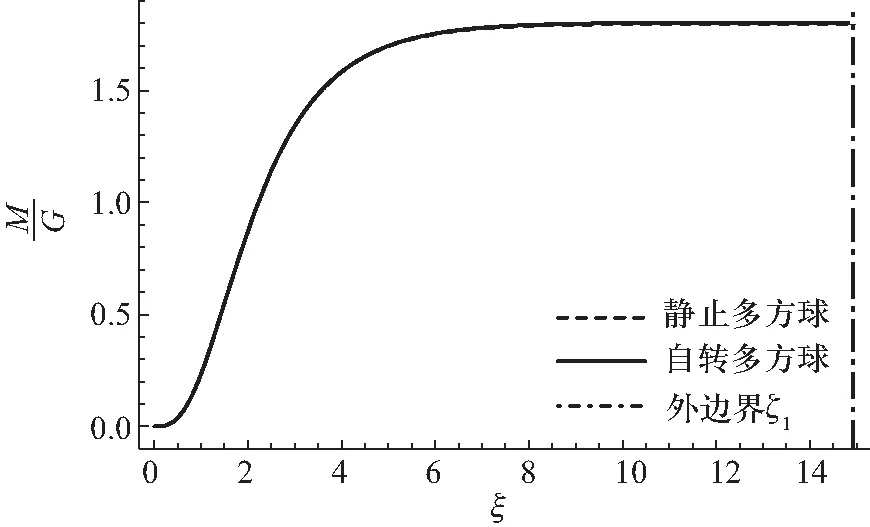
图12 多方球(无量纲化)质量半径关系(n=4,v=0.000 18)
可以看到,在相同中心密度的情况下,自转多方球的质量要大于静止多方球的质量,并且由图可以看到,半径越大,自转多方球与静止多方球的质量相差越大.这是可以被理解的,在靠近核心处,离心力的作用还较小,可以被忽略,故主要的流体静力学平衡还是引力与压强达到平衡,所以静止多方球与自转多方球的质量较为接近;而越往外,离心力的作用越来越大,当大到一定程度后,离心力的作用不可被忽略,此时向内的引力需要和向外的压强与离心力达到平衡,故需要的更大质量来提供足够的引力,所以越往外,自转多方球的质量与静止多方球的质量相差越大.
6 讨论求解方法的局限性
本文利用微扰法求解自转速度较慢的多方球时较为准确,但当自转速度较快时,微扰法将不再适用.若仍采用微扰法进行求解,求解出来的压强为0的等高线会沿赤道裂开,也就代表了微扰法求解的多方球外边界也沿赤道裂开,如图13所示.本文认为当出现这个状况时,微扰法将不再适用于求解自转多方球,应该使用其它办法进行求解.
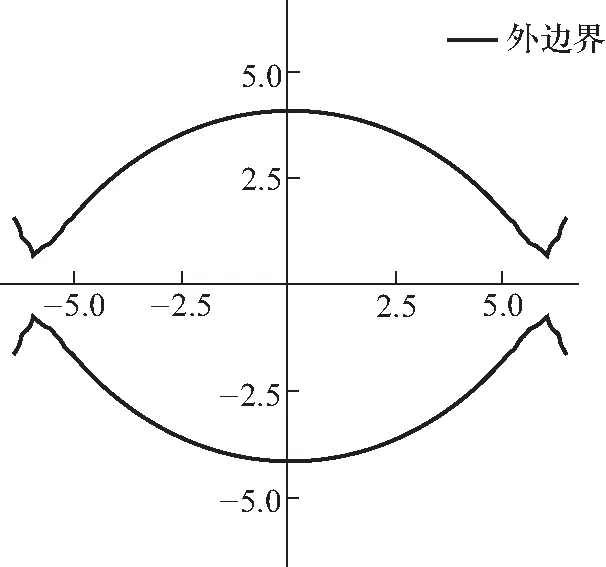
图13 利用微扰法求解的自转较快多方球外边界(n=2)
——《势能》

