坐标、动量表象的不对称积分投影算符与宇称测量
王 帅,张建东,王凤飞,朱小芹
(江苏理工学院 数理学院,江苏 常州 213001)
量子力学表象和算符是量子力学中最基本且重要的概念,它们在量子理论中起着重要的作用.特别是,有序算符内的积分技术(简称IWOP)[1]进一步推动了量子力学表象与算符的变换理论,使狄拉克符号法更完美、更具体,能更好的表达物理规律.


(1)

(2)
它也是一个厄米算符.它与式(1)是否具有类似的性质,对应于同一种物理测量呢?本文将会作进一步的探讨.
在本工作中,本文将借助IWOP技术讨论以上问题,给出不对称积分型投影算符式(1)和式(2)的积分显式,进而讨论这一类厄米算符所对应的物理测量.
1 双模坐标表象的不对称积分型投影算符
为了便于学生对量子算符的IWOP积分技术的理解,这里给出详细的推导过程. 在Fock态表象中,坐标算符的本征态|x〉可以表示为[1]
(3)
在量子力学中,双模真空投影算符的正规乘积形式如下:
(4)
式中符号::就表示玻色算符的正规乘积排序,即所有的产生算符都排列在湮没算符的左边,在符号::内产生算符和湮没算符可以任意交换位置,而不影响结果.因此,把式(3)和式(4)代入式(1)的左边,可得

(5)
由式(5)可见,产生算符都在正规乘积符号::的左边,湮没算符都在右边.因此,式(5)右边的积分已经按正规乘积排序好了,可进一步写为

(6)
由于在正规乘积符号::内,产生算符和湮没算符位置可以任意交换,是对易的,故式(6)在数学上可直接进行积分.利用数学上的积分公式:
(7)
其积分收敛条件为Re(α)>0,对式(6)积分可得
(8)
这样,本文就利用IWOP技术给出如式(1)所示不对称积分型投影算符的积分显式.

(9)
然后,把式(9)泰勒展开式中的产生算符都排列到符号::的左边,湮没算符排列到右边,再利用式(4)立即可得
(10)
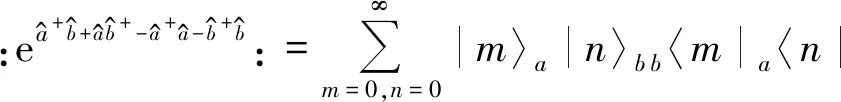
(11)
显然,与双模Fock态表象的完备性关系

另外,比较式(8)和式(11)可见,连续变量的不对称积分型投影算符和分离变量的不对称求和型投影算符是同一个厄米算符,即

(12)
自然要问,式(12)表示的不对称投影算符既然是一类厄米算符,那么它在量子力学中是否有其经典物理对应呢,即是否对应于某个物理量或某种物理测量呢? 这正是本文下面要讨论的另一个主要问题.
2 双模动量表象的不对称积分型投影算符
类似的,下面讨论基于动量表象所构造的不对称积分型投影算符.在Fock态表象中,动量算符的本征态|p〉可以表示为[1]
(13)
与式(8)的推导过程类似,可导出式(13)的积分显式为

(14)
在Fock态表象下,式(14)的右边还可以写成
(15)

(16)
虽然,式(8)与式(14)略有不同,但实质上它们都是同一类厄米算符,也都对应着同一种物理测量.下面,本文对此给出严格证明.
3 Mach-Zehnder干涉仪的宇称测量方案
在量子度量学中,基于光学Mach-Zehnder干涉仪的相位估计方案有着重要且广泛的应用[6]. 宇称测量,或称为光子数的奇偶测量,是Mach-Zehnder干涉仪相位估计方案中的一种具体的测量方法[7],如图 1所示. 在图1中,虚线框前的部分为量子态经过第一块平衡分束器BS1后,再经过相移器,这一过程通常称为参数化过程. 参数化后的量子态,本文用|Ψ〉ab来表示.这里相移器描述光经过干涉仪的两条光路所产生的相位差φ,这正是需要测量的参数.从测量的角度来讲,在量子态|Ψ〉ab之后的部分均可认为是测量部分.所以图1虚线框所示的就是Mach-Zehnder干涉仪的宇称测量方案.
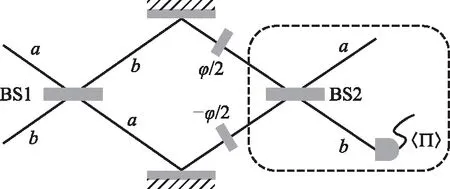
图1 Mach-Zehnder干涉仪中宇称测量方案
Mach-Zehnder干涉仪的宇称测量方案是指量子态|Ψ〉ab经过最后一块分束器后的光子数奇偶测量,即求测量算符的期望值:
(17)

(18)
(19)
在分束器的相位角θ=π/2和φ=0的特殊情况下,即考虑一块平衡分束器,高洋等人把Mach-Zehnder干涉仪的宇称测量方案表示成如下投影算符[3]:
(20)
进而简化了宇称测量信号的计算. 但他们并没有给出解析的证明.
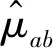
(21)
解析证明了结果式(20)的正确性,而且还给出了该测量方案在相干态表象、纠缠态表象中的表示,做了进一步推广.当θ=π/2时,即为平衡分束器时,上式简化为
(22)
显然,当式(22)中参数φ=0和φ=π时,式(22)就分别等于式(8)和式(14)了.所以,式(8)和式(14)所表示的不对称积分投影算符,都对应于任意双模量子态经过一块平衡分束器后的宇称测量方案.因此,这里就回答了本文所提出的第2个有趣问题.
另一方面,与式(11)推导类似,容易给出式(22)在Fock态表象下的表示,即

(23)
当式(23)中参数φ=0和φ=π时,式(23)就分别等于式(11)和式(15)了. 由以上讨论可见,对于同一个厄米算符,可以根据不同需要,把它表示成不同量子力学表象下的不对称投影算符形式,从而简化相关量子算符的运算.
综上所述,本文基于坐标、动量表象构造了一类简单有趣的不对称积分型投影算符,它们是量子力学上的一种厄米算符. 通过有序算符内的积分技术,得到了该类不对称积分型投影算符的正规乘积形式. 同时,本文严格证明了这类不对称投影算符对应于光学Mach-Zehnder干涉仪相位估计中的宇称测量方案,从另一个角度展现了量子力学中的厄米算符和量子表象之间的紧密关系. 本文内容比较新颖且有趣、计算推导过程相对简单易懂,为量子力学中表象变换论和狄拉克符号法提供了一个教学研究范例.

