刚性球体在转动环形凹槽内的动力学行为

雷家睿，韩润泽，王柯人，黄 敏，赵芸赫，马宇翰

(1. 北京师范大学 物理学系，北京 100875；2. 四川省成都市新都一中 铭章学院，四川 成都 610500；3. 首都师范大学附属中学，北京 100048；4. 中国工程物理研究院研究生院，北京 100193)

本文探究的问题源于国际青年物理学家锦标赛(IYPT)2021的课题之一：一个带槽的圆环形轨道围绕它垂直于地面的直径旋转，一个刚性小球可以在圆环内侧的凹槽中滚动(如图1所示).

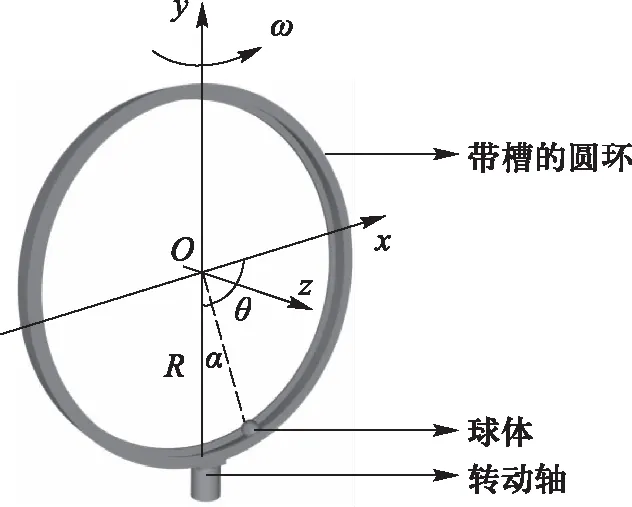
图1 装置示意图

这是一个典型的非惯性系中的刚体动力学问题，相关体系已吸引了不少研究兴趣. 例如，王永志应用势能曲线得到了此系统中球的平衡点及其性质，并对球的动力学过程进行了定性分析[1]. Burov研究了球体在绕竖直轴旋转圆环中的平衡位置，并在将其视作质点的情况下，讨论了平衡点的稳定性及摩擦力对平衡态的影响[2]. Duta和Ray在无摩擦、无自转的理想状态下，利用分析力学给出了球在绕轴旋转圆环中运动的解析解，分析了球的运动模式[3]. 此外，还有针对球在旋转抛物面[4]、旋转杆[5]上运动的研究. 然而，同时考虑球的自转和摩擦对其在非惯性系中动力学行为的影响，还未有报道.

本文基于牛顿运动方程，考虑球与轨道间的摩擦力及球的自转，使用Matlab求解了运动方程,得到了小球运动规律对相关参数的依赖. 进而搭建实验装置，在测量圆环内槽与球间摩擦系数的基础上，定量检验了理论结果.

1 理论分析

1.1 刚性小球平衡状态的分析

设大环半径为R，刚性小球半径为r，圆环绕竖直轴转动的角速度为ω，如图1所示.

在圆环的随动系中，小球在平衡时受到的科里奥利力为零，故其与槽的侧面无正压力. 若刚性小球在平衡时受到圆环底面摩擦力作用，考虑球自身的体积而非将其视作质点，摩擦力力矩将使球旋转并脱离稳定状态，这与球处于平衡状态的前提相悖. 因此，刚性小球在平衡状态下不受到摩擦力作用，只受到重力和环底面支持力作用，由牛顿第二定律可知

mgtanα=mω2(R-r)sinα

(1)

解得α=0或

(2)

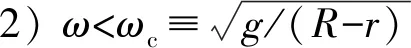
由图2可得，平衡位置α与圆环转速ω成正相关，当ω趋于无穷时，α趋于90°(图2中虚线). 另外，α与圆环半径也成正相关. 与前面分析一致，对于特定半径R，都有一个出现除α=0点以外的其他平衡位置的临界角速度，环半径越大，此临界角速度值越小.

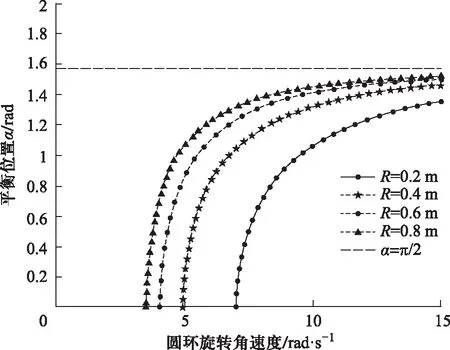
图2 平衡位置的角度随圆环角速度的变化(参数：r=0.8 cm)

1.2 刚性小球运动的动力学过程

在理解了小球可能存在的静态平衡后，本节将研究小球的运动特征. 为了简化理论分析，现做出如下限定：球与槽的相对位置如图3所示，即槽的截面为方形，球与槽的侧面和底面分别相切. 这限定了球的质心不会有如图3中左右的位移，只有垂直于纸面方向的位移，且槽侧面对球的支持力在水平方向(z轴)上.

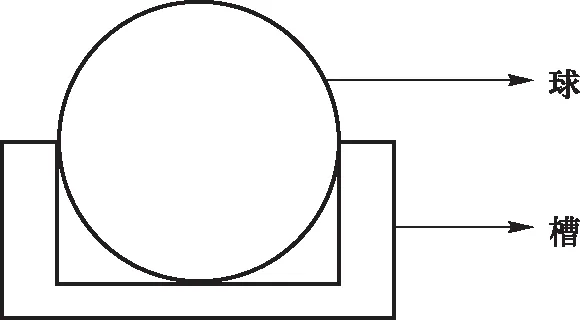
图3 球与槽的相对关系

取x轴为极轴，逆时针为正方向，沿大圆环径向向外的方向矢量为er，沿大圆环切向的方向矢量为eθ，z的方向矢量为k，满足右手螺旋关系，如图4所示.

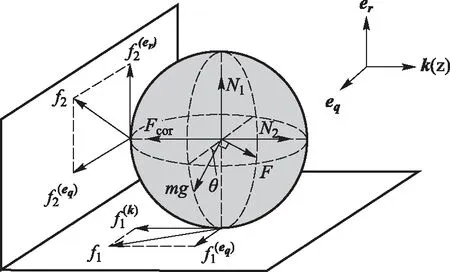
图4 小球的三维受力图及坐标系示意图

设圆环转动角速度为ω，圆环的圆心到圆环底面的距离为R，刚性小球质量为m，半径为r，重力加速度为g. 对刚性小球的三维受力分析如图4所示，其中小球位于圆环上图1中所示的位置.

设球与槽底面的正压力为N1. 在随圆环转动的非惯性系中，存在沿x轴方向的惯性离心力F与沿k方向的科里奥利力Fcor，而Fcor的存在会使得球与槽的侧壁产生与Fcor大小相同但方向相反的正压力N2；因此，圆环的槽与球之间存在两个摩擦力，分别是槽底面、侧面与球的摩擦力，它们的大小分别为：

f1=μN1

(3)

f2=μN2=μFcor

(4)

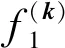
(5)

(6)

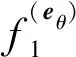
由于f1、f2方向总与接触点相对滑动方向相反，f1与f2各自的两个分力具有如下关系：

(7)

(8)

分别列出er、eθ、k方向上球运动的动力学方程为

(9)

(10)

(11)

其中

(12)

F=mω2(R-r)sinθ

(13)

对于球自转，分解到er、eθ、k方向，列出方程：

(14)

(15)

(16)

其中球的转动惯量I=2mr2/5. 在球的运动过程中，摩擦力的方向是在动态变化的，故在上述方程组中引入符号函数：

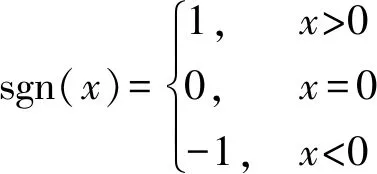
(17)

联立式(5)至式(17)，即可得到描述小球运动的二阶非线性微分方程组. 该微分方程组可使用Matlab进行其数值求解，相应结果将在2.3节中与实验结果对比时具体给出.

2 实验验证

2.1 实验装置

本文搭建的实验装置如图5所示，其中圆环由普菲德5RK60RGN-CF型60 W电机带动实现转动，电机上加装了普菲德5GU-20-K型减速齿轮降低电机的转速，使转速达到实验要求的范围. 同时，使用调速器对减速电机供电并实现电机的可控调速. 为加工得到合适的圆环，使用Shapr3D软件对圆环进行建模，并使用普通白色树脂3D打印. 使用DHTC-1型多功能微秒计连接光电门，测量圆环的转动角速度，同时监测圆环是否匀速转动.

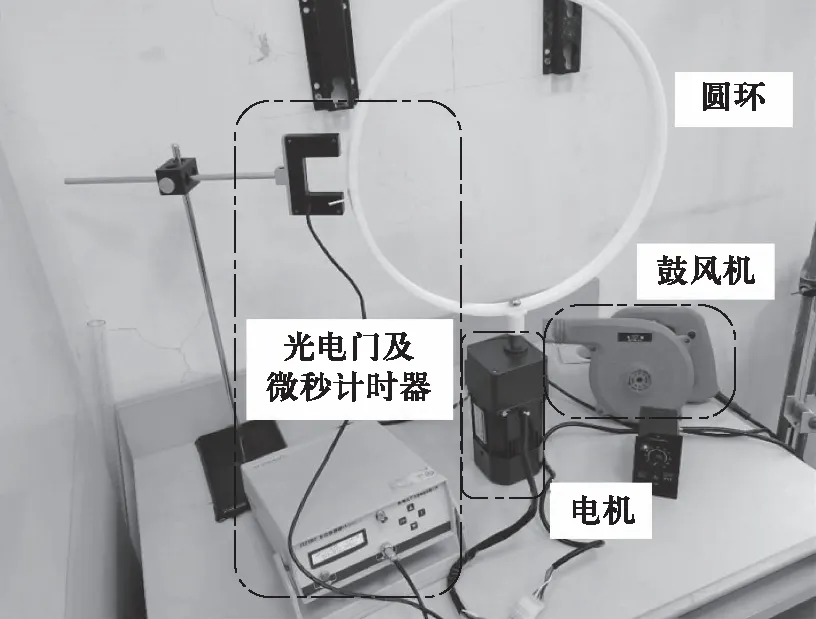
图5 实验装置图

实验中，由于刚性小球可能一直停在α=0的平衡位置而不在圆环上运动，可使用鼓风机对刚性小球提供微扰，使其能够稍偏离平衡位置并在圆环上运动. 小球的运动状态由在装置的侧面的云台搭载摄像机进行拍摄，拍摄帧率为120 fps到960 fps不等，具体帧率由圆环的转速决定. 实验后，将拍摄的视频导入Tracker，进行数据分析.

2.2 圆环与球摩擦系数的测量

在使用实验数据对理论进行验证时，需要将实验参数代入到理论方程中，进而求得理论曲线. 球半径、圆环转速等参数可以使用游标卡尺、光电门等设备直接测量得到，但球与环间的摩擦系数无法直接测量. 以下提出一种用于测量小球与圆环内壁摩擦系数的方法：

保持圆环静止不旋转，若在小角度α0时将小球释放，小球因受到摩擦力作用而做振幅衰减的阻尼振动. 对于从α0静止释放到第n次运动到振幅最大点αn的过程，由能量守恒定律可得

mg(R-r)(cosαn-cosα0)=

(18)

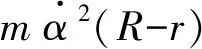
(19)

实验中，测量出α0和αi即可得到摩擦系数μ. 在圆环静止不动时，将小球小角度释放，使用Tracker软件分析得到小球第i次运动到振幅最大点时的角度αi，如图6所示.

图6 第i个振幅极大值点的角度αi实验测量值

重复多次实验，将实验数据代入式(19)可求得球与环之间的摩擦系数μ=0.048.

2.3 实验结果及理论验证

首先分别在R=0.1 m和R=0.15 m的圆环上进行实验，检验小球平衡位置和转速的关系[式(2)]，实验数据与理论对比如图7所示. 其中误差棒代表五次独立重复实验的均方差.

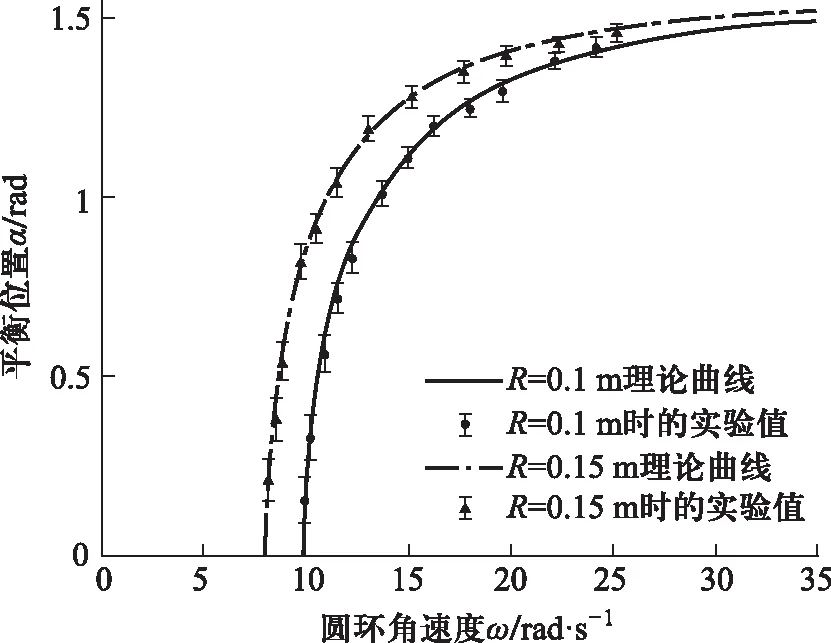
图7 r=0.016 m,R=0.10 m和0.15 m时平衡位置随角速度变化图

从图7可以看出，平衡位置与转速、圆环半径均成正相关，理论值均在实验值误差棒范围内，说明理论与实验符合良好. 同时，除了图中所示的平衡位置外，α=0对于任意转速ω均是一个平衡位置，这在实验和理论上均得到了证实.

对于球在圆环上的运动过程，需要将实验中测量得到的摩擦系数、圆环半径以及小球的初始位置和速度等参数代入到1.2节给出的动力学方程组中，求出微分方程的数值解. 再将对应的实验数据与理论值比较. 在R=0.20 m,r=0.016 m，ω分别16.20 rad/s、12.05 rad/s时，实验与理论对比如图8所示.

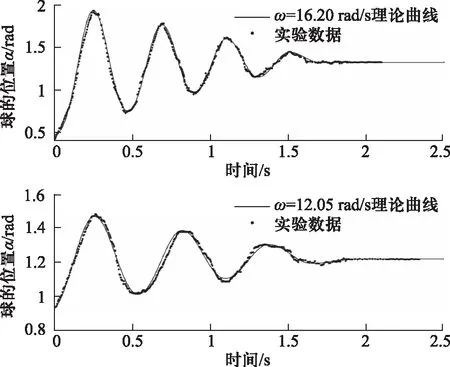
图8 R=0.20 m,ω=16.20 rad/s和ω=12.05 rad/s时理论验证

其中黑色实线为理论的数值解，黑色散点则为在实验中测得的数据点.两组独立实验数据与理论曲线均符合良好，验证了理论模型的正确性. 在对小球运动过程的理论进行验证时，摩擦系数是实验中唯一不确定的参量，它测量的精确性直接影响到了实验对理论的验证效果. 图8中的理论与实验的良好一致性，也说明了2.2节中提出的摩擦系数测量方法具有很高的精确度.

3 总结与展望

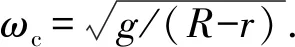
本文的研究对理解非惯性系中运动物体的旋转和摩擦对其动力学行为的影响有启发性，提出的测量弧面上物体摩擦系数的办法也具有可拓展性，可用于其它相似的系统.