两种不确定性来源对干旱指数SPEI 及干旱评估的影响

韩孺村， 张 莹,2， 李占玲

（1.中国地质大学（北京）水资源与环境学院，北京 100083；2.寿光市水利局，山东 寿光 262700）

气候变暖是人类面临的最为严重的全球环境问题，引起了世界各国政府和公众的广泛关注［1］。全球变暖背景下，干旱问题已成为生态学、气象学和水文学领域关注的重点问题之一。干旱指数是开展干旱研究的一项重要工具。由于样本、模型以及参数的影响，利用干旱指数进行干旱的监测与评估时，得到的结果通常具有一定的不确定性。

以往研究中，样本不确定性对于干旱指数的影响研究相对较多。例如，洪兴骏等［2］采用Monte-Carlo 随机模拟方法验证了干旱指数（Streamflow drought index，SDI）计算的抽样不确定性；张瑞涵等［3］采用参数和非参数Bootstrap 方法评价了样本不确定性对标准化降水指数（Standardized precipitation index，SPI）的影响。在模型方面，干旱指数计算时需要用到概率分布模型来拟合相关数据，不同地区气候条件的差异导致计算时所选用的最优理论概率分布模型各不相同；有研究表明，Pearson-III分布是美国地区以及我国鄱阳湖流域计算SPI的最佳模型［4-5］，欧洲地区Weibull 分布比Gamma 分布的拟合效果更好［6］；广义正态分布更适合巴西地区多时间尺度SPI 的计算［7］；欧洲地区建议使用广义极值（Generalized extreme value，GEV）分布计算标准化降水蒸散指数（Standardized precipitation evapotranspi⁃ration index，SPEI）［8］等。在参数方面，以往研究更多针对不同参数估计方法的影响，Begueria等［9］对比了两种参数估计方法——最大似然估计法和无偏概率加权矩法在计算SPEI 时的性能。而模型参数估计误差本身以及不同理论概率分布模型对干旱评估结果带来的不确定性在现有研究中较少涉及。鉴于此，本文主要探讨不同概率分布模型以及参数估计误差这两种不确定性来源对干旱指数以及干旱评估的影响程度；由于SPEI 既考虑了降水、又考虑了蒸散发对干旱的影响，因此选择该指数作为待分析干旱指数。

黑河流域是我国西北地区第二大内陆河流域，干旱始终是该流域最主要的自然灾害之一［10］。近2000 年来流域累计发生旱涝灾害达251 次，旱灾占到70%以上［11］。全球变暖背景下，流域中下游的干旱现象日益严重，2001 年发生了1941—2001 年近60 a以来最严重的秋、冬、春三季连旱［12］。频繁的干旱灾害不仅致使当地自然生态环境异常脆弱，也进一步制约了经济社会的健康发展。黑河流域中游走廊平原是良好的发展农业地区，然而由于受到亚洲东岸西北气流和大地形边缘下沉气流的双重控制影响，该地区是全球同纬度有人类活动的最干旱的地区之一，农作物需水高峰期在每年4—6 月，同时期正是该流域的枯水期，导致夏灌“卡脖子”旱的矛盾异常突出［13］。研究以黑河流域为例，评估了9种概率分布模型以及模型参数估计误差对SPEI 以及对干旱强度、干旱峰值、干旱历时等特征变量的影响程度，从而为干旱的准确评估提供支撑，为防旱减灾工作中更加准确有效的抗旱决策提供理论支持，以避免可能造成的减灾能力不足或抗旱资源的浪费。

1 研究区概况

黑河流域位于河西走廊中部，地理位置介于97°37′～102°06′E，37°44′～42°40′N之间，流域面积近14.29×104km2，流域及站点位置如图1 所示。受西风带环流和极地冷气团的双重影响，研究区气候存在明显的南北差异与东西差异，跨越了3 个地理气候区，由南向北分别为：半干旱半湿润气候区、半干旱气候区和极度干旱的沙漠区［14］。上游南部山区多年平均降水量400～500 mm，多年平均气温1.5～2.0 ℃，气候冷凉；中游多年平均降水量100～150 mm，多年平均气温2.8～7.6 ℃；下游多年平均降水量则小于50 mm，下游额济纳平原多年平均气温为8.0 ℃。总的来看，全流域降水稀少但分布集中，日照时间长，蒸发作用强烈，昼夜温差大。近年来，从流域整体来看，其平均气温呈现出显著上升趋势，以额济纳旗站为代表，其增长速率达到了0.42 ℃·(10a)-1［15］，一定程度上加剧了流域的干旱问题。

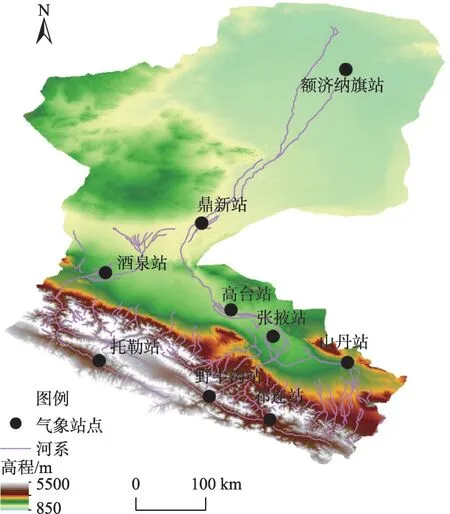
图1 黑河流域及气象站点位置示意图Fig.1 Location diagram of the Heihe River Basin and the meteorological stations

2 数据与方法

2.1 数据来源

选用流域内9 个国家级气象站作为研究站，站点基本信息见表1。考察数据的完整与连续性后，选用了1960—2015 年逐日降水量和气温数据集用于SPEI的计算，数据来源于国家气象科学数据中心（http://data.cma.cn/），数据质量良好。

表1 黑河流域气象站基本信息Tab.1 Basic information of the meteorological stations in the Heihe River Basin

2.2 研究方法

2.2.1 标准化降水蒸散指数（SPEI）和干旱特征变量Vicente-Serrano 等［16］在2010 年以SPI 的概念和计算方式为基础，提出了SPEI，与SPI 相比，SPEI 考虑了温度对干旱的影响，常用于气温敏感地区的干旱特征分析，并建议采用三参数的Log-Logistic概率分布模型来描述降水量与潜在蒸散发之间的差值变化。该指数的计算过程详见Vicente-Serrano等［16］研究。根据SPEI 值的大小，干旱可分为5 个等级（表2）。干旱事件的发生指的是干旱指数低于某一设定的阈值，例如SPEI值介于-1.5～-2.0之间时，表明一次严重干旱事件发生了。根据游程理论［17］，干旱历时即干旱指数介于阈值水平的时间；干旱强度定义为一次干旱事件中的干旱指数累加值与干旱历时的比值；干旱峰值定义为一次干旱事件中的干旱指数最小值。

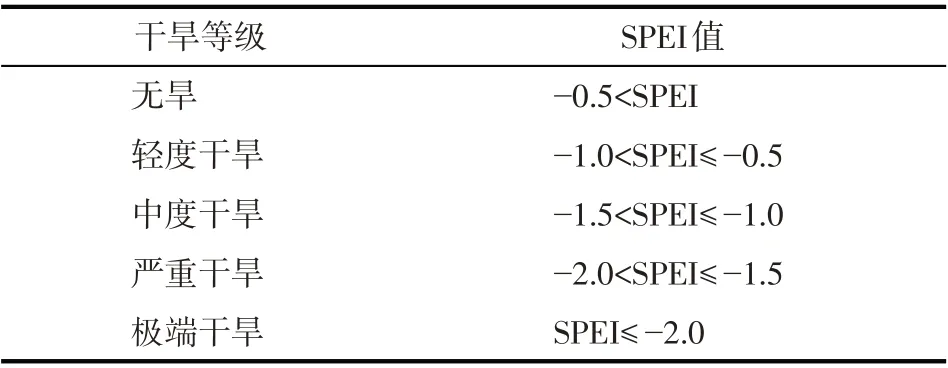
表2 基于SPEI的干旱等级划分Tab.2 Drought classification based on standardized precipitation evapotranspiration index(SPEI)

2.2.2 概率分布模型与拟合优度检验为评估不同概率分布模型对SPEI估算的影响，选取9种模型进行计算，具体包括三参数分布Log-Logistic（LL3）、Log-Normal（LN3）、GEV、Pearson-III（PE3）和Weibull（WEI3），两参数分布Normal、Logistic、Chi-Square 和Cauchy。各概率分布模型的概率密度函数见参考文献［13］。采用最大似然估计法对不同分布模型进行参数估计，采用Kolmogorov-Smirnov（K-S）和Anderson-Darling（A-D）两种检验法对分布模型进行拟合优度检验。K-S检验法是在经验分布函数的基础上，计算给定累积分布函数和经验分布函数的差值最大值来进行拟合优度检验，这种方法的优点是不需要事先假设拟检验数据服从的具体分布；A-D检验是K-S检验的一种改进，它对分布两端的离群值更为敏感。两种检验的计算方法详见Fadhilah等［18］研究。

2.2.3 多元正态法采用多元正态法量化由参数估计误差导致的干旱指数估计值的不确定性［19-20］，具体步骤如下：

（1）使用LL3概率分布模型分别拟合各月降水量（P）与潜在蒸散发（PET）的差值累积序列Xj=(xj1,xj2,…,xjn)，得到最优参数集(α*,β*,γ*)以及对应的方差-协方差矩阵，其中j表示月份，n表示样本量大小。

（2）在渐近正态假设的最优参数集和方差-协方差矩阵的基础上，随机生成N组参数集[(αj1,βj1,γj1) ,(αj2,βj2,γj2),…,(αjN,βjN,γjN)]，其中N取1000。

（3）计算每组参数对应的SPEI，N组参数共对应N组SPEI。

（4）基于N组SPEI，定义第（a/2）和第（1-a/2）个百分位数分别为SPEI 的置信区间（CIs）下限和上限，a取0.05，该置信区间即是考虑参数估计误差影响的SPEI的不确定性区间。

3 结果与分析

3.1 概率分布模型及其影响

3.1.1 拟合优度检验结果首先采用Thornthwaite方法计算各站点的逐月潜在蒸散发［16］，以此为基础，使用不同概率分布模型拟合降水量与潜在蒸散发的差值序列。图2 以1 月为例，给出了不同概率分布模型对差值序列的拟合效果。K-S检验和A-D检验在0.05 显著性水平下的临界值分别达到0.18和2.50，若统计值低于这一临界值，则说明该数据序列在0.05显著性水平下通过了相应检验，反之则表明没有通过。

由图2可以看出，所有站点K-S和A-D检验统计量均低于临界值，说明这些分布都可以用来拟合该序列，效果良好。图中虚线黑框表示相应站点统计量的最小值，可以看出，9 个中有8 个最优模型是三参数概率分布模型，其中LL3拟合效果最好，对应的统计量最小值最多，占到61%；其次是LN3 和WEI3分布。两参数模型中，Logistic 分布拟合效果最好，有12个统计值最小，占比达到67%。Cauchy分布的拟合效果最差。

图2 不同概率分布模型对1月数据序列的检验统计值Fig.2 Statistical values of tests of different probability distribution models for January data series

此外，其余月份数据序列的拟合检验结果也表明，LL3与Logistic 分布分别是三参数和两参数模型中拟合效果最优的分布模型，分别有48%（104）和54%（116）的统计量最小。

3.1.2 概率分布模型对干旱指数的影响虽然所有分布均适用于拟合研究区降水量和蒸散发的差值序列，但不同分布计算得到的SPEI 是否接近，不同分布的选取对SPEI带来的不确定性有多大，还需要进一步探究。由此采用所有分布分别计算各站点的SPEI，并比较各分布与最优分布（LL3）计算结果的差异。

图3 以流域上游野牛沟站、流域中游酒泉站和流域下游额济纳旗站为例，展示了各分布与最优分布计算的SPEI的残差值散点图。可以看出，以SPEI等于0为轴，当-1＜SPEI＜1时，各站点的残差最大差异值介于-0.24～0.31 之间；随着SPEI 绝对值的增加，差异也随之增大；当SPEI 增加至±1.5（严重干旱）时，差异显著增加，最大残差值高达-0.89～-1.49。与其他分布相比，Cauchy 导致的差异最大（黄色曲线），Cauchy 分布计算的指数值更加居中，极端干旱或湿润的事件较少；例如，1992年3月野牛沟站和1970年5月额济纳旗站，Cauchy分布计算的数值分别为-1.37和1.45，属于中度干旱、中度湿润，而其他分布模型计算的SPEI的平均值分别为-2.09和2.30，属于极度干旱和极端湿润。另外，除Cauchy分布外，有7个站点Logistics分布给出的差异最大。

图3 各分布与三参数Log-Logistic分布计算的SPEI的残差值Fig.3 Residuals of SPEI values derived from the alternative distributions and the optimal distribution(three-parameter Log-Logistic)

图4a 给出了由不同概率分布模型导致的所有站点SPEI 的差异图，图中基本呈现出随着SPEI 的绝对值的增加（越湿润或者越干旱），差异随之增大的趋势，尤其对于中度干旱（或湿润）以上等级。当无旱和轻旱时，SPEI 的差异范围为［0.03，0.45］；当中度干旱（或湿润）时，差异范围为［0.09，0.51］；当严重干旱（或湿润）时，差异范围增加至［0.26，0.96］；极端干旱（或湿润）时差异范围为［0.62，1.49］。

图4 不同分布和参数估计误差对SPEI的影响Fig.4 Effects of different probability distribution models and parameter estimation errors on the SPEI index

3.1.3 概率分布模型对干旱特征变量的影响基于游程理论提取出所有站点的干旱历时、干旱强度和干旱峰值3 种特征变量，然后按表2 的干旱等级划分标准进行划分。图5给出了不同干旱等级下所有站点干旱特征的统计图，根据统计可知，所有站点轻度、中度、严重和极端干旱强度分别是-0.74，-1.22，-1.69 和-2.01。由不同分布导致的轻度、中度、严重和极端干旱强度的95%置信区间分别是［-0.81，-0.69］、［-1.26，-1.10］、［-1.77，0］、［-2.36，0］，随着干旱等级的增加，干旱强度的不确定性随之增大，尤其对于严重干旱和极端干旱，其95%置信区间宽度几乎达到轻度和中度干旱的11～20 倍（图5a）。4个等级干旱峰值的95%置信区间分别是［-1.00，-0.98］、［-1.50，-1.34］、［-2.00，0］、［-2.48，0］，也是随着干旱等级的增加，其不确定性随之增大，严重干旱和极端干旱峰值的不确定性增加尤为显著（图5b）。对于干旱历时，不同等级干旱程度的不确定性虽然存在差异，但差异不大，轻度干旱历时不确定性最小，其次是严重干旱和极端干旱，中度干旱历时不确定性最大，是轻度干旱不确定性的2.7倍（图5c）。与干旱强度和干旱峰值相比，干旱历时的不确定性在不同干旱等级之间差异小的多。

图5 不同分布和参数估计误差对干旱特征变量的影响Fig.5 Effects of different probability distribution models and parameter estimation errors on drought characteristic variables

3.2 参数估计误差及其影响

3.2.1 参数估计及其误差利用最大似然法计算得到LL3分布形状参数（shape）、尺度参数（scale）和位置参数（location）参数值，野牛沟站、酒泉站和额济纳旗站的结果如表3所示，表中以1月为例，分别给出了参数最优值和参数估计值的95%置信区间。

表3 三参数Log-Logistic分布参数最优值及95%置信区间Tab.3 Optimal values and 95%confidence intervals for the parameters of three-parameter(Log-Logistic)distribution

3.2.2 参数估计误差对干旱指数的影响图6给出了3 个站点SPEI 和根据多元正态法得到的SPEI 的95%置信区间，从图中可以看出，SPEI 越大或越小，对应的置信区间越宽。

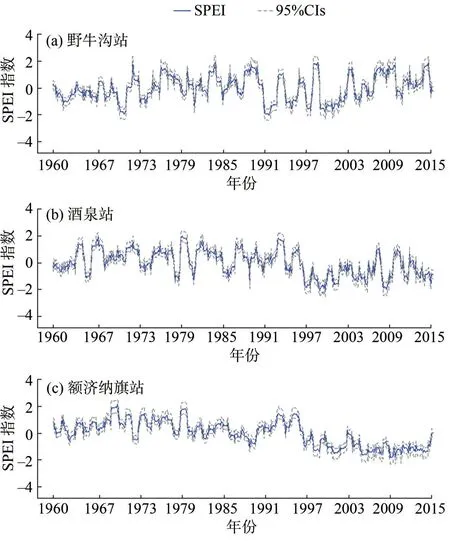
图6 SPEI及考虑参数估计不确定性的95%置信区间Fig.6 Estimations of SPEI and the 95%confidence intervals with considering the uncertainty of parameter estimates

图4b 给出了由参数估计不确定性导致的SPEI的95%置信区间。从图中可以看出，从轻度干旱（或湿润）到中度干旱（或湿润）再到严重干旱（湿润），95%置信区间宽度明显呈现增加趋势。当无旱和轻旱时，95%置信区间为［0.53，0.79］；中度干旱（或湿润）时，置信区间为［0.59，0.93］；严重干旱（或湿润）时，置信区间增加至［0.64，1.03］。

3.2.3 参数估计误差对干旱特征变量的影响图5同时给出了由参数估计不确定性导致的不同干旱等级下所有站点的干旱特征。轻度、中度、严重、极端4 个等级干旱强度的95%置信区间分别为［-0.79，-0.72］、［-1.30，-1.14］、［-1.80，-0.66］、［-2.28，0］，干旱峰值的置信区间分别为［-1.00，-0.98］、［-1.50，-1.40］、［-2.00，-0.71］、［-2.48，0］，干旱历时的置信区间分别为［7.43，13.15］、［8.00，18.33］、［1.28，15.60］、［0，15.73］；干旱等级越高，干旱强度和干旱峰值的不确定性越大，极端干旱和严重干旱的不确定性范围明显大于轻度和中度干旱的不确定性；对于干旱历时，极端、中度、严重干旱历时的不确定性范围比较接近，轻度干旱历时的不确定性最小（图5）。

4 讨论

根据拟合优度检验结果，选取的9 种分布均适用于研究区降水量与潜在蒸散发差值序列的拟合，三参数模型中LL3 分布适用性最强，两参数模型中Logistic 分布适用性最强（图2）；如果仅考虑拟合效果，Logistic 分布由于其仅包含2 个参数，计算相对简单，因此可以作为拟合降水量与潜在蒸散发差值序列的候选分布；但通过比较SPEI 可以发现，基于Logistic 分布与基于LL3 分布计算得到的指数值在极值处存在较大差异；虽然两参数模型参数少、计算简单，但该模型会对干旱指数的计算带来较大不确定性（图3、图4）。

通过计算不同概率分布模型对应的SPEI 可以发现，概率分布模型是导致SPEI存在不确定性的来源之一。Vergni 等［21］在其研究中也发现，除数据序列长度外，概率分布模型是导致SPI 存在不确定性的主要来源；Laimighofer等［22］认为，概率分布模型对SPI和SPEI不确定性的相对贡献程度较大。本研究还发现，干旱（或湿润）等级越高，由不同分布模型导致的SPEI的不确定性越大，尤其对于严重和极端干旱，不确定性增加尤为显著，甚至会影响到干旱等级的评估（图3、图4）。另外，分布模型还对干旱强度、干旱峰值、干旱历时等特征变量的评估也带来一定的不确定性。随着干旱等级的增加，由其导致的干旱强度、干旱峰值的不确定性均随之增大，严重和极端干旱的不确定性增加尤为明显，其不确定性范围达到轻度和中度干旱的10 倍以上（图5）；这说明由概率分布模型导致的严重和极端干旱强度和干旱峰值的不确定性很大，不可忽视。其导致的干旱历时的不确定性并未随干旱等级的变化而发生显著变化，不同等级之间干旱历时的不确定性范围比较接近（图5）。

模型参数估计误差也会导致SPEI 存在一定的不确定性［22-23］。Zhang 等［23］研究表明，SPI 干旱指数越极端，由模型参数估计误差导致的该指数不确定性越大；本文选用的是SPEI，研究结论与其类似，即SPEI越极端，由模型参数估计误差导致的SPEI不确定性越大（图4、图6）。另外，干旱等级越高，由参数估计误差导致的干旱强度、干旱峰值的不确定性也越大，极端干旱和严重干旱的不确定性范围明显大于轻度和中度干旱的不确定性范围；不同等级之间干旱历时的不确定性范围比较接近（图5）。

与概率分布模型的结果相比，尤其对于轻度、中度、严重干旱，由参数估计误差导致的SPEI 的95%置信区间更宽，即不确定性更大；由参数估计误差导致的严重干旱强度及干旱峰值、中度干旱历时的不确定性偏小，而严重和极端干旱历时的不确定性则有所偏大，其余干旱特征变量的不确定性范围则比较接近。这也说明，两种不确定性来源对干旱特征评估均会产生影响，尤其对严重和极端干旱的强度和峰值的影响较大。因此，在进行干旱评估时，需要重点考虑最优概率分布模型的选取以及最佳参数估计方法，从而降低其导致的干旱评估结果的不确定性，为精准干旱评估预测预报提供支持。

需要指出的是，除文中讨论的两种不确定性来源外，干旱评估过程中还存在其他不确定性来源，如不同潜在蒸散发估算方法等；Aadhar 等［24］研究指出，潜在蒸散发估计方法对干旱评估最终结果的不确定性贡献很大；限于数据资料原因，文中仅采用Thornthwaite方法计算各站点潜在蒸散发，因此也会对评估结果带来一定的不确定性，这方面将在以后的研究中予以综合考虑。

5 结论

本文以黑河流域及SPEI 为例，探讨了9种概率分布模型和参数估计误差这两种不确定性来源对干旱指数以及对干旱强度、干旱峰值、干旱历时等特征变量不确定性的影响，主要结论如下：

（1）概率分布模型的选择对干旱评估的可靠性具有重要意义。总体而言，三参数Log-Logistic与两参数Logistic 分布都能较好地拟合黑河流域的SPEI。三参数概率分布模型的拟合效果比两参数的拟合效果更优，两参数模型参数少、计算简单，虽然可作为拟合降水量与潜在蒸散发差值序列的备选分布，但在计算SPEI 时容易引起较大的不确定性。随着干旱等级的增加，由不同概率分布模型导致的SPEI的不确定性会随之增大，从而影响干旱评估结果的可靠性。

（2）参数估计误差也会导致SPEI 及干旱评估结果存在一定的不确定性。SPEI越极端，模型参数估计误差导致的SPEI的不确定性越大；干旱等级越高，干旱强度和干旱峰值的不确定性越大，极端干旱和严重干旱的不确定性范围远大于轻度和中度干旱的不确定性。

（3）两种不确定性来源对干旱评估均会产生影响，尤其对严重和极端干旱的强度和峰值的影响较大。与分布模型相比，参数估计误差导致的轻度、中度、严重干旱的SPEI 的不确定性更大，严重和极端干旱历时的不确定性更大。这说明，在进行干旱精准评估时，以上两种不确定性来源均需考虑；通过选取最优概率分布模型以及最佳参数估计方法，可以降低干旱评估结果的不确定性。