面向控制的柴油机PPCI燃烧预测模型研究

桂勇，陈自强，姚晔，杨凯，章雍，石磊

(1.中船动力研究院有限公司，上海 201208；2.上海交通大学机械与动力工程学院，上海 200240)

柴油机部分预混压燃(PPCI燃烧)[1]采用了部分均质充量压燃[2]和部分扩散燃烧结合的方式，具有同时显著降低NOx与PM排放的优势，但其对油气混合状态与边界条件敏感，使得面向控制的燃烧建模难度大[3-5]。

针对PPCI燃烧建模困难的问题，国内外学者进行了多方面研究。大连理工大学的解茂昭等[6]构建了包括 40 种组分、65 个反应的化学动力学骨架机理预测燃料燃烧和排放数据。Kong[7]与Babajimopoulos[8]等采用多维模型与化学动力学模型结合的方式研究了PPCI燃烧过程，获得了缸内燃烧特征变化数据。美国俄亥俄州立大学Marcello等[9]使用单韦伯函数进行HCCI燃烧过程建模。大连理工大学Yang等[10]基于韦伯函数线性化的方法建立了PPC燃烧模型。康明斯公司Lyle等[11]开发了PCCI发动机燃烧始点预测的半物理模型，对PCCI发动机燃烧始点有较好的预测功能，结合VVA、VGT与喷油系统可以实现燃烧始点控制。丰田公司Nishida[12]与日本东京大学Yamasaki等[13]都建立了PCCI燃烧多段喷油放热率模型，建模难点在于每段燃油喷射时缸内状态都不一致，因此需要较准确地计算油雾分布状态，对控制器计算速度要求较高。国内外学者对PPCI发动机喷油参数优化开展了研究，从燃烧优化方面确定了喷油控制策略[14-15]。清华大学方成[16]与意大利都灵理工大学Ferrari等[17]都采用了PID控制器对柴油PCCI燃烧的IMEP与CA50进行闭环控制。奥地利林茨大学的Ortner等[18]使用MPC控制器实现了与PPCI特征相同的低温燃烧发动机可变截面涡轮增压器(VGT)与EGR系统的控制。可见，如何实现PPCI燃烧状态预测是实现其有效控制的关键。

为了建立面向控制的PPCI燃烧模型，本研究以一台126 mm单缸柴油机为研究机型，开展了喷油参数对燃烧参数的敏感性分析，建立了PPCI柴油机韦伯函数线性化燃烧模型，并对模型参数进行标定与回归分析，实现了气缸压力与放热率的预测。

1 试验台架及测试工况

本试验所用台架为一台自主设计的单缸、直喷、水冷、4冲程柴油机，基本性能参数见表1。试验过程中，采用缸内燃油预喷结合大EGR率实现柴油PPCI燃烧，通过预喷调整预混燃烧油量，通过EGR来实现燃烧过程控制。试验台架安装有湘仪FC2005测控系统，由NI-9222数据卡采集缸压信号与相位信号，采用自主开发的基于LabVIEW的燃烧分析程序，实现了放热率与燃烧参数实时计算。

在单缸机台架上开展不同控制参数试验，试验数据用于标定燃烧状态辨识模型参数，共45个工况点，包含低中高3个负荷下的变预喷正时(θP,INJ)、变预喷脉宽(tP,INJ)、变主喷正时(θM,INJ)试验，每个工况点设定θP,INJ、tP,INJ、θM,INJ3个参数。试验中，通过改变主喷脉宽(tM,INJ)使IMEP保持不变。试验工况见表2。

表1 单缸机基本参数

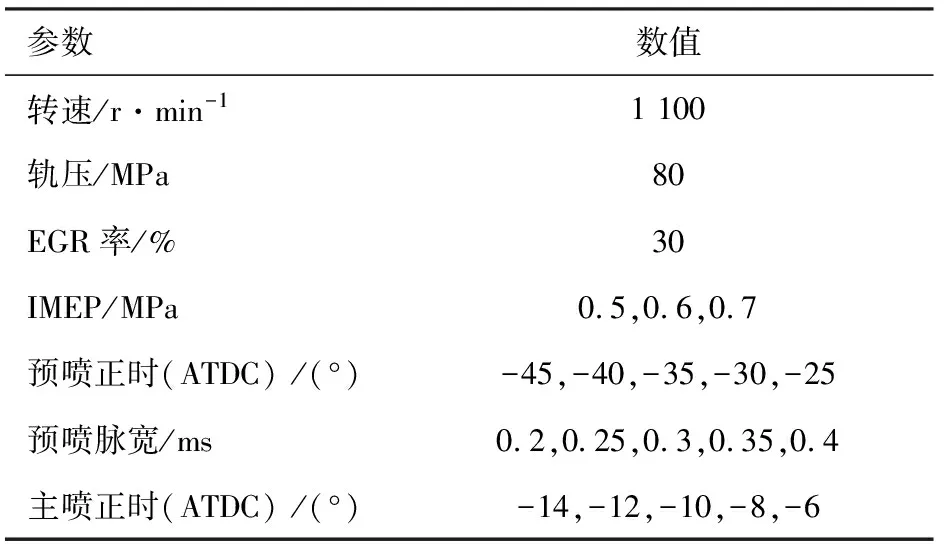
表2 试验工况表

2 PPCI喷油参数对燃烧参数敏感性分析

为了探究不同输入参数对输出参数的影响程度，采用敏感性分析定量研究系统输出变化对输入条件的敏感程度。将归一化输入参数X对输出参数Y的敏感性定义为式(1)，敏感性的绝对值越大则表示输入X对输出Y的影响越显著。

(1)

2.1 喷油参数对滞燃期的敏感性分析

采用敏感性分析的方法，衡量不同IMEP下3种喷油参数变化对滞燃期(tID)的敏感程度(见图1)。敏感性分析图采用箱型图形式绘制，矩形盒体表示75%的敏感性指标分布区域，盒体内的横实线表示中位数，上下边界表示敏感性的最大值与最小值。敏感性分析图中，敏感性的绝对值越大表示输出参数对输入参数越敏感。对比可得预喷正时与预喷脉宽对滞燃期的敏感性较大，且不同IMEP下敏感性发生变化，而主喷正时对滞燃期较不敏感。

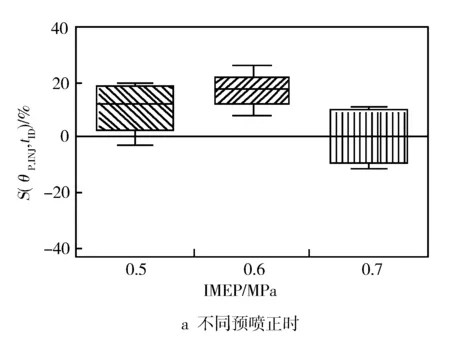
图1 喷油参数对滞燃期的敏感性分析

2.2 喷油参数对CA50的敏感性分析

图2示出不同喷油参数对CA50的敏感性分析结果。从图中可以看出，主喷正时对CA50的敏感性要显著大于另外两个喷油参数，其绝对值超过100%，表明主喷正时对CA50起主导作用。

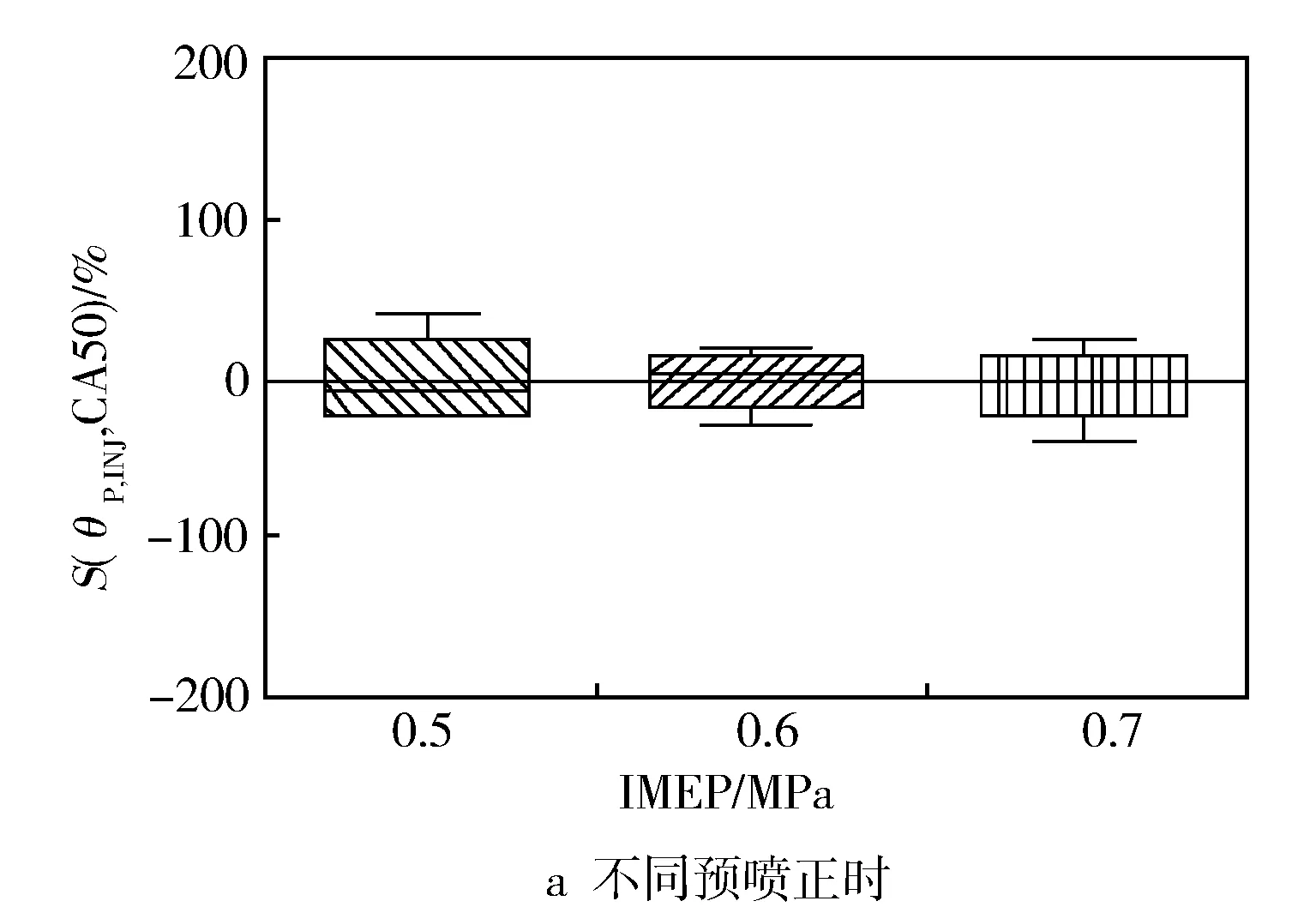
图2 喷油参数对CA50的敏感性分析

2.3 喷油参数对燃烧持续期的敏感性分析

图3 示出不同喷油参数对燃烧持续期(tCD)的敏感性分析结果，燃烧持续期与预喷正时呈二次关系，与预喷脉宽正相关，且对于主喷正时变化较不敏感。

图3 喷油参数对燃烧持续期的敏感性分析

2.4 喷油参数对最大压升率的敏感性分析

图4示出不同喷油参数对最大压升率(PIRmax)的敏感性分析结果，可以看出3个喷油参数都对最大压升率较为敏感，其中主喷正时的敏感程度最高。

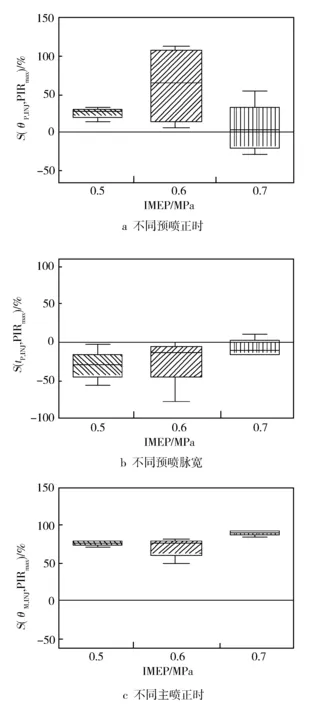
图4 喷油参数对最大压升率的敏感性分析

3 基于喷射参数的PPCI燃烧预测模型搭建

在分析不同喷油参数对燃烧敏感性的基础上，开展了基于喷射参数的PPCI燃烧预测模型研究。

3.1 基于韦伯函数线性化的燃烧预测模型

韦伯(Wiebe)函数被广泛应用于柴油机燃烧建模中，一般形式的韦伯函数公式如式(2)所示：

(2)

式中：x(θ)为燃烧分数，表示已燃燃料占总燃料之比；θ为曲轴转角；θSOC为燃烧始点；θEOC为燃烧终点；a和m为韦伯参数。

本研究采用韦伯函数线性化处理的建模方法，将韦伯函数式(2)进行变形处理，如式(3)所示：

(3)

将试验实测累计放热率x(θ)代入式(3)，得到放热率线性化处理后的f(θ)，如图5所示。

图5 韦伯函数线性化处理

将放热率线性化后，可以看出线性化函数具有明显的两段形式：预喷燃料的低温放热阶段和主喷燃料的主放热阶段。在两个阶段的放热过程中，都有一个燃烧速率的突变点，可以认为预混燃烧主要发生在突变点之前，扩散燃烧主要发生在突变点之后。曲线斜率代表该阶段的燃烧速率。

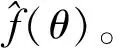
(4)

3.2 燃烧预测模型参数标定

图7所示为不同预喷脉宽下的模型参数标定结果。随着预喷脉宽增加，预混比例增加，低温放热阶段相位提前，反应速率增加，θP,IGN、θt1提前，k1、k2增加；主燃阶段相位推迟，燃烧速度下降，θM,IGN、θt2推迟，k3、k4下降。从图中可观察到各模型参数与预喷脉宽呈现线性关系。

图8所示为不同主喷正时下的模型参数标定结果。由于预喷燃油的低温放热起始于主喷正时之前，因此主喷正时不影响θP,IGN与θt1；而θM,IGN、θt2与主喷正时几乎成线性关系。由于低温放热的相位不随主喷正时变化、主燃阶段相位随主喷正时线性变化，因此k2随主喷正时的推迟而减小。

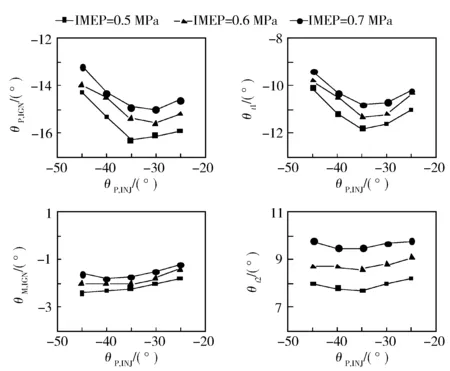
图6 不同预喷正时下的模型参数

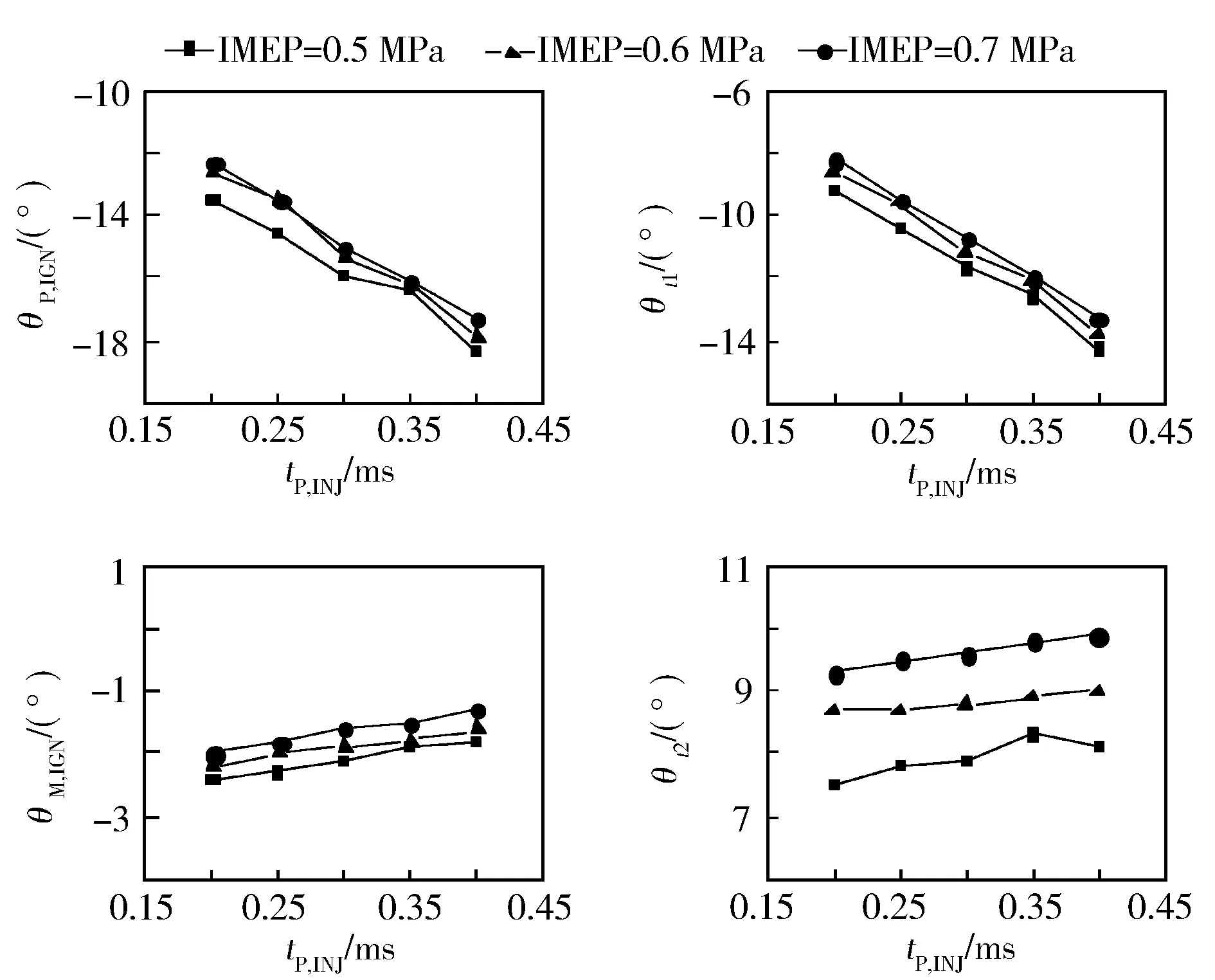
图7 不同预喷脉宽下的模型参数

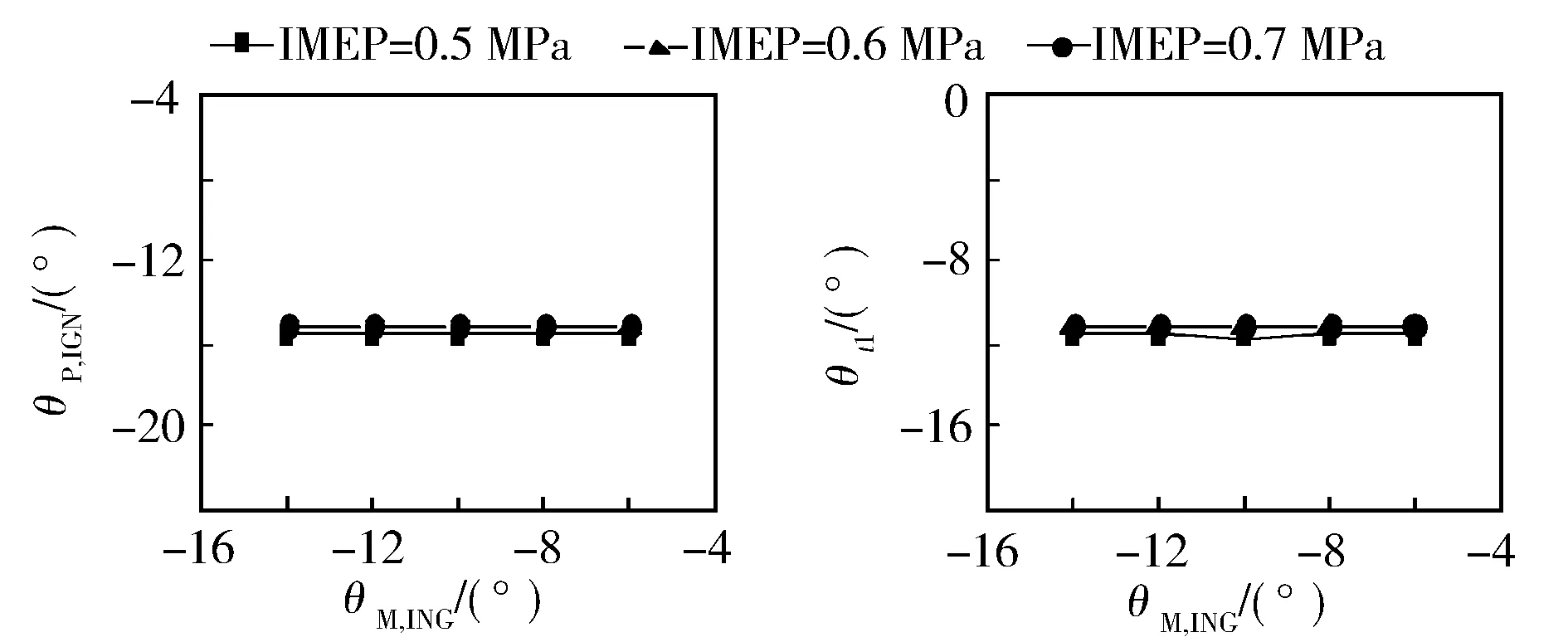
图8 不同主喷正时下的模型参数

由图6至图8可知，θP,IGN、θt1与θP,INJ呈二次函数关系，其余模型参数与喷油参数均呈明显的线性关系，因此可以将8个模型参数作为因变量、4个喷油参数作为自变量，采用多元回归分析的方法求解模型参数，用最小二乘法求取系数B矩阵，计算得出回归分析结果(见表3)，将系数矩阵与喷油参数代入式(5)即可算出相应的模型参数值。

y=b1+b2θP,INJ+b3tP,INJ+b4θM,INJ+

b5tM,INJ+b6θP,INJ2。

(5)

3.3 放热率及缸压重构

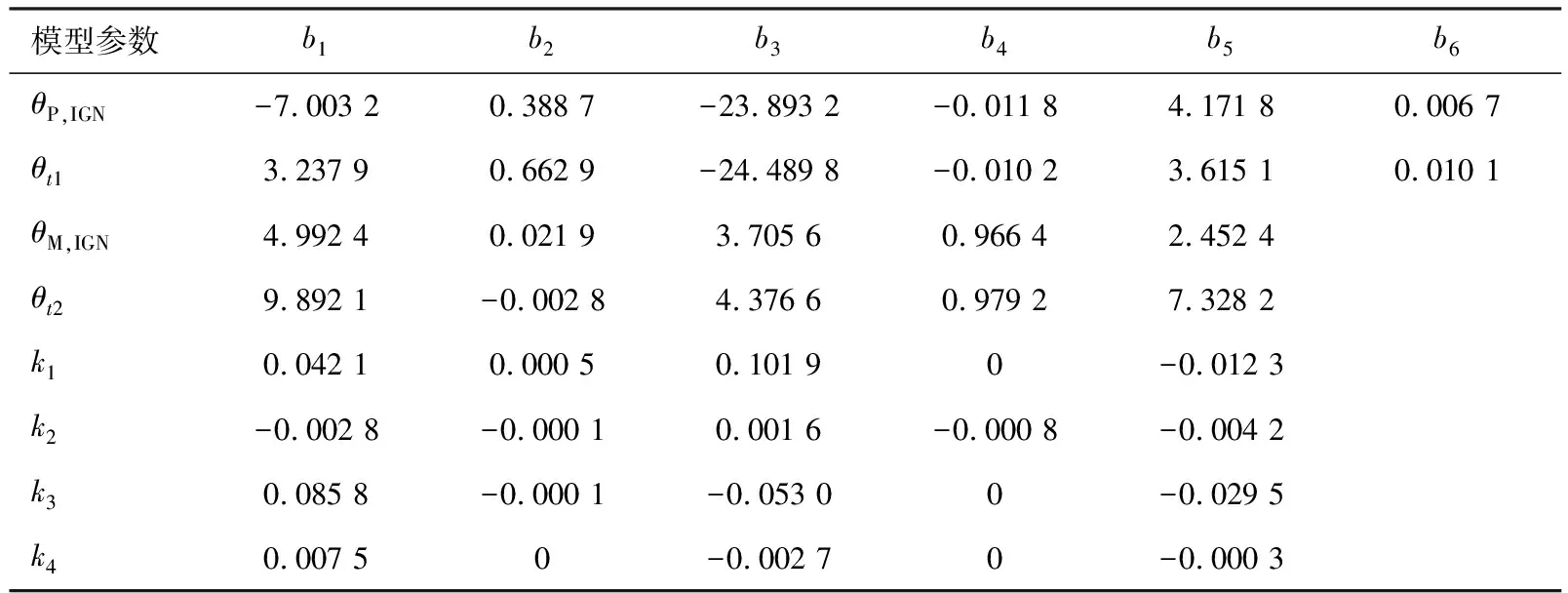
表3 燃烧模型参数回归分析结果

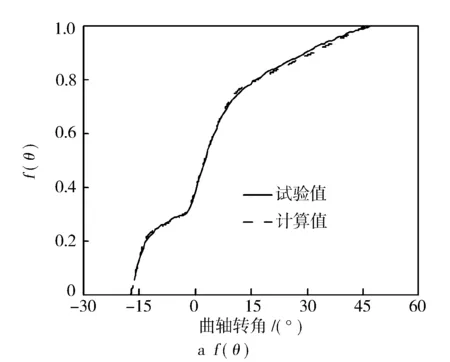
图9 f(θ)放热率计算值与试验值对比图

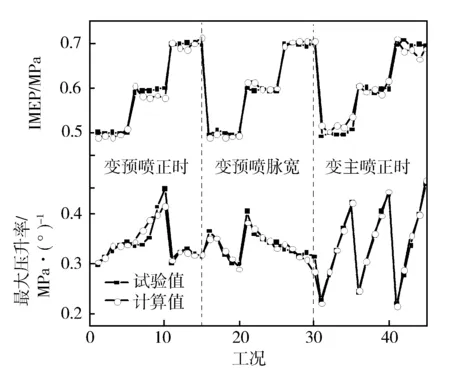
图10 IMEP与最大压升率计算误差

4 结束语

基于126 mm缸径单缸柴油机试验台架，将PPCI发动机燃烧过程作为多输入多输出系统，进行了喷油参数对燃烧参数的敏感性分析，建立了面向控制的PPCI发动机韦伯函数线性化燃烧，实现了通过输入喷油参数，实时输出放热率、缸压等参数。

进行了敏感性分析，发现滞燃期、CA50、燃烧持续期、最大压升率受某一或某几个喷油参数影响明显，因此利用喷油参数进行燃烧建模具有可行性。

基于韦伯函数线性化方法处理实测放热率，观察出PPCI燃烧过程存在明显的分段现象，提出了采用4段线段共8个模型参数对放热率线性化函数进行描述的燃烧建模方法。

对45组变喷油参数试验工况进行标定，结果表明模型参数与喷油参数之间存在明显的一次线性或二次函数关系，采用多元回归分析的方法建立了喷油参数到模型参数之间的数学关系，大部分模型参数的计算值与标定值相关系数大于0.98。