退磁场对磁致伸缩应力耦合谐振磁传感器灵敏度的影响研究*
张 闯,卞雷祥,石 昱,黄子军
(南京理工大学机械工程学院,江苏 南京 210094)
常见的磁致伸缩材料有铽镝铁合金(Terfenol-D)、Galfenol 合金、铁钴钒合金和铁镍合金等,其中铽镝铁合金和Galfenol 合金具有高磁致伸缩系数、压磁系数[1-3],常被用于设计高性能的磁场传感器[4-5]。将磁致伸缩材料与压电材料复合得到磁电敏感器件。 Bush 等[6]将磁致伸缩材料FeGa 与压电材料PZT 复合,利用磁致伸缩层的磁致伸缩效应和压电层的压电效应的乘积特性来实现磁电性能转换,磁电电压系数达到8.7 V/cmOe。 Espinosa 等[7]制备了Galfenol/BaTiO3、CoFe2O4/BaTiO3和Terfenol-D/BaTiO3复合材料,磁电电压系数分别为1.6 V/cmOe、0.2 V/cmOe和0.3 V/cmOe,由Galfenol 合金组成的复合材料具有更高的磁电电压系数。 Dong 等[8]采用环形的Terfenol-D/PZT 复合磁电材料设计成一种圆环形的磁场传感器,复合磁电材料的灵敏度为2.2 V/Oe,最小可探测磁场为6×10-12T。 Caponero 等[9]设计了Galfenol/FBG 光栅复合的磁场传感器,嵌入FBG光栅的光纤通过胶水粘合在Galfenol 合金上,在一定的磁场下,Galfenol 产生的磁致伸缩位移传递到FBG 光栅使其波长改变,通过对Galfenol 合金施加机械应力达到控制测量范围的目的,磁场检测范围增加了几十kA/m。 按磁荷的观点,磁致伸缩材料磁化时将在两端面产生磁荷,材料内部产生退磁场减弱磁化[10],退磁场的大小与磁化强度的大小成正比,而退磁因子Nd的大小只与磁体的磁导率和尺寸比有关。 Apicella 等[11]考虑到施加机械应力带来的结构复杂性,在之前的研究基础[9]上通过调整Galfenol 合金棒的长径比控制退磁场的大小,从而实现了对Galfenol/FBG 光栅复合的磁场传感器磁场检测范围的控制,结果表明长度为10 mm、直径为4 mm,长径比为2.5 的Galfenol/FBG 光栅复合的磁场传感器磁场检测范围可达125 mT,比长度为50 mm、直径为5 mm,长径比为10 的磁场检测范围增大了约4 倍。 Loyau 等[12]研究了厚度和体积比不同的ferrite/PZT/ferrite 层合材料退磁场对磁电电压系数的影响,当层合材料厚度减小及体积比增大时退磁场减小,磁电电压系数增大。 Pan 等[13-14]研究了形状和尺寸对Ni/PZT/Ni 层合材料磁电电压系数的影响,正方形样品的退磁因子小于三角形样品,因此,正方形样品的磁电电压系数可达40 V/cmOe,是三角形样品的2.7 倍,而当形状相同,样品的长度增长时退磁因子减小,磁电电压系数随之增大。 Du等[15]通过对比FeGa/BaTiO3/FeGa 层状复合结构中无退磁场的环状样品和有退磁场的实心碟片样品的磁电性能,研究退磁场对其磁电性能的影响,无退磁场的环状样品在340 Oe 的偏置磁场下磁电电压系数达到最大约220 mV/cmOe,有退磁场的实心碟片样品在750 Oe 的偏置磁场下磁电电压系数达到最大约62.5 mV/cmOe,因此,采用闭环的方式也可以提高磁电复合材料的磁电电压系数。
Bian 等[16]设计了一种FeGa/石英音叉复合谐振式磁场传感器,在一定的直流磁场下,磁致伸缩层产生的磁致伸缩力传递到双端固定音叉,从而改变双端固定音叉的谐振频率,通过对谐振频率进行测量即可测量磁场,灵敏度为3.5 Hz/Oe。 本文采用退磁因子计算经验公式与Maxwell 电磁仿真相结合,分析了不同长度FeGa 磁致伸缩合金的退磁因子,并将退磁因子代入非线性磁致伸缩模型,预测了退磁场对FeGa 合金磁致伸缩性能和FeGa/石英音叉谐振器复合谐振式磁场传感器灵敏度的影响。 利用多种不同长度FeGa 合金与石英音叉谐振器复合制备谐振式磁场传感器样件进行实验,实验结果与理论预测结果基本吻合。
1 应力耦合谐振式磁场传感器结构及原理
设计的谐振式磁敏感单元的结构如图1 所示,由不同长度的FeGa 合金片(10.6 mm×1.4 mm×0.6 mm、20 mm×1.4 mm×0.6 mm、30 mm×1.4 mm×0.6 mm),两个石英垫片以及一个双端固定音叉(Double-ended tuning fork,DETF)谐振器复合组成。在长度方向(纵向)磁场作用下,FeGa 合金由于磁致伸缩效应产生纵向磁致伸缩应力,该应力通过石英垫片传递到石英音叉谐振器纵向,导致音叉谐振器的谐振频率发生改变。 DETF 石英音叉的两根梁作180°反相、对称的弯曲振动,从而两个梁在末端结合处所产生应力和力矩相抵消,不会传递到音叉两端的固定区域。 石英音叉谐振器的这个结构特点也决定了复合传感器结构中磁致伸缩材料的磁机阻尼被隔离,不会传递到音叉谐振器,从而复合谐振式磁传感器的Q 值主要取决于石英音叉谐振器。 采用传统的四电极方法设计了音叉振梁的涂布电极,即可使音叉工作于所需要的弯曲振动模态[16]。

图1 谐振式磁敏感单元结构
可以采用门振荡电路激励音叉谐振器产生振荡信号输出[17],输出信号为准数字频率信号(方波),其频率值由音叉谐振器决定。 双端固定石英音叉谐振器的尺寸如表1 所示,具体的设计过程和制备工艺可参考Bian 等前期发表的论文[16]。
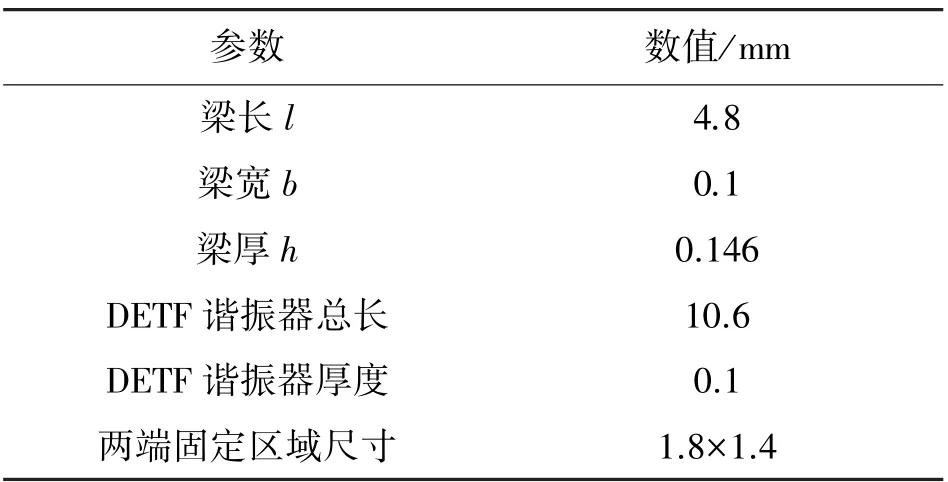
表1 DETF 谐振器尺寸
FeGa 合金具有非线性磁致伸缩特性,根据郑晓静等提出的非线性磁致伸缩本构模型(Z-L 模型)[18],得到仅考虑零预应力(σ=0)时的磁致伸缩系数表达式:

在静态磁场Hext作用下,磁致伸缩材料产生的磁致伸缩力为:

式中:Em和S分别为磁致伸缩材料在磁场H时的弹性模量和应变,Am为磁致伸缩材料的横截面积。 由于粘胶层的弹性模量远小于DETF 谐振器、石英垫片和FeGa 合金,所以磁致伸缩力Fm传递给DETF谐振器过程中,胶层不可避免发生剪切形变,故在传递过程中存在损失。 假设传递效率为β(0≤β≤1),结合式(3)、式(4),实际上作用到音叉谐振器纵向的力为:
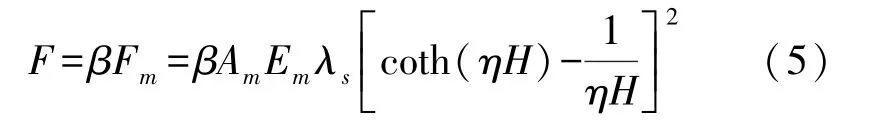
双端固定石英音叉谐振器的两个梁工作在180°反相对称的弯曲振动模式。 对于一个弯曲振动的梁,其谐振频率fr与梁长度方向所受力F的关系为[19]
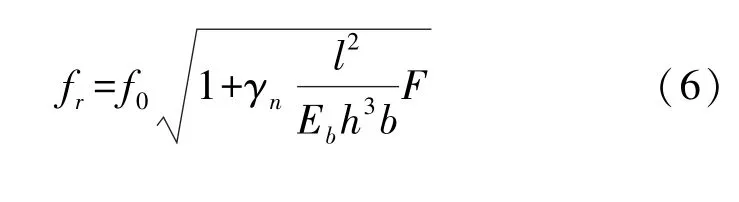
式中:

Eb=86 GPa 和ρ=2 650 kg/m3分别为石英梁的杨氏模量和密度[16];l,h和b分别为梁的长度,厚度和宽度;αn、γn为常数,在基频振动模态下,α0和γ0分别为4.730 00 和0.294 93;f0为梁在长度方向受力为零时的谐振频率。
2 退磁场对磁场传感器的影响分析
磁致伸缩材料FeGa 合金在外加磁场Hext中磁化时,在磁体内部产生退磁场,其方向与磁化场方向相反,导致磁致伸缩材料内部的实际磁场H与外加磁场Hext不相等,实际磁场H如下式所示:
H=Hext-NdM(8)
式中:M为磁化强度,Nd为退磁因子。
只有在磁体是椭球体时退磁因子才有唯一确定的值,在其他形状下因退磁场不均匀分布,只能取近似值和平均值[20-21]。 根据B=μ0μH=μ0(H+M)和式(8)得:

Aharoni 和Prozorov 通过数值计算的方法[22-23]分别给出了长方形磁体退磁因子跟形状尺寸的近似公式,如式(10)所示:
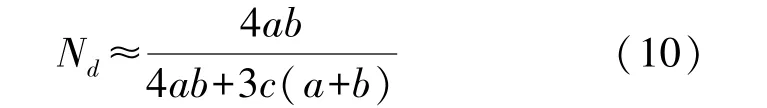
式中:c为磁体的长度,a、b分别为磁体的厚度和宽度所示。 实际应用中,a、b比c小一个数量级,所以式(10)分母中的4ab可忽略,并假设b=γa,即宽度为厚度的γ倍,可得:

由式(11)可知退磁因子的大小与磁体的长度成反比,当磁体截面积的宽度和厚度呈一定的比例关系时,与厚度和长度的比值成正比。 Chen 等[24]不仅考虑了磁体形状尺寸对退磁因子的影响,还研究了磁导率对磁体退磁因子的影响,即磁导率越大时退磁因子越小,通过查表的方式获得退磁因子的近似值。
作为对比研究,使用Maxwell 电磁仿真软件对FeGa 合金的磁化特性进行仿真,以计算退磁因子。设计FeGa 合金的尺寸为10.6 mm×1.4 mm×0.6 mm、20 mm×1.4 mm×0.6 mm、30 mm×1.4 mm×0.6 mm,仿真取FeGa 合金得相对磁导率为120,施加150 Oe 的均匀磁场,得到不同长度FeGa 合金内部磁感应强度沿长度方向的分布曲线如图2 所示,可以看出,由于退磁场的作用,虽然外加磁场是均匀的,FeGa 合金内部的实际磁感应强度分布并不均匀,呈两端磁感应强度小、中间磁感应强度大的分布趋势,与退磁场两端大中间小的分布趋势对应。 将内部磁感应强度B、μ=120 及Hext=150 Oe 代入式(9),得到不同尺寸FeGa 的退磁因子如表2 所示。
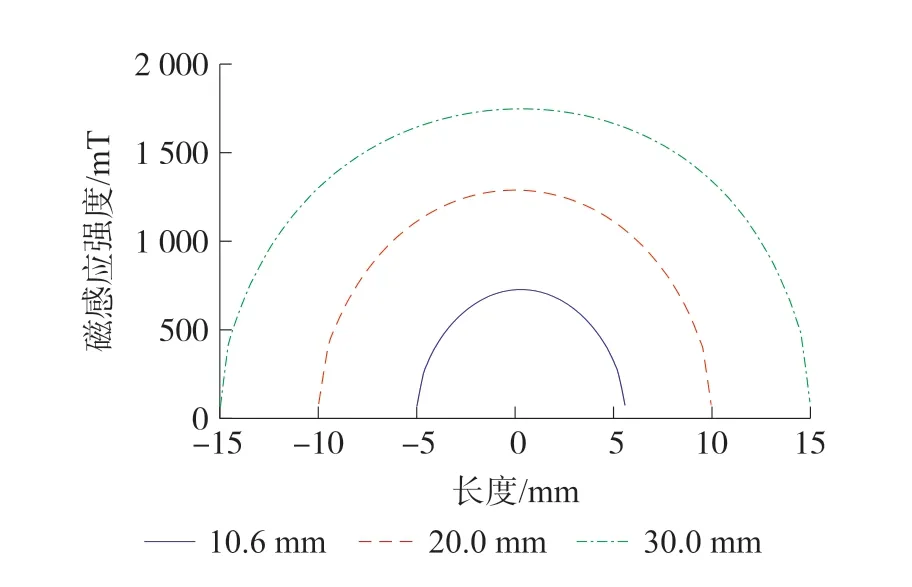
图2 不同尺寸FeGa 合金内部磁感应强度沿长度方向的分布

表2 仿真参数与仿真结果
考虑退磁场对不同长度FeGa 合金内部有效磁场的影响,将厂家提供的FeGa 合金材料参数:Em=107 GPa、λS=280×10-6、χm=177 及Ms=1.45×106A/m代入式(3),结合式(8),得到磁致伸缩系数和压磁系数随磁场变化的曲线,如图3 所示。 可以看出,对于长度越长的FeGa 合金,退磁因子越小,磁致伸缩系数随磁场增大越快、曲线越陡峭,即压磁系数越大,并且压磁系数取得最大值时所需的磁场越小。对于10.6 mm 长的FeGa 合金,压磁系数在230 Oe时取得最大值0.73×10-6/Oe,磁致伸缩系数线性区范围约为150 Oe~320 Oe;对于20 mm 长的FeGa 合金,压磁系数在120 Oe 时取得最大值1.16×10-6/Oe,磁致伸缩系数线性区范围约为80 Oe ~200 Oe;对于30 mm 长的FeGa 合金,压磁系数在65 Oe 时取得最大值1.64×10-6/Oe,磁致伸缩系数线性区范围约为40 Oe~110 Oe。

图3 不同尺寸FeGa 合金的磁致伸缩系数和压磁系数随磁场变化曲线
在理想情况下β=1,即音叉应变等于FeGa 合金产生的应变,联立式(5)、式(6)和式(8),得到不同长度磁致伸缩单元的传感器输出频率及灵敏度随磁场变化曲线,如图4 所示。 可以看出,退磁因子越小(即长度越长),频率随磁场增大越快、曲线越陡峭,即灵敏度越大,并且灵敏度取得最大值时所需的磁场越小,对应地,当退磁因子越小,磁敏感单元的线性工作区范围越小。 对于10.6 mm 长的磁敏感单元,传感器在230 Oe 时灵敏度取得最大值4.2 Hz/Oe,线性区范围约为150 Oe ~320 Oe;对于20 mm 长的磁敏感单元,传感器在120 Oe 时的灵敏度取得最大值6.7 Hz/Oe,响应线性区范围约为80 Oe~200 Oe;对于30 mm 长的磁敏感单元,传感器在65 Oe时的灵敏度取得最大值9.5 Hz/Oe,响应线性区范围约为40 Oe~110 Oe。
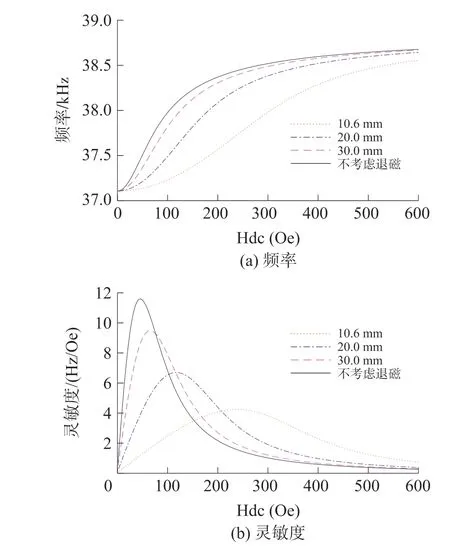
图4 不同尺寸磁敏感单元频率和灵敏度对磁场的理论响应曲线
3 器件制备及实验
首先准备好传感器制备所需的各个元件,主要包含:①通过光刻、湿法蚀刻等工艺在Z 切型石英晶体基片上制备的石英音叉谐振器,制作过程与文献[16]类似;②从Z 切型石英片上切下尺寸为1.8 mm×1.4 mm×0.1 mm 的垫片;③采用线切割工艺从定向凝固制备的FeGa 合金块体中切割出FeGa合金片,并对表面进行磨抛处理。 因为所用石英音叉谐振器的长度为10.6 mm、宽度为1.4 mm,厚度为0.1 mm, 因 此FeGa 合 金 的 最 短 长 度 取 值 为10.6 mm,较长的长度设计为20 mm 和30 mm,宽度相同为1.4 mm,为了获得较大的驱动力,FeGa 合金的厚度取值0.6 mm,为被驱动石英音叉谐振器厚度的6 倍。 在这样的配置下,退磁因子分别为0.018、0.007、0.002,呈现较大的变化梯度。
对各组成部件清洗、烘干后,通过环氧树脂胶将两个石英垫片分别粘贴在距FeGa 合金片中心5.3 mm 处(中心对称,石英垫片距10.6 mm、20 mm、30 mm 长度的FeGa 合金片两端距离分别为0 mm、4.7 mm、9.7 mm),之后放入烤箱中,缓慢升温至60 ℃后恒温烘烤1 h,然后缓慢降至室温取出;再通过环氧树脂胶将音叉固定端粘接在石英垫片上制成不同尺寸的复合谐振式磁敏感单元,再放入烤箱升至60 ℃保温1 h 后取出,得到如图5(a)所示的不同尺寸的磁传感器敏感元件。 带振荡电路的磁传感器敏感元件如图5(b)所示。

图5 不同尺寸的磁传感器敏感元件和带振荡电路的磁传感器敏感元件
谐振式磁传感器性能测试系统如图6 所示,主要由亥姆霍兹线圈、F2030 程控电流源(北京乐真科技有限公司,60 V、10 A)、HSPY600 稳压源、振荡电路、Agilent53210A 频率计组成。 程控电流源输出电流驱动转换系数为28 Oe/A 的亥姆霍兹线圈产生磁场,HSPY600 稳压源给振荡电路供电,振荡电路输出信号的频率值由Agilent53210A 频率计测量,采用Labview 编制程序实现电流源输出电流控制和频率计数据读取。 测试时,首先控制电流源输出电流按照从0→10 A→0→-10 A→0 的规律变化,测得±280 Oe 磁场范围内谐振频率随磁场变化的曲线。传感器的灵敏度是谐振频率对磁场的一阶导数,通过测试曲线差分计算获得。
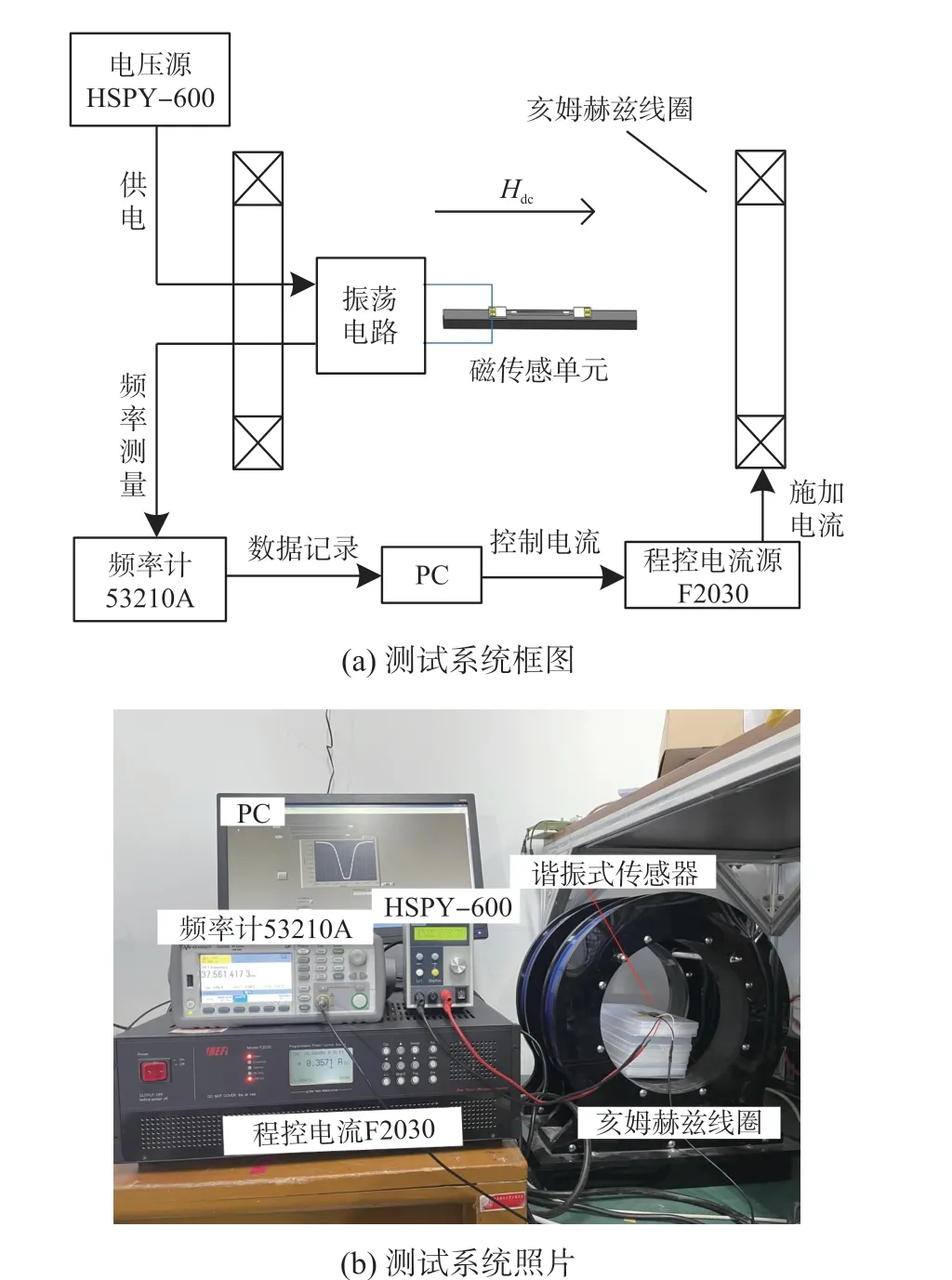
图6 谐振式磁传感器性能测试系统
4 结果及讨论
首先采用示波器观测门振荡电路输出的波形,如图7 所示。 基于音叉谐振器的门振荡电路能输出稳定的方波信号,其频率值为37.34 kHz,主要取决于音叉谐振器的谐振频率。
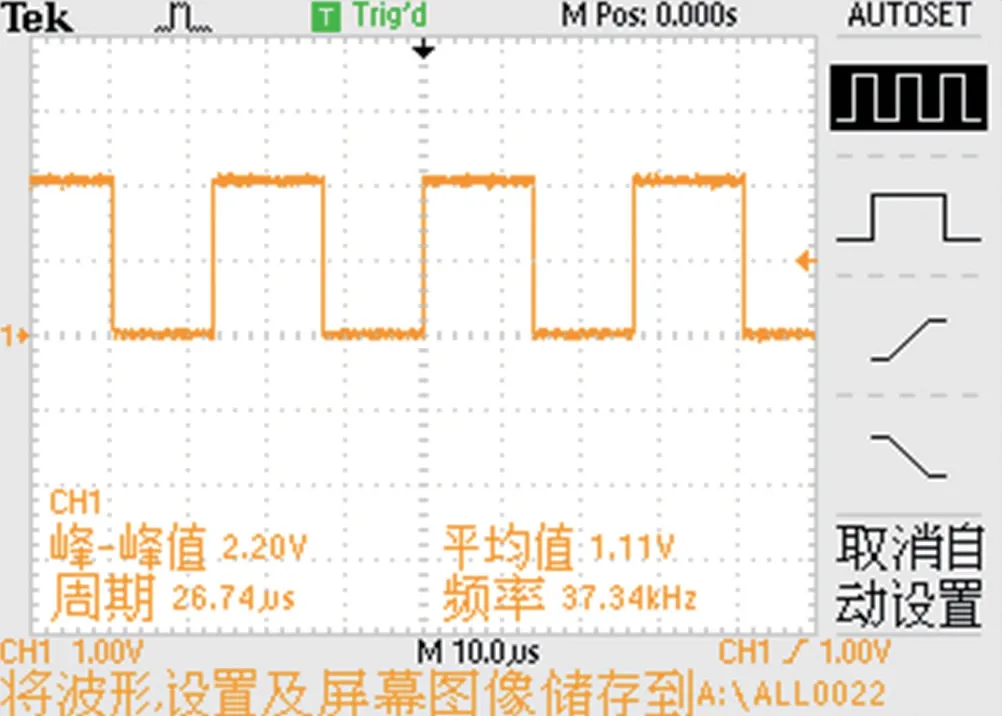
图7 门振荡电路输出方波信号
其次,测得不同长度的谐振磁传感器的谐振频率随偏置磁场变化曲线,如图8(a)所示,测试范围为±280 Oe,间隔为10 Oe;进一步计算得到传感器灵敏度随偏置磁场变化曲线,如图8(b)所示。 可以观察到,磁场较小时,谐振频率随磁场变化缓慢;磁场进一步增大时,谐振频率随磁场变化的灵敏度增加,并且逐渐呈较佳的线性变化;磁场进一步增大时,变化再次变缓,该过程与磁致伸缩系数随磁场变化特性相吻合,这是因为在低磁场时磁场导致的是磁畴壁缓慢增大的变化,磁场进一步增大时发生的是磁畴旋转运动,而大磁场下逐渐趋于饱和磁化。对于尺寸为10.6 mm×1.4 mm×0.6 mm 的FeGa 合金片,其退磁因子为0.018,退磁场对灵敏度的影响最大,仅为3.7 Hz/Oe,灵敏度取得最大值时的磁场最大,为230 Oe,谐振频率随磁场变化的线性工作区约为90 Oe~260 Oe;对于尺寸为20 mm×1.4 mm×0.6 mm 的FeGa 合金片,其退磁因子为0.007,此时灵敏度增加到5.8 Hz/Oe,退磁场对灵敏度的影响更小,灵敏度取得最大值时的磁场也变小,为150 Oe,谐振频率随磁场变化的线性工作区为70 Oe ~190 Oe;对于尺寸30 mm×1.4 mm×0.6 mm 的FeGa合金片,其退磁因子为0.002,此时退磁场的影响最小,灵敏度为9 Hz/Oe,并且灵敏度取得最大值时的磁场最小,为60 Oe,谐振频率随磁场变化的线性工作区为变为30 Oe ~90 Oe。 可以看出长度越长(即退磁因子越小)时,退磁场的影响越小,灵敏度越大,并且灵敏度取得最大值时所需的磁场越小,实验结果与理论结果较吻合。 从图4(a)仿真的结果看,30 mm 长度的磁致伸缩系数曲线已经较为接近不考虑退磁影响的磁致伸缩系数曲线,继续增加长度降低退磁带来的好处有限,因为传感器的小尺寸也是考虑的重要因素。 从实验的结果看,退磁因子为0.002 时可以得到较好的灵敏度增强效果,后续的研究考虑尽量缩短磁致伸缩材料的长度,优化长度和厚度之间的关系,使得在维持一定厚度以维持足够驱动力的前提下,退磁因子仍然保持在0.002 左右。
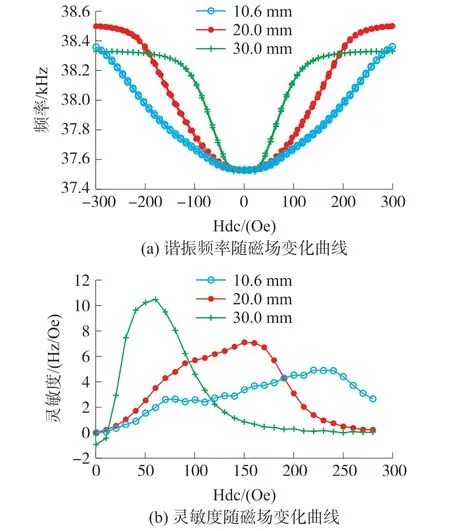
图8 不同尺寸的磁传感器实验测试曲线

表3 不同尺寸的磁传感器实验数据
5 小结
研究了退磁场对FeGa 磁致伸缩应力耦合谐振磁传感器灵敏度的影响。 由于FeGa 合金在磁化过程中会产生与外加磁场方向相反的退磁场,FeGa 合金内部的有效磁场小于外加磁场,减小的磁场大小即退磁场大小,与磁体的磁化强度、磁导率及尺寸比有关。基于Z-L 模型建立磁致伸缩FeGa 合金的非线性模型,结合退磁因子计算经验公式与Maxwell 电磁仿真分析不同尺寸FeGa 合金的退磁因子,分析并预测了退磁场对磁传感器灵敏度的影响,发现传感器灵敏度随FeGa 合金长度的增加而增加,最优偏置点的灵敏度分别为3.7 Hz/Oe(L= 10.6 mm,退磁因子为0.018)、5.8 Hz/Oe(L=20 mm,退磁因子为0.007)和9 Hz/Oe(L=30 mm,退磁因子为0.002)。 制备不同长度磁敏感单元的实验结果和理论分析结果较为吻合。 虽然增加磁致伸缩敏感材料的长度可以提高传感器的灵敏度,但是FeGa 长度的增加也带来了传感器体积的增加。 本文的研究结论为后续提高传感器灵敏度并缩短磁致伸缩单元长度,优化传感器尺寸提供了思路。

