基于样本迁移的在线脑电分类方法*
李震宇,佘青山,马玉良,张建海,孙明旭
(1.杭州电子科技大学圣光机联合学院,浙江 杭州 310018;2.杭州电子科技大学自动化学院(人工智能学院),浙江 杭州 310018;3.浙江省脑机协同智能重点实验室,浙江 杭州 310018;4.济南大学自动化与电气工程学院,山东 济南 250022)
脑机接口(Brain-Computer Interface,BCI)是在人与计算机或其他电子设备之间建立的不依赖于常规大脑信息输出通路(外周神经和肌肉组织)的一种通讯和控制技术。 脑电信号(Electroencephalogram,EEG)是BCI 系统中最常用的输入信号,具有高时间分辨率、低成本、高便携性等优势,因此被广泛用于辅具控制、医疗康复、车辆驾驶,日常生活娱乐等领域[1-3]。
由于脑电信号的非平稳性和个体差异性[4],在面对不同的受试者、设备和不同的任务时,很难建立一个最优的通用机器学习模型。 对于新受试者,模型通常都需要较长时间训练,这个过程既耗时又费力[5]。 迁移学习(Transfer Learning,TL)是减少训练时间的重要方法之一,利用不同领域以及相关任务的相似性把其他受试者的知识迁移到目标受试者的任务上,来帮助目标受试者训练分类模型。 迁移学习不仅能够有效利用己有数据来提高数据的复用性,还能减少不同受试者的个体差异。 现在许多研究者已经将迁移学习成功应用于脑电信号识别中,并取得了令人印象深刻的成果。 文献[6]提出了迁移半监督宽度学习(Semi-Supervised Broad Learning System with Transfer Learning,TSS-BLS)方法,利用迁移学习使标记和未标记样本的分布尽可能一致,来降低未标记样本的风险从而提高半监督算法的安全性。 文献[7]提出一种子带目标对齐共空间模式(Sub-Band Target Alignment Common Spatial Pattern,SBTACSP)方法,将子带滤波与迁移学习相结合,提高从子带中获取频率信息的能力,进一步提高了分类精度。
大多数迁移学习方法通常在离线环境下以批量式学习的方式进行,所使用的训练和测试样本都是预先给定的[8-9]。 然而,这种一次性收集到足够的训练样本的方式在实际应用中可能不适用;另外,在某些情况下,需要按顺序接收测试样本。 而在线学习保留了历史信息,从而避免了从头开始重复的批量训练,显著减少了计算量;在线学习还能通过适应数据动态产生最新模型,使其能够处理非平稳问题。在线学习已被广泛研究多年,一些在线算法如在线支持向量机(Support Vector Machine,SVM)[10]、被动攻击(Passive-Aggressive,PA)算法[11-12]等也在BCI中得到应用,具体实例如可穿戴导航系统[13]和基于头戴式设备的增强现实(Augmented Reality,AR)系统[14]等。 然而,现有的在线学习算法也存在一些不足,如PA 只保持固定的权重,无法准确地应用在其他应用场景或领域;还有一些在线算法通常将所有错误分类的样本存储为支持向量(SV),这可能会导致计算和内存成本过高,尽管可以通过一些算法将存储的SV 数目设定为低于特定阈值[15],但大多数在线学习算法仅利用一阶信息并为所有特征分配相同的学习率,这可能会导致收敛速度缓慢。
最近,在线迁移学习(Online Transfer Learning,OTL)[16]将在线学习动态更新分类模型与迁移学习能够有效利用源域知识的优点相结合,提前收集有标记的源域数据,并以在线方式分多轮接收目标域数据,每轮只接收一个目标样本。 现有的在线迁移学习方法侧重于利用源领域的知识在目标领域进行在线学习。 文献[17]采用基于集成学习的策略,利用源域数据训练分类器,通过不断调整组合权值使分类器适应新的数据。 文献[18]提出多类分类在线迁移学习算法(Online Transfer Learning Algorithm for Multi-class Classification,OTLAMC),设计了新的损失函数和更新方法,将二分类的在线迁移学习拓展至多类当中。 文献[19]提出了一种多源在线迁移学习算法(Online Transfer Learning with Multiple Sources,OTLMS),通过自适应源域选择方法,在OTL 过程中迁移多个源域知识。 文献[20]提出了一种在线分布差异最小化的同构在线迁移学习(Homogeneous Online Transfer Learning with Online Distribution Discrepancy Minimization, HomOTLODDM)算法,用于减少多个域之间的边缘分布和条件分布差异。
BCI 技术的最终目的是在线应用,离线应用是验证信号的处理和分析算法,在线应用则需要在准确识别的同时,满足对算法的实时性和稳定性要求。针对在线BCI 系统对实时性的要求,应减少算法的计算复杂度和单次识别时处理数据的大小,本文提出了基于样本迁移的在线脑电分类方法,对跨被试者的运动想象脑电数据进行在线建模分类。 首先,对脑电数据进行欧式空间对齐预处理,提取公共空间模式特征,并完成离线分类器训练。 其次,对单个样本进行在线欧式空间对齐,更新整个样本空间的协方差矩阵后再提取CSP 特征,并将在线分类器与离线分类器进行组合来对标签进行预测。 同时,通过真实标签计算损失函数来更新在线分类器和分类器的权重。 最后,本文分别利用BCI 竞赛Ⅳ-Ⅰ和Ⅳ-Ⅱa 的数据集对该方法进行了测试,并与几种同类型方法进行比较和分析,以验证所提方法的有效性。
1 方法
1.1 欧式空间对齐
欧式空间对齐[21](Euclidean Space Data Alignment,EA)是一种底层的迁移学习算法。 EA 在原理上是将不同用户的平均协方差矩阵都对齐到单位矩阵,从而减少域间分布差异。 EA 对齐的对象是原始样本而非协方差矩阵,且不改变原始样本的维度。
对于离线的训练数据,假设输入样本为X∈Rn×D,其中n为样本个数,D为每个样本的特征维度。 那么,可计算其协方差矩阵的算术平均值为:

然后样本通过如下变换:

校准后,所有n个校准试验的平均协方差矩阵为:

当对所有受试者执行上述变换后,它们的平均协方差矩阵都会变成单位矩阵。 因此不同受试者的协方差矩阵的分布更为相似,而样本协方差矩阵是EEG 信号的一个重要统计量,受试者间的个体差异也会变小。
EA 作为一种预处理方式能够有效地减小个体差异,降低错误分类的风险。 在EA 对齐之后,可以使用传统机器学习算法进行分类。
1.2 公共空间模式算法
公共空间模式[22](Common spatial pattern,CSP)是一种有效的特征提取方法,被广泛应用于脑电分类。 其基本思想是学习空间滤波器,使一类带通滤波后的脑电信号方差最大,而另一类带通滤波后的脑电信号方差最小,从而得到差异最大的特征。 给定一条N通道的时空脑电信号X,其中X是一个N×T矩阵,T表示每个通道的样本数。 EEG 的归一化协方差矩阵如下所示:
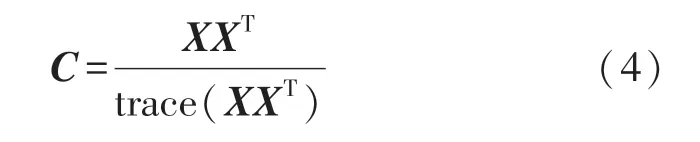
每个类别的协方差矩阵C1和C2,可以通过样本均值来计算。 CSP 的投影矩阵是:

式中:U是正交矩阵,P是白化特征矩阵。 经过投影矩阵Wcsp滤波后,可得特征矩阵:

取特征矩阵的前m行和后m行构建矩阵Z=(z1z2…z2m)∈RN×2m,进行归一化处理后可得到特征向量F=(f1f2…f2m)T∈R2m×1。
1.3 同构在线迁移学习
在同构在线迁移学习[17](Homogeneous Online Transfer Learning,HomOTL)研究中,源域和目标域共享相同的特征空间,定义源域空间为Xs×Ys,其中Xs=Rm,Ys={-1,+1},HomOTL 任务的目标是从目标域空间X×Y中的一系列样本{(xk,yk)|k=1,…,K}中在线学习目标域上的预测函数f(xk)。
在不损失一般性的前提下,假设预测函数采用线性预测模型,即f(xk)= sign(wTk xk)。 具体来说,在线学习任务的第k轮实验中,收到一个样本xk,在

HomOTL 解决方案的基本思想是基于集成学习策略。 首先以离线方式用源域中的数据构造预测函数v,以在线方式仅用目标域中的数据构造一个全新的预测函数w,然后学习一个融合了预测函数v和w的集成预测函数,从而可以从源域迁移知识。
1.4 本文方法
本文提出一种基于样本迁移的在线脑电分类方法(Online EEG Classification based on Instance Transfer,OECIT),其框架如图1 所示。
对于源域中的所有受试者脑电数据,利用EA和CSP 分别对训练数据和测试数据进行预对齐以及特征提取,训练得到离线分类器。 在线过程中不断引入新的样本,并在执行在线预对齐和CSP 后,用所提取特征训练在线分类器。 在线分类器和离线分类器结合后,对样本进行预测分类,并与真实标签进行比较,从而不断更新在线分类器以及分类器权重,之后通过不同的权重将两个分类器结合,来预测标签信息。
首先,本文对基于离线的欧式空间方法进行改进,提出一种在线欧式空间对齐算法(Online Euclidean Space Data Alignment,OEA),目的在于能够通过在线的方式来对EEG 数据进行预对齐。 对于在线的测试数据,假设目标域一共有K个样本,为{(xk,yk)|k=1,…,K}。 在第k轮,有样本(xk,yk)输入,目标域信号矩阵更新为:

求取其协方差矩阵的算数平均值为:

式中:nk为第k轮样本总数,Xk,i为第k轮第i次目标域信号矩阵,¯Ek为第k轮目标域样本欧几里得均值,对目标域空间进行如下变换:

式中:Xk为第k轮的目标域信号矩阵,~Xk为第k轮对齐后的目标域信号矩阵。 每次样本的加入,会使协方差矩阵的算术平均值更新,通过每一轮样本进行变换,使测试数据的协方差矩阵的分布越来越相近。
本文将OEA 与HomOTL 的两种算法结合,提出以下两种在线的脑电分类算法:
①OECIT-Ⅰ
为了于在线学习任务的第k轮中有效地组合两个预测函数v和wk,同质在线迁移算法HomOTL-Ⅰ分别为这两个预测函数引入了两个组合加权参数α1,k和α2,k。 在第k步,给定一个样本xk,通过式(8)和式(9)对其进行OEA 处理后,再使用CSP 提取特征~xk,并通过以下预测函数预测其类标签:


算法1 OECIT-Ⅰ

接收真实标签:yk={-1,+1}计算下一轮的权重:α1,k+1= α1,ksk(v)α1,ksk(v)+α2,ksk(wk),α2,k+1= α2,ksk(wk)α1,ksk(v)+α2,ksk(wk)计算损失函数:ℓk=[1-ykwTk~xk]+if ℓk>0 then wk+1=wk+τkyk~xk,其中τk=min{C,ℓk/‖~xk‖2}end if end for
②OECIT-Ⅱ
HomOTL-Ⅱ为错误驱动算法,与HomOTL-Ⅰ相比,除了引入了两个组合加权参数α1,k和α2,k外,还增加了权重参数θ1,k和θ2,k。 在第k步,给定一个样本xk,在OEA 预处理和特征提取后,得到特征~xk,通过以下预测函数预测其类标签:

式中:β∈(0,1)是一个折扣权重参数,初始化θ1,1=θ2,1=1 用于惩罚在每个学习步骤执行错误预测的分类器,Zi,k=Ⅱ(ykvT~xk≤0)表示相应的分类器对样本特征~xk的预测是否出错,如果括号内的条件成立,则等于1,否则为0。 算法2 总结了所提出的OECIT-Ⅱ算法。

算法2 OECIT-Ⅱ

if ℓk>0 then wk+1=wk+τkyk~xk,其中τk=min{C,ℓk/‖~xk‖2}end if α1,k=θi,k Θk其中i=1,2,Θk=∑2 i=1θi,k end for
2 实验
2.1 数据描述
本文采用的数据集来自于“BCI Competition IV”中的公开数据集[23],包括数Dataset Ⅰ和DatasetⅡa。 下面对两个数据集进行简单介绍。
①MI1:DatasetⅠ
数据集由7 名健康受试者的脑电数据组成。 每个受试者的数据由受试者的左手、右手和脚三个类别中选择两个类别运动想象的脑电图组成,每类有100 次试验。 每次实验信号均使用59 个电极进行记录,电极位置采用国际10/20 系统。 59 个通道的EEG 信号被记录并以100 Hz 采样。
②MI2:Dataset Ⅱa
数据集由9 名健康受试者的脑电数据组成。 每个受试者的数据由一个受试者的左手、右手、脚和舌头四类运动想象的脑电图组成,每类有72 次试验。每次实验信号均使用25 个电极进行记录,电极位置采用国际10/20 系统。 22 个通道的EEG 信号和3个通道的EOG 信号被记录并以250 Hz 采样。 本文主要选取左手和右手的22 通道EEG 数据。
2 个数据集的实验过程类似,任务开始时,屏幕会出现正十字符号“+”,提示用户做好准备。 2 s~6 s之间会在正十字符号“+”上叠加一个方向的箭头,对应受试者需要完成的运动想象任务。 之后2 s 黑屏,用户可以休息。
2.2 数据预处理
本文采用MATLAB 中的EEGLAB 工具箱来对数据集进行预处理。 首先使用带通滤波器在[8,30] Hz 的频率滤波,以去除肌肉伪迹,噪音污染等。之后提取动作提示箭头出现后的[0.5,3.5] s 之间的EEG 信号,作为数据集样本。
3 实验结果及分析
本节使用运动想象数据集Ⅰ和Ⅱa 来测试OECIT-Ⅰ和OECIT-算法的性能,并将之与几种同类型方法进行比较。 在联想Lenovo G50-70M 笔记本上执行实验测试,具体配置为Intel Core i5-4258U CPU@ 2.40GHz,8GB 内存,512GB 固态硬盘,运行64 位windows 10 专业版以及MATLAB 2018b。
对每一个数据集,采用留一法确定目标受试者和源受试者,即每次试验选取一个受试者作为目标受试者,其他为源受试者,直到所有受试者都经过一轮选择。 实验开始时,只有源受试者的数据,而没有目标受试者数据,利用源受试者的数据先构建离线模型。为了模拟在线过程,对于目标受试者的数据进行20次随机排列,进行20 次在线测试,最终取20 次结果的平均值。 在实验过程中,不断获得目标受试者的已标记样本,然后通过这些已标记样本不断更新在线模型,并将其用于接下来的目标受试者样本预测。
在本文实验中,用于比较的几种算法包括:
①基准算法PAIO[24]:旧分类器初始化被动攻击算法(PA Initialized with the Old classifier,PAIO)为在线算法PA 算法的变体,这是一种没有使用预对齐和源域知识的算法。
②EA-CSP-LDA[21]:预对齐的迁移方法,先使用EA 对齐不同受试者,再进行CSP 滤波,最后使用的是LDA 分类器。
③CA-JDA[25]:以协方差矩阵质心对齐作为预处理步骤,减少不同域的边际概率分布偏移,并实现从多个源域的转移。
④RA-MDRM[26]:一种黎曼空间方法,将协方差矩阵相对于参考协方差矩阵居中。
⑤OECIT-Ⅰ:在线预对齐算法OEA 结合同质在线迁移算法HomOTL-Ⅰ。
⑥OECIT-Ⅱ:在线预对齐算法OEA 结合同质在线迁移算法HomOTL-Ⅱ。

表1 和表2 给出了不同算法在两个数据集的性能表现,对两个数据集共16 名受试者,CA-JDA 算法的表现最差,其次是RA-MDRM,表现最好的是EACSP-LDA,这表明EA 算法更适合用于在线预对齐处理。 EA+CSP+LDA 的迁移方法要优于基准算法PAIO,但分类结果并没有取得最好的性能,这说明了开发在线更新分类器的重要性。 通过结合同质在线迁移算法提出了OECIT-Ⅰ和OECIT-Ⅱ算法,OECIT-Ⅱ算法与OECIT-Ⅰ算法相比,改变了权重更新和标签预测方法,拥有更高的在线分类精度,并在大部分受试者中都获得了最好的性能,说明OECIT-Ⅱ权值更新方法在脑电数据在线分类中能更够有效地迁移源域知识。 在所有算法中OECIT-Ⅱ算法的平均准确率最高,这意味着通过结合在线预对齐和在线迁移学习算法,能够提高迁移学习算法的在线分类性能。

表1 MI1 数据集上的在线分类准确率比较

表2 MI2 数据集上的在线分类准确率比较
表3 比较了几种算法在计算耗费时间上的差异,可以观察到,RA-MDRM 和CA-JDA 算法耗时都过长,PAIO 作为在线算法耗时最少。 OECIT 因为增加了在线预处理的步骤,耗时比PAIO 要多;而相较于EA-CSP-LDA 算法,OECIT 要快1.27 ~1.37 倍,且不同数据集上耗时的方差更小。

表3 不同算法的分类耗时比对
图2 和图3 是对MI1 和MI2 的数据集进行样本分析的结果,分别显示出了每种算法在目标受试者上的学习过程中平均正确率变化的细节,误差线表示正确率的标准差。 由于一开始进入样本数量较少,存在标准差较大的情况,随着样本数不断增加,标准差会越来越小。 在两个数据集共16 名受试者中,OECIT-Ⅰ和OECIT-Ⅱ在14 名受试者上的平均准确率变化都比EA-CSP-LDA 更好,说明带有加权更新策略的算法更适合进行在线分类。 相似的观察结果表明,这两种算法在接收到少量的样本(例如少于100 个样本)后性能最好,这意味着这两种算法所采用的策略可以有效地将所学知识从源域迁移到目标域,再次验证了OECIT 方法的高学习效率。

图2 MI1 数据集上在线分类准确率随样本数量变化曲线
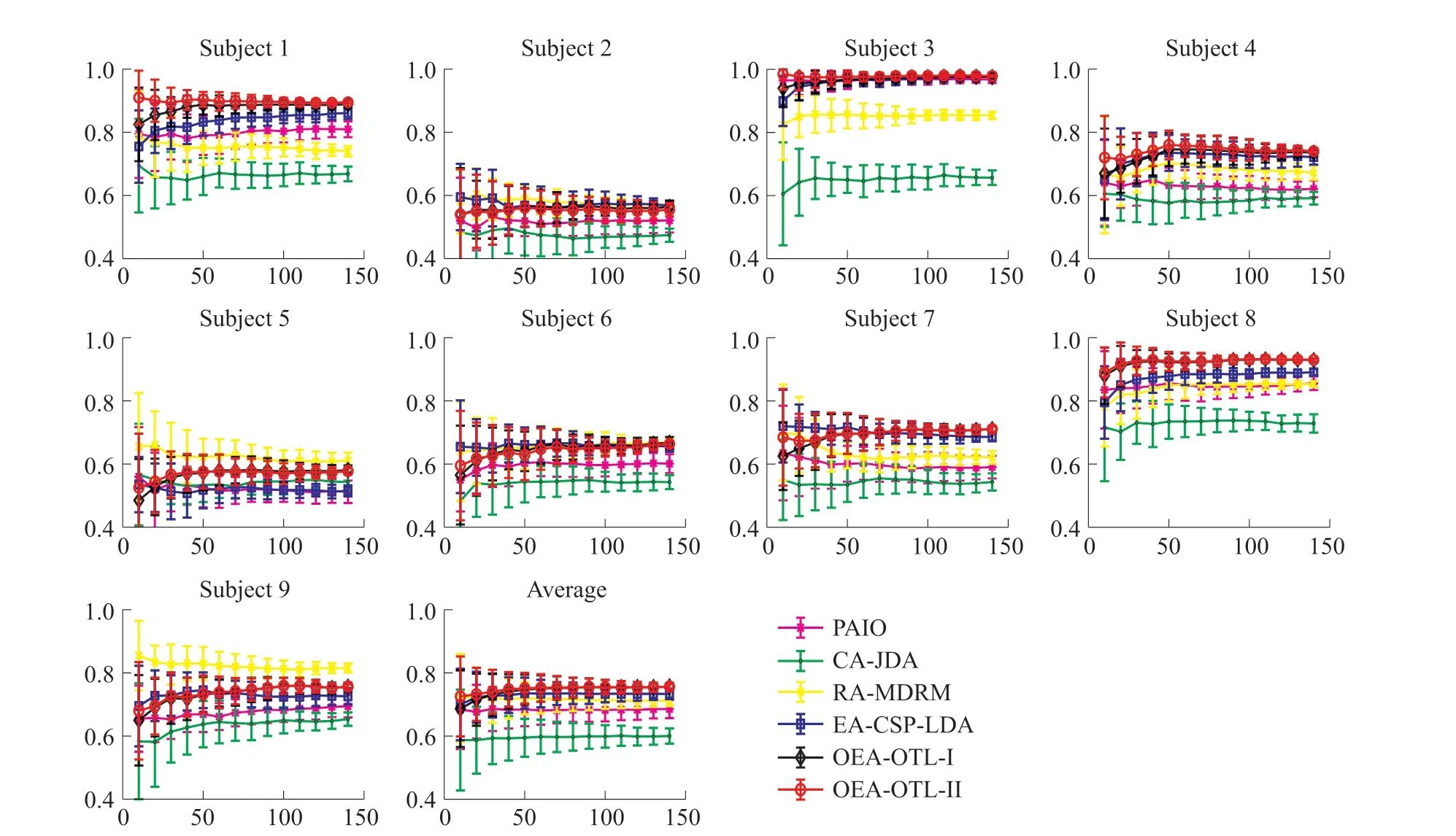
图3 MI2 数据集上在线分类准确率随样本数量变化曲线
4 结论
本文提出一种基于样本迁移的在线脑电分类方法,首先通过离线方式对训练数据进行EA 和CSP处理得到特征来训练离线分类器,其次以在线方式将测试数据分成许多样本,每次只加入一个样本进行OEA 和CSP 特征提取,用于训练在线分类器,然后将离线分类器与在线分类器进行加权组合,来进行标签预测。 OEA 能够很好地消除由于个体差异而造成的负迁移,而在线迁移的权值更新策略能够有效地迁移源域知识。 在两个公开数据集上的实验结果表明,在线分类场景应用下,本文方法的分类性能要优于现有基准方法。 本文所做工作验证了在线迁移学习应用于运动想象脑电信号识别的有效性,可为脑机接口在线系统提供方法参考。

