不同密度粉质粘土K0固结侧向卸荷三轴试验研究

吴 昳，朱俊高*，黄浩然，褚福永

(1.河海大学 岩土力学与堤坝工程教育部重点实验室，江苏 南京 210098；2.河海大学 岩土工程科学研究所， 江苏 南京 210098；3.浙江省水利水电勘测设计院，浙江 杭州 310002；4.丽水学院 工学院，浙江 丽水 323000)

近年来城市地下空间开发迅猛，基坑的开挖范围及深度逐渐增大，基坑设计的安全稳定性也因此受到更多人的关注。在基坑工程中，支护结构后的土体荷载作用方式与一般的加载不同，即为侧向卸荷。众所周知，应力路径的不同会对土体的强度、变形造成很大的影响[1-4]，利用有限元等数值方法对基坑等侧向卸荷的土工结构进行应力变形分析时，能否考虑卸荷这种特殊路径下土体的应力应变特性对其变形及稳定性预测的准确性有着重大影响[5]。本构模型的深入研究以及现有本构模型的验证也依赖于更多的类似侧向卸荷等特殊应力路径下试验成果。因此，研究土体在侧向卸荷路径下的强度与变形特性具有重要意义[6]。

对于基坑工程中土体在侧向卸荷应力路径下的应力应变及强度特性，前人已经进行了大量的研究。曾国熙[7]等认为开挖时土体可分为两个区域：主动区域与被动区域。刘国彬[8]以某粉质粘土为例，进行了不同路径下的室内加荷以及卸荷试验。并推导出了侧向卸荷路径下的模量公式，公式显示固结压力和应力路径对其结果影响较大。刘熙媛[9]等研究发现侧向卸荷的土体抗剪强度远低于常规三轴试验。殷德顺[10]进行了侧向卸荷、加荷的应力路径三轴试验，提出了相应的模量公式，验证表明该公式能够更好地模拟基坑问题。张玉等[11]用真三轴仪对黄土进行了侧向卸荷探究，发现侧向卸荷条件下土体破坏时的应变远小于竖向加载和常规三轴试验。以上学者的研究成果为基坑工程设计提供了重要参考。但目前针对侧向卸荷条件下土体变形特性规律的研究还很不充分。比如，上述研究一般都是基于各向等压固结的常规三轴剪切试验结果[12]。事实上，地基开挖前一般是处于无侧向变形的K0固结状态[13-14]，而且，开挖时基坑支护后面的填土经历的是侧向卸荷，与常规三轴剪切的应力路径相差甚远。因此，进行等压固结的三轴试验，即使考虑卸荷，也与实际情况有误差。有必要弄清楚K0固结后侧向卸荷条件下土体应力应变及强度的特性。从而，为更科学合理地建立比较完善的本构模型、进行基坑受力变形准确分析提供基础。再如，现有本构模型基本都是基于常规三轴压缩试验建立[15-18]，这些模型反映诸如侧向卸荷等特殊应力路径下的应力应变关系能力有限，有时甚至很差。它们对侧向卸荷路径的适用性并没有得到充分验证，需要更多、更接近实际应力路径的试验来验证，并进一步总结相关应力应变规律。为此，本文针对某粉质粘土，利用应力控制式三轴剪切仪，进行K0固结下的侧向卸荷三轴固结排水剪试验，研究不同干密度粉质粘土侧向卸荷路径下土体的强度特性以及变形特性，并进一步总结密度对强度、侧向应变的影响规律。

1 试验土料与试验方案

试验土样采用南京浦口区滨江大道某段取得的粉质粘土，其基本物理性质指标见表1。经测定，该土料为低液限粉质粘土。

表1 试验土体的基本物理性质指标Tab.1 Basic physical property indexes of mixed soil

本文试验采用重塑样。将扰动土样采用人工压实方法制备成直径3.91 cm、高8 cm的三轴圆柱试样。

为研究基坑开挖过程中周围土体的应力应变关系及强度特性，对试样先进行K0固结试验，固结围压分别为50、100、200、300 kPa；固结完成后，进行轴向应力(大主应力)不变、围压减小的应力路径试验。

这里对三种不同干密度试样(1.27、1.45、1.57 g/cm3)进行试验，以便研究密度对试验结果的影响。具体试验方案见表2。

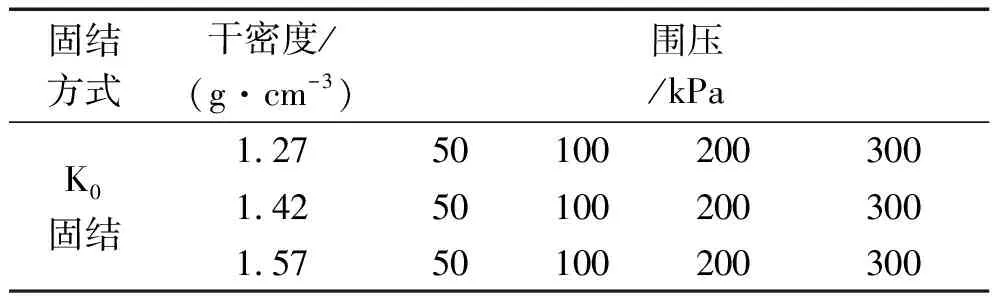
表2 试验方案Tab.2 Test program

2 试验结果分析

2.1 侧向卸荷路径下土体应力应变关系

依据表2的试验方案，进行了3种不同密度粉质粘土K0固结的侧向卸荷试验。侧向卸荷路径下试样的轴向应变和轴向附加应力，(σ1-σ3)-εa，关系曲线如图1所示。为便于分析干密度对试验结果的影响，将同一围压下不同干密度粉质粘土关系曲线绘制于同一幅图中。

2.2 强度特性对比分析

从图1可以看出，相同轴向应变和围压条件下，随着干密度的增加，轴向附加应力(σ1-σ3)均呈增大趋势，且随着干密度的增加，曲线的初始切线斜率显著变大，即试样的初始变形模量随干密度增大而增大。

图1 不同干密度(σ1-σ3)-εa曲线Fig.1 Relationship between (σ1-σ3) and εa of soils with different dry densities

为进一步探究密度对侧向卸荷路径下土体强度的影响，整理出土体破坏(即峰值强度或15%轴向应变)时对应的(σ1-σ3)与干密度的关系，绘制成曲线如图2所示。由图可知，相同围压下，随干密度的增大，试样剪切破坏时的(σ1-σ3)也略微增大。

图2 土样破坏时(σ1-σ3)随干密度ρd变化关系Fig.2 Relationship between (σ1-σ3) and dry density during soil sample failure

绘制土体的强度包络线,如图3所示。得出土体的强度参数并列于表3。从表3可以看出，随着干密度的增加，粘聚力看不出明显规律，内摩擦角则呈现出略微增大的趋势。

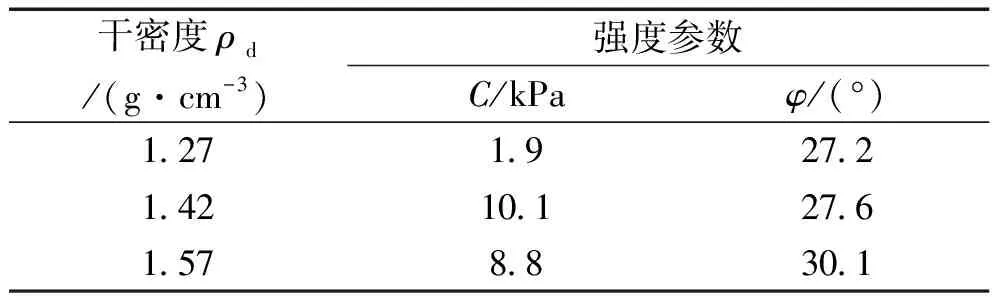
表3 试验土样抗剪强度指标Tab.3 Shear strength index of test soil samples

图3 不同密度试验强度包络线Fig.3 Intensity envelope plot of soils with different dry densities

为进一步研究干密度对强度的影响规律，在σ-τ坐标系中过原点分别作围压50、100、200、300 kPa时剪切破坏的莫尔圆切线，切线与横坐标夹角记为φs，该值具有摩擦角的概念，这里作者称之为“视摩擦角”。结果整理成表4。

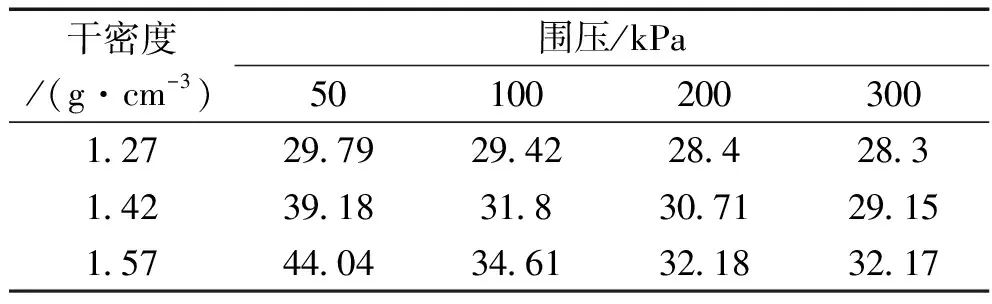
表4 各围压下的视摩擦角(单位：(°))Tab.4 Apparent friction angle under different confining pressures

由表4可以看出，相同围压下，视摩擦角随着干密度的增加而逐渐增加，较为直观地表明随着土体干密度的增加，抗剪强度逐渐增大，且近似成线性关系。为此，作者整理了不同围压下视摩擦角随干密度变化关系，并用直线拟合，如图4所示。

图4 不同围压下视摩擦角随干密度变化关系Fig.4 Relationship between apparent friction angle and dry density under different confining pressures

图4中拟合直线斜率的物理意义是干密度每增加1 g/cm3所增加的摩擦角值。为了方便应用，这里，将该斜率值除以10，以Δ表示，则Δ为干密度每增加0.1 g/cm3所增加的摩擦角。

整理Δ-σ3/Pa关系曲线，如图5所示。深入研究发现，Δ-σ3/Pa关系的试验数据点可以用式(1)很好拟合。

(1)

式中，α、β、δ为拟合参数，这里，其值分别为1.73、1.31和3.45。注意，应用此式时，干密度的单位为g/cm3，Δ单位为(°/0.1 g-1·cm-3)，且这些拟合参数的大小与土类有关。

图5 Δ-σ3/Pa关系试验点与拟合曲线比较Fig.5 Comparison of Δ-σ3/Pa relation curve between experimental results and fitting curve

式(1)有一定的实用价值，依据它就可以估计粉质粘土因干密度变化而引起的摩擦角的变化。比如，对某粉质黏土层，如果厚度较大，其干密度一般随埋深增大，此时，只要知道某埋深处的内摩擦角，而且知道压缩曲线或干密度随深度变化的规律，就可以用式(1)估算内摩擦角随深度变化的规律。可以使相关计算或设计更精细。

2.3 变形特性对比分析

为对比不同密度条件下试样的变形特性，将同一围压下不同干密度土体的体积应变与轴向应变(εv-εa)关系曲线绘制在图6中。从图6可以看出，随干密度增大，土样的剪胀性增强。以围压100 kPa为例，对干密度1.27 g/cm3的试验，破坏时体变约为0.25%，而干密度为1.57 g/cm3的试样，破坏时体变约为-1.5%。

图6显示，围压越低，土样发生相变(体积由压缩转为膨胀)对应的轴向应变越小。以干密度1.42 g/cm3的试样为例，在50 kPa围压下，轴向应变等于2%时就发生相变，而在100 kPa围压下，轴变到4%才发生相变。

为进一步分析不同干密度下试样破坏时的侧向变形规律，整理出各试样破坏时的侧向应变如表5所示。由表可看出，同一干密度下随着围压的增加，试样破坏时的侧向应变逐渐减小；而相同围压下，随着干密度的增加，试样破坏时的侧向应变增大。分析产生原因，与剪胀性有关。由前文已知，干密度越大，土体的剪胀性越明显，再加上实验时附加轴向应力逐渐增大，侧向却在卸荷、解除约束，土体颗粒便会向两侧移动，增大侧向应变。

表5 试样破坏时侧向应变(%)Tab.5 Lateral strain during specimen failure

上述分析表明，侧向应变受干密度、围压共同影响。为了进一步探究干密度、围压与侧向应变三者的关系，依据试验结果整理出同一围压下，破坏时侧向应变与干密度的关系，如图7中试验点所示。

图6 不同干密度土体εv-εa曲线对比图Fig.6 Comparison of εv-εa curves of soils with different dry densities

图7 不同干密度土体侧向应变对比图Fig.7 Comparison of lateral deformation of soil with different dry densities

由图7可知，破坏时侧向应变与试样密度具有良好的线性相关性，因此用直线进行拟合：

εr=kρd+b

(2)

式中，εr为侧向应变(%)，ρd为试样干密度，k、b为拟合参数。将不同围压对应的k、b以及R2值(相关系数)列于表6中，R2均大于0.94，表明拟合良好。依据式(2)可估算在侧向卸荷条件下土体破坏时的侧向应变。

表6 不同围压对应的拟合参数值Tab.6 Fitting parameter values corresponding to different confining pressures

由表6可以看出，k、b的大小与围压相关，分别将它们与围压的关系在图8和图9中点绘出来。进一步研究发现，k、b的值与围压的关系可采用式(3)、(4)进行拟合：

k=C1lnσ3+D1

(3)

b=C2lnσ3+D2

(4)

式(3)、(4)中，σ3为固结围压(单位为kPa)，C1、D1、C2、D2为拟合参数。对于k值，C1、D1值分别为-1.62和10.20，R2可达0.987，对于b值，C2、D2分别为1.82和-4.44，R2可达0.961，拟合均较为良好。

图8 k值与围压关系试验点与拟合曲线比较Fig.8 Relationship between k value and confining pressure

图9 b值与围压关系试验点与拟合曲线比较Fig.9 Relationship between b value and confining pressure

依据式(2)—(4)，可以初步估计基坑等工程开挖后支挡结构的极限位移。假定支挡结构后土体破坏时主动破坏区范围如图10所示，滑动面与水平面夹角为(45°+φ/2)。从而，可以计算任意深度处的滑动区水平范围，如图10中的L。根据该埋深处土体的干密度及小主应力，就可用式(2)计算出破坏应变(极限应变，εr)，从而，该处的极限位移为uf=εrL，如果考虑一定的安全储备，该值就可以作为基坑变形监测的预警值。

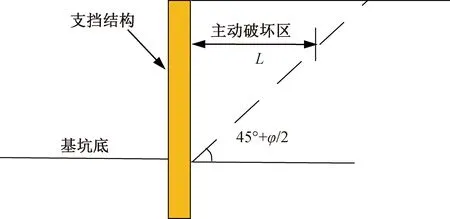
图10 支挡结构后土体主动破坏区范围Fig.10 Range of active failure zone of soil after retaining structure

3 结论

1)不同干密度粉质粘土试样在K0固结侧向卸荷路径下，均表现出明显的剪胀性，此性质与常规三轴压缩路径下相似；且随干密度的增加，土体的剪胀性増强，强度指标也逐渐增大。

2)依据试验结果，提出了一个土体因干密度变化引起内摩擦角变化的经验公式，利用该公式可以估计土体摩擦角随深度(密度)的变化，使得相关计算或设计更精细。

3)土体破坏时的侧向应变随着密度的增加而增加，但随着围压的增大，密度的影响逐渐减小。提出了一个侧向卸荷条件下土体破坏时侧向应变公式，并建议了据此公式估计基坑支挡结构的极限位移方法。