基于信赖域-遗传算法的雷电冲击试验波形参数估算
李忠诚,刘馨然,张穆昕
(国网辽宁省电力有限公司计量中心,沈阳 110000)
0 引言
冲击耐压试验作为高电压测试的一项主要内容[1],对于检验高压电器设备的绝缘特性发挥重要作用。准确的试验参数是确保设备安全可靠运行,预防绝缘损毁的重要保障。IEC 60060-1∶2010[2]标准对雷电冲击电压试验所用的测量技术及相关参数作出了明确。根据标准规定,雷电冲击全波电压波形可以通过双指数函数近似模拟,波形主要特征参数有3个:峰值、波前时间和半峰值时间。
对于模拟或数字记录的平滑雷电冲击电压波形,很容易计算得到特征参数,但实际上由于高压测试电路回路电感或测试设备杂散电容的存在,导致雷电冲击电压波形存在过冲或波前、波尾振荡现象,使得估算波形参数变得较为困难。针对这个问题,IEC 600660-1等标准[2-3]经过不断的修订,推荐引入试验电压函数k(f),对雷电冲击电压波形中的振荡部分进行滤波处理,将滤波后的剩余曲线与拟合基本曲线相加得到最终试验电压曲线,从而计算波形特征参数。IEC第三版本的标准有效避免了旧版本关于平均曲线的不精确处理,但在确定起始点、拟合平均曲线、构造滤波器等过程中仍然存在一些难点[4-6]。
为解决上述问题,国内外学者进行了大量研究,较为常见的方法是利用线性和非线性回归模型提取雷电冲击电压波形平均曲线[7-8]。遗传算法(GA)[9]、人工神经网络算法(ANN)[10]、粒子群优化算法(PSO)[11]也被用于曲线拟合。也有学者提出采用零相位滤波[12]等数字滤波技术、小波多分辨率分析[13]等手段消除波形过冲或振荡。需要指出的是,当前研究方法或多或少存在一些缺陷,例如,初始参数的选择会影响解的收敛性,导致曲线拟合技术不能提供精确参数估计,数字滤波技术可能导致波前时间的减少,基于小波分析的技术不能同时在时间和频率上都具有很高的精度。
本研究提出一种基于信赖域算法的雷电冲击波形平均曲线拟合方法,采用双指数函数构造波形平均曲线,引入遗传算法解决信赖域算法局部信赖域半径减小,迭代点难以求解的缺点,利用信赖域-遗传算法分别对雷电冲击波形存在过冲、波前振荡、波峰振荡、波尾振荡情况下拟合效果进行验证。
1 雷电冲击波形
根据相关规范[2],雷电冲击全波电压波形可使用双指数函数描述,具体形式如下:
V(t)=A(e-α(t-td)-e-β(t-td))
(1)
式中,A为冲击电压峰值;α和β是决定波形上升和下降的衰减常数;td为波形起始时间。对于标准雷电冲击电压波形,波前时间T1为1.2 μs,半峰值时间T2为50 μs。
根据参数定义,T1和T2计算过程如下[14]:
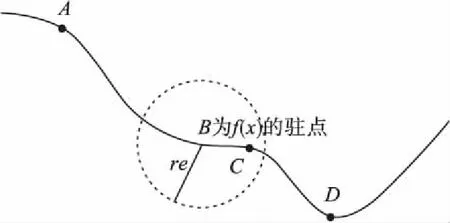
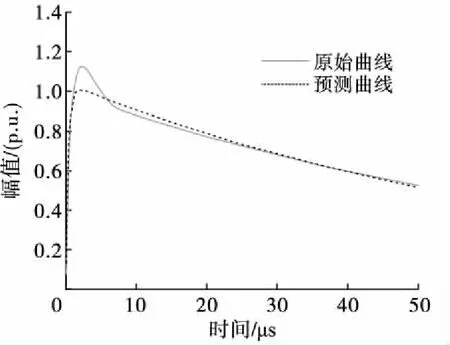
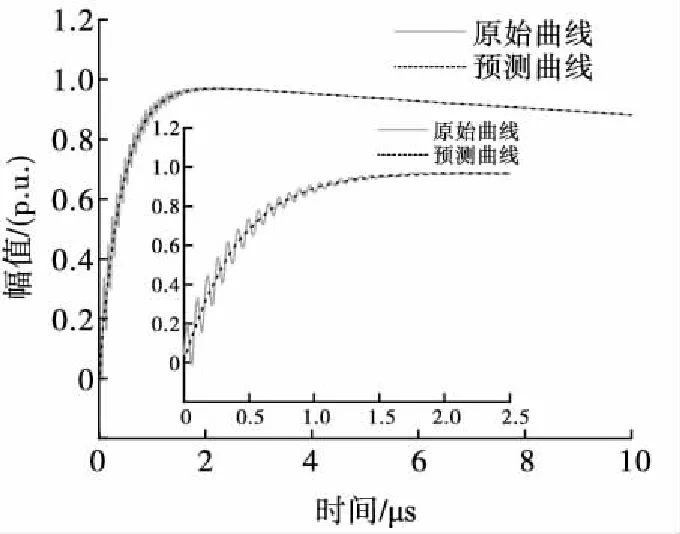
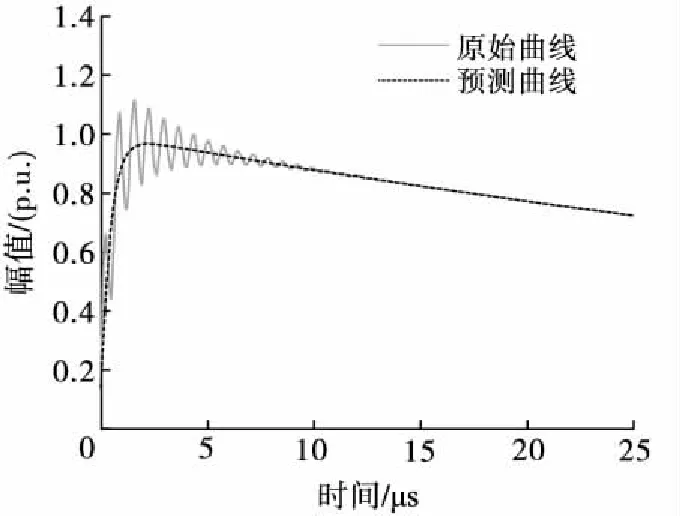
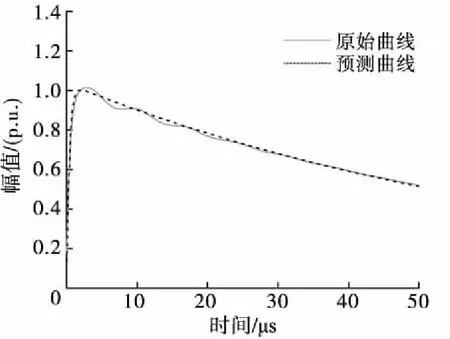
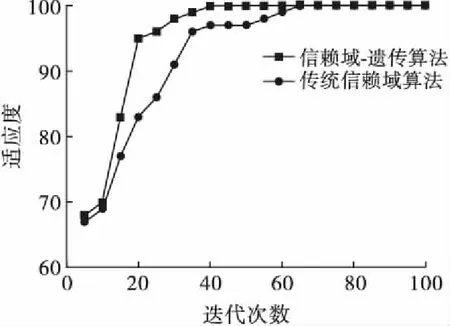
T1=1.67(t90-t30),0.84 μs (2) T2=(t50-td),40 μs (3) 式中,t30、t50、t90分别为到达试压电压峰值Vp的30%、50%、90%对应的瞬时时间。 波形起始时间可以通过下式计算: (4) t30、t50、t90可以通过牛顿迭代法求解下式方程而得[14]: (e-αt30-e-βt30)=0.3Vp/A (5) 雷电冲击全波电压波形参数(A、α、β)的确定可以看作一个优化问题[15],优化目的是尽可能降低预测波形和实测波形之间的误差。目标函数的选取至关重要,雷电冲击全波电压波形预测问题的目标函数考虑均方误差,具体数学表达形式如下: (6) J(A,α,β)=min(MSE) (7) (8) 式中,MSE为均方误差,vm为实际电压值,ve为预测电压值,N是测量数据样本总数。 寻找波形实测值和预测值之间的最小误差是一个最小二乘问题,通过求解目标函数的最优解(局部最小值),使得目标函数的值最小,从而能够优化的波形函数使之更加接近与真实的冲击波形。 信赖域算法是求解有界约束非线性极小化问题的一种简捷有效的手段,其基本思路是给定点初始迭代点x(k),确定一定的变化范围,取以x(k)为中心的闭球区域,称为信赖域,在此域内优化目标函数f(x)的二阶泰勒展开式,求取最优点,确定“候选位移”,若候选位移使得目标函数有充分下降量,则接受该候选位移作为新的位移,从而确定新的迭代点x(k+1);如果二阶泰勒展开式与目标函数的近似度不够理想,则缩小信赖域半径,重新定义x(k+1)为中心的信赖域,并在此域内优化新的二阶泰勒展开式,直到满足迭代终止条件。 信赖域算法的具体计算步骤如下。 1)给定初始迭代点x(1),信赖域半径r1,参数0<μ<η<1及误差限ε,置k=1,一般取μ=0.25,η=0.7。 2)对于某次迭代k,计算f(x(k)),∇f(x(k)),若‖∇f(x(k))‖<ε,停止计算,得解x(k),否则计算∇2f(x(k))。 4)若ρk≤μ,令x(k+1)=x(k),否则令x(k+1)=x(k)+d(k)。 5)修改rk,若ρk≤μ,令rk+1=0.5rk,如果μ<ρk<η,令rk+1=rk,如果ρk≥η,令rk+1=2rk。 6)k=k+1,重复步骤2)。 上述信赖域算法计算过程可以发现,新的信赖域的大小依赖于初始点的选取,迭代点变化速度受到信赖域半径的约束,导致全局最优解不易求取[16]。为此可以引入遗传算法,扩大的信赖域半径,在该信赖域内,求解一个比当前迭代点更优的点。图1给出了具体迭代点变化过程示意图[17]。 图1 信赖域-遗传算法迭代点变化示意图Fig.1 Changes of the iteration point in the trust region method combined with genetic algorithm 见图1,迭代点A点迭代到B点附近时,信赖域半径逐渐减小,难以找到一个有满意下降值的迭代点,影响了算法收敛速度。扩大在B点的信赖域半径{x‖x-xB‖≤re,x∈Rn},通过遗传算法求取更优点C,随后在新迭代点C点重复信赖域算法,直至找到最优点D点为止。 信赖域-遗传算法具体步骤如下[18-19]。 1)给定初始迭代点x(1),最小信赖域半径rmin,设置参数ε1>0,ε2>0,ε3>0,0<β1<1<β2,0<β3<β4<1,M1>1,令信赖域半径r1=max{‖∇f(x(1))‖,rmin}。 2)对于某次迭代k,计算f(x(k)),∇f(x(k)),若‖∇f(x(k))‖<ε1,终止计算,得解x(k),否则求解二次模型的最优解d(k)。 3)计算增益比例ρk,若ρk≤0,令x(k+1)=x(k),否则令x(k+1)=x(k)+d(k)。 4)选取rk+1,使其满足: 7)k=k+1,重复步骤(2)。 通过相关数学公式分别模拟生成伴有过冲、波前振荡、波尾振荡的雷电冲击波形原始数据,采用信赖域-遗传算法拟合波形平均曲线。 采用式(9)[20]生成伴有过冲现象的雷电冲击波形原始数据。 y(tk)=A(e-αkΔt-e-βkΔt)+Be-γkΔt(1-coswkΔt) (9) 式中,相关参数分别为:A=1,B=0.84,α=1.3×104,β=2.34×106,γ=6×105,w=5×15。 图2给出了伴有过冲现象的雷电冲击波形原始曲线和预测曲线。 图2 伴有过冲雷电冲击波形原始曲线与预测曲线Fig.2 Measured and estimated waveform of the lightning pulse with overshoot 图2可以看出,信赖域-遗传算法能够较好的拟合出符合原始数据曲线走势的雷电冲击波形平均曲线,拟合得到的双指数波形曲线参数为A=1.024,α=1.358×104,β=2.389×106,接近于原始冲击波形参数。 采用式(10)[20]生成伴有波前振荡和波峰振荡现象的雷电冲击波形原始数据。 y(tk)=A(e-αkΔt-e-βkΔt)+Ce-δkΔtsinwkΔt (10) 式中,波前振荡相关参数分别为:A=1,C=0.2,α=1.3×104,β=2.34×106,δ=2×106,w=8×107;波峰振荡相关参数分别为:A=1,C=0.3,α=1.3×104,β=2.34×106,δ=4×106,w=9×106。 生成伴有波尾振荡现象的雷电冲击波形的公式形式和式(9)类似,相关参数分别为:A=1,B=0.016 8,α=1.3×104,β=2.34×106,γ=1 000,w=5.1×105。 图3~图5分别给出了伴有波前、波峰、波尾振荡现象的雷电冲击波形原始曲线和预测曲线。 图3 伴有波前振荡雷电冲击波形原始曲线与预测曲线Fig.3 Measured and estimated waveform of the lightning pulse with oscillations on the front 图4 伴有波峰振荡雷电冲击波形原始曲线与预测曲线Fig.4 Measured and estimated waveform of the lightning pulse with oscillations on the wave head 图5 伴有波尾振荡雷电冲击波形原始曲线与预测曲线Fig.5 Measured and estimated waveform of the lightning pulse with oscillations on the tail 由图3~图5可以看出,信赖域-遗传算法能够根据振荡冲击曲线拟合出较为平滑的双指数函数波形,根据波前振荡曲线拟合得到的双指数波形曲线参数为A=1.008,α=1.287×104,β=2.317×106,波峰振荡曲线拟合得到的双指数波形曲线参数为A=1.011,α=1.273×104,β=2.308×106,波尾振荡曲线拟合得到的双指数波形曲线参数为A=1.014,α=1.264×104,β=2.294×106,3种情况拟合参数均较为接近原始冲击波形参数。从拟合效果来讲,波前振荡曲线拟合效果最佳,波峰振荡曲线拟合效果次之。 图6给出了信赖域-遗传算法和信赖域算法处理伴有波前振荡现象的雷电冲击波形收敛速度对比。 图6 两种算法收敛速度对比Fig.6 The convergence of the fitness values for two algorithms 图6可以看出,信赖域-遗传算法经过约40次迭代计算后能够满足精度要求,而传统信赖域算法需要经过超过60次迭代,信赖域-遗传算法的计算收敛速度要明显快于传统遗传算法。 本研究提出一种基于信赖域-遗传算法的雷电冲击波形平均曲线拟合方法,构造双指数函数形式的波形平均曲线,分别对雷电冲击波形存在过冲、波前振荡、波峰振荡、波尾振荡情况进行拟合验证,分析结果表明该算法能够较好拟合雷电冲击波形平均曲线波形,拟合得到的波形基本参数与原始波形参数较为一致。2 波形参数估计
2.1 目标函数
2.2 信赖域算法
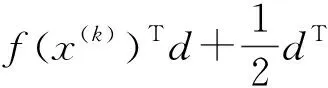
2.3 信赖域-遗传算法
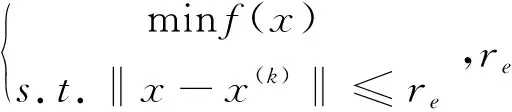
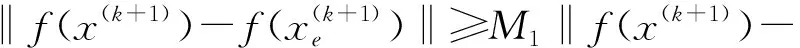
3 仿真结果分析
3.1 雷电冲击波形伴有过冲现象
3.2 雷电冲击波形伴有振荡现象
3.3 迭代速度
4 结论

