不同电压等级直线塔线路覆冰拉力值预警模型及核密度概率估计研究

吴建蓉， 姜 苏， 黄 欢， 彭 赤， 杜 昊

(1.贵州电网有限责任公司电力科学研究院，贵阳 550000；2.中国电建集团贵州电力设计研究院有限公司，贵阳 550000；3.贵州电网有限责任公司，贵阳 550000)

0 引 言

近年来，随着全球气候变化趋势日益复杂，导致不同地区局部小气候灾害性事件逐渐增多，尤其我国西南地区，每年因线路覆冰事件对电力部门造成较大的直接或间接损失[1-2]。同时，线路覆冰形成机理较为复杂，很难采用一种或者多种模型反映不同区域线路覆冰情况。同时，当前针对输电线路覆冰预测的研究，主要利用气象站预报数据，并结合导线覆冰物理模型进行预测[3-5]。但在实际应用中，输电线路往往距离气象站点较远，对线路通道临近区域覆冰因子预测精度也较差，难以运用到实际工作中。而目前电力部门对于线路覆冰预警仍属于被动防御，即通过安装在线监测终端，对线路拉力值进行测量，然后反算出覆冰厚度[6-7]，这种方式通过拉力值实时变化，反映出线路覆冰情况，在实际运用中能够较好的了解线路覆冰情况，当线路覆冰比值达到一定阈值时，电力部门能够及时启动线路融冰计划。但通过拉力值反算出冰厚，计算模型所涉及到参数较多，比如水平档距、高差、垂直档距、等效长度、导线型号、气象条件等，计算准确度对模型输入参数质量具有较大依赖性，且在冬季气温较低条件下，往往会造成气温、相对湿度传感器灵敏度下降，导致气象条件测量不准确，以上问题将直接带来计算结果存在一定的偏差。因此，直接利用线路无覆冰时拉力测量值，找出冰期满足线路融冰条件拉力阈值，并总结其适用的规律，实现通过拉力值变化判断是否需要启动融冰具有重要意义。

针对线路覆冰技术方面的研究，Jones[8]在1998年首先提出了雨凇计算模型，但目前大多数线路覆冰不仅仅是单一的雨凇，还有雾凇、雪凇、混合凇等情况。谭伟等[9]在Jones模型的基础上，提出了雾凇模型，从而相结合得出混合淞模型，并运用至南方四省冰区分布图研究工作中。朱晔等[10]通过在线监测技术，对线路覆冰4个关键气象因子观测，并建立了覆冰趋势预警模型。张乐等[11]从力学角度出发，建立线路覆冰综合荷载模型，并利用导线疲劳度因子，对线路覆冰厚度计算结果修正。郝艳捧等[12]采用小波分析方法，对线路覆冰进行图像识别，并与实际覆冰监测数据比对，识别误差小于2.5 mm。虽然还有很多学者采用不同的方法对线路覆冰方面进行了研究，总结起来主要有3个方面：第一个方面，利用覆冰关键气象因子数据、覆冰数据，并建立统计关系表达式，但该方法还是存在一定的弊端，即对气象传感器抗冻、抗潮湿性能要求较高；第二个方面，采用图像识别技术对覆冰厚度监测，但在山地较为复杂的区域冬季往往雾气较大，且视频监控镜头容易结冰，使得摄像头很难较为准确、清晰的拍摄到线路覆冰图像；第三个方面，利用在线监测终端拉力测量值，再反算出冰厚，这种方式对模型计算参数准确性要求较高。

针对上述分析，本研究建立覆冰比值达到融冰预警、启动融冰条件下拉力值计算模型，并对计算出的不同电压等级线路拉力融冰预警、启动融冰阈值分析，研究其统计学规律，旨在找出拉力值预警适用范围，从而实现线路覆冰实时预警，为线路融冰计划提供科学指导，保证主干电网安全稳定，对保证地级市、县城冰期稳定供电具有重要意义。

1 拉力值计算模型理论

根据《110 kV-750 kV架空输电线路设计规范》[13]中导线状态方程，建立线路拉力值计算模型(究主要研究直线塔线路)，图1为拉力值覆冰预警计算方法流程：首先设定冰期输电线路覆冰比值预警阈值(根据贵州省电网公司融冰启动业务需求确定，当覆冰比值达到0.3时，为融冰预警；当覆冰比值达到0.5时，启动融冰)，计算出该阈值情况下输电线路等值覆冰厚度：

(1)

公式(1)中：Δd为设定冰期输电线路覆冰比值预警阈值(本研究Δd分别取值0.3、0.5)。

因此，覆冰时导线单位长度风荷载计算表达式为

gf=0.000 625v2·(D+2d)·u·Vfx

(2)

公式(2)中：v为工况设计风速，D为导线直径，u为导线受风体型系数，Vfx为线路风压系数。

直线塔覆冰在线监测终端拉力传感器安装于垂直向下的绝缘子串上，因此覆冰时导线单位长度综合荷载计算表达式为

(3)

公式(3)中：mg为导线单位长度重量，gb为导线单位长度覆冰重量，C为覆冰时绝缘子串总重量。

根据导线状态方程表达式[7]：

(4)

公式(4)中：gi为覆冰时单位长度导线应力，E为导线弹性模量，a为导线温度膨胀系数，ti为覆冰时环境温度，导线设计环境工况温度。

根据公式(4)计算出的不同覆冰条件下导线应力gi，建立导线垂直档距变化过程表达式：

Li=L+(gi/gfb)·(Lc-L)(gλ/Fλ)

(5)

公式(5)中：L为水平档距，Lc为导线设计时单位长度比载，gλ为导线设计时导线水平应力。

因此，根据上述计算过程，可以建立覆冰时导线垂直荷载，即拉力值表达式为

Lg=nLigfb

(6)

公式(6)中：n为导线分裂数。

图1 拉力值覆冰预警计算方法流程Fig.1 Calculation process of tension value ice coating early warning

2 研究分析

2.1 拉力值计算及融冰条件分析

本研究利用上述拉力值覆冰预警计算过程，分别计算出安装有覆冰在线监测终端线路覆冰比值Δd=0.3、0.5两种情况下拉力预警临界值，然后对拉力比值进行定义：

Ci=LgΔd/LT

(7)

公式(7)中：LT为无覆冰时拉力初始值，LgΔd为覆冰比值Δd分别取值0.3、0.5条件下拉力值，其中覆冰比值Δd=Lg/LS，LS为线路设计冰厚。

其中对于无覆冰条件下拉力初始值取值原则，本研究统计每个终端7月份内拉力平均值表示各个终端的拉力初始值。首先本研究按照覆冰比值0.3、0.5两种条件定义线路覆冰拉力比值，即在线路覆冰比值分为0.3、0.5时，所对应的拉力值除以无覆冰时拉力代表0.3、0.5比值；其次以安装有覆冰在线监测终端200条110 kV线路为例，图2为110 kV线路覆冰拉力比值分布情况，可以看出覆冰比值0.3、0.5条件下计算出拉力值比分别分布于1.0～4.65、1.08～6.11之间，对于同一个终端(样本)计算出的覆冰比值0.5条件计算出的拉力比值要大于0.3条件。同样的方法计算出115条220 kV、36条500 kV线路0.3拉力比值分别分布于1.05～1.94、1.06～1.87之间， 0.5拉力比值分别分布于1.11～2.99、1.13～2.80之间。上述分析可以看出，220 kV、500 kV线路拉力值比较为集中，而110 kV线路较为分散，主要是因为220 kV、500 kV线路覆冰在线监测终端所在杆塔档距相差较小，因此线路覆冰时拉力值分布较为均匀，而110 kV线路档距相差较大，从而线路覆冰拉力值具有较大的差异性。

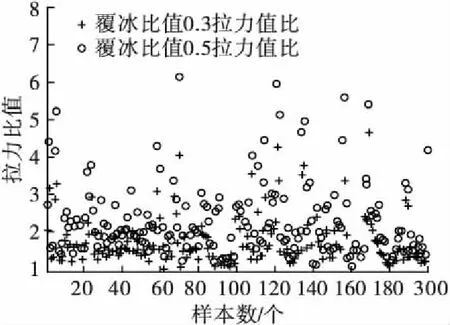
图2 110 kV线路覆冰拉力比值分布图Fig.2 Distribution diagram of ice covering tension ratio of 110 kV line

针对上述分析，虽然得到不同线路覆冰比值0.3、0.5融冰预警条件下拉力比值，但并不能找出一个固定值，通用于各条线路拉力预警，且通过图2发现，拉力比值在某个较小的区间分布较为集中，少数样本拉力比值较分散，造成这种原因，主要是由于少部分在线监测终端拉力测量值本身存在一定的偏差。因此，为克服少部分线路拉力测量值不准确的缺陷，减少对研究结论准确性所造成的影响，本研究采用核密度估计方法(ksdensity)[14]，以110 kV线路为例对200条样本线路(安装有在线监测终端)拉力比值进行概率密度分布计算，核密度估计方法不需要事先预知样本的分布规律，对样本的初始分布没有任何假定限制，是直接从样本出发研究其分布特征。核密度估计方法核心表达式为[15]

(8)

公式(8)中：n为样本数，Δl为拉力比值窗口间隔(本研究取值0.01)，K()为核函数，xi为独立分布的样本点。

则每个拉力比值分布概率计算公式为

pi=ηi×Δl×100%

(9)

图3为计算出的不同拉力比值条件下概率密度分布，可以看出0.3、0.5两种拉力比值均在某个区间较为集中，分别在1.3～1.8、1.4～2.5之间较为集中，其余区间分散较为薄弱，同时根据公式(8)计算出这两个区间上的累积概率分别为：90.02%、91.16%，这说明了90.02%的样本融冰预警条件能够用1.3～1.8拉力比值分布范围表示；同理91.16%的样本启动融冰条件能够用1.4～2.5拉力比值分布范围表示。

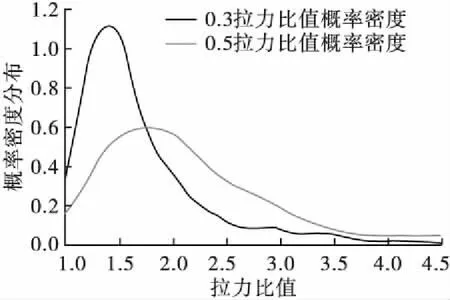
图3 110 kV线路不同拉力比值条件下概率密度分布图Fig.3 Probability density distribution under different tension ratio

最后计算出两个集中区间的均值分别为：1.55、1.96。因此，对于110 kV线路，当冰期拉力值为初始值的1.55倍时，为融冰预警条件阈值(即覆冰比值0.3条件)，当冰期拉力值为初始值的1.96倍时，为启动融冰条件阈值(即覆冰比值0.5条件)。

本研究运用同样的方法，分别对220 kV、500 kV线路不同拉力比值概率密度分布进行计算，结果见统计表1。可以看出，220 kV、500 kV线路融冰预警、启动融冰拉力值变化条件较为一致，即220 kV线路拉力比值分别为1.26、1.41，500 kV线路为1.21、1.43，说明了在冰期拉力值为初始值的1.26倍时，220 kV线路需要进行融冰预警，而达到1.41倍时，开始启动融冰。对于500 kV线路同理，在冰期拉力值为初始值的1.21倍时，需要进行融冰预警，而达到1.43倍时，开始启动融冰。

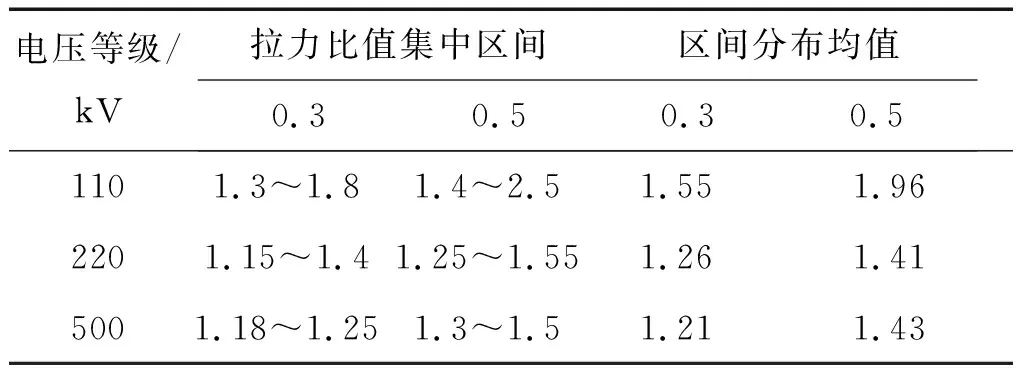
表1 不同电压等级线路拉力比值概率密度分布统计Table 1 Probability density distribution statistics of line tension ratio of different voltage levels

2.2 案例对比分析

为验证上述所得出的线路融冰预警、启动融冰条件拉力阈值，结合2020年冰期线路实际覆冰情况进行比对。图4为贵州省2020年春节期间一次寒潮过程应急响应期间线路最大覆冰分布情况，可以看出在这次寒潮过程中共计113条线路出现覆冰事件，其中1条线路覆冰大于10 mm，14条线路覆冰在5～10 mm之间，其余线路覆冰相对较轻。表2为覆冰5 mm及其以上线路人工观冰统计结果。

图4 贵州省2020年春节应急响应期间线路覆冰分布情况Fig.4 Distribution of line icing during Spring Festival emergency response in 2020 of Guizhou Province

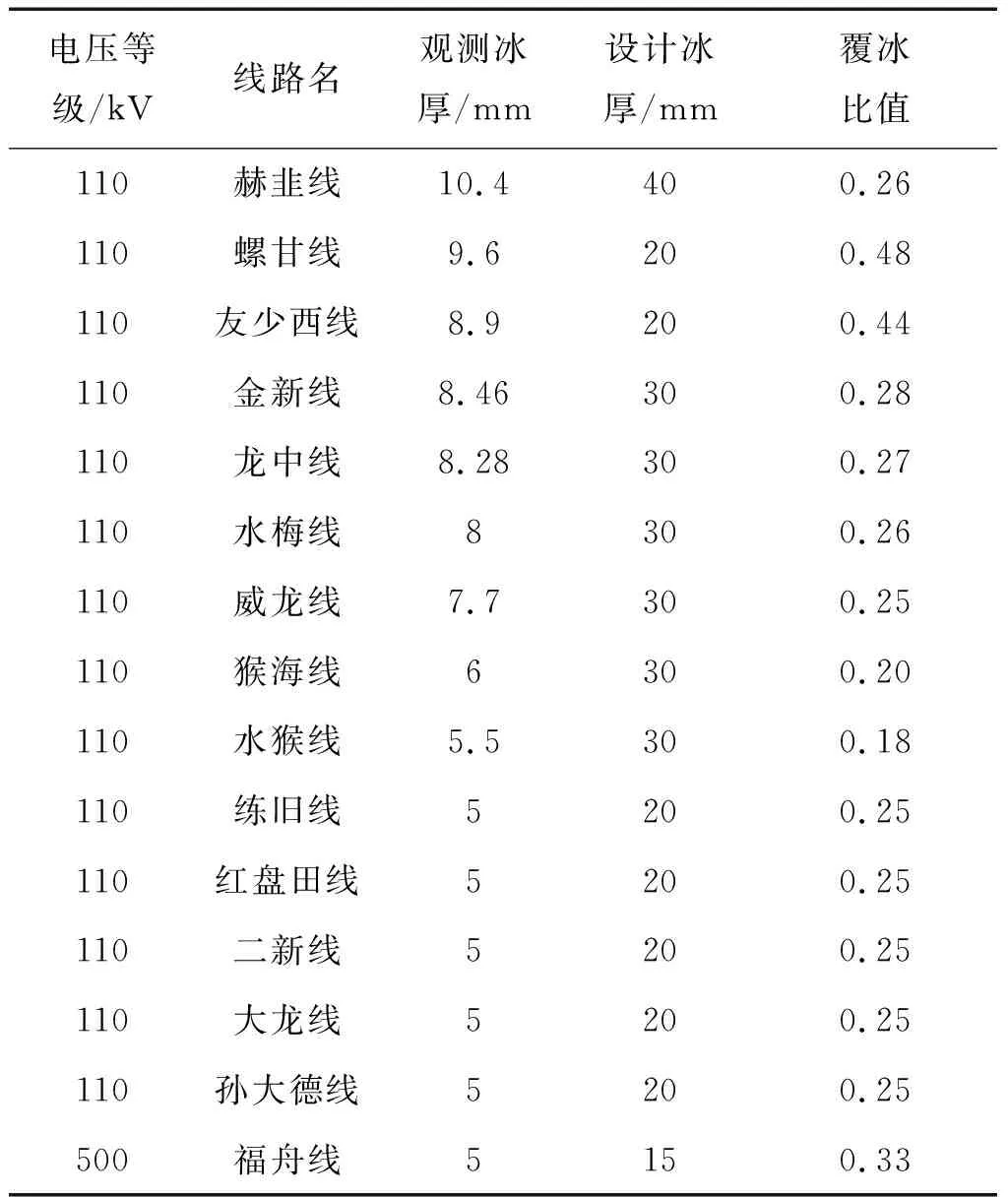
表2 人工观冰统计结果Tabele 2 Statistical results of artificial ice observation

从表2中可以看出，螺甘线、友少西线、福舟线这3条线路覆冰比值分别为0.48、0.44、0.33，达到贵州省电网公司线路融冰预警覆冰比值0.3的阈值要求，且这3条线路均为直线塔，因此本研究利用这3条线路覆冰监测系统拉力值观测数据对表1中的结论进行验证。其中3条线路覆冰在线监测终端分别安装于7号、29号、154号塔位，以友少西线为例，图5为该线路拉力值变化趋势及人工观冰结果，可以看出人工观冰厚度整体变化趋势与拉力值较为一致。表3为3条线路拉力值变化及同期对应人工观测覆冰厚度统计情况。

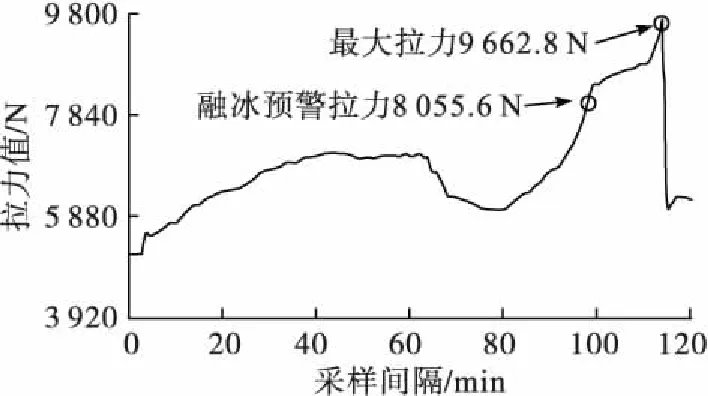
图5 友少西线拉力值变化趋势及人工观冰结果Fig.5 Variation trend of tensile force and artificial ice observation results

通过表3实际观测资料可以看出，对于螺甘线7号塔位线路无冰拉力值为3 224.2 N，寒潮期间所观测覆冰比值为0.48处于0.3～0.5之间，对应同期最大拉力值为6 203.4 N，拉力比值为1.92，当覆冰比值达到0.3时，观测到拉力值为4 860.8 N，拉力比值为1.51。对应表1可以看出，对应110 kV线路覆冰比值0.3时，拉力比值临界值为1.55，即覆冰拉力值为无冰拉力值的1.55倍，发布融冰预警，该1.55临界值与实际观测的1.51相对误差为2.58%。同理，对于友少西线覆冰比值0.3时，本研究计算出的拉力预警比值与实际观测的相对误差为0.81%；对于500 kV福舟线覆冰比值0.3时，拉力观测值为16375.8 N，拉力比值为1.19，对应表1拉力融冰预警值1.21相对误差为1.65%。

综上对本次寒潮过程覆冰较为严重的3条线路拉力观测值变化趋势分析，可以看出本研究计算出的拉力预警比值能够很好的运用至线路融冰预警实际业务中。

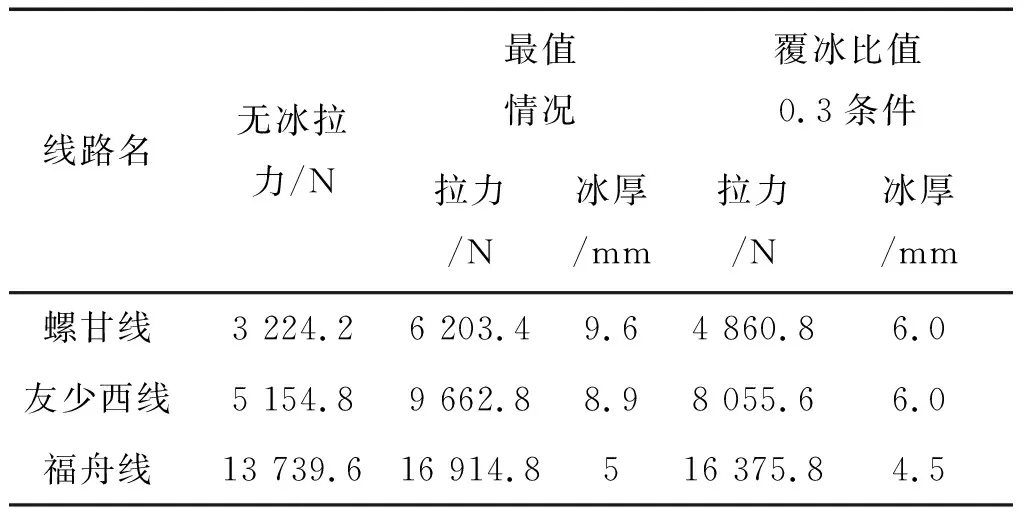
表3 拉力值变化及观冰统计结果Table 3 Statistical results of tensile force and ice observation

3 结论

结合线路设计规范，从力学角度出发，建立线路覆冰拉力受力计算模型，以200条110 kV线路、115条220 kV、36条500 kV线路为研究样本，分别按照覆冰比值0.3、0.5两种条件对拉力值进行计算，并采用核密度估计方法分析其统计学规律，主要有以下结论：不同电压等级线路拉力比值在某个较小的区间分布较为集中，少数样本拉力比值较分散；110 kV、220 kV、500 kV线路融冰预警拉力比值分别为1.55、1.26、1.21，启动融冰拉力比值分别为1.96、1.41、1.43；最后利用2020年寒潮过程3条线路实际覆冰观测资料对本研究所得结论进行了验证，指出本研究给出的拉力比值能够很好的运用至线路融冰预警实际业务中。