基于Heaviside投影和进退法的结构拓扑优化方法
吴振雨 罗城升 陈保家 王林军
(1.三峡大学 水电机械设备设计与维护湖北省重点实验室,湖北 宜昌 443002;2.三峡大学 机械与动力学院,湖北 宜昌 443002)
拓扑优化是在给定约束的情况下对结构进行设计,且要在保证结构性能不变的同时得到所需结构.随着Bendsøe等[1]提出均匀化方法,连续体的拓扑结构优化得到飞速的发展.Bendsøe等[2]提出固体各向同性材料惩罚(SIMP)法;Reitz等[3]提出材料属性有理近似(RAMP)法,为结构拓扑优化奠定了基础.Andreassen E等[4-6]编写了一种高效的拓扑结构优化代码.该代码包含了灵敏度过滤、密度过滤和Heaviside投影函数过滤3种过滤方法,以保证优化过程的稳定性以及避免棋盘格现象.随着拓扑优化的逐渐完善,很多学者在变密度法的基础上进行了拓展研究.高翔等[7]针对结构优化过程中的效率问题,提出一种针对Lagrange乘子的改进导重法过滤技术.陈垂福等[8]基于步长因子进行改进导重法求解拓扑优化问题.高翔等[9]提出了一种改进的导重法求解拓扑优化问题及抑制灰度单元技术.任毅如等[10]针对自重载荷悬臂梁结构末端不收敛问题进行了研究.焦洪宇等[11]提出了一种基于导重法的结构类周期性布局优化方法.江旭东等[12]研究了导重法下的功率流响应问题.李启宏等[13]针对在不同规模网格下优化结构的性能问题,提出了一种改进的SIMP 优化方法.赵婉霖等[14]针对SIMP 法提出了一种多约束的连续体优化方法.以上学者的研究涉及到导重法、多约束问题、布局优化和抑制灰度单元等领域,但这些研究均未在考虑收敛性问题的基础上探讨提升优化效率的问题.因此,本文在基于收敛性问题的基础上对提升优化效率进行了研究.在Heaviside投影函数的基础上改进进退法替代二分法进行计算,提高计算效率的同时,提高了收敛性.
1 传统拓扑优化模型
连续体拓扑优化的目标是使得柔度最小[14],其优化模型为:

式中:X e为第e个单元的密度;C(X e)为结构柔度;K为整体刚度矩阵;U为位移向量;F为外部载荷;V(X e)为迭代过程中实体的体积;V0为初始设计域的总体积;f为材料的体积分数(最终剩余的材料体积占初始设计域总体积的百分比).设计变量的取值在0~1之间变化.
SIMP法的插值函数模型和柔度的灵敏度分别为:

RAMP法的插值函数模型和柔度灵敏度分别为:

式中:E e为第e个单元的弹性模量;X e为第e个单元的密度;E0和Emin分别为弹性模量的上限和下限;p为SIMP法中的惩罚因子;q为RAMP 法中的惩罚因子.
SIMP和RAMP的体积灵敏度均为:

由图1可知,在p=1,q=1时,SIMP 为一条线性直线,RAMP 为一条凹曲线.在相同单元密度下,SIMP的弹性模量大于RAMP;p=4,q=4时,SIMP和RAMP两条曲线相似,但在两条曲线交点之前,相同密度下SIMP 比RAMP 的弹性模量要小;在p=8,q=8 时,两条曲线交点之前,在相同的密度下SIMP比RAMP的弹性模量要小.

图1 SIMP和RAMP插值函数模型的对比
综上,SIMP在p=1 到p=4 之间曲线变化较大,但在p越大的时候惩罚力度大于RAMP.RAMP在q逐渐变大时曲线变化较小,整体稳定性比SIMP好,但惩罚力度略有不足.采用改进的进退法对这两种不同的计算弹性模量的方法进行目标函数的求解,更进一步说明改进进退法的适用性.
2 模型的改进
2.1 迭代方法的改进
二分法及进退法都是一维区间搜索法,且能有效地求解最小值问题,但二分法的求解效率低于进退法.本文在文献[9]的基础上对进退法进行改进.
(1)二分法

2.2 插值函数模型
由于变密度法所得优化结构中存在大量的灰度单元,导致结构边界不清晰,从而丧失了实际的工程应用意义.因此采用Heaviside投影函数对灰度单元进行抑制,减少结构中的灰度单元数量,以获得具有更加清晰边界的优化结构.
Sigmund等[6]基于Heaviside投影函数提出一种插值函数,插值函数和导数分别为:
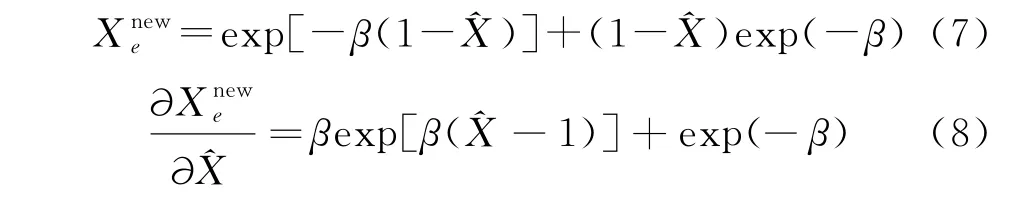
高翔等[7]在Sigmund等[6]的基础上进行了改进并提出一种新的插值函数,函数及导数分别为:

如图2所示,式(7)和式(9)两个函数图形基本相似,但式(9)相对于式(7)具有一定程度的提升.为了更全面地印证改进进退法的优点,采用这两个插值函数对改进的进退法和二分法进行对比.

图2 公式(7)和公式(9)的图形对比
3 算例验证
3.1 简支梁的拓扑优化
简支梁拓扑结构简图如图3所示,简支梁优化离散单元长为120,宽为60.集中载荷在简支梁下端正中间位置.
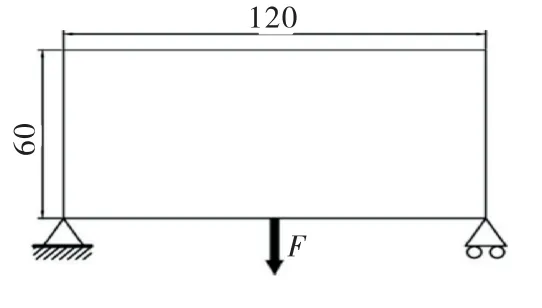
图3 二维简支梁简图
设置参数弹性模量上限E0=1,下限Emin=1×10-9,集中力大小F=1,体积比f=0.5,过滤半径rmin=2.5,SIMP和RAMP的惩罚因子p=3,q=3,β=1.将投影函数式(7)和式(9)分别应用于SIMP和RAMP方法中,分别采用二分法和改进的进退法两种优化算法进行计算.
由于式(7)中部分方法无法收敛,最终结构不可用,故选取式(9)中的结构进行对比,如图4所示,不论是二分法还是改进的进退法,均能得到较好的拓扑优化简图.

图4 简支梁的拓扑结构简图
由图5和图6可知,式(7)和式(9)在二分法和改进的进退法两种迭代模式下,柔度曲线的变化趋势相同但不完全重合.

图5 二分法中各公式的柔度迭代过程

图6 改进的进退法中各公式的柔度迭代过程
由表1可知,改进的进退法所需的迭代数小于二分法.式(7)采用SIMP方法时.改进的进退法迭代数相对于二分法减少了40.9%;式(9)采用SIMP方法时,改进的进退法迭代数相对于二分法减少了37.1%;式(9)采用RAMP方法时,改进的进退法迭代数相对于二分法减少了43.8%.

表1 二分法和改进的进退法对简支梁计算后的结果
3.2 悬臂梁的拓扑优化
悬臂梁拓扑结构简图如图7所示,悬臂梁左端固定,悬臂梁的长为120,宽为50,右下角承受集中载荷F.设置参数弹性模量上限E0=1,下限Emin=1×10-9,集中力大小F=1,体积比f=0.5,过滤半径rmin=2.5,SIMP和RAMP的惩罚因子p=3,q=3,β=1.

图7 二维悬臂梁简图
由于式(7)中SIMP法无法收敛,故选取式(9)的最终拓扑结构简图进行对比,如图8所示,二分法和改进的进退法均能得到较好的拓扑优化简图.

图8 悬臂梁的拓扑结构简图
由图9和图10可知,式(7)和式(9)在二分法和改进的进退法两种迭代模式下,柔度曲线的变化趋势相同但不完全重合.

图9 二分法中各公式的柔度迭代过程

图10 改进的进退法中各公式的柔度迭代过程
由表2可知,改进的进退法所需的迭代数小于二分法.式(7)采用RAMP 方法时,改进的进退法迭代数相对于二分法减小了42.9%;式(9)采用RAMP方法时,改进的进退法迭代数相对于二分法减少了42.3%;式(9)采用SIMP方法时,二分法出现无法收敛的问题,而改进的进退法可以收敛并能得到较好的拓扑优化结构,且所需的时间也较小.从而可知改进的进退法不仅迭代效率高于二分法,而且收敛效果也优于二分法.

表2 二分法和改进的进退法对悬臂梁计算的结果
4 结论
本文改进了一种新的进退法,并将其应用于两个不同的插值函数进行计算.同时采用了SIMP 法和RAMP 法两种弹性模量插值方法,并增加了本文方法与二分法的对比.两个算例的计算结果表明:改进后的进退法相对于二分法,计算所需的步数以及迭代数明显减小,能够在保证结构柔度的情况下较大地提升迭代的速度.因此,与二分法相比,改进的进退法效率更高,收敛效果更好.
本文仅对普通二维算例进行了研究,以后可将本文方法应用于三维以及其他工程方面的算例.

