基于数据挖掘的航道开挖过程中邻近桥墩变形预测
汪 彦 张 薇 余 杰 顾祯雪 宋德威 孙 阳,3,4
(1.杭州京杭运河二通道建设投资有限公司,杭州 330104;2.河海大学 港口海岸与近海工程学院,南京 210098;3.河海大学 淮安研究院,江苏 淮安 223001;4.河海大学 海洋与近海工程研究院,江苏 南通 226000)
结构物的变形量能够真实反映周围土体受到扰动后的响应结果,地下工程由于隐蔽性强,土体和结构物的变形不易观察,各结构物之间的变形、受力特性的关联性难以摸清.随着可编程计算机技术的进一步发展,人工智能数据挖掘方法逐渐被运用到现场测试数据分析领域,用层次化的概念体系来整合理解规律.
Agrawal等[1]最早提出关联法则,Agrawal等[2]提出了实现关联规则的Apriori算法,此后许多学者对关联规则的挖掘和算法的改进进行了研究[3-5],并从避免局部陷入鞍点、加快收敛速度、提高网络容错率、引入新的智能算法[6-8]等方面进行了优化.近年来国内外学者倾向于将数据挖掘应用于边坡变形预警、深基坑开挖稳定性分析、基坑对邻近构筑物的安全评估与风险控制等实际工程[9-18],对结构物的响应做出合理预测,并对发生的原因进行解释.
目前将数据挖掘应用于航道下穿高铁工程中的案例较少,常用的数据分析方法所依赖的假设缺乏严格的理论指导,仅是一种经验规则,缺乏客观性.本文结合京杭运河二通道(杭州段)下穿沪昆高铁工程,建立了桥墩变形量的一维响应预测模型和多维响应预测模型,验证数据挖掘技术在该实际工程中的可行性.达到降低施工风险、有效指导施工的目的,进而为类似工程中结构物的变形预测提供有效方法.
1 响应模型的建立原理
1.1 GM(1,1)模型
GM(1,1)在实际工程应用中比较广泛,具体的模型建立方法如下:
首先对原始数据X(0)进行累加,弱化其波动性和随机性,接着根据灰色理论,对累加后的数据X(1)建立关于时间t的白化形式一阶一元微分方程:

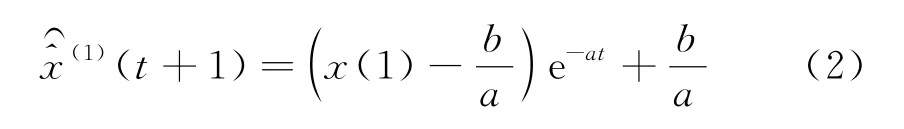
将其离散化得到白化响应式:

最后进行累减还原得到预测值:

1.2 GM(1,n)模型

将上述公式离散化,并构造矩阵形式的微分方程:

最后对式(7)经过累减还原即可对原始序列进行拟合和预测.
1.3 残差修正
假设灰色模型预估值与原始序列之间的残差序列如下:

对原始残差序列进行正化处理,并利用波形数据生成法将处理后的结果转化为单调递增序列,记为E2(k).

式中:ε1(k)=ε(k)+2|minε(k)|,ε2(k)=ε1(k)+d(k),k=1,2,…,n.

若一次残差修正后的模型精度仍不满足要求,可重复进行多次修正,直至预测模型的误差满足限定的要求.
2 桥墩变形预测
2.1 工程概况
京杭运河二通道(杭州段)新开挖航段,是京杭运河三级航道整治工程中投资最大的部分,也是建设的难点和重点,项目全长26.4 km,于航道里程K26+682处下穿沪昆高铁,如图1所示.

图1 下穿段受影响桥墩
受新建航道影响,为防止航道两侧邻近桥墩因土体开挖释放单侧约束而造成的基础与桥墩侧向偏移,保证客运专线的结构及运营安全,需对沪昆高铁海杭特大桥京杭运河桥段48+80+48 m 连续梁中墩232号桥墩和233号桥墩的位移量进行密切关注.
2.2 基于GM(1,1)模型的一维响应模型
2.2.1 模型可行性验证
选择232号桥墩墩顶竖向位移测量值作为原始数据,共提取22个值,选择前5个数据作为原始序列模拟桥墩的竖向位移发展情况,接着与测量结果对比,进行灰色模型预测可行性的验证.
设X(0)为桥墩墩顶竖向沉降的原始序列,则:X(0)={-0.723,-0.712,-0.679,-0.648,-0.645}.
对原始序列进行平滑性检验,令σ(0)(k)为X(0)在k点的级比:
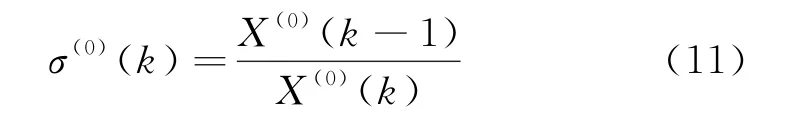
桥墩墩顶竖向沉降的级比序列为:σ(0)(k)={1.015,1.049,1.048,1.005}.σ(0)(k)属于区 间[1.005,1.049].令μ为测度,则有:μ[1.005,1.049]=|1.049-1.005|=0.044,此时μ<0.2,可以认为桥墩墩顶竖向沉降的原始序列X(0)是光滑序列.
2.2.2 模型计算与分析
桥墩墩顶竖向沉降的原始序列为X(0)={-0.723,-0.712,-0.679,-0.648,-0.645},计算出a=0.0349,b=-0.7440.代入式(3)和式(4)可得离散化的白化响应式为:



表1 基于5数值的计算结果与误差检验

续表1 基于5数值的计算结果与误差检验
经过初步分析,发现紧邻原始序列的预测值相对误差较小,精度较高.因此考虑减小预测值的个数,将精度较高的、临近原始序列的预测值加入原先的原始序列,剔除位于原始序列前端等数量的数值,组成新的二次序列作为原始序列,采用等维灰数递补模型进行桥墩墩顶竖向位移的预测,计算结果见表2.
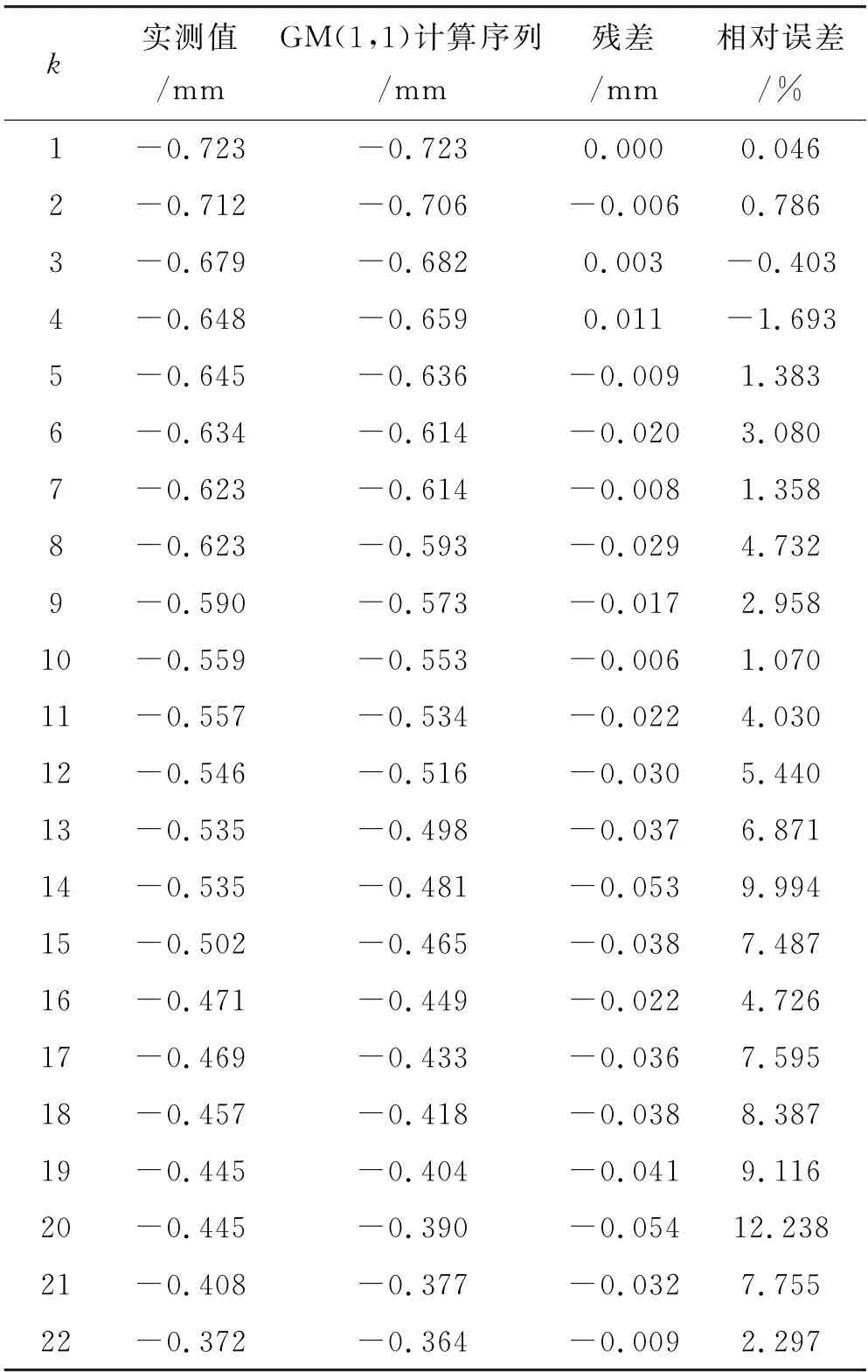
表2 基于等维灰数递补模型的5数值计算结果与误差检验
为了研究不同原始序列个数对灰色模型的预测精度的影响,再分别取前8个原始数据和前10个原始数据作为原始序列进行计算,不同模型的计算结果误差比较如图2~3所示,可以看出预测的相对误差在0.046%至2.5%之间.

图2 桥墩墩顶竖向位移预测结果比较

图3 桥墩墩顶竖向位移预测误差比较
对比可以发现灰色模型的预测精度随着原始数据的增加而增加,且高精度预测值集中在原始序列之后的几个值中,越往后误差越大.等维灰数递补模型在原始序列数目不变的情况下,能显著提高小样本灰色模型模拟的精度.
2.3 基于关联法则联合GM(1,n)模型的多维响应模型
2.3.1 关联法则挖掘相关因素
灰色系统目标变量为桥墩墩顶竖向位移,相关变量航道中心坑底竖向位移,内、中间和外围护桩桩顶的竖向位移和水平位移,内横撑轴力,外横撑轴力,近外围护桩的地表沉降以及桥墩墩顶竖向位移,分别用A、B、C、D、E、F、G、H、J、K和X表示.每组均有8个数据.假设该数据为8周内的数据,计算每周的变化率.为了消除不同类别对象变化速率的差异,便于分析和比较,使用最大值最小值区间划分的方法,通过式(14)将各监测项目的变化速率均局限在[0,1]区间内:

对各监测项目的速率大小进行分类,分类方式见表3.

表3 监测项目速率变化分类
当监测项目的变化速率为中等即以上时,假定该监测项目变化较为显著.列出关于时间的显著变化数据库事务列表,见表4.

表4 数据库的事务列表
假定强关联规则的最小支持度阈值min_Support=30%,最小置信度阈值min_Confidence=70%.逻辑蕴涵式A⇒B的含义为在数据库中,A的发生与B有关.经计算,与桥墩墩顶竖向位移X有关的频繁项集为{AX}、{BX}、{CX}以及{BCX},其中B⇒X、C⇒X以及BC⇒X的置信度均为75%,大于min_Confidence=70%,根据Apriori算法,上述关联法则为强关联法则,表示当桥墩墩顶竖向位移变化速率较大时,内围护桩和中间围护桩的桩顶竖向位移变化速率也较大,他们的关联度较为紧密.因此可以将内围护桩和中间围护桩的桩顶竖向位移作为GM(1,n)模型的相关序列代入计算.
2.3.2 GM(1,n)模型计算与分析
模型相关因子个数为2,取前5周的数据作为原始序列进行计算预测,即每个序列的长度为5.因此取桥墩墩顶竖向位移、内围护桩和中间围护桩的桩顶竖向位移作为变量建立GM(1,3)模型.

计算出a=-0.2680,b1=-14.6112,b2=25.4977,进而得出GM(1,n)模型下的桥墩墩顶竖向位移,计算结果见表5.

表5 基于GM(1,1)模型和GM(1,n)模型的桥墩墩顶竖向位移计算结果与误差检验
从表5可知,GM(1,1)模型的最大相对误差为16.756%,发生在预测值的终值.后验差比值c=0.211 4,小误差概率p=1,模型精度为Ⅰ级.GM(1,n)模型的最大相对误差为18.874%,发生在数值拟合阶段.后验差比值c=0.435 0,小误差概率p=0.875,模型精度为Ⅱ级.
总的来看,GM(1,1)模型的预估值和预测值与有限元计算结果的关联度更高,GM(1,n)模型的预测效果前期不如GM(1,1)模型精度高,但预测后期精度比GM(1,1)模型更高.
3 结语
本文结合京杭运河二通道(杭州段)新开挖航段下穿沪昆高铁工程,提供了一种基于数据挖掘的新建航道开挖及老旧航道扩建升级过程中邻近建筑物变形演化规律的预测方法.并通过基于GM(1,1)模型的一维响应预测模型,以及基于关联法则联合GM(1,n)模型的多维响应模型,对不同灰色模型的预测精度进行了研究,主要结论如下:
1)基于GM(1,1)灰色模型的一维响应预测模型能较好地模拟和预测航道开挖过程中土体和结构的变形,但预测精度随着预测个数的增加而减小,高精度预测值集中在原始序列之后的几个值中,越往后误差越大.
2)针对施工过程中初始阶段数据较少的情况,优化的等维灰数递补模型在小样本数据的情况下,能显著提高小样本灰色模型模拟的精度,应优先使用.
3)GM(1,n)模型在拟合桥墩墩顶沉降的过程中,前期精度相比GM(1,1)模型稍低,但在后期模拟精度相比GM(1,1)模型显著提高,实际变形预测过程中可综合考虑GM(1,1)模型和GM(1,n)模型以提高精度,降低工程风险.

