基于临界折射纵波递归定量分析的纯铁疲劳损伤无损评价

孟亦圆，林 莉，陈 军，金士杰，罗忠兵

(大连理工大学 无损检测研究所，辽宁 大连 116024)

金属材料广泛应用于石化、核电、航空航天等关键领域重大装备，在服役期间长期处于高温、高压等恶劣工况，易产生力学损伤，严重降低零部件的承载性能和可靠性，威胁运行安全。大量工程案例表明，疲劳失效是主要形式之一，其中早期损伤阶段(宏观裂纹形成前)约占整个疲劳寿命的80%[1]，材料表面/近表面又是裂纹萌生高发区。因此，若能够在疲劳早期对损伤进行有效评价，便可预警灾难，对确保重大装备的安全运行意义重大。

在众多无损检测方法中，超声检测技术凭借穿透能力强、对人体无害和易于现场操作等优势被广泛应用。常用的体波法利用超声波的衰减、反射、透射来评估尺寸与波长相当或更大的损伤(如裂纹)[2]。然而，诸如位错、滑移带等早期演变通常为纳米至微米尺度，远小于常用频率下的超声波长，检测难度大。虽然单一微尺度损伤对超声的响应非常微弱，但由于疲劳早期形成的微尺度变化弥散分布、数量众多，整体仍可能带来超声信号的变化。目前已有学者利用声衰减、声速等特征参量对损伤进行评价，例如Ohtani等[3]发现声衰减系数对低碳钢的疲劳损伤累积程度敏感，分别在疲劳寿命2%和90%处出现峰值。Hirao等[4]发现多晶铜的声衰减系数在疲劳寿命20%～40%之间出现峰值，声速整体呈下降趋势。Luo等[5-6]提出了将水浸聚焦超声与电子背散射衍射技术相结合的晶粒尺度疲劳损伤评价技术，在粗晶、弹性各向异性金属早期损伤评价方面迈出了一步。有关非线性超声的研究也得到重视，主要是利用材料中位错、微裂纹等对大振幅超声波的非线性响应表征缺陷，检测灵敏度较传统体波法明显提升[7]。然而，高的检测灵敏度使非线性超声对检测条件较为敏感，多次测量重复性差，用于现场复杂工况检测受限[8]。近年来，临界折射纵波(critically refracted longitudinal，LCR)得到广泛关注。不同于能量集中于表面一个波长内的表面波，LCR波能量渗透深度与检测频率相关，可覆盖近表面区域更大范围[9]，且平行于表面传播，能够检测表面及更大深度范围损伤。同时，LCR波对表面粗糙度不敏感[10]，适合于工程零部件现场检测。目前，已将其用于残余应力[11-12]和宏观缺陷检测[13]，但在早期力学损伤评价方面的研究才刚刚开始[14]。

如何提取反映早期微尺度损伤的超声特征参量并建立其与损伤之间的映射关系，是实现早期疲劳损伤评价的关键。超声信号具有短程非平稳特点，接收信息中也会掺杂各种干扰因素，因此对信号中反映损伤的信息提取就尤为重要。递归定量分析(recurrence quantification analysis,RQA)是一种对时间序列非平稳性和混沌性进行评估的信号分析方法，可利用反映高维相空间轨迹递归特征的递归图(recurrence plot,RP)进行定量描述，提取非线性系统特征[15]。该方法对时间序列大小及平稳性无特殊要求，抗噪能力强，结果直观，已用于混凝土、复合材料等缺陷检测[16-17]。

前期已尝试将LCR波用于工业纯铁早期疲劳损伤表征，发现波形的重复测试稳定性较常规超声脉冲回波法显著提升[14]。本研究在前期工作基础上，以工业纯铁低周疲劳损伤为研究对象，分析LCR波结合RQA评价损伤的可行性，探索基于多参数的早期疲劳损伤超声无损评价方法。

1 实验材料与方法

为了消除弹性各向异性和复杂组织对波传播的影响，采用组织简单、近似看作弹性各向同性的工业纯铁(太原钢铁(集团)有限公司生产)作为实验样品，化学成分如表1所示。同时考虑LCR波探头间距和传播深度，设计试样几何规格如图1所示。平行段宽度10 mm，长度15 mm，厚度5 mm。为消除样品中残余应力，首先进行去应力退火，然后进行表面打磨及机械抛光，获得平整光滑表面。利用MTS Landmark液压伺服测试系统对样品进行疲劳加载，采用应力控制模式，加载波形为三角波，加载频率为0.1 Hz，R比为-1，最大应力为160 MPa，使用平行试样分别加载1～1000周次不等，并测得断裂时对应寿命为16970周次。利用Olympus OLS-4000型激光共聚焦扫描显微镜对不同加载阶段的样品表面进行扫描，得到高分辨率的表面形貌图像。

表1 实验用工业纯铁的化学成分(质量分数/%)Table 1 Chemical compositions of industrial pure iron for experiment (mass fraction/%)

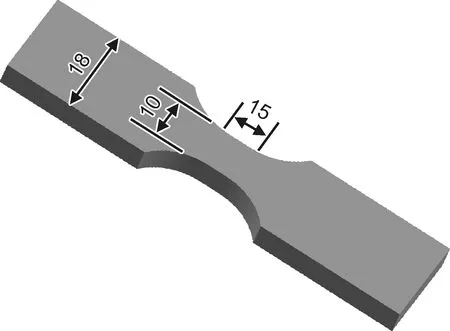
图1 纯铁疲劳实验试样几何示意图Fig.1 Geometric diagram of pure iron sample for fatigue loading

图2为搭建的LCR波测试系统。使用相同规格的C542型超声探头和有机玻璃楔块(纵波声速2730 m/s，入射角27.4°)发射和接收LCR波，利用5800PR超声脉冲发射接收器激励超声探头，DPO 4032数字示波器用于采集时域波形数据。为保证测试过程耦合条件一致，采用流动性好的水作为耦合剂，利用专用夹具控制探头与试样接触压力恒定。超声波首先倾斜入射至“楔块/试样”界面，折射后在试样内部产生的LCR波平行于试样表面传播至接收探头，从而实现表面/近表面疲劳损伤检测。

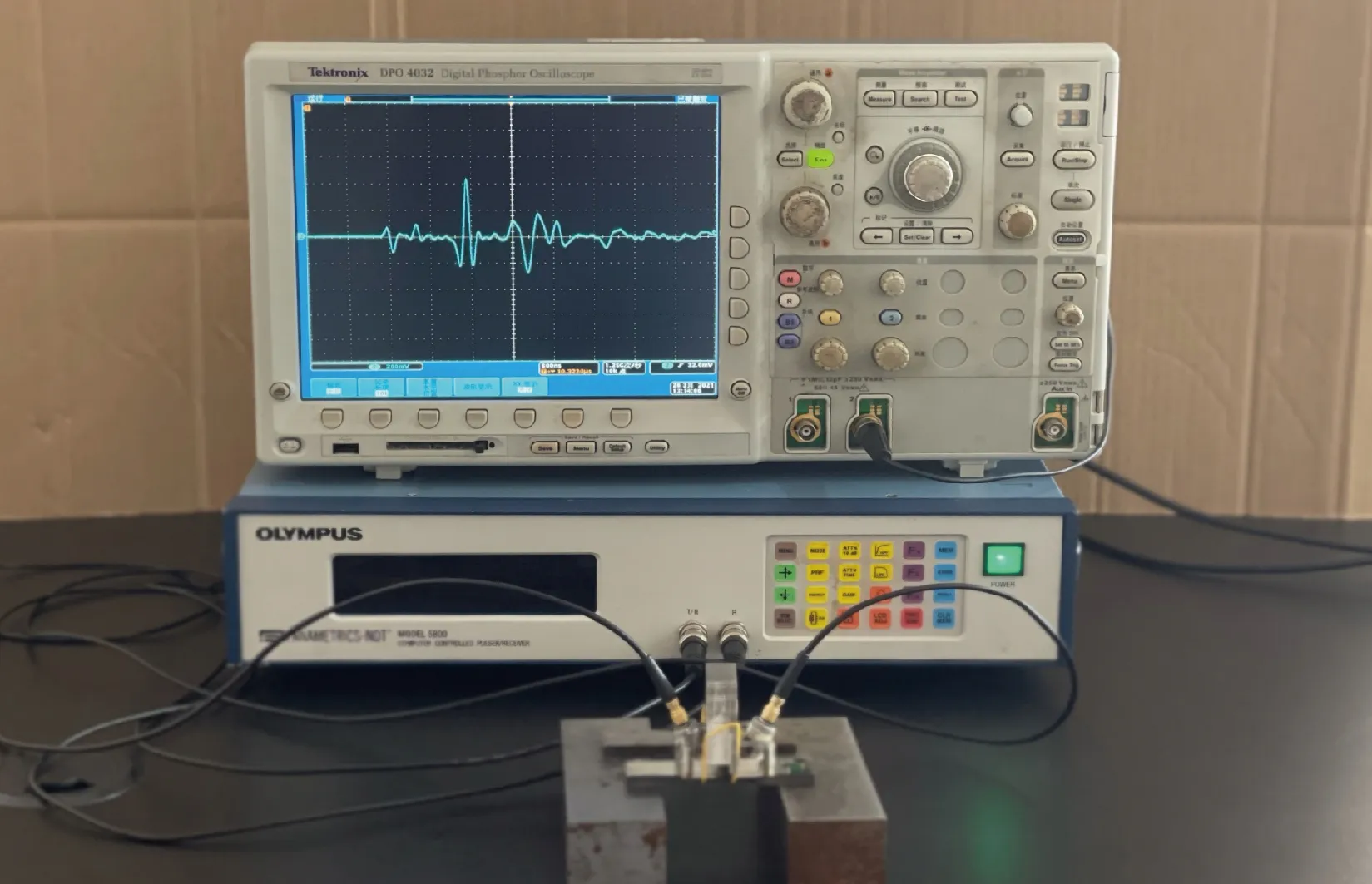
图2 LCR波检测系统示意图Fig.2 Schematic diagram of LCR wave detection system

2 结果与分析

2.1 纯铁循环响应及形貌演变

纯铁疲劳加载应变幅与疲劳周次之间的关系如图3所示。疲劳1～5周次对应的应变幅由1.8%快速下降至0.7%，表现为快速硬化。说明随着位错密度增加，位错间交互作用增强，位错塞积、缠结等致使其运动困难[18-19]。100周次以后依然保持硬化趋势，应变幅逐渐降低并趋于平稳。有关纯铁及20碳钢的相关研究表明[20-21]，因为体心立方金属层错能较高，位错交滑移容易发生，初始循环加载后，逐渐形成位错缠结和位错脉络，位错密度显著增加，个别条件下甚至会形成亚晶结构，导致宏观应变幅下降并趋于稳定。

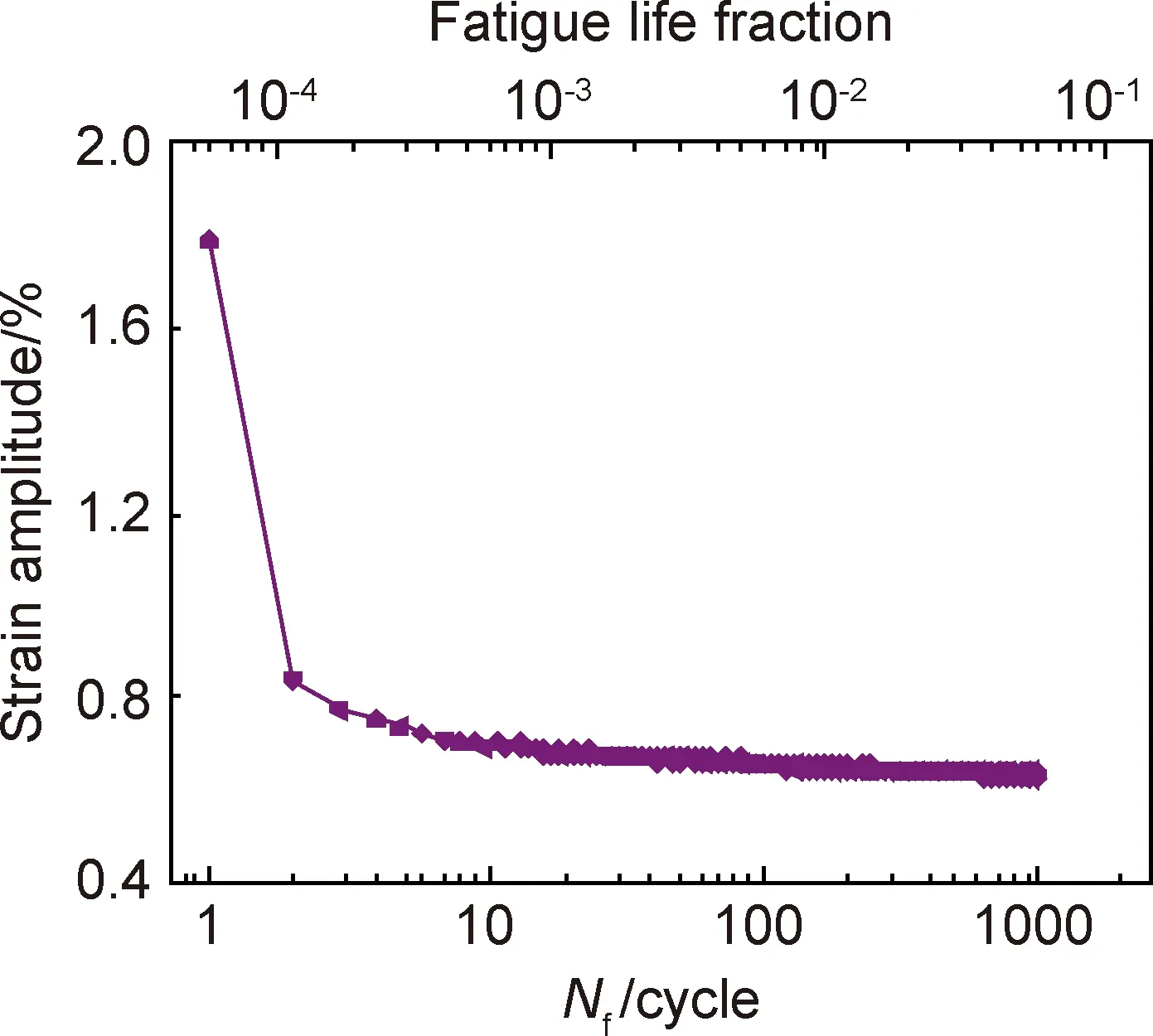
图3 应变幅随疲劳加载周次的变化规律Fig.3 Variation of strain amplitude with fatigue loading cycles

图4为不同加载周次下试样表面形貌激光共聚焦观测结果。可以看出，表面起伏程度随疲劳加载逐渐增大，其中0周次时试样表面为抛光后的平整状态，晶粒形貌清晰，见图4(a)；至2周次时，在少量晶粒内部发现相互平行的滑移带,如图4(b)所示；100周次时表面出现一定程度起伏，一些滑移带穿过晶粒并带动周围晶粒开始滑移变形，个别晶粒内部出现交叉滑移带，说明多个滑移系开动。此时，晶粒变形不均匀的现象更加明显，易于变形部位出现明显的挤入沟和挤出脊，如图4(c)所示；加载至500周次以后，表面出现凹凸不平的褶皱，如图4(d),(e)所示，几乎所有晶粒均发生严重变形，伴随着波浪状滑移线的出现。

图4 不同疲劳加载周次下纯铁试样表面形貌 (a)0周次；(b)2周次；(c)100周次；(d)500周次；(e)1000周次Fig.4 Surface morphologies for pure iron samples at different fatigue loading cycles(a)0 cycle;(b)2 cycles;(c)100 cycles;(d)500 cycles;(e)1000 cycles

2.2 纯铁疲劳损伤的LCR波评价

对疲劳加载0，2，100，500，1000周次的试样进行检测，计算其塑性应变分别为0%，2.5%，2.9%，3.6%，4.2%。发射探头激励超声波经过楔块折射进入试样，以LCR波、其他模式的波及多次反射波进行传播[22]，其中，LCR波传播距离最短，声速约是横波两倍，因而总是最先出现，在实验采集的时域波形信号中可与其他模式的超声波明显区别开来。图5分别是使用中心频率2.25,5 MHz探头采集的LCR波时域波形。对比图5(a),(b)可以发现，两频率下的LCR波幅值均随疲劳加载周次增加逐渐降低，且2.25 MHz条件下的幅值始终大于5 MHz条件，说明疲劳损伤会加剧超声衰减，且高频成分衰减程度更大。

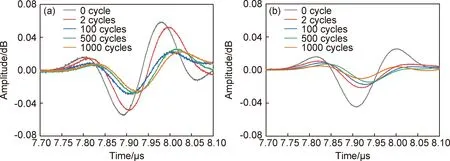
图5 不同疲劳加载周次下纯铁试样LCR波时域信号波形 (a)2.25 MHz；(b)5 MHzFig.5 Time-domain waveform signals of LCR waves for pure iron samples at different fatigue loading cycles(a)2.25 MHz;(b)5 MHz

由于测试过程易引入其他干扰，仅凭LCR波幅值大小难以准确评价损伤程度。为更好表征由疲劳损伤引起的LCR波幅值“净变化量”，以试样初始态为参比，定义损伤试样的LCR波归一化幅值差Adif：

Adif=|A0-AN|/Amax

(1)

式中：A0和AN分别为参比和损伤试样的LCR波幅值，N为疲劳加载周次；Amax为所有测试条件下幅值最大值。Adif越大，表明损伤程度越大。相应LCR波Adif变化规律如图6所示。2.25 MHz条件下，随着疲劳周次增加，Adif逐渐增大，1000周次时增至54%。相同条件下，5 MHz条件Adif更大，加载2周次时Adif增幅达52%，加载至1000周次时，Adif增幅达76%。这表明LCR波对疲劳损伤的灵敏度随频率增大而增加。对比发现，2.25 MHz下Adif随疲劳周次增加呈近似线性递增关系，5 MHz条件下Adif在疲劳初期(2周次)呈迅速上升趋势，而后缓慢递增。由图4(a),(b)试样表面形貌可知，2周次试样表面较平整，只在少量晶粒内部发现平行滑移带，损伤程度较低。2.25 MHz的LCR波波长较大，对上述微观疲劳损伤敏感度低，所以相应Adif较初始状态仅增加10%。相比之下，5 MHz条件LCR波波长更小，可以更早感应到位错结构变化，Adif增幅达52%。由图4(c)～(e)可知，加载后期试样表面因晶粒变形愈加粗糙，可能对LCR波产生一定程度散射，由此在后续加载至1000周次时增加趋势较初期缓慢。Langenberg等[10]推测LCR波对表面粗糙度不敏感，但综合5 MHz和2.25 MHzAdif结果，很难排除表面质量对声传播的影响，相关机理有待下一步深入研究。

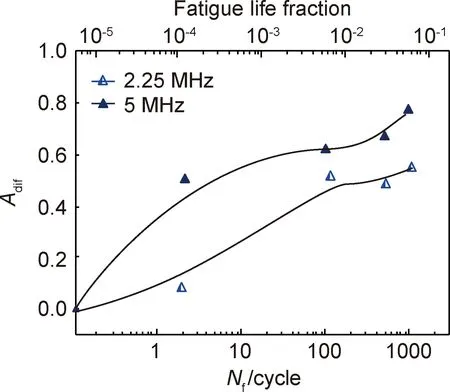
图6 纯铁试样LCR波归一化幅值差Adif随疲劳加载周次的变化Fig.6 Variation of normalized LCR wave amplitude difference Adif with fatigue loading cycles for pure iron samples

值得一提的是，传统脉冲回波法主要根据底面反射回波幅值计算得到声衰减系数进而评价损伤程度，所以试样必须具有足够大厚度以避免波形混叠对回波幅值测量带来的干扰。此外，该方法测得的声衰减系数随损伤程度变化并不单调，多呈“单峰”或“双峰”关系[3-4,23]，这就表明相同声衰减系数可能同时对应多个损伤程度，不利于损伤评价。相比之下，LCR波Adif随疲劳损伤程度单调递增，更有利于反向评价材料损伤程度；通过单侧一发一收即可实现LCR波的激励和接收，无须采集底面回波，不以试样厚度为先验信息，对密封构件现场检测颇具价值。

2.3 基于RQA方法的疲劳损伤评价

为提取超声波信号的稳定特征，对图5所示LCR波信号进行RQA分析。应用延迟嵌入定理[24]，将一维时间序列{xi}(i= 1, 2,…,N)进行重构，获得多维相空间X：

X=[X1,X2,…，Xi,…，XM]=

(2)

其中，第i个向量Xi表示m维空间中的一个状态，它构成相空间中的一个相点；τ为延迟时间；m为嵌入维数；重构后的相空间矢量数为M=N-(m-1)τ个。计算重构相空间中两个不同状态向量间距离，根据预设阈值构建递归矩阵：

Ri,j=Θ(ε-‖Xi-Xj‖)

(3)

式中：ε为预设阈值；‖Xi-Xj‖表示欧氏距离；算子Θ(x)为Heaviside函数。

将递归矩阵图像化得到RP图，规则为：Ri,j=0或1分别表示RP图(i,j)位置点为白色或黑色，即通过白点和黑点描绘图形来反映待研究时间序列特性，结果如图7所示。递归点大多平行主对角线分布，说明相点的运动轨迹彼此相似且逐渐逼近，即存在规律的递归点占大多数，LCR波信号可预测性好。随疲劳周次增加，RP图中黑色区域面积逐渐增大，递归点数量逐渐增多。两超声检测频率下的递归表现形式，即递归点的分布情况有所不同：2.25 MHz递归图中除主对角线外多为短对角线结构，随损伤程度增大，主对角线逐渐粗化；5 MHz递归点汇聚于右上角，形成的块状图形面积随损伤发展逐渐递增，主对角线粗化更加明显，非均匀程度增加，表明不同频率LCR波对损伤的响应特征存在差异，RP图可以直观表现疲劳损伤导致的信号递归特性变化。

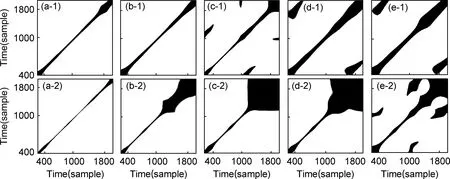
图7 纯铁试样在不同疲劳加载周次下2.25 MHz (1)和5 MHz (2) LCR波信号RP图(a)0周次；(b)2周次；(c)100周次；(d)500周次；(e)1000周次Fig.7 Recurrence plots of 2.25 MHz (1) and 5 MHz (2) LCR waves for pure iron samples at different fatigue loading cycles(a)0 cycle;(b)2 cycles;(c)100 cycles;(d)500 cycles;(e)1000 cycles

选用递归度(recurrence rate, RR)作为损伤参数，即RP图中黑色点(递归点)所占的比例，定量描述RP图随疲劳损伤程度的变化规律，结果如图8所示。随损伤程度增加，两频率条件下RR都呈增大趋势。2.25 MHz条件初始态试样RR为0.05，当加载1000周次时，RR达到0.17；5 MHz条件RR由0.02逐渐增至0.23，增幅高于2.25 MHz条件，大小关系同上述LCR波Adif情况。为与Adif对比，参照LCR波Adif的定义方式定义归一化RR差，如式(4)所示：

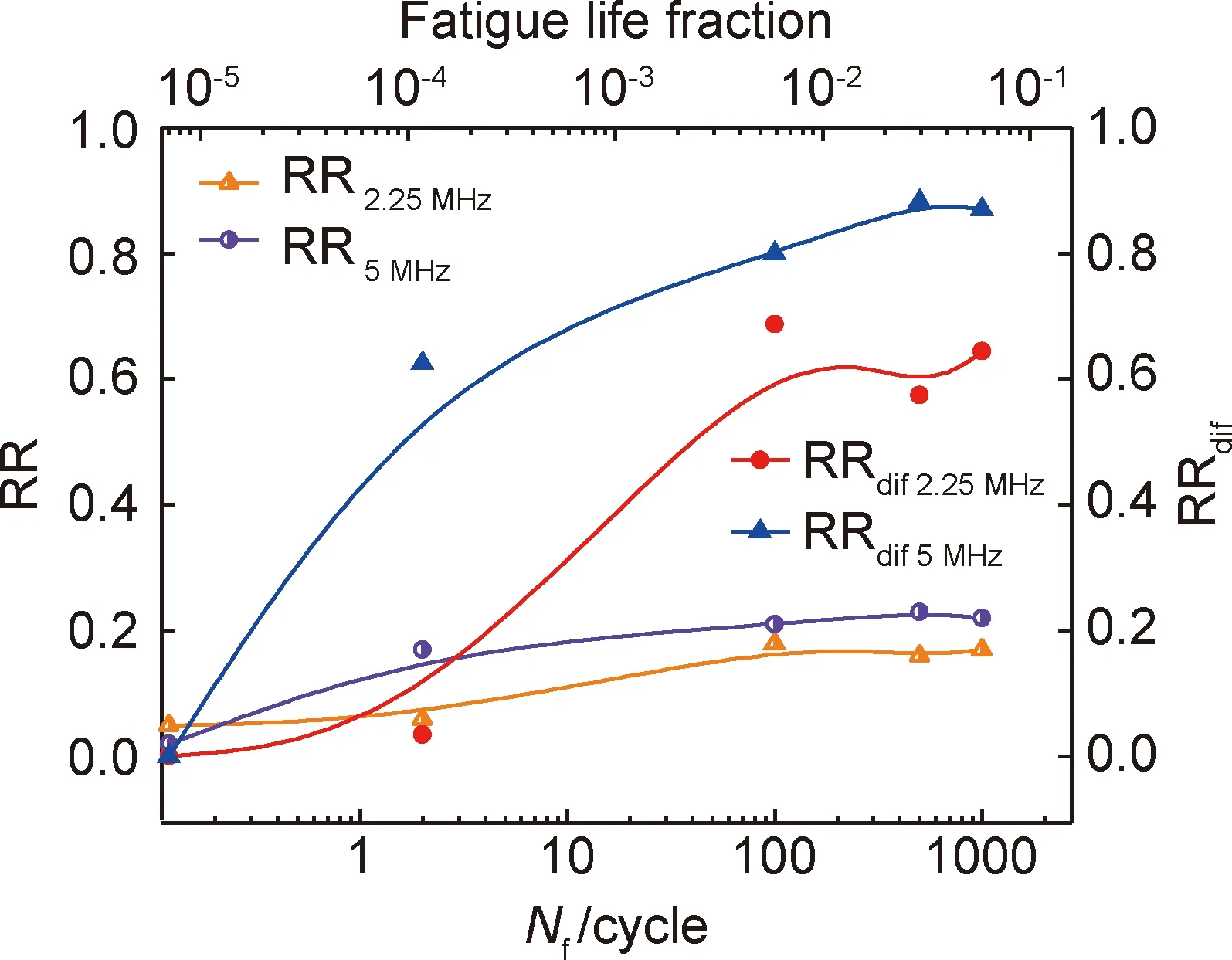
图8 纯铁试样LCR波递归度(RR)和归一化RR差(RRdif)随疲劳加载周次的变化Fig.8 Variation of recurrence rate (RR) and normalized recurrence rate difference (RRdif) of LCR wave with fatigue loading cycles for pure iron samples RRdif=|RR0-RRN|/RRmax

(4)

式中：RR0和RRN分别为参比和疲劳损伤试样的RR值；RRmax为所有测试条件下RR最大值。由图8可知，RRdif随加载周次的变化趋势与Adif基本一致，前者灵敏度更高。例如，2.25 MHz的RRdif变化率较Adif提升了10%，5 MHz条件提升更为明显，500周次时最大可达21%。进一步分析RQA对疲劳损伤的敏感程度，引入频域、时频域方法进行对比，采用快速Fourier变换(fast Fourier transform, FFT)与短时Fourier变换(short-time Fourier transform, STFT)对5 MHz频率下LCR波进行处理。对应FFT表达式为：

(5)

式中：x(t)为某一瞬时态信号；ω表示角频率。可观察有效频带范围内，不同频率成分超声对疲劳损伤的声学响应程度差异，将信号的幅值以频率坐标表示，从而分析信号的频率特征。

对于给定信号x(t)，STFT定义为：

(6)

式中窗函数h(τ-t)将信号限制在分析时间τ=t附近输出，是信号x(t)在时间t附近的局部频谱。窗函数h(τ-t)随时间移动，用于分析各频率成分随时间变化的过程。提取LCR波信号经FFT所得幅度谱的最大峰值作为频域分析结果，经STFT所得时频分布图的最大幅值作为时频域分析结果。参照式(1)进行归一化处理，将2.2节所得Adif作为时域分析结果一并示于图9。4种方法对应指标随损伤程度发展均呈单调递增关系，其中：时频分析最大幅值的敏感度最低，时域、频域两方法的敏感度居中且大小相近，RQA方法灵敏度最高，较时域、频域方法提升约20%，较时频域方法提升约44%。Nichols等[25]将RQA方法用于钢板的裂纹损伤评价，发现RR较板结构模态频率对损伤更为敏感，证实RQA方法在损伤评价方面的优越性，与本实验结果吻合。

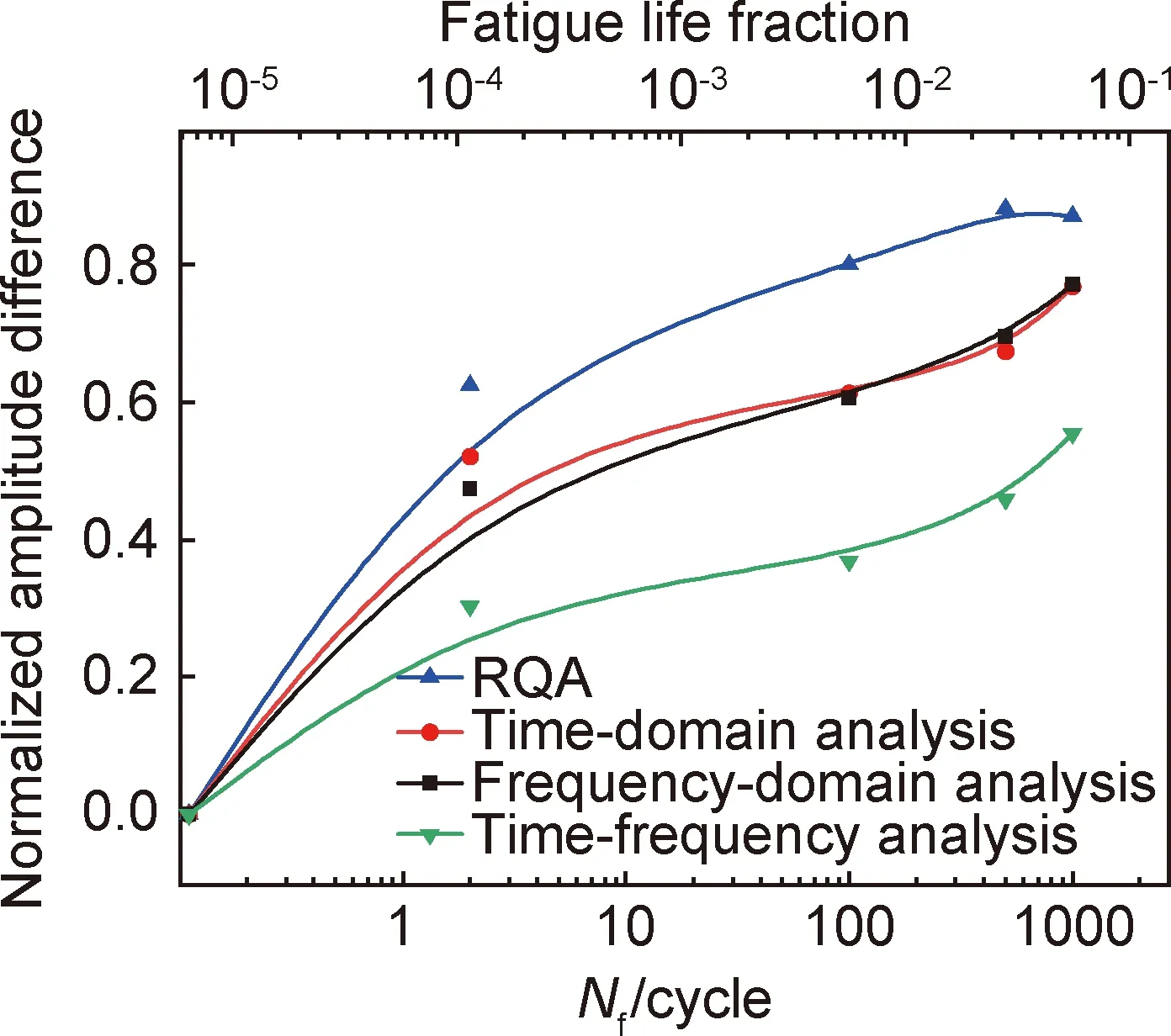
图9 纯铁试样LCR波RQA结果与时域、频域、时频分析结果对比Fig.9 Comparison between RQA and analysis results of time domain,frequency domain and time frequency for LCR wave of pure iron samples

已有研究表明，疲劳变形过程伴随位错、晶界、微裂纹等演变[18-21,26-27]，不同损伤形式之间具有跨尺度、强耦合特点，分布位置不确定，各自引起的超声响应也不相同，因而可将超声波在疲劳试样中传播过程视为复杂的非线性系统。例如，位错阻尼效应可导致声衰减、声速变化[3-5,23]，晶界作为声阻抗失配界面，会导致散射衰减和多重反射[28]；微裂纹与超声波之间作用机制更为复杂，同时出现散射、衍射、非线性效应、波模式转换等[3,7]；表面粗糙度也会导致超声衰减和非线性效应[8]。上述不同类型损伤与波的作用体现为系统的非线性和复杂性，并进一步影响接收信号的动力学行为。RQA方法作为非线性时间序列的分析工具，从结构动力学角度捕捉全局信号特性变化，反映疲劳损伤信息，较常用时域、频域、时频域等线性方法对早期损伤敏感性更强(见图9)，所以利用RQA处理LCR波能够更加全面评估材料性能变化，进而实现损伤程度的多参数定量表征。相关研究为金属材料的早期疲劳损伤评价提供了探索空间，并在其他材料损伤研究中具有推广价值。

3 结论

(1)工业纯铁在应力控制拉-压疲劳过程中表现为循环硬化，应变幅初期快速降低并在后期逐渐稳定。原因在于体心立方结构层错能较高，位错容易交滑移，加载初期位错迅速增殖、密度显著增加，并在继续加载过程中逐渐形成位错脉络，导致应变幅下降并趋于稳定。

(2)随疲劳加载周次增加至1000周次，LCR波幅值及对应归一化幅值差Adif整体呈单调变化，5 MHz条件灵敏度高于2.25 MHz条件，更有利于评价疲劳损伤程度；分析认为主要体现为位错的阻尼效应，并可能与粗糙表面散射有关。

(3)对不同疲劳损伤试样的LCR波信号进行递归定量分析，递归图可直观区分不同频率、不同损伤状态下信号差异，损伤指数归一化递归度差RRdif与疲劳加载周次之间呈单调递增关系。与常用时域、频域、时频域分析(如最大幅值法)相比，递归定量分析方法灵敏度明显提升，幅度可达44%。因此，基于LCR波信号递归定量分析能有效评价早期疲劳损伤，为相关研究提供了新手段。