基于加权图传播最优化的网络社区检测算法

张 政， 单平平， 韩义波

(1.南阳理工学院计算机与软件学院 河南 南阳 473000；2.南阳理工学院南阳大数据研究院 河南 南阳 473000)

0 引言

随着社交网络中数据的爆炸性增长，越来越多的研究者开始关注网络中的特征建模与分析，其中最有价值的结构特征是网络中的社区结构[1]。社区是指各种密集的子模块，之间存在着稀疏的连边关系，而同一社区内的节点之间的连接关系往往更为紧密[2,3]，即社区是高度互连的节点集合，社区边缘的连边相对稀疏。网络中的社区结构检测在真实场景下有着巨大的应用价值，例如病毒式营销的追溯、传染病预防和推荐系统相似人群识别等[4]。

现有多数社区检测算法试图利用网络拓扑结构数据来检测社区划分。但是，在真实的社交网络中有着严格的隐私和保护政策，获取完整的网络拓扑结构是不可行的，这就直接影响了现有算法的性能和扩展性。除此之外，这些基于网络拓扑结构的方法难以捕获社区节点之间的行为特征、偏好兴趣等动态数据，而这些特征对于社区结构的分析又是十分重要的[5-7]。

利用网络中的传播扩散数据追溯面向社区的传播过程可以有效解决上述问题。其中推理图算法首先通过传播扩散数据推断估计底层网络的拓扑结构，进而基于图的分簇算法来获取社区划分，这类算法取得了不错的检测效果。但是这类方法存在着计算复杂度过高的问题，并且多数推理图算法需要底层网络的边数参数来优化检测结果的性能[8]。因此，本文在社区检测算法中直接利用了信息传播的级联数据，其中，级联是网络中节点参与传播形成的可追踪路径，包括了节点基础信息和加入级联的时间，在一定程度上揭示了网络中节点的行为特征，利用构建的加权图和传播似然最大化优化方法，得到网络中的社区划分结果。最后，通过大量的实验证明了所提算法在检测效率和准确度方面相比现有算法有明显的提升。

1 相关工作

1.1 社区检测算法

在基于网络拓扑结构的社区检测算法中，Barbieri等人[9]利用网络拓扑结构实现社区检测，并使用级联信息对检测到的社区进行优化，以得到更接近真实划分的社区结构。Himel等人[10]则是从社交网络中用户的交互(分享的照片、影片或者评论转发)即传播级联中创建了一个加权图，然后利用网络拓扑结构中每对节点之间的共同邻居创建了关联图，最后基于加权图和关联图的分层分解与合并操作，检测出隐藏的社区结构。另外在基于社区结构实现影响力最大化传播方面，也涌现出许多优秀的方法。扩散感知网络推理算法(Diffusion Aware Network Inference Algorithm，DANI)[11]尝试利用传播级联中节点的感染时间来推断网络拓扑结构。NetInf算法[12]基于流行病模型，对每个传播级联构建出现概率最大的传播树。MultiTree算法[13]在NetInf算法上进行了优化，保留了传播级联对应的所有可能的传播数，实验证明在级联数较少的情况下，能获得更优的性能。NetRate算法[14]利用似然优化问题的凸特性，对网络中的传播数据进行建模优化，最终推理图社区划分。在列举的这些网络推理算法中，DANI在推理过程中可以很好地保留社区结构特征，因此有着最优的检测效果。但是推理图算法有一个共同的局限性是需要预先知道所在网络的连边数，并且生成推理图和社区检测两个阶段都有着很大计算复杂性。

Barbieri等基于NetRate算法和独立级联模，将网络节点之间的扩散影响优化为社区对节点信息传播的影响，提出了C-Rate和C-IC网络推理模型，在不需要知道网络拓扑结构的情况下进行社区检测，不同级联中节点的感染时间和社区数量是该算法唯一需要的先验信息，但是，该算法执行效率低，大网络数据上的性能比较差。Maryam[15]利用传播级联数据中的马尔可夫属性，提出了一种基于最大似然优化的CoDi算法，将级联中的节点作为输入，根据节点对共同参与级联的概率计算节点对的相似性权重来实现社区结构的检测。

1.2 影响力传播模型

本文提出的社区检测算法是基于网络中信息传播的级联数据，而对于合成网络和大部分的真实网络并没有现成的传播级联数据，需要选取符合真实传播规律的传播模型[16-18]。而影响力传播中经典的两个模型是独立级联模型(Independent Cascade Mode，IC模型)[19]和线性阈值模型(Linear Threshold Model，LT模型)[20]。

IC模型属于概率模型，其信息传播的过程为：(1)给定初始活跃节点集合S，当在时刻t节点v被激活，以概率P(v,w)对未被激活的邻居节点w尝试激活，尝试激活行为执行一次，并且相互独立，概率值越大，节点w越有可能被激活。(2)如果节点w有多个邻居节点是最近被激活的，那么这些节点随机尝试激活节点w，当节点v成功激活节点w，那么在t+1时刻，节点w为活跃状态。(3)在t+1时刻，节点w将对其邻居节点尝试激活，以此重复上述过程。需要注意的是，在传播过程中，在时刻t无论节点v是否成功激活其邻居节点，在下一时刻后，节点v虽然保持活跃状态，但不具备激活其他节点的影响力，这类节点为无影响力的活跃节点，当网络中不存在有影响力的活跃节点时，传播结束。由于IC模型的激活过程是不确定的，在同一网络上，相同种子节点集合进行传播的结果差异较大[21,22]。

LT模型属于价值积累模型，对于每个节点v都有一个激活阈值θ[v]∈[0,1]，其信息传播过程为：(1)给定节点集合中的任意节点v随机分配阈值θ[v]∈[0,1]，该阈值表示这个节点受影响的难易程度，只有当节点v的最新激活态邻居节点对其的影响力大于该阈值时，节点v才能被激活。(2)权重b[w,v]表示节点w对节点v的激活影响力，∑w∈in(v)表示节点v的激活状态的邻居节点对其的影响力，in(v)是节点v的入边邻居节点结合。(3)给定初始活跃节点集合S，对网络中每个节点设定一个随机阈值，在t时刻，节点v的所有活跃邻居节点的影响力之和大于节点v的阈值时，节点v被激活。(4)节点v被激活后，下一时刻对其邻居节点产生影响，重复上述过程。在LT传播模型中，当网络中存在的所有活跃节点中任意活跃节点的影响力之和都不能激活处于非活跃状态的邻居节点时，传播过程结束。相比于IC模型，LT的激活过程是确定的[23]。

为了从IC模型和LT模型中选取最符合真实传播规律的一个，分别以最优参数在节点数为1000的LFR(Lancichinetti-Fortunato-Radicchi)合成网络上运行两种传播模型，对比模型生成的级联分布，符合长尾分布的模型更加接近真实的网络传播。如图1所示，IC模型的级联长度更符合长尾分布，因此在随后的实验中选取IC模型模拟生成网络中的信息传播级联数据。

2 基于加权图传播最优化的N-CD算法

N-CD算法不需要网络拓扑结构作为先验信息，直接从传播级联o={o1,o2,...,om}中将网络中的节点V={v1,v2,...,vg}划分到不同的社区，每个级联oi都是信息i在网络G中的传播轨迹，oi表示第i个级联中的节点及其感染时间oi={(v1(i),t1(i)),(v2(i),t2(i)),...,(vg(i),tg(i))}。当节点j没有出现在第i个级联时，那么该节点在第i个级联中的时间t为∞，并定义参与级联的节点为活跃节点u，U表示活跃节点集合，N-CD算法假设有k个不同的社区，对于每个活跃节点u，找到其最可能的社区分配Y(u)={1,2,...,k}。因此，社区检测任务转化为基于传播级联o，在网络中求解出社区分配Y，使得P(Y|O)最大化，公式为

(1)

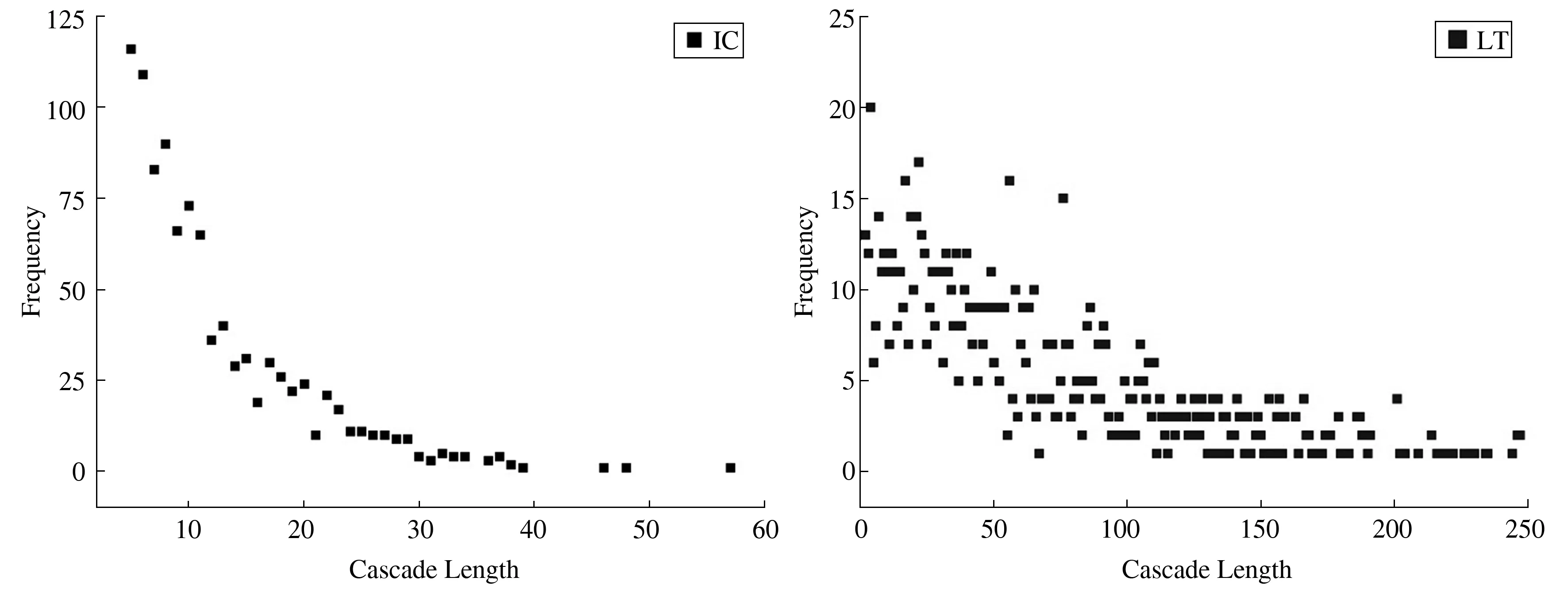
图1 IC模型和LT模型的级联长度分布对比

2.1 条件随机场CRF

在一个具有社区结构的网络中，如果N{i}代表节点i的邻居集合，且当节点i至少有一个邻居节点被分配到某社区时Y(N{i})=a，那节点i就属于社区Y(i)=a。该网络满足马尔科夫属性(Markov Property)[24]：在一个无向图G中，对于任意节点i，其社区标签只由其邻居节点的社区标签决定，具体公式为

P(Y(i)|Y(U-{i}))=P(Y(i)|Y(N{i}))

(2)

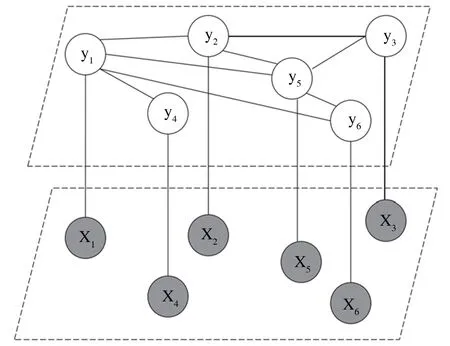
图2 CRF表示6个节点构成的网络

这里，可以利用条件随机场对公式(1)中的概率模型进行建模。条件随机场是一种用于表示观察到的随机变量X和隐藏变量Y的条件概率P(Y|X)的无向图模型，有两个特性：(1)G=(U,R)是一个无向图，它的每个节点i都有一个对应的社区标签y(i)，节点i和节点j之间的相似性由一条边rij∈R来连接。(2)满足马尔可夫的属性。CRF表示如图2所示。

在CRF中，假设有m个不同独立级联在网络中传播，那么图中的随机变量定义如下。

X：为每个节点Xi定义为1×m的向量，表示在级联中观察到的节点，如果节点i参与了级联Oj，则向量中第j个元素设为1。

(3)

Y：作为隐藏随机变量表示节点所属的社区划分，y(i)∈Y。

G=(U,R)：根据节点向量X之间的相似性构建的加权无向图，节点集合为活跃节点集合U。在网络传播过程中，同一社区内的节点间相互影响的概率更大，因此基于节点间传播行为的相似性，检测节点间可能存在的连边。依据此，假设节点i和节点j参与同一条级联，那么节点i和j之间存在一条边rij(rij∈R)，即节点i和j互为邻居节点，利用余弦相似性定义边权重，表示节点间传播行为的概率

(4)

由于余弦相似性度量的对称性，此加权图为无向图。同时，通常情况下级联的长度比较短，那么加权图中的节点邻居较少，对应的邻接矩阵比较稀疏。综合以上两个特性使得余弦相似性的计算速度更快。通过引入条件随机场CRF，公式(1)转换为

(5)

2.2 Gibbs分布

为了定义条件概率分布P(Y|X)使得公式(5)中的随机向量Y最大化，这里我们利用Hammersley-Clifford定理[25]来实现。

Hammersley-Clifford定理：当且仅当概率分布函数可以被定义为Gibbs分布时，随机场P(Y|X)才是一个条件随机场，即此定理认为Gibbs分布和条件随机场的属性是一致的。利用此定理，随机场P(Y|X)建模为Gibbs分布

(6)

其中T(X)是归一化因子，exp部分表示节点的社区权重，b表示所有边的加权和，rij表示节点i和节点j之间边的权重，ri和rj是节点的加权度，I为

(7)

将公式(6)代入公式(5)并消除负号可得

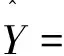
(8)

2.3 最大似然估计

针对公式(8)的最大似然估计问题，考虑优化计算的效率，从概率图模型推理的角度对最大似然估计问题进行优化，我们采用一种求解基于指数分布的马尔可夫模型导数关系的算法，通过贪婪策略更新模型中涉及的变量，直到节点所属社区权重收敛为最优值，具体求解步骤如下。

(1)社区标签的初始化。为每一个活跃节点赋予离散值为{1,2,…,k}的社区标签来完成社区的初始化划分。

(2)社区标签的更新。对于节点i，根据其邻居节点j来计算社区权重，当完成节点i所有邻居节点社区权重的计算后，选择社区权重最大的社区标签yj作为节点i的社区标签。

(3)迭代过程中止。经过社区标签的n次迭代更新后，算法会收敛得到一个社区划分Y(n)，当Y(n)与上一轮迭代得到的社区划分Y(n-1)之间没有显著的变化，则算法迭代结束。这里的Y表示社区标签向量，因此不能使用欧式距离作为判断收敛的标准，我们利用纯度度量[1]定义了一个Diff函数，来表示Y(n)和Y(n-1)的距离，即为社区划分Y(n)和社区划分Y(n-1)之间节点社区标签改变的比例，当Diff函数的计算值低时，表明社区划分已经收敛。其中，Diff函数公式为

Diff(Yn,Yn-1)=1-purity(Yn,Yn-1)

(9)

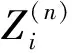
(10)

N-CD社区检测算法利用条件随机场对信息传播的级联数据进行建模，构建出对应的加权图和随机变量，然后应用迭代条件优化算法，得到所有活跃节点的最优社区划分向量Y，N-CD算法的伪代码如表1所示。

表1 N-CD社区检测算法

2.4 社区数优化估计

为了解决社区划分数量的先验条件和最优社区数估计问题，我们继续在所提出的N-CD算法的基础上进行优化估计。首先，将社区数设置为一个常数K，然后线性迭代更新直至满足迭代终止条件。对于每一轮迭代的kt值，执行N-CD检测算法计算出社区划分Ct，并线性增加K的取值，通过计算两个连续社区划分Ct和Ct+1的归一化互信息(NMI)放入数组Z中，当Z[t]达到局部最大值，则输出社区Ct(如表2)。

表2 社区数优化估计算法

3 仿真实验与结果分析

3.1 实验数据集

本文采用LFR模型[26]生成合成网络，LFR模型是一种用于验证社区检测的基准生成图算法，由如下参数来控制合成网络生成的过程：节点数n，平均节点度k，最大节点度max_k，度幂律分布指数β，社区规模的幂律分布指数γ，最小社区规模min_c，最大社区规模max_c，混合参数μ。首先，根据参数β和k生成每个节点的度，其次为每个节点生成边，其中连接到同一社区中节点的边比例为1-μ。然后，根据参数γ生成每个社区的规模，并满足所有社区规模大小的综合等于参数n。最后为每个节点分配所属社区并满足设定的节点度属性和混合参数。在实验中设定参数：n=1000,k=15, max_k=50,β=2,γ=1, min_c=20, max_c=50。由于混合参数μ直接决定了网络中社区结构的区分度，因此本文将参数从0.05改变为0.5，从而生成10中不同的合成网络(S1-S10)。当参数μ较小时，不同社区很好分离，当μ较大时，网络中的社区相互重叠。

Twitter数据集包含了2010年9月至11月爬取的真实Twitter数据[27]，Twitter数据集中的每条推文包含了哈希标签列表、推文原用户id和推文转发时包含的超链接数量，Twitter数据集中有2个确定的政治群体作为社区划分的标准。本文中我们根据推文的哈希标签列表、源用户id和超链接数作为判断唯一推文级联的标准对数据进行了预处理，最终得到的数据集包含18470个Twitter用户，31143条推文级联，级联平均长度为2.84956。

在博客数据中，当一个网站引用另一个网站的博客时，会产生一条传播级联，博客数据集收集了在2011年3月至2012年2月期间，以特定主题分类的近330万网站引用博客的数据[28]，本文整理了4种主题的引用级联数据，其统计结果如表3所示。

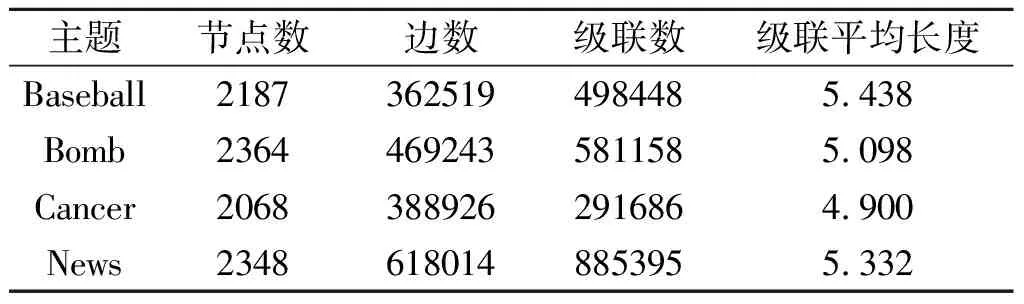
表3 带有传播级联的4种不同主题的博客数据集

3.2 算法评价指标

为了评估社区检测算法的性能，根据数据集的不同特征采用不同的评估指标。在带有真实社区划分的数据集上，我们可以通过将社区检测算法检测出来的社区结果与真实的社区划分进行对比来评估算法的性能。而在没有真实社区划分的数据集上，我们采用聚类算法的评价指标来验证所检测社区的质量。因此，根据数据集中是否带有真实社区划分，将算法评价指标分为如下两类：

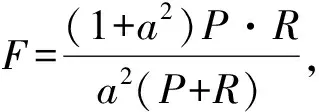
其中RI为Rand Index。Jaccard指标是比较有限样本间异同的度量[29]，其计算公式为

(2)聚类指标。在没有真实社区划分的数据集上采用评估聚类算法的指标来衡量社区划分的质量。其中模块度(Modularity)是衡量网络中社区稳定性的常用方法，其计算公式为

Conductance用来评估单个社区的紧密度，其计算公式为

Internal Density是社区中实际连边数与所有可能的连边数的比值。Cut Ratio是另外一种综合考虑社区内节点紧密度和不同社区内节点之间的松散度的有效度量方法[30]。

3.3 实验结果分析

3.3.1 LFR合成数据集的对比实验

为了对比社区检测算法的性能，通过改变混合参数μ，生成了10种不同的合成网络(S1-S10)，并采用IC影响力模型模拟产生信息传播级联数据。实验中每个算法分别在所有合成网络上运行5次，并计算相应评价指标的平均值，其对比结果如图3所示。

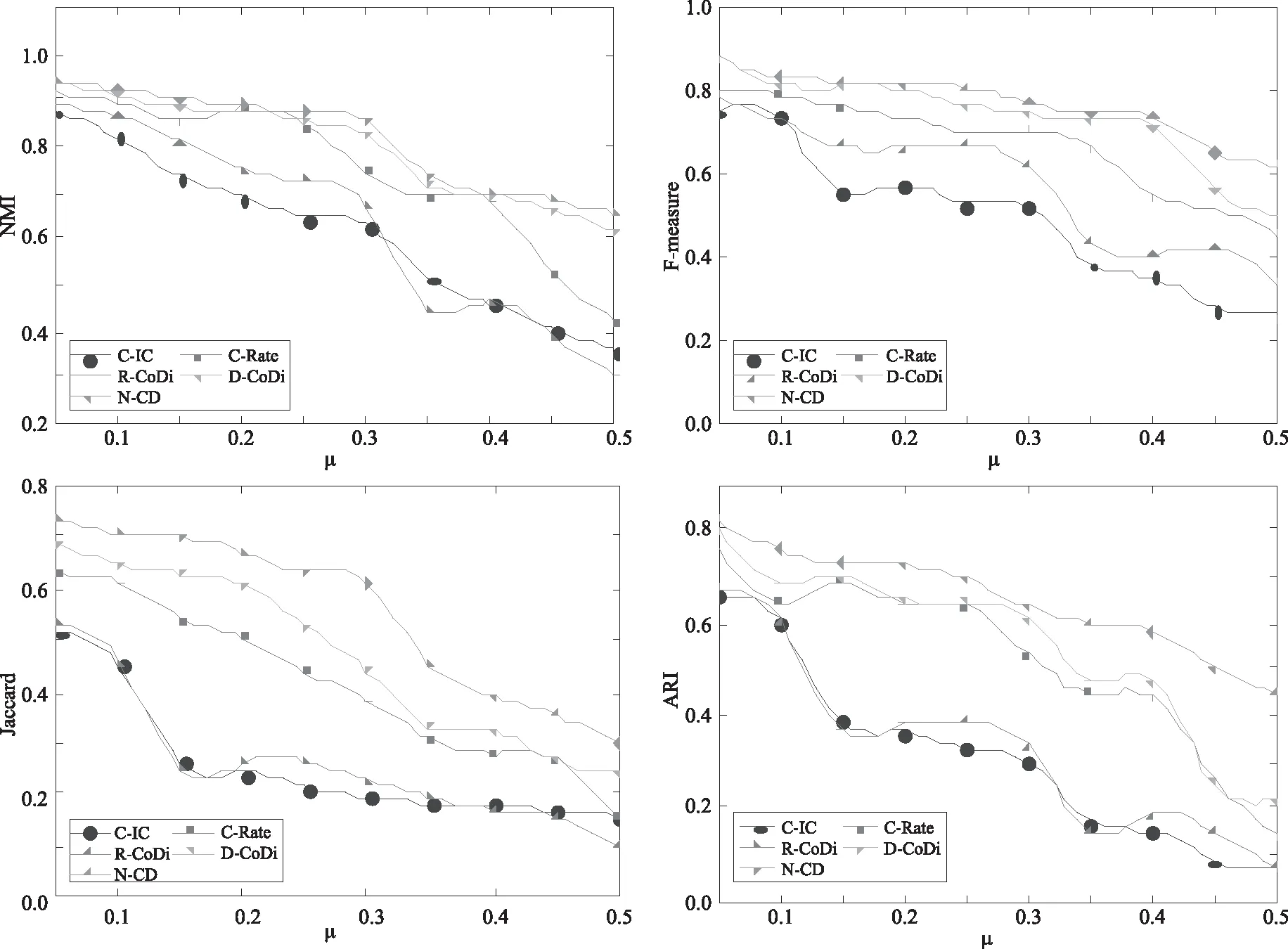
图3 LFR合成网络上的实验结果对比

从图3中可以看到，随着混合参数μ的增大，所有算法在4个评价指标上都有不同程度的下降，但在参数μ变化的过程中，本文提出的N-CD社区检测算法在所有4个指标上都优于其他基准算法。当μ>0.3时，合成网络中社区结构的划分并不明显，这对算法提出了极大的挑战，而N-CD算法在NMI和F-measure指标上的结果分别保持在0.65和0.62以上，说明了N-CD算法优秀的社区检测能力。在LFR合成网络中，真实的社区划分是已知的，实验中我们也将算法检测到的社区数量作为评估算法优劣的标准，对比结果如图4所示，本文提出的N-CD算法检测出的社区数量更加接近真实社区的数量，从另一个角度证明了该算法在社区检测方面的性能优势。由于C-IC和C-Rate算法需要以社区数量作为算法运行的先验知识，实验中使用了合成网络中的实际社区数量，因此C-IC和C-Rate检测出的社区数量必然是实际的社区数，对其他算法不公平。所以，将其排除在本组对比实验之外。3.3.2 Twitter数据集的对比实验

在Twitter数据集上包含有完整的真实社区划分和传播级联数据，实验中对比分析了所有算法在Twitter数据集的评价指标，实验结果如图5所示。文中提出的N-CD算法在4个不同的评价指标上稳定地表现出最好的性能，这与在LFR合成网络上的实验结果一致。由于一些评价指标存在不同程度的偏见性，比如对较大或较小社区的偏好等，而相比于其他基准算法实验结果的波动性，N-CD算法在社区检测任务上表现出较好的稳定性和识别精度。

由于博客数据集没有真实的社区划分，因此实验中我们采用另外一组聚类评价指标来对比社区检测算法的性能。其中，Modularity和Internal Density指标的高得分以及Conductance和Cut Ratio指标的低得分都能够体现社区检测的优异性能。基于博客数据集的不同算法的实验结果统计如表4所示。与其他基准算法相比，N-CD社区检测算法在4种不同主题的博客数据集上取得最高的Modularity和Internal Density指标值，以及最低的Conductance和Cut Ratio指标值，并且与最佳基准算法相比，在Modularity、Internal Density、Conductance、Cut Ratio等评价指标上的平均性能提升分别达到了51.73%、4.96%、40.41%、41.96%。虽然，实验中无法得到博客数据集中真实社区划分从而来评估算法所检测社区的质量，但是从社区聚类属性特征的评价来看，N-CD算法要显著优于其他基准社区检测算法。

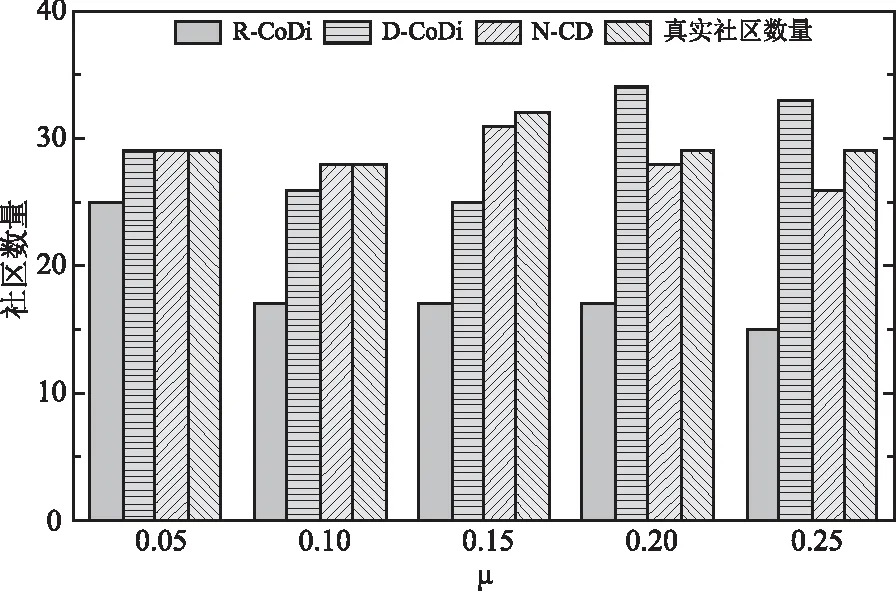
图4 LFR合成网络上检测的社区数量对比

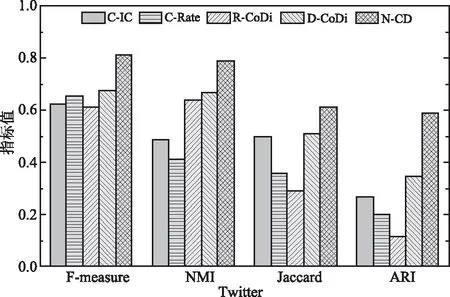
图5 Twitter网络上的实验结果对比

表4 带有传播级联的4种不同主题的博客数据集

4 结语

为了解决现有社区检测算法需要利用网络拓扑结构作为先验知识，从而严重影响算法扩展性和精确度的问题，本文利用网络中信息传播的级联数据，提出了一种基于加权图传播最优的网络社区检测算法N-CD，首先利用条件随机场对传播级联的时间序列进行建模，然后通过最大似然估计方法对构建的概率图模型进行优化推理，最终得到最优的网络社区划分。通过在LFR合成网络、真实的Twitter和博客网络上与其他4种社区检测算法对比分析，证明了所提算法在社区检测任务上的性能优势，不仅提升了检测的准确率和稳定性，并且对于评价指标的偏好波动有着更好的鲁棒性。