基于反熵权-AHP法的电力工程施工风险评价研究

俞 军， 张锦圣

(1.安徽建筑大学经济与管理学院 安徽 合肥 230022；2.合肥学院经济与管理学院 安徽 合肥 230601)

电力工程一般需要较长的建设周期，投入资金大，专业性强，管理也比较复杂，因此会不可避免地存在各种潜在的风险。当前，我国有关电力工程风险的研究主要集中在投资、生产、融资、招标、安全等方面，却没有系统全面地研究过施工单位在项目施工阶段面临的风险与威胁，致使施工单位在电力工程施工阶段中的风险管理比较薄弱，可供参考的体系较少。因此，对于电力工程施工风险的评价是很有必要的。

使用科学、准确的方法对风险进行评价，已经成为行业领域研究者关注的焦点。Mohammad Yazdi[1]提出了基于直觉模糊混合TOPSIS的风险评价方法，以优化风险矩阵的局限性和群体决策利用专家意见的不确定性。Shen Yuanshun等[2]提出了三阶段模糊综合评价模型，采用层次分析法确定各阶段因素的权重，采用模糊集方法确定隶属函数，并进行风险排序。Zhao Bin等[3]在二代曲波变换、人工神经网络和模糊理论的基础上，构建了模糊二代曲波神经网络风险评估模型。李立云等[4]引入灰色关联模型对层次分析法(AHP)进行融合改进，构建了基于灰色关联模型的改进型层次分析法的综合评价体系，通过组合权重值对基坑开挖的风险进行了评价。王景春、张法[5]提出一种熵权二维云模型的风险评价方法，同时提出风险云相近度的计算方法以确定风险等级。李万庆等[6]提出了基于AGA-AHP的模糊综合评价模型，运用加速遗传算法对层次分析法进行改进，再结合模糊综合评价法进行风险评价。段世霞、徐敏[7]运用结构方程模型方法，将定性与定量方法相结合，进行风险评价研究。贡力等[8]采用序关系分析法(G1法)和变精度粗糙集理论(VPRS)并结合最小信息熵原理(MIE)的权重确定方法，验证了多层次灰色评价模型对于风险等级的确定较为有效。宋战平等[9]将非线性算子引入到传统FAHP的综合计算中，建立了基于非线性FAHP的风险评价新模型。

从以上研究成果可以看出，国内外学者为使综合评价更为科学、准确，在综合评价过程中逐渐倾向于两种或多种评价方法的结合使用，这样既能够发挥不同方法的各自优势，又可以对彼此间的不足进行弥补。通过对电力工程施工风险指标特点的分析，本文决定选用反熵权-AHP法建立多指标综合评价模型，反熵权法用于客观权重选择，AHP法用于主观权重的选择，两者共同构成综合权重优选模型，主客观结合，相辅相成，然后再运用模糊综合评价法对电力工程施工风险进行评价。

1 电力工程施工风险评价指标体系建立

电力工程施工风险评价指标体系的建立，应遵循科学性、全面性、灵活性、可操作性、层次性、逻辑性、指标体系定性与定量相结合的原则[10]。本文采用文献分析法来建立风险评价体系，并结合了电力工程施工风险管理的实践经验，按照层次分析法构建的层级思路，将电力工程施工风险评价指标进行分解，总结出电力工程施工风险中的5个主要影响因素：环境风险、合同风险、经济风险、组织风险以及技术风险，这些因素为准则层指标。在准则层指标的基础上，再划分出17个二级评价指标因素，得出电力工程施工风险评价指标体系(如图1)。

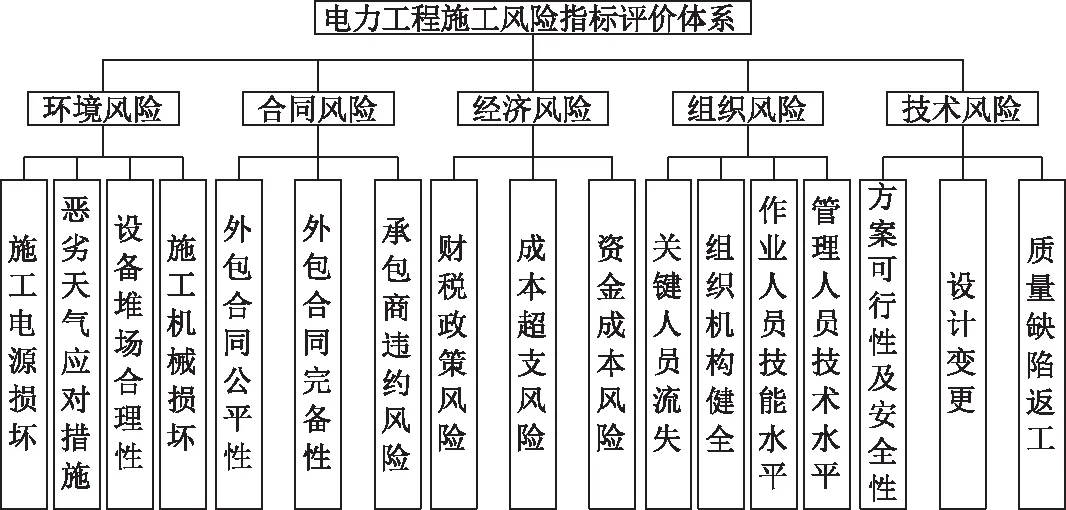
图1 电力工程施工风险评价指标体系

2 电力工程施工风险评价模型构建

2.1 确定因素集

风险评价的因素集表示为

一级因素集：U={U1，U2，U3，U4，U5}。

二级因素集：U1={u11，u12，u13，u14}；U2={u21，u22，u23}；U3={u31，u32，u33}；U4={u41，u42，u43,u44};U5={u51，u52，u53}。

2.2 确定评价集

将风险评价等级分为5个级别：很大、较大、一般、较小、很小，依次使用V1、V2、V3、V4、V5表示。用α表示风险水平系数，V1(很大)即α=1，表示存在非常大的风险；V2(较大)即α=0.75；V3(一般)即α=0.5；V4(较小)即α=0.25；V5(很小)即α=0，表示全部按计划进行，各方面进展呈理想状态，没有风险。工程实际中零风险是几乎没有的。

v={V1，V2，V3，V4，V5}

式中v是评价集，Vn(n=1，2，3，4，5)是各种可能出现的评判结果。

2.3 确定隶属度

通过电力工程施工行业的专家和经验丰富的技术人员对各评价指标的风险水平进行打分，汇总各指标属于很大、较大、一般、较小、很小中各个风险等级的专家数，并用各风险等级的专家数除以专家总数，作为评价因素uij对风险评价等级Vn的隶属度值rn(uij)。用矩阵A表示各指标的隶属度

其中rn(uij)为因素集中uij属于评价集中Vn(n=1，2，3，4，5)的隶属度。

2.4 确定权重集

采用反熵权-AHP法的组合权重法确定因素集中各评价因素的综合权重值。

2.4.1 AHP法主观赋权

运用AHP法确定指标主观权重。

(1)构造判断矩阵及一致性检验

对同一层次的各因素关于上一层中某一因素的重要性进行两两比较，构造判断矩阵

B=(bij)n×n

(1)

式中n为评价指标数量，bij满足：

bii=1，bij=1/bji，i,j=1，2、…，n。

构造判断矩阵进行两两比较判断时，由于客观事物的复杂性，我们的认识常常带有主观性和片面性，因此判断矩阵还必须进行一致性检验。一致性比例CR计算公式为

CR=C/R

(2)

式中C为一致性指标，C=(λmax-n)/(n-1)，λmax为判断矩阵A的最大特征值；R为随机一致性指标，其值可通过查表获得，它根据评价指标的数量n而变化。一致性比例CR<0.1时，判断矩阵A的一致性可以接受，否则应对判断矩阵进行相应修正使其满足一致性。

(2)确定指标层主观权重。

采用根法[11]和归一化方法计算指标层的主观权重

(3)

2.4.2 反熵权法客观赋权

对传统熵权法进行改进，形成一种反熵权法，克服了熵权法灵敏性高而容易使指标失效的缺点，使指标的不确定性程度得到有效改善，权重的波动性也得到相应减小[12]。定义一种反熵为

(4)

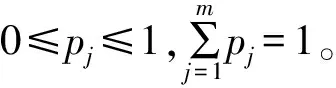
反熵的特征是指标的差异性与反熵值成正比关系，这与熵值恰恰相反。运用反熵权法进行客观赋权的步骤如下。

(1)标准化处理

采用Min-max标准化处理方法，最优值记为1，最劣值记为0，将m个方案中的同一项指标离散分布到0～1区间范围，充分体现各方案的差异性，并将逆指标转化为正指标[13]。

风险指标值越小越优，其标准化方法为

(5)

(2)计算反熵

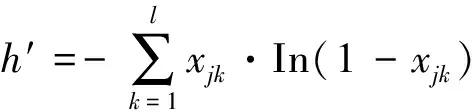
(6)

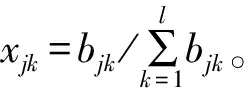
(3)确定权重

对计算出的反熵进行归一化处理，从而得到各指标的反熵权值[14]，即客观权重

(7)

2.4.3 反熵权-AHP法的综合权重计算

综合权重wi的计算公式为

(8)

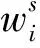
2.5 风险评价模糊关系的合成

记综合权重值W=(wi1，wi2…wim)，对评价指标进行综合评判，计算出评价向量D为

D=W×A

(9)

2.6 风险等级的确定

记模糊向量D=(di1，di2…dim)，根据最大隶属度原则，取风险评价得分E=max(di1，di2…dim),E所属风险等级即为电力工程施工风险评价的最终结果。

3 案例应用分析

内蒙古某电厂2×1000 MW发电工程#1锅炉为超超临界参数、变压运行直流炉，同步安装脱硫和SCR烟气脱硝装置，采用一层等离子、一层微油双层点火系统。安徽某电力工程公司负责#1锅炉安装工作，根据施工组织设计，资源环境配置上提供施工电源功率1100 kW，配备1台110 t塔吊、1台50 t塔吊作为主吊机械，布置2个设备堆场，特殊天气施工应急物资若干。管理人员组织机构由专业经理1名、生产经理1名、技术负责1名、技术员3名、质检员2名、安全员1名共计9名人员组成。根据施工部位及阶段将部分施工内容进行劳务分包，共划分为锅炉钢结构安装、锅炉本体安装、锅炉辅助机械安装、烟气脱硝装置安装、电除尘安装等共7个标段，签订分包合同7份。在技术管理方面共编制施工方案45份，施工图纸均由总承包方提供，工程进度款按月结算。

3.1 确定因素隶属度

由电力工程施工领域的资深专家和经验丰富的工程师，对该项目各级风险指标进行打分投票(有效问卷共回收20份)，以风险发生的可能性为投票标准，分别对每个单项指标进行评价，统计结果如表1。

根据各项指标的评价结果，进行归一化处理，得出评价指标的隶属矩阵为

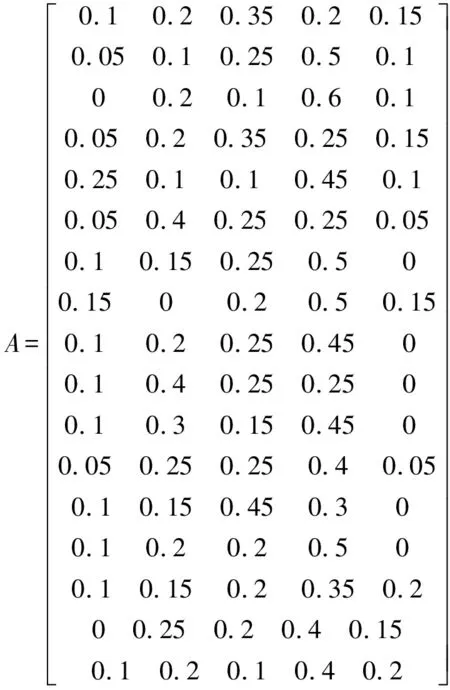
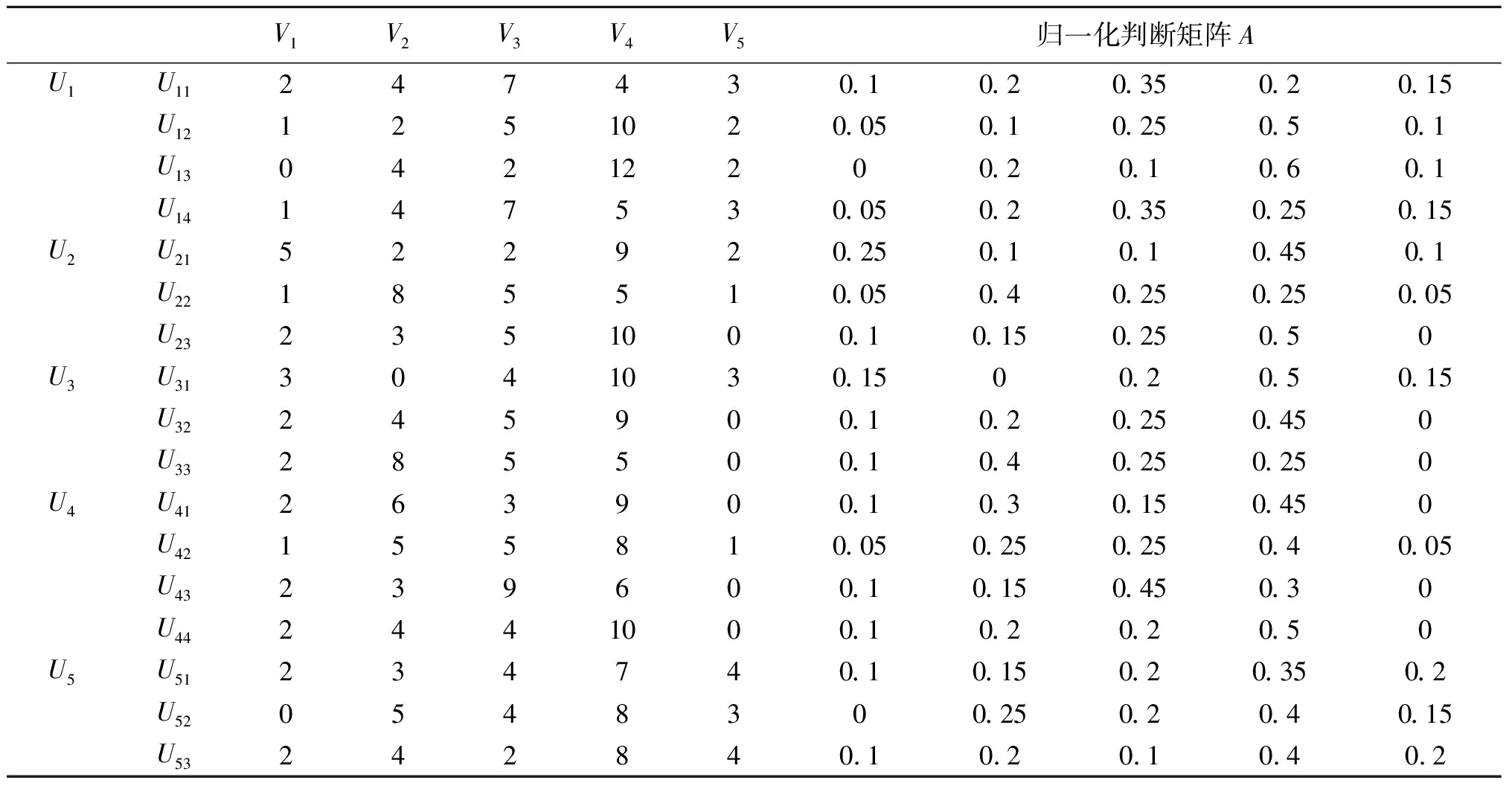
表1 各级指标投票结果及归一化判断矩阵

3.2 AHP法计算主观权重

计算总目标层权重，征求专家意见，得到判断矩阵，如表2。

表2 准则层各指标判断矩阵

最大特征根λmax=5.387。特征向量为W1=0.365，W2=0.083，W3=0.044，W4=0.177，W5=0.332。经检验，C=0.097，CR=C/R=0.097/1.12=0.086<0.1，判断矩阵具有满意的一致性。

计算分目标层权重，征求专家意见，得到判断矩阵，如表3。

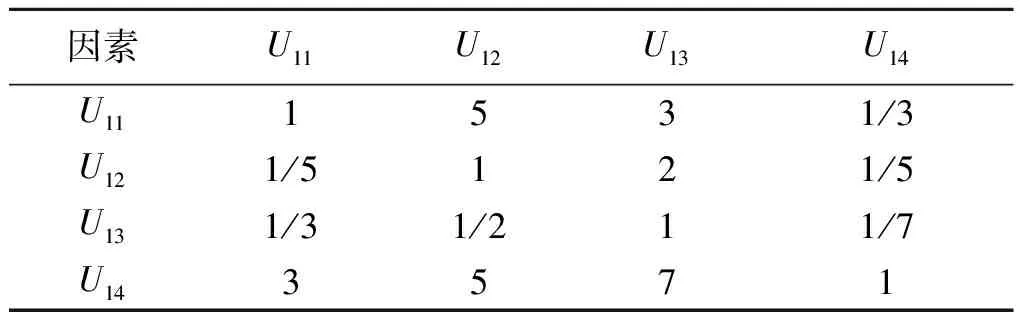
表3 分层次目标权重判断矩阵

最大特征根λmax=4.181。特征向量为W1=0.266，W2=0.095，W3=0.070，W4=0.569。经检验，C=0.060，CR=C/R=0.060/0.90=0.067<0.1，判断矩阵具有满意的一致性。

其他分层次目标权重计算过程同上，各层次的一致性检验结果均可以接受。根据以上计算，得出本项目风险因素集各指标的AHP权重，具体结果见表4。

3.3 反熵权法计算客观权重

根据电力工程施工阶段风险指标重要程度的投票结果，运用式(5)进行标准化处理，统计结果见表5。用式(6)和(7)得出相应的反熵权法权重向量，结果见表4。

3.4 反熵权-AHP法综合权重

运用反熵权-AHP法的组合权重计算公式(8)得出主客观综合权重W为

W=(0.088 0.036 0.025 0.173 0.015 0.082 0.010 0.005 0.009 0.025 0.017 0.017 0.082 0.048 0.163 0.045 0.158)

3.5 风险模糊关系的合成

通过式(9)可计算出模糊评价向量D。

D=(0.080.210.250.340.12)

3.6 风险等级的确定

根据最大隶属度原则，风险评价得分E=max(0.080.210.250.340.12)=0.34，所以工程的风险水平较小。虽然工程施工风险等级被评价为较小，但依然存在风险发生的可能性，需要进一步加强施工风险管理，针对性地采取必要措施，确保工程项目顺利进行。

3.7 评价结果分析

由表4可知，指标层U14的综合权重为0.173，U51的综合权重为0.163，U53的综合权重为0.158，U11的综合权重为0.088，U43的综合权重为0.082，U22的综合权重为0.082，以上6项因素的综合权重总和为0.746，占据很大比重，可视为该电力工程施工风险的关键因素，其中施工机械损坏U14权重达0.173，占比最大，影响程度也最大。

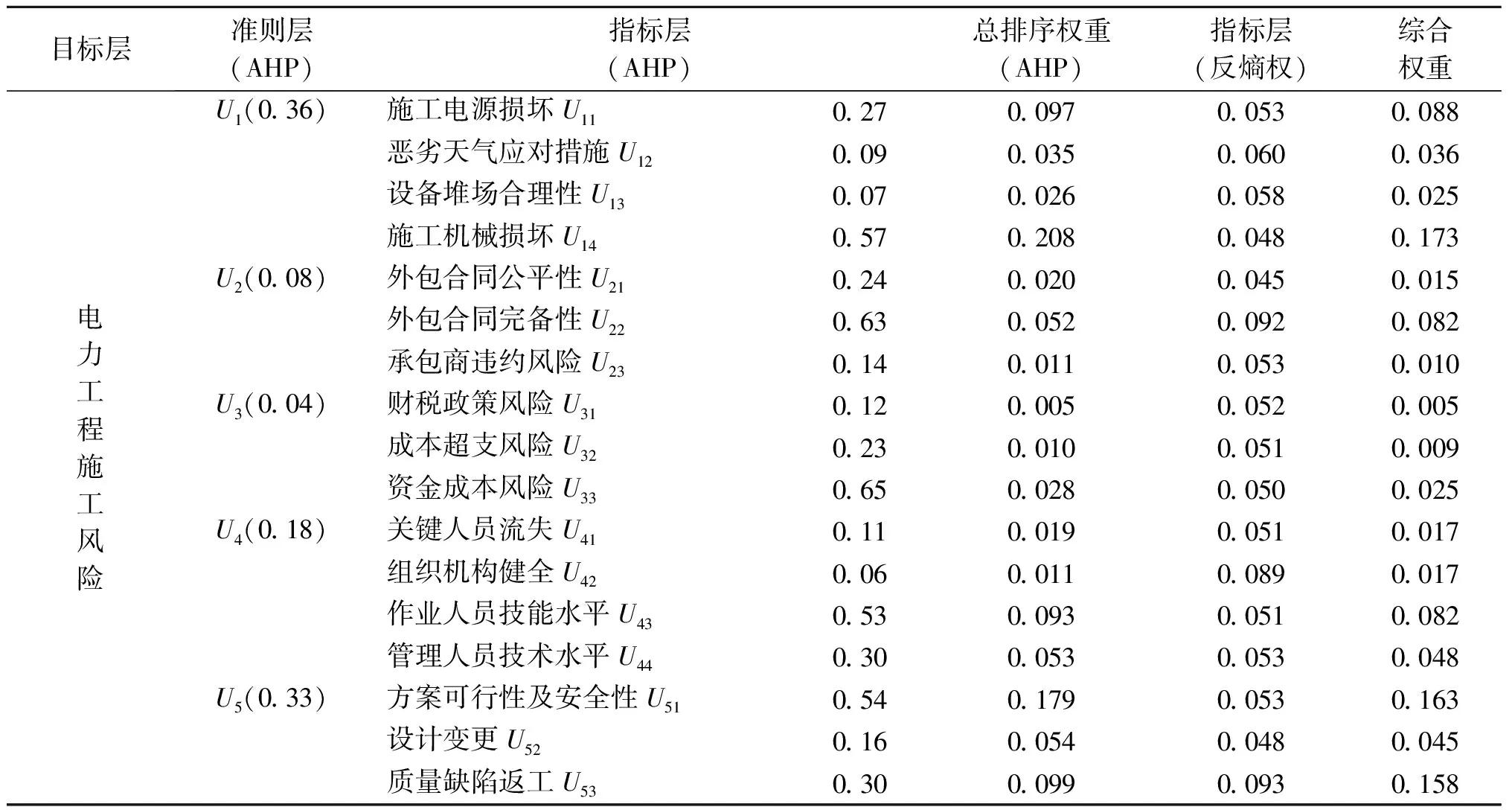
表4 风险因素集各指标的权重

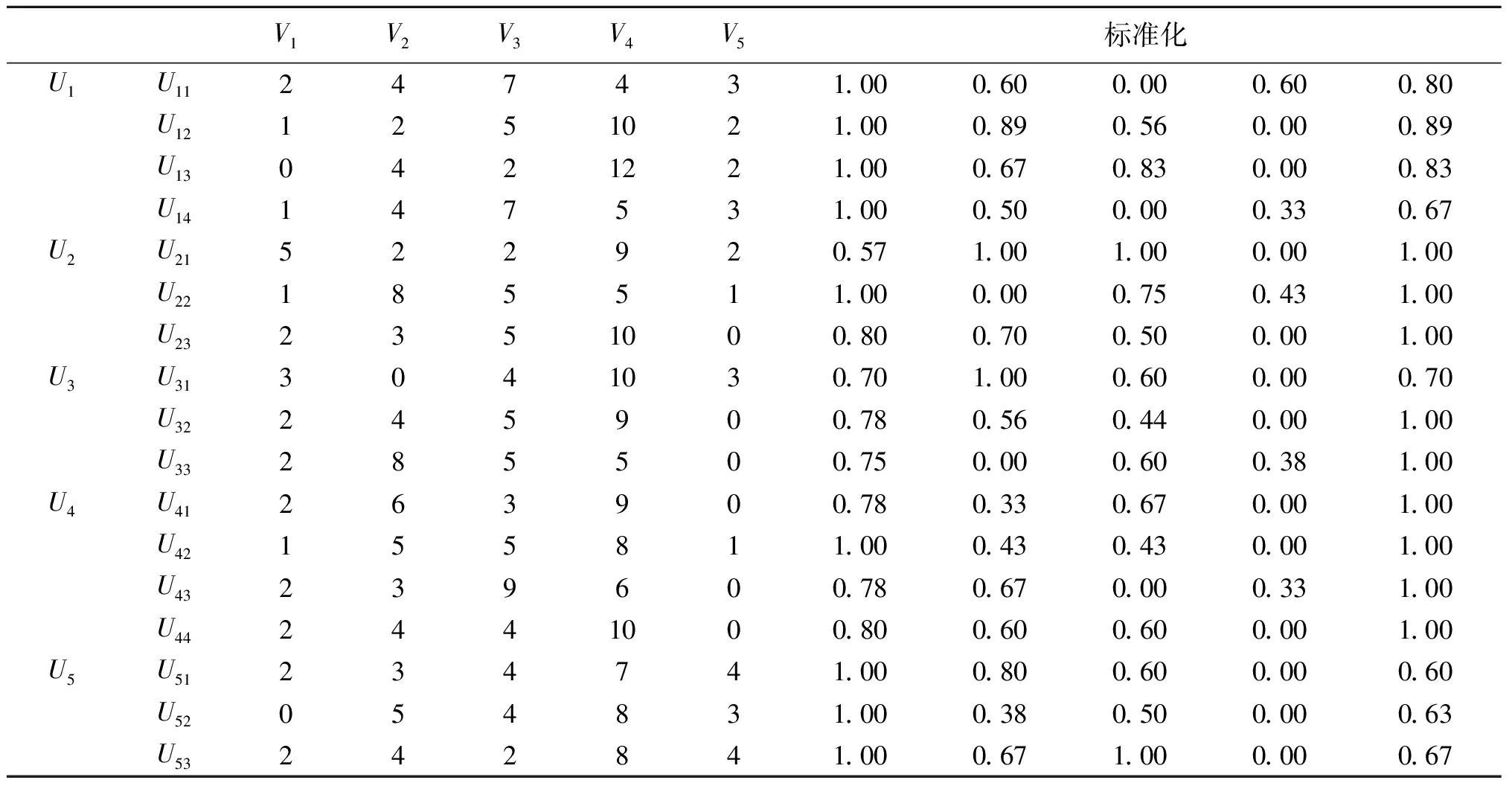
表5 各级指标投票结果及标准化矩阵

因此，在内蒙古某电厂2×1000MW发电工程#1锅炉施工过程中要高度重视施工机械损坏、方案可行性及安全性、质量缺陷返工、施工电源损坏、作业人员技能水平、外包合同的完备性这6项关键风险因素，加强对应的风险管理，积极采取风险应对措施，以降低工程施工风险。

该案例应用以目前电力工程中最先进的百万机组工程为视口，研究结论具有一定的代表性。

4 结语

本文构建了电力工程施工风险评价指标体系，综合考虑了影响电力工程施工风险的要素，融合得到环境风险、合同风险、经济风险、组织风险、技术风险5个方面的影响因素，并在此基础上，细分出17个二级评价指标因素，反映电力工程施工过程中所面临的风险状况。运用一种基于反熵权-AHP法的评价模型进行风险评价，将主观性较强的AHP和客观性较强的反熵权法结合确定综合权重，使评价结果更具有实际性和准确性。

分析了内蒙古某电力工程施工的风险状况，运用评价模型，计算风险评价得分为0.34，对应评价标准的较小，因此该工程施工的整体风险较小。对风险影响因素的综合权重进行分析，得到施工机械损坏、方案可行性及安全性、质量缺陷返工、施工电源损坏、作业人员技能水平、外包合同的完备性这6项关键风险因素，为施工单位积极采取风险防范措施提供了科学支撑。

使用反熵权-AHP法建立风险评价模型，将主观与客观方法结合起来评价电力工程施工风险，使得评价结果更加准确和科学，反熵权-AHP法适合用于对电力工程施工风险的评价研究并且具有自己独特的优势，丰富了电力工程施工风险评价方法，对于施工单位有效评价和防范风险具有指导意义。