基于Kalman 滤波的惯导系统重力扰动阻尼抑制方法*
朱九鹏,李 安,覃方君,李冬毅
(海军工程大学,武汉 430033)
0 引言
惯导系统作为全自主式的导航定位系统,可工作在空中、水面、水下等多种环境,并输出姿态、速度、位置等导航信息。但是由于传感器误差的存在,使得长航时工作的惯导系统的误差发散,进而影响导航的准确性。目前高精度的惯导系统的应用使得重力扰动的影响不能忽略。重力扰动包括垂线偏差和重力异常,重力异常在与姿态角误差耦合后形成的等效误差量级很小,仿真时通常忽略。而垂线偏差是实际重力在当地地理系下与正常重力的夹角,造成东向、北向均存在扰动分量,称为东向、北向重力扰动。目前为抑制重力扰动对惯导系统的影响,常采用重力补偿、阻尼抑制等方式。周潇等采用小波神经网络的方法进行重力扰动分量的补偿,速度、位置误差精度均有提升;杨功流等采用GPS 和惯导速度误差组合的方式进行Kalman滤波重力扰动估计从而实现补偿;翁海娜等采用传统固定系数的超前串联校正阻尼网络对重力扰动引起的误差进行抑制。对于长时间工作的水下载体,在未知外部信息的情况下,必须采用自主式的抑制方法。传统的阻尼网络参数需要经验调控,而且对于常值、随机性的重力扰动作用较小,一旦确定不可更改。本文提出利用Kalman 滤波的阻尼方法实现重力扰动误差的抑制,该方法可以自适应调整阻尼系数,仿真结果表明可以很快抑制舒拉振荡,同时位置、速度误差精度均有提升。
1 引入重力扰动的惯导误差模型建立
在以当地地理坐标系作为导航坐标系,未考虑重力扰动情况下采用正常重力γ进行解算,由于参考椭球面和大地水准面不完全重合的情况,不能直接使用正常重力直接解算,通常采用真实重力g,重力扰动δg的计算如下
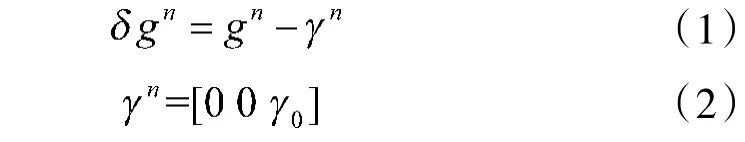
式中,γ通常由1980 大地参考系下得到,如式(3)
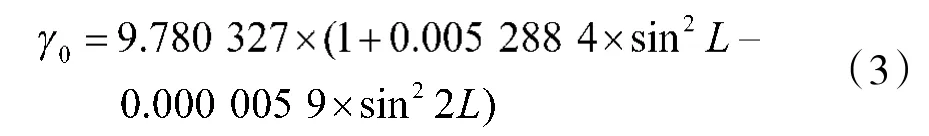
重力扰动的分量表达式如式(4)所示
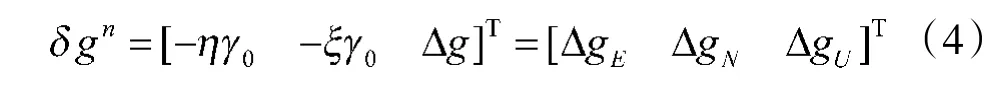
式中,η 和ξ 分别为垂线偏差的卯酉面分量和子午面分量;Δg、Δg、Δg分别为重力扰动的东向、北向、天向的分量。
由于舰船运动不考虑天向通道,因此,忽略天向重力扰动即重力异常的影响,只考虑水平方向的重力扰动对导航参数误差的影响。具体的姿态误差方程、速度误差方程、位置误差方程如式(5)所示。
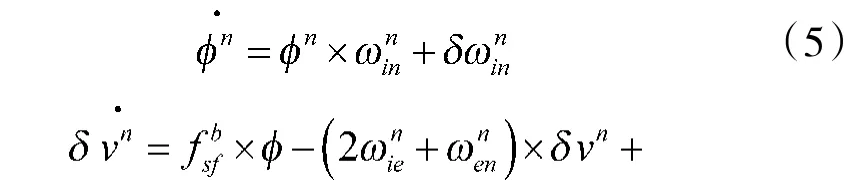

式中,ϕ 为东向、北向、天向姿态角误差;δv 为东向、北向速度误差;δp 为位置误差;w为地球自转角速度;δg 为东向、北向重力扰动;f为载体系下的加速度计输出的比力,此处假设卯酉圈半径和子午圈半径相等。
从上述的式子能够看出,水平重力扰动对导航参数的影响等效于加速度计误差,实际上是重力扰动在导航系下的投影影响了加速度计的测量值,进而影响了速度误差、位置误差,并与姿态角误差进行耦合。为观察水平重力扰动带来的误差,必须先获得重力扰动的大小,这里利用2190 阶的EIGEN-6C4 模型获取全球各地的水平重力扰动信息。当陀螺仪、加速度计精度达到一定量级时,在长时间航行状态的惯导中,重力扰动带来的影响不可被忽略。下面给出不同程度重力扰动对惯导速度、位置误差的影响。
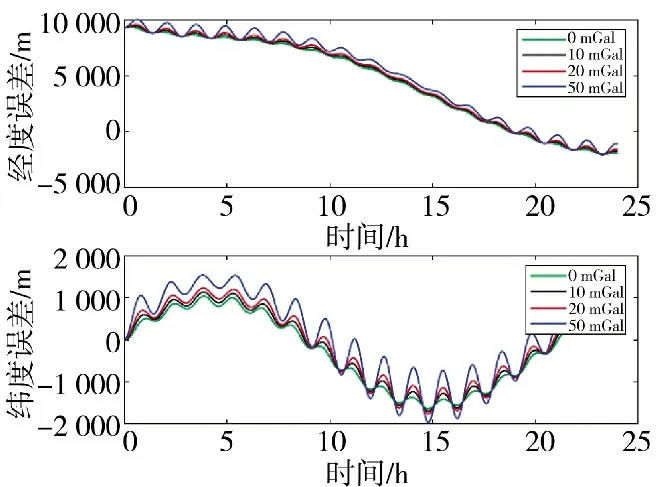
图2 不同重力扰动对位置误差影响
2 基于传统阻尼网络的重力扰动抑制方法
通过上一章的分析可知,重力扰动会使得惯导系统产生振荡性误差,尤其对于长航时的惯导系统,长时间的误差积累会严重影响导航的准确性,因此,对振荡性误差必须抑制。阻尼技术作为一种有效的手段经常被用来抑制周期性、振荡性误差。
根据传统阻尼方法对东向水平修正回路分析,得到姿态、速度、位置误差的传递函数如下
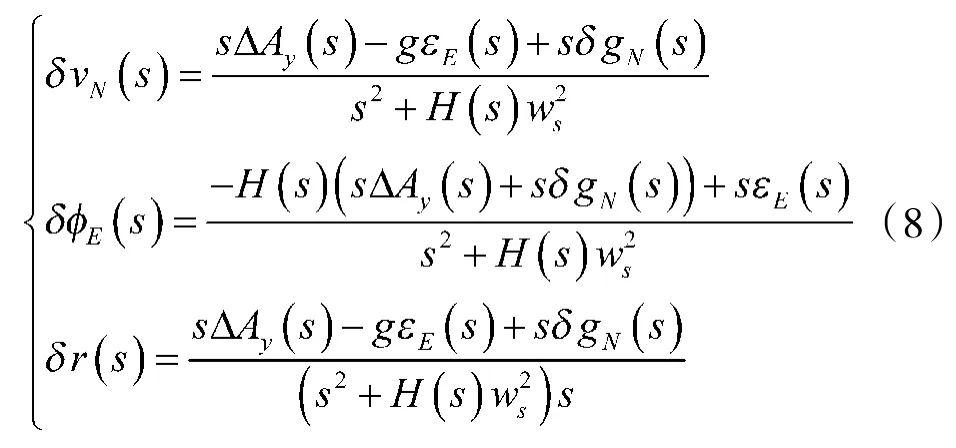
式中,ΔA为北向加速度计误差;ε为东向陀螺漂移;δg为北向重力扰动;w为舒拉角频率。
目前抑制重力扰动的阻尼网络的选取一般为超前串联校正网络,采取的形式如式(9)所示,其中,ξ 为阻尼系数。

水平阻尼网络抑制的是舒拉振荡分量和傅科周期分量,但是地球周期振荡则需要由方位阻尼进行抑制。这种由水平阻尼和方位阻尼构成的形式称为内全阻尼工作模式。目前采用的方位阻尼系数一般为0.5 左右,阻尼网络的各项参数则通过试凑法得到,常采用的方位阻尼网络如式(10)所示。
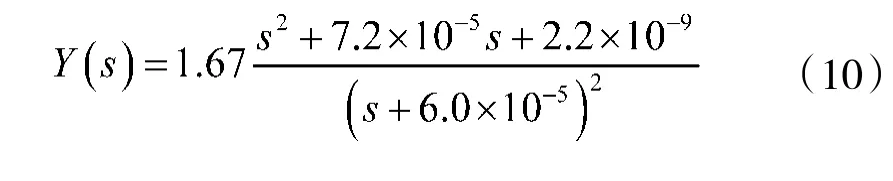
3 基于Kalman 滤波阻尼的重力扰动抑制方法
从上一章传统阻尼网络形式可知,阻尼的存在使得3 种振荡性分量均得到抑制,并且阻尼系数越大,振荡性误差的收敛速度越快。但是从其结构能够看出,传统阻尼网络的参数确定之后难以更改,控制参数需要根据经验得到,不具有自适应性。同时,舰船在长航时状态下,重力扰动并非定值而是呈现非规律性、随机性的变化,固定的阻尼系数针对常值重力扰动的误差抑制具有一定作用,但是在变化的重力扰动下,效果并不明显。因此,必须对不同程度的重力扰动进行不同程度的阻尼,以抑制重力扰动所导致的舒拉振荡性的误差,即采用变阻尼的方法实现不同程度的重力扰动抑制。本文采用一种基于Kalman 滤波阻尼的重力扰动抑制方法,反馈参数由Kalman 直接得到,并不需要反复调试。Kalman 滤波器是基于均方误差最小原理,使得输出的反馈系数具有最优性,同时减小误差的稳态值。
首先以东向水平修正回路为例,在如图4 所示的回路中可以得到临界稳定的东向回路,如式(11)
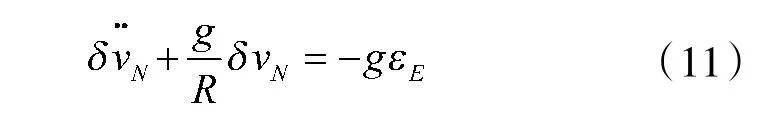
为实现系统的稳定,将系统的极点全部配置到左半平面内,因此,引入输出反馈的方式,引入输出反馈的东向回路的原理图如图3 所示,图中,k、k为反馈回路的比例系数,δv为外部传感器参考速度误差。
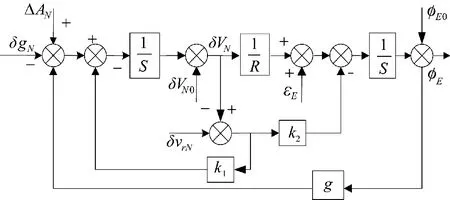
图3 引入输入反馈的东向水平修正回路
引入输入反馈后,东向回路的速度、姿态误差的微分方程则改变为式(12)
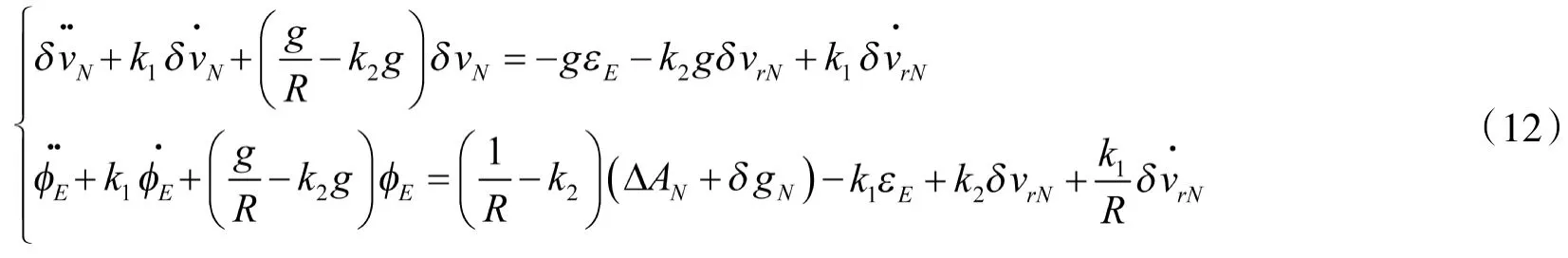
通过对上式方程分析,速度、姿态误差的微分方程均为二阶方程进行拉普拉斯变换后同为二次多项式,即误差传递函数为二阶系统。要想使系统由临界稳定变成稳定,则必须保证极点全部位于左半平面,即二阶系统分母根均小于0。根据分析,若要求根均小于0,则必保证反馈系数k>0,k<0。根据自动控制理论,该二阶系统的等效阻尼比ξ 以及无阻尼自振荡频率w满足式(13)
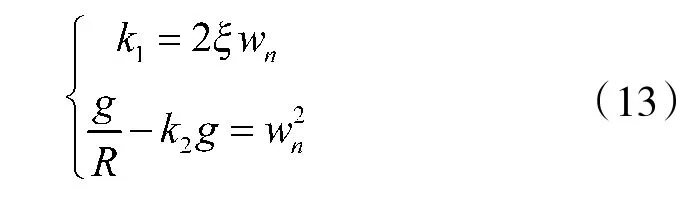
通过对东向水平回路引入输入反馈系数实现阻尼比的自适应调节,初始时具有较大的阻尼比使振荡误差快速收敛,振荡误差基本消失时,阻尼比同样收敛。为实现k、k的自适应调节,从而减小速度、姿态误差,因此,引入Kalman 滤波器实现求得使得误差最小的滤波增益矩阵,从而得到反馈回路的控制参数。
舰船在运动时重力扰动才会呈现出非规律性的变化,因此,需要考虑惯导在动基座的情况下的误差方程,将式(5)~式(7)以及引入输入反馈后,变换成矩阵形式如下式

其中,

假定某线性系统结构如下
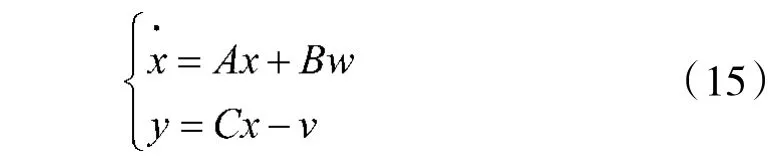
则根据Kalman 滤波器原理可得估计误差的方程为式(16)
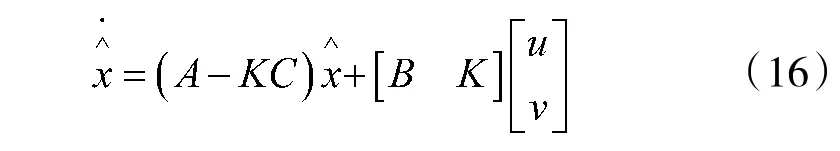
引入外速度误差下的Kalman 滤波器以参考速度误差作为观测量,因此,有
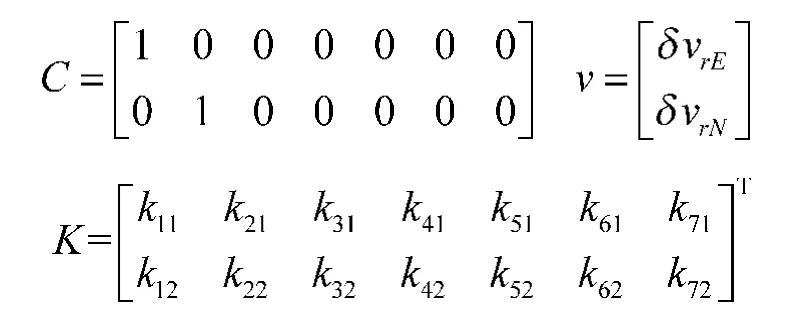
对比式(15)和式(17)则可以得到
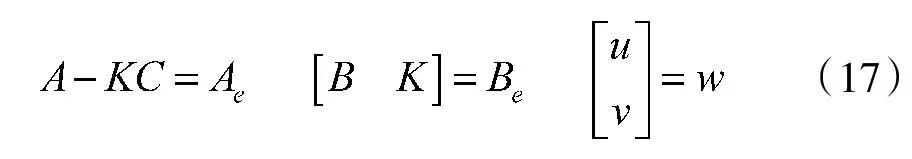
当式(16)代表的系统满足式(18)时,可将动基座下的惯导误差量x视为Kalman 滤波器的估计误差进行处理,由滤波器求得的增益矩阵K 满足均方误差最小的性质,此时K 中的每一行元素代表每个反馈回路的比例系数。由于只需要求解增益矩阵即可,因此,采用简化后的Kalman 滤波方程,如式(18)所示
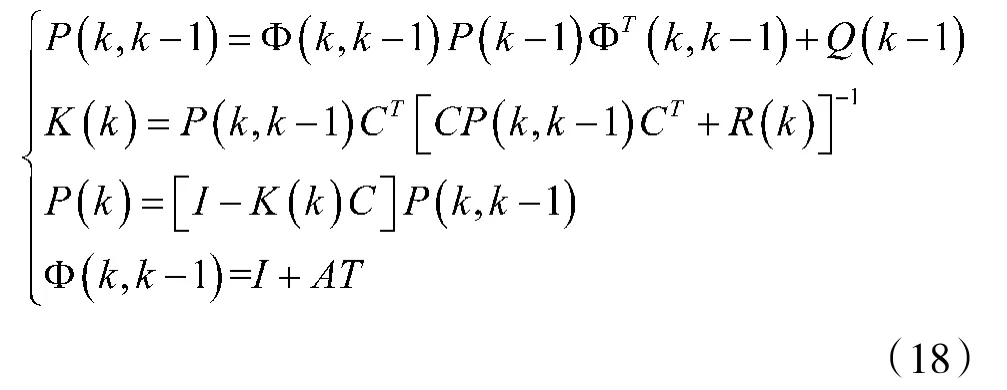
式(18)为离散化处理后的Kalman 滤波器方程,T 为滤波周期;P(k,k-1)为一步预测方差阵;P(k)为状态估计均方误差阵;R(k)为量测噪声方差阵,由DVL 测得的外速度误差的方差决定;Q(k)为过程噪声方差阵,由陀螺和加速度计以及水平重力扰动的噪声方差决定。
通过对系数矩阵A 的分析可知,纬度误差几乎始终贯穿其他误差,相对其他误差影响较大,因此,在考虑动基座情况下不对纬度误差回路进行输入反馈,即使k=k=0。
4 仿真验证
根据对图1 的阻尼回路,使惯导工作在内全阻尼的模式下,对于式(10)所示的阻尼网络取ξ=0.5;针对惯导常见误差值进行阻尼方法的验证,加速度计常值零偏取ΔA=9.78em/s,ΔA=9.78em/s;加速度随机零偏取ΔA=9.78em/s;陀螺常值漂移取ε=0.003°/h,ε=0.003°/h,ε=0.003°/h;陀螺随机漂移取ε=0.000 2°/h;初始速度误差为δv=0.05 m/s,δv=0.05 m/s;初 始 失 准 角 分 别 为:ϕ=3',ϕ=3',ϕ=5';舰船东向、北向航速v=0 m/s,v=3 m/s;舰船初始位置为20°N,203°E,舰船航行总时间为24 h,仿真步长0.1 s,为反映重力扰动变化,下面给出舰船运动的航迹上水平重力扰动的变化趋势,仿真所用重力扰动数据分辨率1'×1',仿真结果如图4 所示。

图1 不同重力扰动对速度误差影响
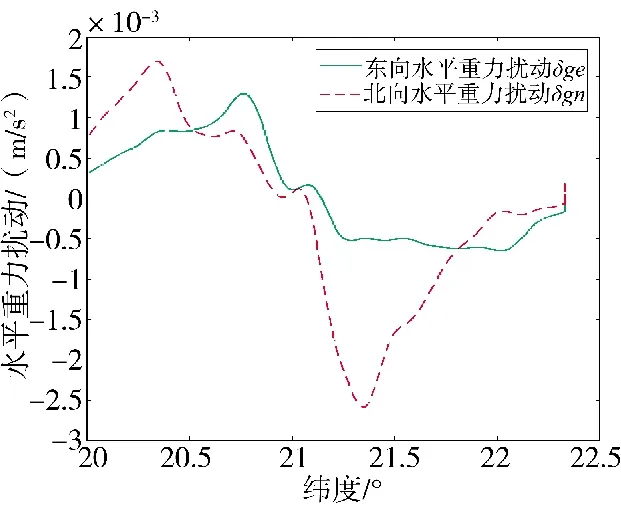
图4 水平重力扰动曲线变化图
对Kalman 滤波器初始值进行设计,均方误差阵为初始各导航参数误差P=diag(0.05 m/s 0.05 m/s 0.001 rad 0.001 rad 3' 3' 5'),过程噪声阵的设置按照上面Q=diag(1 μg 1 μg 0 0 0.003°/h 0.003°/h 0.003°/h),R 为DVL 的噪声方差,这里为量测噪声方差R=diag(0.005 m/s 0.005 m/s),滤波周期T=1 s。采用本文方法效果和超前串联校正阻尼网络方法如图5~图11 所示。
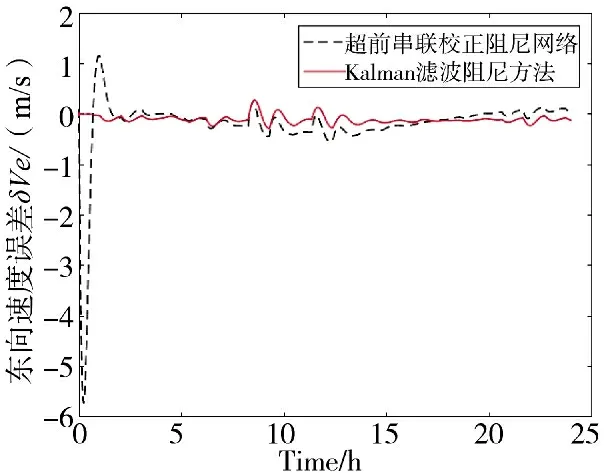
图5 东向速度误差结果对比图
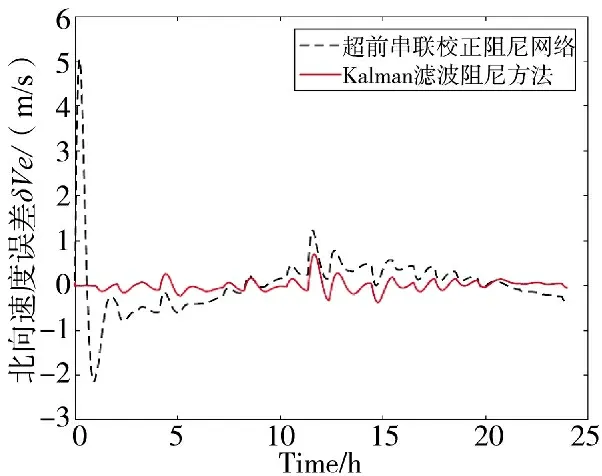
图6 北向速度误差结果对比图
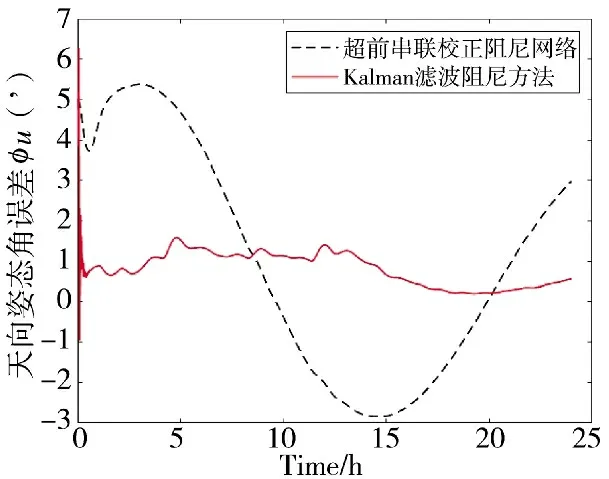
图11 天向姿态角误差结果对比图
1)通过对表1 中速度误差的分析,很明显舒拉振荡和傅科振荡都被很好地抑制,初始2 h 内东向、北向速度误差较大的超调量,而后不断减小直至收敛;而Kalman 滤波阻尼方法则能够使振荡误差收敛加快,效果完全优于超前串联校正阻尼网络;后期振荡误差收敛之后,由于水平重力扰动误差量级大于高精度惯导系统惯性器件误差,且非规律变化,因此,两者变化趋势都呈现出波动状,但是Kalman 滤波阻尼方法能够使速度误差几乎保持在0 m/s 附近,而超前串联校正阻尼网络则呈现出较大的波动,经过阻尼后Kalman 滤波阻尼方法能够使速度误差降低约0.8 m/s。
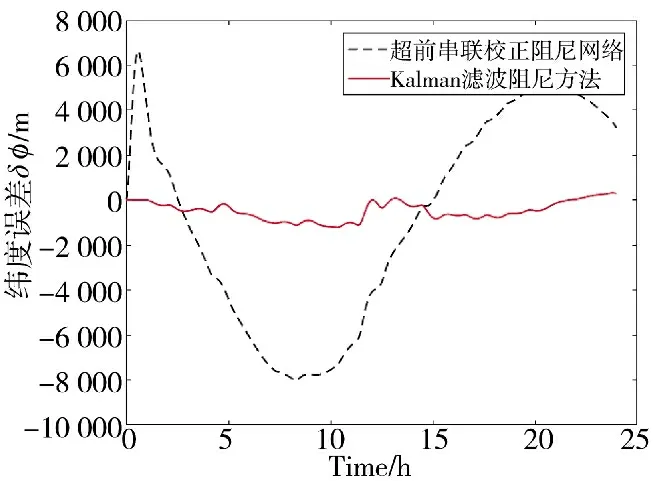
图7 纬度误差结果对比图
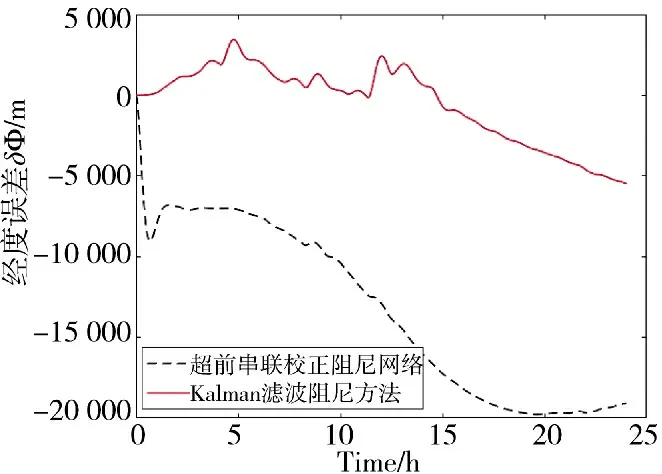
图8 经度误差结果对比图
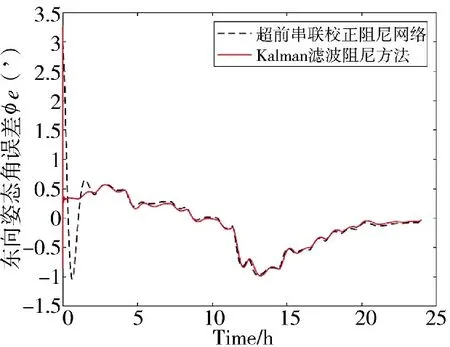
图9 东向姿态角误差结果对比图
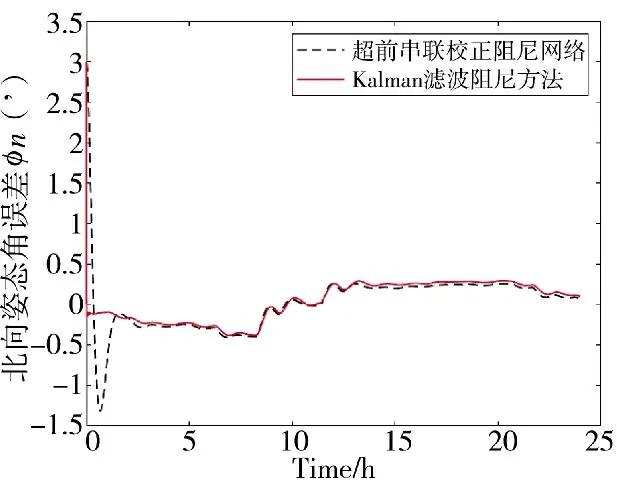
图10 北向姿态角误差结果对比图
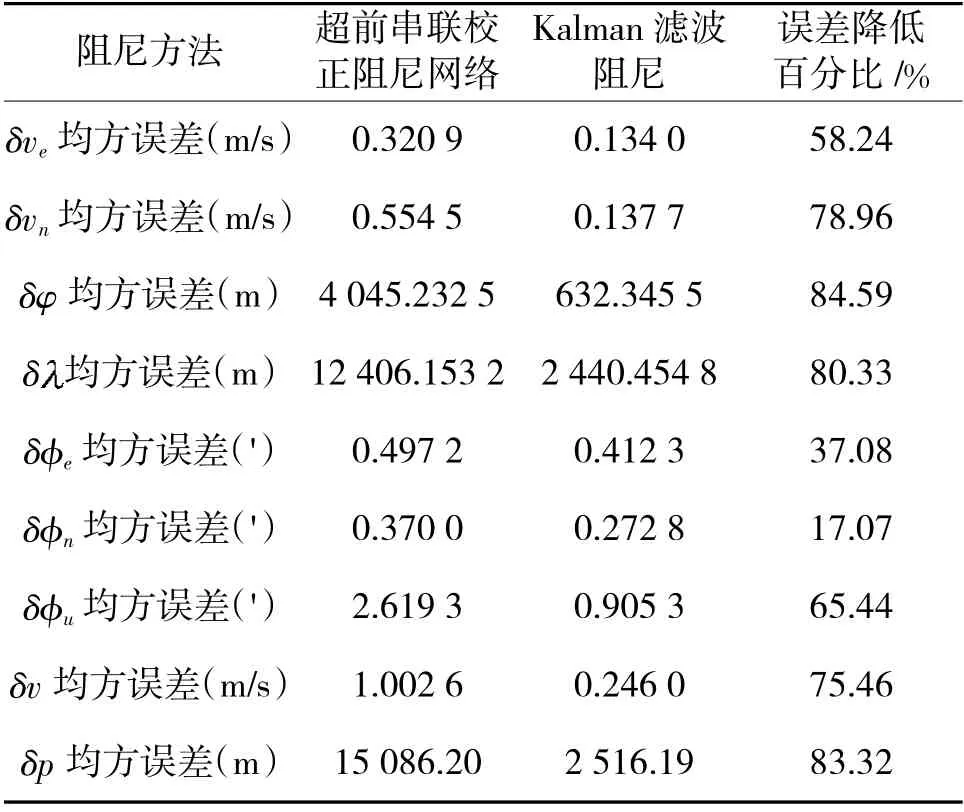
表1 导航参数误差均方值(RMSE)及误差降低百分比
2)对于位置误差,同样地振荡性误差均被抑制,但是纬度误差整体呈现出较大的波动,说明超前串联校正阻尼网络的地球周期在一个周期内没有被完全抑制,且最大的纬度误差可达6 000 m,而Kalman 滤波阻尼方法最大1 000 m,且一个地球周期内就被完全地抑制,纬度误差降低约3 000 m;经度误差依旧呈发散趋势,但是从两种方法的比较来看,Kalman 滤波阻尼方法明显优于超前串联校正阻尼网络,两者之间的差距较大;从上述纬度误差和经度误差来看,Kalman 滤波阻尼方法能够非常有效地降低位置误差,并且减弱经度误差的发散趋势。
3)对于姿态误差角的变化,东向和北向的误差角最后收敛的趋势比较一致,均方误差变化不大,差异主要在前期抑制振荡性误差的速度,Kalman 滤波阻尼方法比超前串联校正阻尼网络要快近2 h。天向误差角的抑制效果要明显一些,Kalam 滤波阻尼方法降低约1.7'。
5 结论
随着惯性器件的制作工艺提高,加速度计和陀螺仪的精度也随之提升,高精度惯导系统在航海领域应用越来越广泛,重力扰动的数量级相比于加速度计零偏也变得不可忽略,甚至超过了惯性器件误差的固有影响。因此,必须对其进行抑制或者补偿,对于未知重力扰动信息或者难以获得重力信息的情况下,阻尼抑制方法作为一种手段非常有效。本文首先建立了考虑重力扰动的惯导误差模型,分析了重力扰动对导航参数误差的影响。针对超前相位串联阻尼网络不适用于随机性、非规律性的水平重力扰动,采用基于Kalman 的变阻尼技术,通过引入反馈回路,改变系统稳定性,再根据Kalman 滤波器的原理,求解反馈回路的控制系数,实现等效阻尼比的自适应性变化。通过仿真进行验证该方法的有效性,仿真结果表明,基于Kalman 滤波的阻尼方法除了可以快速、有效抑制振荡性误差,还可以有效地降低重力扰动带来的速度、位置误差。24 h 的仿真结果表明,速度误差能减小约0.8 m/s,降低75.46%,位置误差减小约12 000 m,降低83.32%,天向误差减小约1.7',降低约65%。

