基于LADRC 技术的光伏MPPT 控制策略研究*

陈 荣张林

(1.盐城工学院电气学院，江苏 盐城 224051；2.江苏大学电气信息工程学院，江苏 镇江 212013)

光伏发电以其环保、易安装等特点成为新能源发电领域研究热点[1]。光伏阵列产生的电能经过DC/DC 变换器后再逆变馈入电网，在电能转换的过程中，由于控制方法、器件损耗、外部干扰等原因，电能转换效率并不能达到100%，其中器件损耗可以从器件选型上进行改善，如选择导通电阻小的MOSFET、二极管和ESR 较低的电解电容等。对于由控制方法的不同和来自外部干扰信号而造成的功率损耗，则可以通过改进控制方法来降低[2-3]。当温度和光照强度等因素保持不变时，光伏系统输出功率存在唯一极值点，这个极值点即系统的最大功率点，当外界环境因素发生变化时，光伏系统的极值点将发生偏移，系统实际最大功率点改变。因此，跟踪变化的最大功率点是减小系统功率损耗的有效方法，MPPT 控制器的设计是决定跟踪精度的关键环节[4]。

PID 控制器在控制领域中占据着绝对主导地位，其优点有:(1)在保持电路参数不变的条件下，不需要知道被控对象的具体模型，根据输出反馈量和输入给定量之间的误差控制从而达到稳定系统的目的；(2)只需要调整kp、ki和kd这3 个参数，参数整定方便[5]。但是PID 的缺陷比较明显，文献[6-8]详细分析有:(1)直接根据给定量和输出反馈量计算误差的方法不合理，当给定量跳变时，与不能跳变的输出反馈量作差会得到跳变的误差；(2)使用传统的线性微分器提取误差的方法不能充分发挥其反馈作用；(3)比例、积分、微分的线性组合不一定是最好的；(4)积分反馈的弊端:造成闭环系统响应变慢、输出功率振荡。因此，为了在保留PID 控制器优点的同时弥补其缺陷，韩京清提出了自抗扰控制(Active Disturbance Rejection Control，ADRC)技术，由跟踪微分器(Tracking Differentiator，TD)、扩张状态观测器(Extended State Observer，ESO)以及非线性状态误差反馈(Nonlinear State Error Feedback，NLSEF)控制律组成，针对PID 控制器的缺陷做了如下改进:(1)事先安排过渡过程，扩大了误差微分反馈增益的选取范围和对象参数范围，增强了控制器的鲁棒性；(2)改变微分信号提取方式，由TD 和ESO 输出信号作差提取微分；(3)采用非线性组合，具有良好的适应性和快速收敛的特性；(4)采用ESO 并取消积分反馈，预估扰动并提前给出补偿[9-11]。由于非线性ADRC 需要整定的参数过多，调参相对比较复杂，故高志强提出线性ADRC(Linear ADRC，LADRC)，将需要调整的参数减少到3 个，效果与非线性ADRC 接近，极大地降低了参数整定的难度，促进了 ADRC 技术的推广与应用[12-15]。

为了让光伏系统在受到干扰时仍然具有良好的鲁棒性和稳态精度，本文设计了一种基于LADRC技术的MPPT 控制器，并将其应用到直流母线电压Uo的电压反馈环路中，替换原电压环路中的PID 控制器。搭建LADRC 仿真模型，并对提出的基于LADRC 技术的光伏系统前级Boost 电路进行仿真验证，分别改变温度和光照强度得到多组输出功率波形，与基于PID 控制器的光伏系统前级Boost 电路输出功率形成对照，基于LADRC 控制器的光伏系统前级Boost 电路在受到干扰时仍然具有较快的动态响应速度和良好的稳态精度，而基于PID 控制器的光伏系统前级Boost 电路在干扰下动态响应速度快，但是有较大的功率振荡和功率损耗，仿真实验证明了该方法可以给光伏系统带来更强的抗干扰能力和更高的稳态精度。

1 光伏电池与光伏系统建模

1.1 光伏电池数学模型

搭建光伏电池等效模型如图1 所示，其中Iph是光生电流，Ipv和Upv分别为光伏电池的输出电流与输出电压，I0为二极管反向饱和电流，Rs和Rsh分别为光伏电池的串联电阻和并联电阻，表示光伏电池的损耗，q为电荷常量，A为二极管的理想系数，K为玻尔兹曼常数，T为光伏电池板所处的环境温度[16]。

图1 光伏电池等效电路

根据此等效电路，由基尔霍夫定律得:

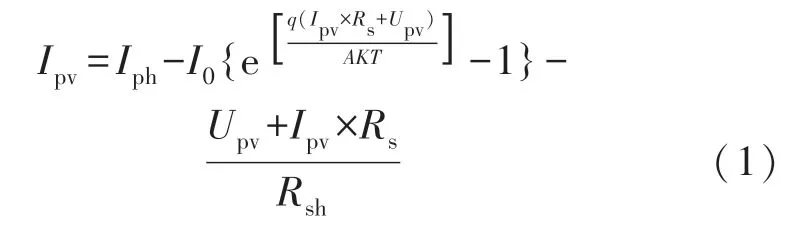
式中:Rsh的值一般很大，且有Rsh远大于Rs，故式(1)的第三项(Upv+Ipv×Rs)/Rsh近似为零，则上式简化为:

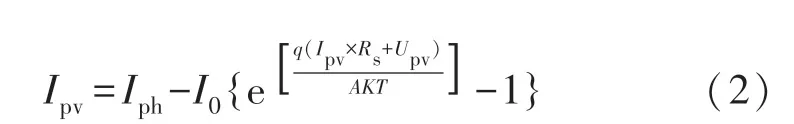
设I0=C1Isc，AKT=qC2Uoc，当环境因素以及电池参数不变时可以认为C1和C2为常数，代入式(2)可得:

用S表示光照强度，那么在标况下(标况是指温度Tref=25 ℃，光照强度Sref=1 000 W/m2)可以得出C1和C2:

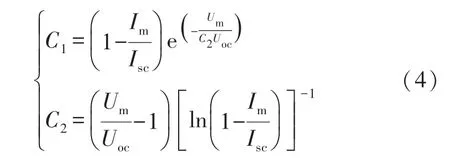
式中:光伏电池输出端开路电压Uoc、短路电流Isc、最大功率点电压Um、最大功率点电流Im。

定义温度的变化量ΔT和光照强度的相对变化量ΔS:

在实际情况下，温度和光照强度的变化都属于光伏系统的外部扰动，因此当产生外部扰动时，需要重新计算参数值，干扰下的参数值计算如下:

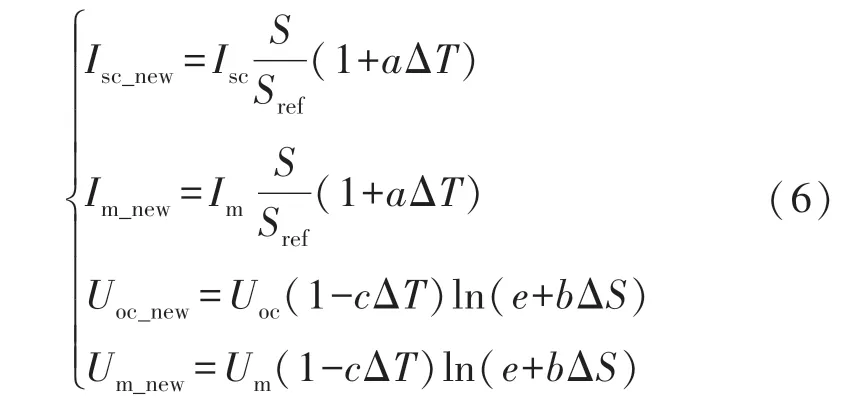
式中:常数a，b，c的典型取值为a=0.002 5，b=0.5，c=0.002 88。

根据式(3)～式(6)可以在MATLAB/Simulink中搭建光伏电池的仿真模型，分别改变T和S，得到光伏电池输出功率曲线如图2(a)和图2(b)所示。横坐标U表示端口电压，纵坐标P表示输出功率。

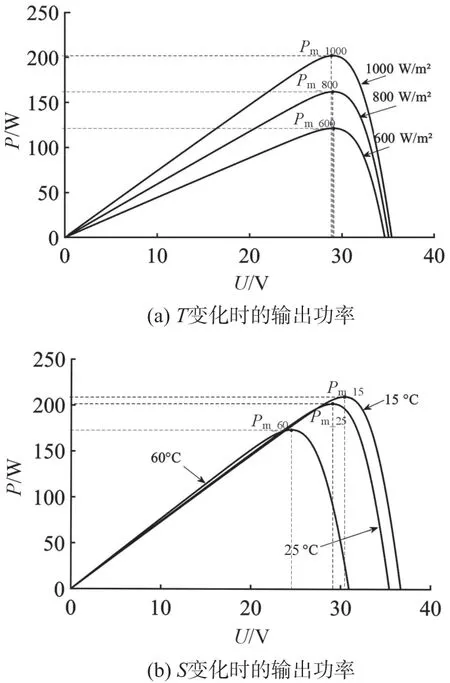
图2 T 和S 变化时的输出功率

由图2 可知，当外部扰动对光伏系统产生干扰时，光伏系统的输出功率会发生变化，具体为:T增加，输出功率减小，反之输出功率增大；S增加，输出功率增大，反之输出功率减小。以标况下的功率曲线为参照曲线，记录每条曲线的最大值点坐标，得到的最大功率点功率和最大功率点电压之间的关系如表1 所示。

表1 不同环境下的最大功率与电压之间的关系

1.2 光伏系统DC/DC 电路模型

光伏系统包括前级DC/DC 电路和后级DC/AC电路，前级多采用Boost 升压电路，图3 为光伏系统Boost 电路模型。

图3 光伏系统Boost 电路模型

设变换器输入阻抗为Zin，输出阻抗为Zout，开关管VT 的占空比为D，改变Boost 变换器开关管VT 的占空比D可以改变输入阻抗和输出阻抗之比，当输入阻抗和输出阻抗匹配时直流侧输出功率最大。在不考虑外部干扰和内部干扰情况下，由状态空间平均法可以列出系统状态方程:

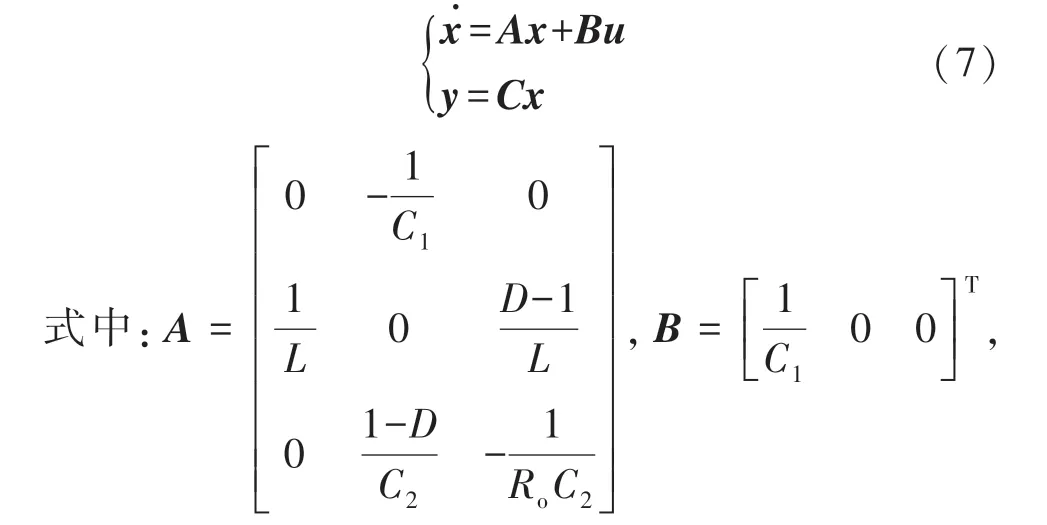
C=[0 0 1]，x=[UpvILUo]T，u=Ipv，D为变换器占空比，y为输出量Uo。

1.3 光伏系统建模

搭建光伏系统仿真模型，并将相应子模块封装，如图4 所示，PID 控制器模块可以替换成LADRC 控制器模块，MPPT 控制算法采用双模式功率预测温度补偿扰动观察法，输出参考电压Vref经PID 控制器后，再经过PWM 模块产生控制Boost 变换器开关管通断的控制信号，用Signal Builder 模块模拟随时间变化的光照强度和温度。

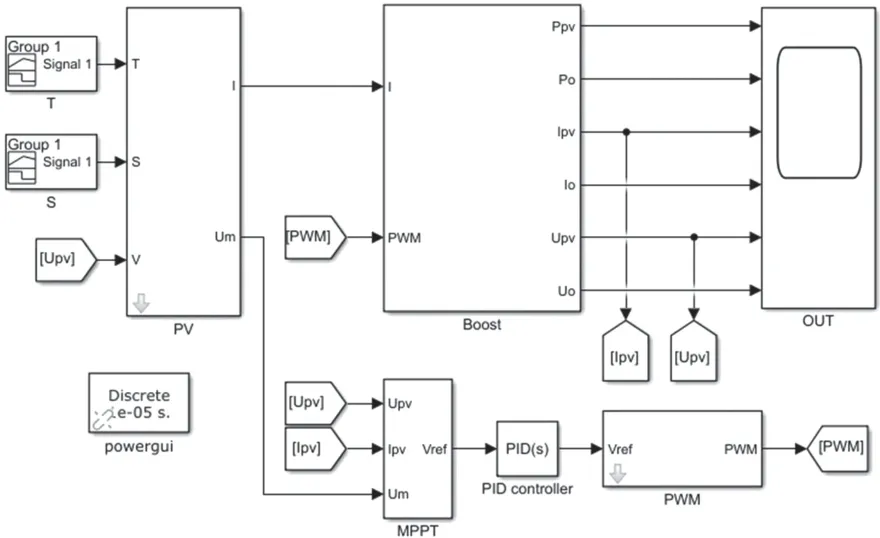
图4 光伏系统仿真模型

2 基于LADRC 的MPPT 控制器设计

2.1 MPPT 控制器设计

由于非线性ADRC 控制器设计难度较大且参数整定更复杂，故选择一阶LADRC 控制器，省略TD，简化NLSEF 并用比例控制代替。提出基于直流母线电压Uo构造线性自抗扰控制器，并推导其小信号模型，假设光伏系统受到干扰，则在各稳态量上加入扰动量可得:

式中:“-”表示其中的平均分量，“＾”表示其中的脉动分量，“·”表示该变量的微分。

式(8)等式左边为瞬时值，右边为稳态值与扰动值之和，引起扰动的因素可以是光照强度、温度、开关损耗等。直流侧母线电压为Uo，由式(7)可得:

将式(8)代入式(9)可得:

式中:D′=1-D，光伏系统外部干扰为w，则加入外部干扰后式(11)可以写为:

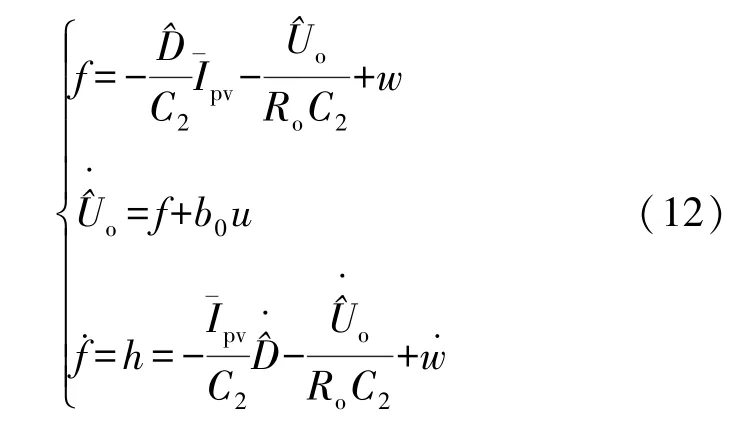
式中:f为内部扰动和外部扰动之和，扰动因子b0=D′/C2，输入量u=根据上述系统设计一阶LADRC，令x1=?x2=f，则二阶线性ESO(Linear ESO，LESO)可以写为:

式中:输出量y即为直流侧电压Uo，β1和β1为误差增益，将LESO 极点配置在-ω0处，则:

设计比例控制器为:

式中:kp为比例系数，Vref为MPPT 控制器输出的参考电压，将极点配置在-ωc处，可得:

求解式(16)可得:kp=ωc，ωc为控制器带宽。

生成控制对象输入量:

式中:b0为扰动因子。

综上，可以得出光伏系统的控制框图如图5所示。

图5 光伏系统控制框图

2.2 基于LADRC 控制器的光伏系统仿真搭建

根据式(13)、式(15)和式(17)搭建LADRC 控制器的仿真模型，简化后的LADRC 控制器由LESO模块、比例控制模块和控制律模块组成，如图6 所示，左侧为LESO 模块，中间为比例控制器模块，右侧为控制律模块，需要整定的参数为ω0、ωc和b0，将其封装成一个子模块，并命名为LADRC。

图6 LADRC 控制器子模块结构

对搭建的LADRC 控制器模块进行仿真验证，测试其抗干扰性能，如图7 所示，其中输入量v为单位阶跃信号，u为LADRC 控制器输出量，控制对象的传递函数设置为10/4s+1，y为控制对象的输出量。假设系统未受任何干扰时，将图7 中LADRC 控制器换成PID 控制器作为对照组，与图7 中采用LADRC 控制器的系统抗干扰能力进行对比，在1 s时刻加入单位阶跃信号模拟外部干扰。

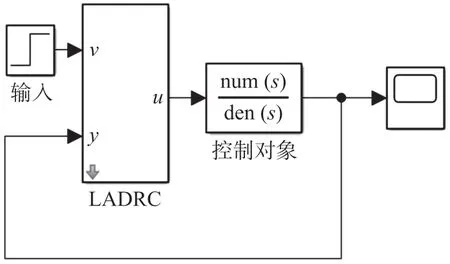
图7 LADRC 控制器仿真验证

LADRC 控制器和PID 控制器的仿真参数如表2所示，其余参数不变。两种控制器仿真对比结果如图8 所示。

表2 LADRC 和PID 的仿真参数

仿真得到一组LADRC 控制器和PID 控制器的结果对照，曲线a为输入阶跃信号，曲线b为采用PID 控制器的系统输出，曲线c为采用LADRC 控制器的系统输出。图8 的纵轴就表示“1”个单位值，无单位。

图8 LADRC 控制器和PID 控制器的对比仿真结果

由图8 的仿真对比结果可以看出，在系统不受任何干扰时，两种控制器的控制效果几乎无差异，如图8(a)所示，当在系统中加入外部干扰时，基于LADRC 控制器的系统依然能够无超调并快速到达稳态，而基于PID 控制器的系统超调量较大且到达稳态时间明显变长，在多次调节PID 控制器参数后输出曲线依然没有明显改善。因此，在抗干扰能力方面，基于LADRC 控制器的系统要比基于PID 控制器的系统更强。

在图4 所示光伏系统仿真模型的基础上，保持系统电路参数、仿真参数等参数不变，将PID 控制器替换成LADRC 控制器，得到光伏系统的仿真模型如图9 所示。

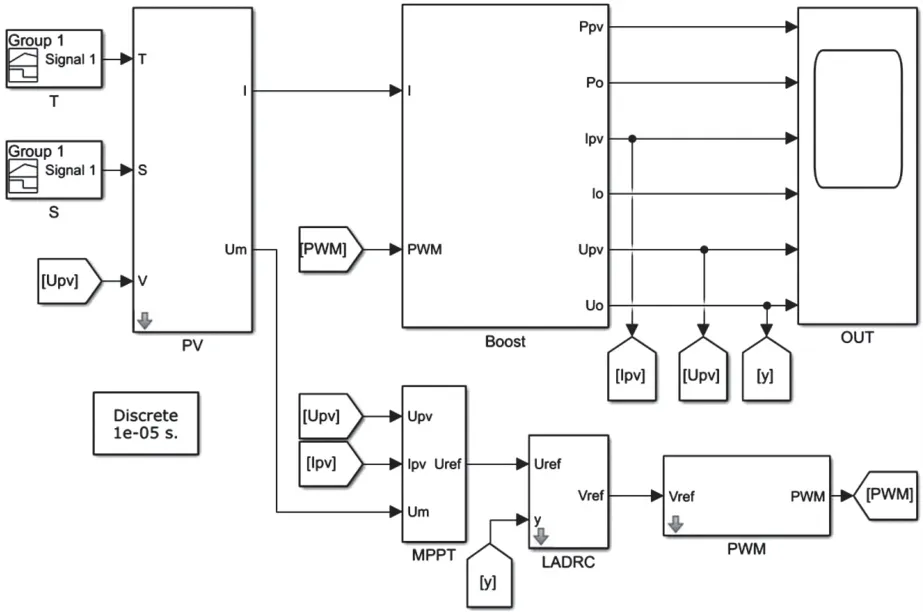
图9 基于LADRC 控制器的光伏系统仿真模型

3 仿真结果对比分析

2 000μF，升压电感L=1×10-2H，负载电阻R=

进行仿真验证并分析，电容C1和C2均取值为25 Ω，采样时间0.000 1 s，仿真步长设置为0.000 01 s，PID 控制器仿真参数为kp=0.1，ki=0.1，kd=0。设计额定输出功率为200 W 的光伏系统，其中LADRC 控制器需要整定的三个参数ω0、ωc、b0和光伏阵列参数如表3 所示。

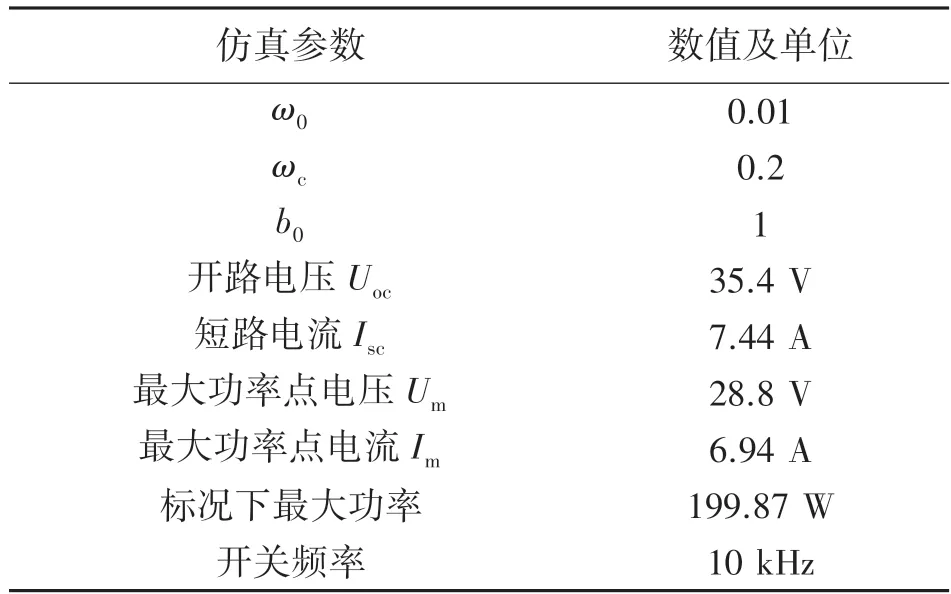
表3 仿真参数

在标况下对光伏系统进行仿真，分别得到光伏阵列侧输出功率如图10(a)所示，直流母线侧(Boost 电路输出侧)输出功率如图10(b)所示，曲线①代表的是采用LADRC 控制器的光伏系统，曲线②代表的是采用PID 控制器的光伏系统，下同。由图10(a)可以看出，曲线①到达稳态的时间要更短，在稳态时比较平稳，且稳态时曲线①浮于曲线②之上，功率振荡比曲线②小。由图10(b)可以看出，两条直流侧功率曲线在稳态时近似重合，但是应用LADRC 控制器的光伏系统到达稳态的时间更短，且在稳态时曲线①浮于曲线②之上，功率损耗更小。

图10 标况下的输出功率对比

对于光伏系统，S、T等均为影响系统输出功率的外部扰动，用两个Signal Builder 模块模拟随时间变化的S和T，详细参数变化如下:(1)在0 s～0.4 s时间段，设置S=1 000 W/m2，T=25 ℃；(2)在0.4 s～0.8 s 时间段，设置S=800 W/m2，T=15 ℃；(3)0.8 s～1 s 时间段，设置S=1 200 W/m2，T=60 ℃。

由图11 仿真结果可知，光伏系统约在0.1 s 左右达到稳态，曲线①浮于曲线②之上。在0 s～0.4 s时间段，图11(a)曲线①稳态时为199.9 W，曲线②为196.7 W，稳态功率相差3.2 W，图11(b)曲线①稳态时为195.7 W，曲线②为192.1 W，稳态功率相差3.6 W；在0.4 s～0.8 s 时间段，图11(a)曲线①稳态时为154.4 W，曲线②为153.9 W，稳态功率相差0.5 W，图11(b)曲线①稳态时为151.2 W，曲线②为150.2 W，稳态功率相差1 W；在0.8 s～1 s 时间段内，图11(a)曲线①在0.84 s 时刻到达稳态，稳态功率约为242.4 W，曲线②在仿真时间内未达到稳态，图11(b)曲线①稳态时为237.5 W，曲线②在慢慢上升，在1 s 时刻仍未达到稳态。

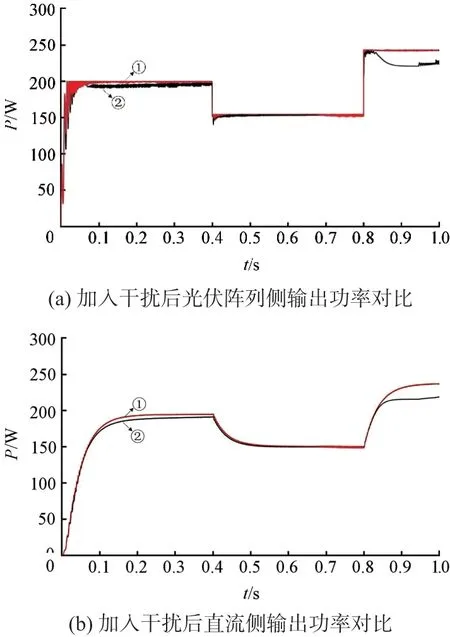
图11 加入不同的干扰后输出功率对比

4 结论

针对采用PID 调节的MPPT 控制器抗干扰能力不足，稳态时功率损耗较大的问题，提出一种采用LADRC 技术的MPPT 控制器，并在仿真中进行验证，得到结论如下:

(1)采用LADRC 技术的MPPT 控制器能够预测干扰并提前给出补偿，在面对外部干扰时(如S和T改变)，能够快速响应并达到新的稳态，功率损耗小。

(2)采用LADRC 控制器的光伏系统在到达最大功率点附近的功率振荡比采用PID 控制器的光伏系统小，过渡较平缓。