基于分组差分粒子群算法的含分布式电源配电网故障定位
赵冰杰,贾宏杰,李沐阳,侯 恺,高 晗,李 亮
(1.天津大学 智能电网教育部重点实验室,天津 300072;2.厦门理工学院 国际教育学院,福建 厦门361000;3.国网山西省电力公司晋中供电公司,山西 晋中 030600)
0 引言
目前,智能电网已经成为了世界各国关注的焦点[1],[2]。配电网处于电力系统的末端,直接向用户供电,且包含众多分布式电源,极易发生故障[3],[4]。配电网自动化系统应及时发现故障区间,隔离故障,恢复非故障区间的正常供电。其中最重要的难题就是发现和定位故障,因此在配网自动化基础上,研究含分布式电源的配电网故障定位 成 为 当 今 热 点[5],[6]。
粒子群算法是当下主流对含分布式电源的配电网故障定位算法[7]~[12]。文献[13]提出将粒子群算法应用到配电网故障区间定位中,但该算法存在未成熟时过早收敛的现象。文献[14]将粒子群算法和穷举法相结合,将配电网进行分层,对于维度大的配电网利用粒子群算法进行故障区间定位,对于维度小的配电网利用穷举法进行故障区间定位。该算法可有效解决早熟问题,但易使算法陷入局部最优。文献[15]将故障信息畸变修正策略与粒子群算法相结合,当馈线终端装置(Feeder Terminal Unit,FTU)上传的故障电流信息发生畸变,该算法可以正确分析所上传的电流信息,并给予修正。但是,该算法同样容易陷入局部最优,计算时间变长。文献[16]提出了差分粒子群算法,该算法通过差分算法和粒子群算法分别对种群进行寻优计算,最后选择目标函数值较小的个体作为种群最优解进入下一代进化计算。但是,该算法将两种算法并行计算,计算时间长,准确性降低。
本文将分组差分粒子群算法应用到配电网故障定位中。该算法首先将粒子群进行分组,然后更新每组粒子群的速度、位置以及个体历史最优值、全局最优值,最后对每组全局最优值进行变异、选择。完成上述操作,将分组粒子群融合成一个新种群,进行循环操作,直到输出最优解。与其他粒子群算法相比,本文算法避免易陷入局部收敛,且准确性和快速性得到提高。
1 配电网故障区间定位模型构建
在配网自动化系统中,通过FTU可监视配电网的运行状况,及时发现配电网故障,并对配电网故障进行区间定位。实现故障区间定位,首先应对配电网开关及故障区间进行状态编码,然后构建开关函数和目标函数[17]。
1.1 开关函数构建
配网线路区间只有正常和故障两种状态,因此,可对配网第x个线路区间状态Lx编码为

在传统的配电网中,潮流方向是单一的,当配网线路发生故障时,故障电流都是从系统电源侧流向故障点。但对于含分布式电源的配电网,当线路发生故障时,故障电流是从系统电源侧和分布式电源流向故障点。通过某个开关的故障电流可能有两个方向,定义从系统电源侧流向故障点的故障电流方向为正方向,因此可对配网第m个开关状态Fm编码为

开关函数表示了故障区间和开关状态的逻辑关系,本文研究了含分布式电源的配电网故障区间定位,需要考虑分布式电源的投切,因此本文定义开关函数为
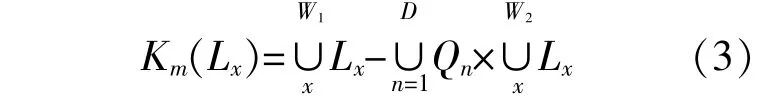
式中:Km为配网第m个开关期望状态值;Lx为配网第x个区间状态值;∪为或运算;W1为开关m下游区间数,即开关m到配网线路末端或到终端DG的线路区间数;W2为开关m上游区间数,即开关m到配网系统电源侧线路区间数;D为开关m下游DG个数;Qn为开关m下游第n个DG是否并网,当第n个DG并网,则Qn=1,当第n个DG未并网,则Qn=0。
1.2 目标函数构建
目标函数决定了粒子群算法搜索最优解的效果。目标函数不仅要适用于传统配电网,还应适用于含分布式电源的配电网。目标函数的建立须结合开关函数,其值越小,证明开关期望状态值Km与开关状态实际值Fm的偏移程度越小,因此,针对配电网故障区间定位传统的目标函数为

式 中:Lx为 配 网 区 间 状 态 量;Km(Lx)为 开 关 期 望 状态量;Fm为开关状态实际量;b为配网开关数。目标函数值Z(Lx)≥0,其值越小证明算法结果越准确,当Z(Lx)=0时,得 到 最 优 解Lx。
当FTU上传的电流信息Fm发生畸变时,会造成故障区间的误判,常用的处理方法是对Fm进行信息矛盾判断,但是该方法增加了算法的计算量。本文直接计算Z(Lx)的值,当Fm有n个畸变量时,Z(Lx)≥n。式(4)可 能 存 在 配 电 网 故 障 区 间 误判情况。将式(4)改进为

式中:λ为开关函数误判项,λ取值0.5;c为配电网区间数。此时目标函数值Z(Lx)≥0.5+n,n为畸变量。
经式(5)处理后,可消除误判情况。
2 分组差分粒子群算法原理
2.1 分组粒子群算法原理
PSO(Particle Swarm Optimization)算 法 开 始 时生成初始解,N个粒子在M维空间中寻找最优解。含分布式电源的配电网故障区间定位,可利用二进制粒子群算法实现[18]。在二进制粒子群算法中,粒子的位置LOX取值为0或1;粒子的速度VOX即LOX取0或1的概率,速度VOX越大,LOX取1的概率越大,反之LOX取0的概率越大。速度和位置的关系可通过sigmoid函数表示。因此,二进制粒子群算法的速度更新公式和位置更新为

式中:r为收缩因子;ω为惯性因子;k1,k2为学习因 子;d1,d2为(0,1)内 的 随 机 数;LOXbest1(t)为 个 体历 史 最 优;LOXbest2(t)为 种 群 全 局 最 优;COX(t+1)为[0,1]内 的 随 机 数。
对于粒子群算法,学习因子k1,k2可直接决定速度更新公式的收敛程度。当k1较大时会造成粒子群在局部徘徊,当k2较大时会使粒子群陷入局部最优。此外,当个体粒子在个体历史最优和全局最优接近时,更新速度变得极其缓慢。本文在粒子群算法中引入分组概念,对粒子群算法进行改进。
首先计算N个粒子的目标函数值,从小到大排序,将N个粒子每隔f个粒子分为h组,即:

按照上述排序对粒子群再进行分组,式(10)中目标函数最大值分为一组,第二大值分为一组,以此类推,最小值分为一组,即:
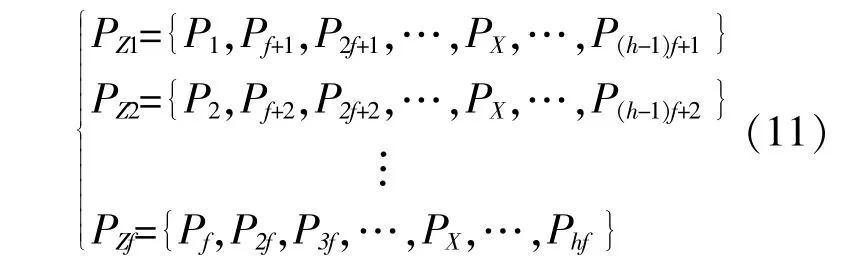
通过上述分组,原粒子群分为f组,每组均可代 表 原 种 群 的 特 性,然 后 通 过 式(6),(7)对 分 组 粒子群进行速度和位置更新。当分组粒子群寻优结束后,再将分组粒子群融合成一个种群进行目标函数排序,进行第二次寻优,直到寻优结束。通过分组粒子群寻优,可以保证原粒子群的种群多样性的延续,不易使种群陷入局部最优,使粒子群算法的准确性和容错性得到提高。
2.2 差分算法原理
为了进一步避免粒子群陷入局部最优,本文引入差分算法。
首先确定分组粒子群中的最优粒子Pbest,并随 机 选 取 两 个 粒 子Pb1,Pb2进 行 变 异 操 作。Pbest,Pb1,Pb2在M维空间中的位置为

确定Lb1,Lb2的海明距离h,计算Lbest需要变异的维数m。

式中:H为缩放后的海明距离;s为缩放因子,s取值 为[0,2]随 机 数;rand[0,1]为[0,1]内 的 随 机 数;int(H)为H向 下 取 整 数。
通过式 (15)计算得到Lbest需要变异的维数m,然后对Lbest的m维进行变异,若m维Lbest为1,则 变 异 成0;若m维Lbest为0,则 变 异 成1,得 到变异粒子Lb。
最后对变异粒子Lb和最优粒子Lbest进行选择操作。
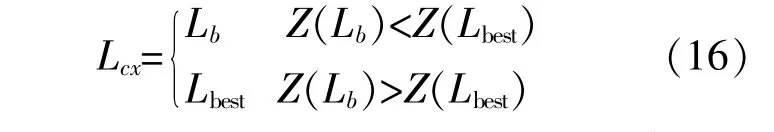
式 中:Z(Lb)和Z(Lbest)为 粒 子 的 目 标 函 数 值,选 择目标函数值较小的粒子作为下一代粒子个体Lcx。
2.3 算法求解流程
通过分析分组粒子群算法和差分进化算法,可得到基于混合算法的配电网故障区间定位方法的求解流程,如图1所示。
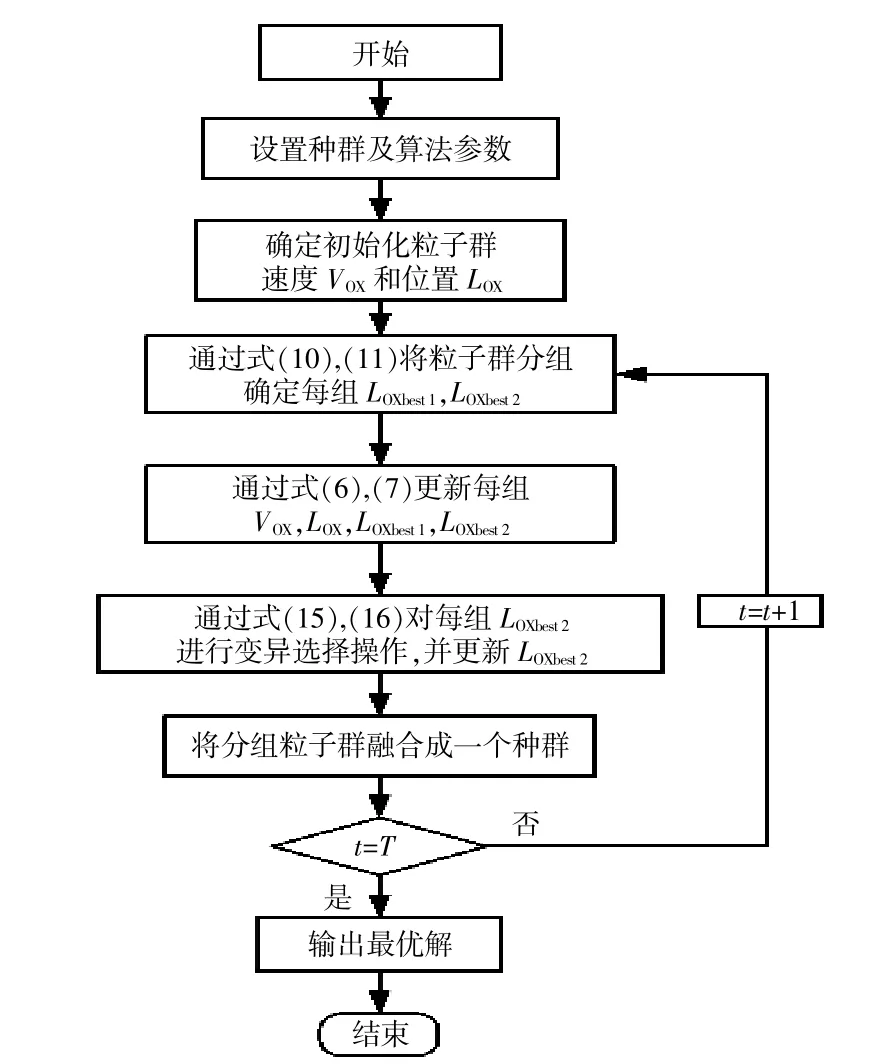
图1 分组差分粒子群算法流程图Fig.1 The flow chart of packet difference particle swarm optimization
图中:N为种群规模;T为迭代次数,初次迭代次数t=1;ω为惯性系数;λ为误判系数。
3 算例分析
本文以图2含光伏、风电的IEEE33节点系统为例进行仿真测试,对分组差分粒子群算法、粒子群算法、遗传算法、蚁群算法、退火算法进行了对比分析。本文设置故障包含了DG是否并网、FTU上传信息发生畸变、单个或多个故障区间等各种情况。实际工程中配电网故障90%以上均为单相接地故障,因此本文的故障特指该类故障。
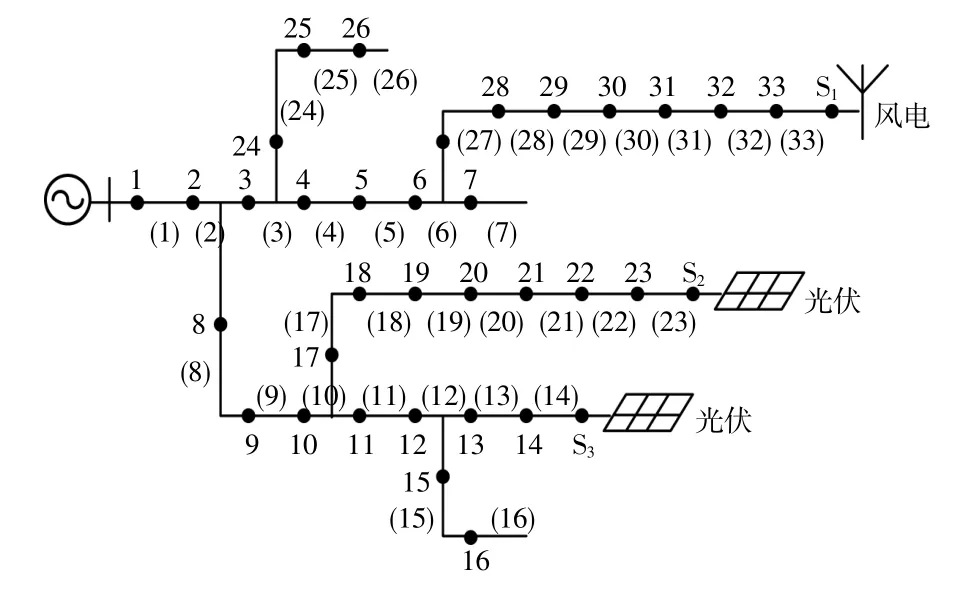
图2 含分布式电源的配电网系统Fig.2 Distribution network system with distributed power supply
本文分组差分粒子群算法参数设置如下:种群规模N=50,迭代次数T=50,学习因子k1=k2=2.3,惯 性 系 数 ω=0.5,f=5,h=10,误 判 系 数 λ=0.5,缩放因子s=0.8,目标函数初始值Z=5。算法寻优代数对比如图3所示。故障类型如表1所示。算法定位结果如表2~6所示。配电网拓扑如图4所示。

图3 算法寻优代数对比Fig.3 Algorithm optimization algebra comparison

图4 配电网拓扑图Fig.4 Distribution network topology diagram

表1 故障类型Table1 Fault type
由表2~6可知,通过对比多种算法的寻优结果,分组差分粒子群算法的准确性和快速性均得到极大提高,同时该算法可以改善其他算法陷入局部最优的不足。

表2 分组差分粒子群算法定位结果Table2 The result of packet difference particle swarm optimization

表3 粒子群算法定位结果Table3 The result of particle swarm optimization

表4 遗传算法定位结果Table4 The result of genetic optimization

表5 蚁群算法定位结果Table5 The result of ant clony optimization

表6 退火算法定位结果Table6 The result of simulated annealing optimization
分组差分粒子群算法是在粒子群算法的基础上引入差分算法和分组概念,算法每次迭代计算时间变长,但是相较于上述其他算法,分组差分粒子群算法的寻优代数可控制在20次以内,迭代次数明显降低。对于IEEE33节点配电网系统,分组差分粒子群算法的迭代次数可降低到30次,从而提高了故障定位的寻优速度。此外,将分组差分粒子群算法应用到实际工程中时,面对复杂的配电网系统,该算法可能在已设置的迭代次数中无法计算出准确的结果,因此可以通过提高算法迭代次数来提高算法的计算准确率。相较与其它算法,在同时增加迭代次数的基础上,分组差分粒子群算法仍能保证准确性和快速性。
本文依托配网自动化平台对分组差分粒子群算法进行了验证,图5为实验结果。实验设置故障区间为S9~S13,通过该算法计算得到的故障区间介于S9配电开关和S13配电开关之间,进一步验证了该算法应用于实际工程的可行性。

图5 实验结果Fig.5 Experimental resul
4 结论
针对粒子群算法在含分布式电源的配电网故障定位时易陷入局部最优的问题,本文提出了分组差分粒子群算法,该算法通过分组思想,巧妙的将差分算法应用到粒子群算法中。仿真算例表明,分组差分粒子群算法的寻优迭代次数明显降低,跳出局部最优的能力极强,准确性和快速性得到提高。最后通过配网自动化平台对所提算法进行了验证,进一步证明了该算法应用于实际工程的可行性。

