输电线路内悬浮抱杆起升动载系数的研究

马 勇，夏拥军，孟凡豪，孙立江，安 平，龚 岩

（1.中国电力科学研究院有限公司输变电工程研究所，北京 100055；2.国网甘肃省电力公司建设分公司，兰州 730050）

随着经济社会的发展，电力行业在人们的生产生活中发挥着越来越重要的作用。2020年我国成为电力需求量第二大的经济体，但我国电力资源地域分布不均匀，往往需要进行远距离大功率的电力输送。电力抱杆是一种为了满足架设输电线路需求的格构式起重机械[1-2]，其中悬浮式抱杆因其结构简单，使用安装方便得到了广泛的应用[3-5]。相关学者对电力抱杆的动态特性展开了研究。叶立运等[6]采用计算机辅助技术对内悬浮外拉线抱杆组立1 000 kV 耐张塔进行了分析；张谦等[7]基于非线性有限元方法，对组塔施工内悬浮内拉线抱杆结构进行了仿真计算分析；徐金城[8]等人利用ANSYS 仿真软件对悬浮抱杆的风振响应进行了分析，发现抱杆中部振幅最大，安装过程中应对加强中部标准节的连接；赵红波[9]利用回归分析，研究了风载荷对悬浮抱杆的影响。现有的悬浮抱杆动态特性相关研究主要集中在风载荷的影响，研究形式主要以有限元仿真为主，而悬浮抱杆对吊件的起升存在冲击作用，目前尚未研究，导致内悬浮抱杆的使用及计算选型存在一定安全风险。本文对悬浮抱杆的起升动载系数进行研究，首先建立悬浮抱杆的空间结构动力学模型，利用刚度和位移的关系求解等效刚度，利用动能等效的原理求解等效质量，之后根据等效刚度和等效质量的求解结果得到起升动载的表达式，最后通过ANSYS有限元仿真验证表达结果的正确性。

1 研究对象的选取

抱杆是特高压及各电压等级电网的重要组塔施工装备之一，针对不同的载荷需求、不同的施工环境，可选择的抱杆有内悬浮抱杆、人字抱杆、落地摇臂抱杆与落地平臂抱杆等。其中，内悬浮抱杆因结构简单、重量轻、运输方便等优点被广泛应用。按照拉线形式，内悬浮抱杆分为内悬浮外拉线抱杆与内悬浮内拉线抱杆，分别如图1（a）与图1（b）所示。内悬浮外拉线抱杆是把抱杆的拉线锚固在地面设置好的地锚上，抱杆的稳定性好，安全性高；内悬浮内拉线抱杆是把抱杆的拉线锚固在已组好的铁塔主材上，由于铁塔为桁架结构，具有一定的弹性，且内拉线方式使得抱杆吊装工作时倾斜角度小，对控制绳的要求高，安全性与稳定性较差。因此，内悬浮外拉线抱杆更具有普遍性，故选取内悬浮外拉线抱杆（简称悬浮抱杆）作为研究对象。

图1 悬浮抱杆工作示意图

2 刚度和质量的分析

悬浮抱杆未受载时由抱杆和拉索组成，抱杆的长度为L，四根拉索在空间中均匀分布，长度相等，抱杆和拉索与地面之间全部为铰接。悬浮抱杆受载时，其中两根拉索放松，结构由另外两根拉索和抱杆组成，如图2所示。抱杆与空间z轴的夹角为γ，拉索与xOy平面的夹角为α，两根拉索之间的夹角为2θ，且拉索平面与xOy平面之间的夹角为β。

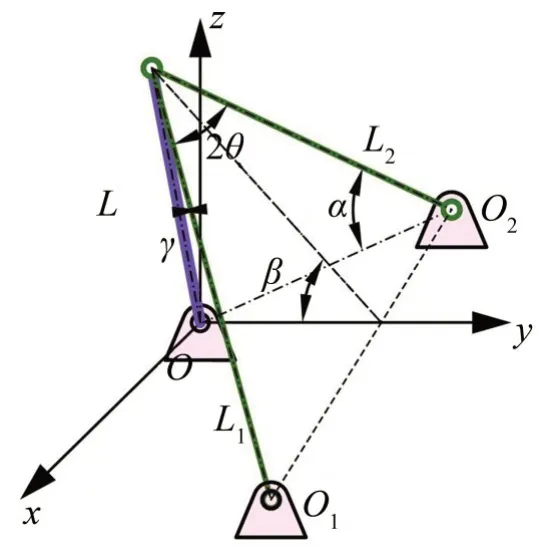
图2 悬浮抱杆的几何结构

2.1 刚度的等效

在吊点处施加竖直向下的力F,设拉索中的张力分别为T1、T2，抱杆中的轴力为N，悬浮抱杆的受力情况如图3所示。

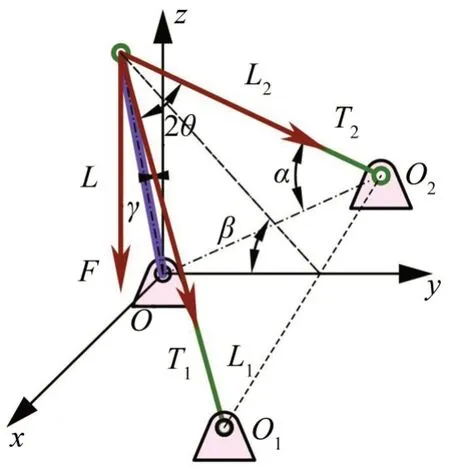
图3 悬浮抱杆的受力情况

在拉索平面内对拉索的张力进行合成，如图4（a）所示，拉索张力的合力为T=2T1cosθ。在yOz平面内进行力的分解，如图4（b）所示。

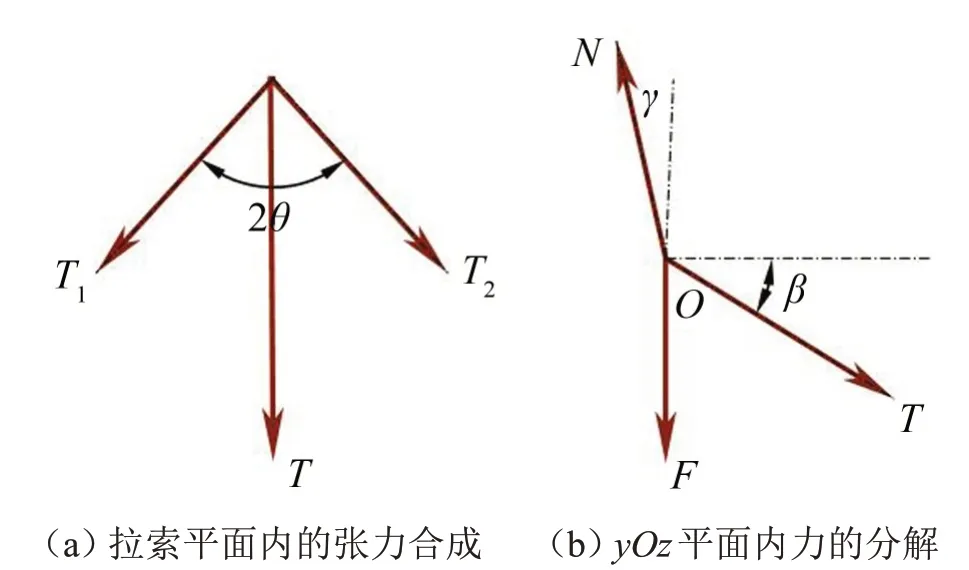
图4 悬浮抱杆受力分析

根据力的平衡条件∑F=0，得到悬浮抱杆的静力学平衡方程如式（1）所示。

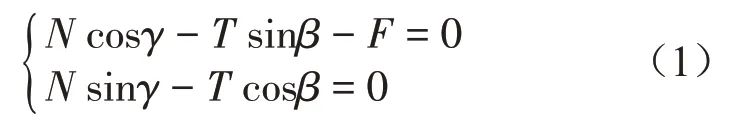
求解方程组，求解结果如式（2）所示。

设单侧拉索的横截面积为A1，弹性模量为E，起重臂的横截面积为A，弹性模量为E。根据结构力学的相关知识，吊点处受力后的位移如式（3）所示。

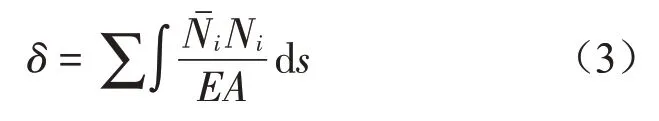
代入相关数值，得到悬浮抱杆在F作用下吊点处的位移如式（4）所示。

2.2 质量的等效

假设悬浮抱杆受载后结构发生微小变形，角度变化Δγ，则抱杆与xOy平面的夹角为γ+Δγ。根据图2 可知，悬浮抱杆各个单元体的绝对位置矩阵分别如式（5）至式（7）所示。

各个单元体相对位置与绝对位置的关系如式（8）所示。

当Δγ→0 时，cosΔγ≈1，sinΔγ=，各个单元体绝对位移矩阵与位置矩阵的关系如式（9）所示。

单元体相对位移矩阵与绝对位移矩阵的关系如式（10）所示。根据式（5）至式（10），各个单元体的相对位移矩阵如式（11）至式（12）所示。

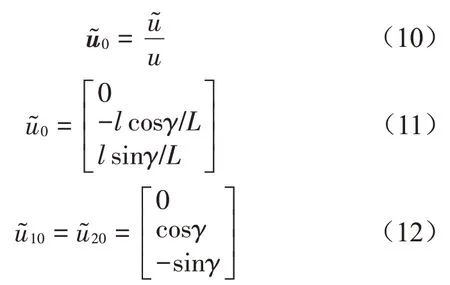
悬浮抱杆等效质量如式（13）所示。

悬浮抱杆的吊点位于拉索和起重臂的铰接点，因此等效相对位移，悬浮抱杆的等效质量如式（14）所示。

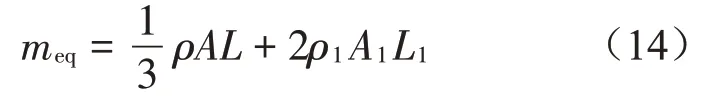
3 起升动载系数的表达与验证

3.1 动载系数的表达

建立悬浮抱杆起升动力学模型，进行求解，起升动载系数的表达式如式（15）所示。

在实际工程问题中，钢丝绳的刚度和结构位移不易直接求得。设与载荷相连的钢丝绳的弹性模量为EQ，长度为LQ，单根钢丝绳的截面积为A0，钢丝绳的倍率为a，则钢丝绳的刚度可以表示为，因此，悬浮抱杆的起升动载系数可以用式（16）表示。其中，钢丝绳的弹性模量可根据GB/T 24191-2009《钢丝绳实际弹性模量测定方法》测量得到，对于重要的钢丝绳，可要求钢丝绳生产厂家提供。

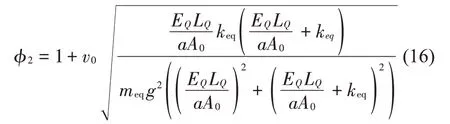
3.2 有限元仿真验证

选择□800型悬浮抱杆进行有限元验证。□800型悬浮抱杆长度为43.4 m，标准节外径宽800 mm，主弦采用了∟100×8 角钢，斜腹杆采用∟56×5 角钢。拉索钢丝绳和起升钢丝绳均选单倍率ϕ15.5 6×19交绕型纤维芯钢丝绳。初始状态拉索与地面之间的夹角α=45°，起升载荷时抱杆与竖直方向的最大夹角γmax=10°。

由式（4）、式（15）及式（16）可得□800 型悬浮抱杆的等效刚度为2.06×104N/m，等效质量为1.53×103kg，起升动载系数的表达式为ϕ2=1+0.265v0。

利用ANSYS建立悬浮抱杆的有限元模型，在拉索与地面连接处施加全约束，在抱杆根部施加铰接约束，在吊点处施加静载10 kN，悬浮抱杆的位移如图5所示，□800型悬浮抱杆的静位移为0.028 9 m。

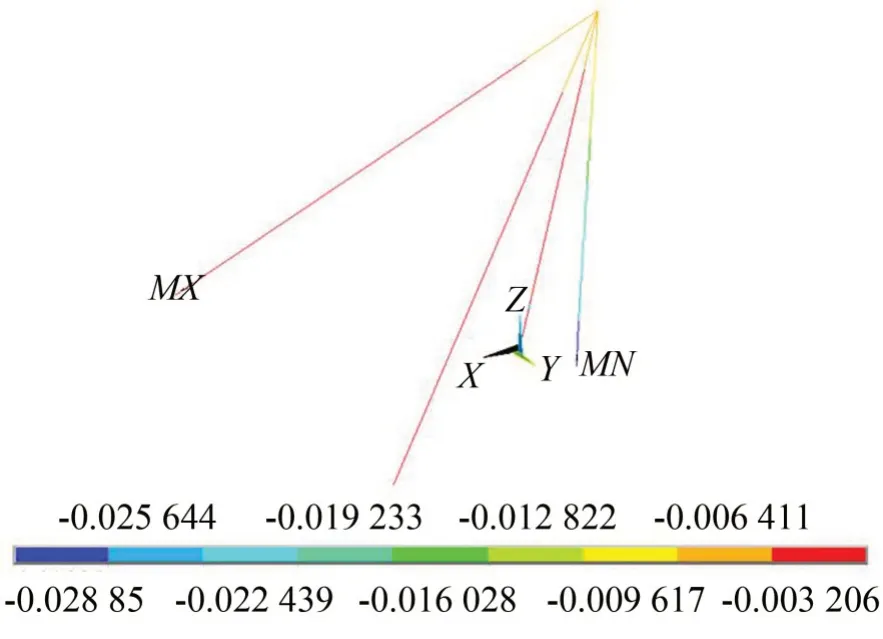
图5 50 kN静态载荷下悬浮抱杆的位移情况

对悬浮抱杆分别施加不同的外力，使其以不同的起升速度进行起升，使用ANSYS进行瞬态动力学分析，吊点处位移随时间的变化如图6所示。

图6 不同起升速度吊点位移随时间变化

将不同起升速度下吊点最大位移的有限元仿真结果进行整理，如表1所示；将理论值与仿真值进行比较，如图7所示。

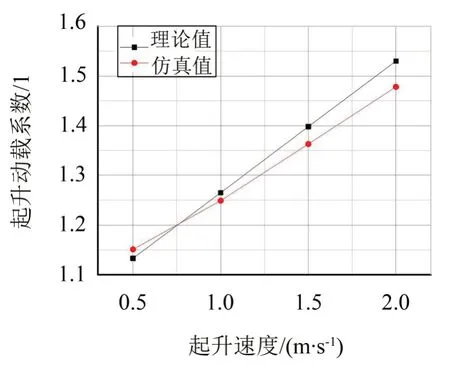
图7 起升动载系数理论值与仿真值比较

表1 不同起升速度起升动载系数仿真结果

由有限元仿真结果可知，对于□800 型悬浮抱杆，起升动载系数的理论值与仿真值误差很小，起升动载的表达式能够很好地反映其起升动载特性。

4 结语

本文对悬浮抱杆的起升动载系数进行了研究。悬浮抱杆的质量和刚度是影响悬浮抱杆起升动载系数的决定性因素。本文建立了悬浮抱杆的模型，对悬浮抱杆的结构进行分析，利用结构变形与刚度的关系求解了悬浮抱杆的等效刚度，分别求解出各个单元体的位置矩阵和位移矩阵，利用动能等效的原理求解出悬浮抱杆的等效质量。对起升动力学模型进行求解，得到起升动载系数的表达式，并对表达式进行优化，得到更有利于工程应用的形式。

随后应用有限元软件ANSYS 对悬浮抱杆的起升过程进行仿真，建立了□800型悬浮抱杆的模型，分别以0.50 m/s、1.00 m/s、1.50 m/s 和2.00 m/s 的速度进行起升，求解其最大动位移，获得不同起升速度的起升动载系数。将仿真值与理论值进行比较，发现二者误差很小，由此证明悬浮抱杆的起升动载系数的表达式能够很好地反映其起升动态特性，为今后悬浮抱杆的设计计算提供了一定的参考。