高压直流输电系统直流谐波阻抗的解析计算及谐振分析研究

李 欢，傅 闯，辛清明，代书龙，赵晓斌

高压直流输电系统直流谐波阻抗的解析计算及谐振分析研究

李 欢，傅 闯，辛清明，代书龙，赵晓斌

(南方电网科学研究院有限责任公司直流输电技术国家重点实验室，广东 广州 510663)

研究了常规高压直流输电系统直流回路谐波谐振问题。采用解析计算的方法，对典型高压直流输电系统的直流回路谐波阻抗进行数学建模。基于状态空间模型得到了直流谐波阻抗的解析表达式，形成了直流回路阻抗频谱，并通过PSCAD软件对所提模型进行了验证。分析了系统各环节参数与直流谐波阻抗的耦合关系。提出了采用调整控制参数实现直流回路谐振宽频抑制的方法，并通过电磁暂态仿真对所提方法进行了验证。结果表明，所提方法可有效提升高压直流系统的直流谐振抑制能力和安全稳定运行水平。

高压直流；直流谐波阻抗；解析计算；谐振分析

0 引言

高压直流输电技术因其具有传输距离远和容量大等优点而广泛应用于国内外电网[1-4]，在我国西电东送和新能源消纳中也发挥着重要作用[5-8]，且高压直流工程的数量呈逐年增加的趋势[9-11]，直流工程的稳定运行对整个电网的安全稳定起着越来越重要的作用。而谐波谐振问题是影响直流稳定的一个重要因素，并已有较多研究[12-18]。近期发生了因雷击直流线路而引发直流谐振并最终导致直流闭锁跳闸的事故，进一步引起了业界对直流谐振问题的关注。直流回路谐波谐振的原因主要是直流回路阻抗在敏感频率点附近存在谐振点，导致直流回路该频率的谐波放大甚至振荡，当电压电流超过设备定值时触发系统保护跳闸。所以要避免直流谐波谐振，首先要得到直流系统的直流谐波阻抗频谱，然后对阻抗频谱进行谐振点分析，最后对存在的阻抗谐振点采取措施，调整或消除谐振点。

在直流谐波阻抗计算方面，主要有仿真分析法和解析计算法。仿真分析法是在PSCAD/EMTDC等电磁暂态仿真软件中，搭建高压直流系统的详细仿真模型，然后采用测试信号法或单位冲击电压源法等方法来进行仿真计算，通过对仿真结果处理并得到直流谐波阻抗[19-22]。这些方法可对高压直流系统进行精细准确建模，在工程中也得到了成功应用。

解析计算法通过建立直流系统的数学模型并推导出直流回路的谐波阻抗解析表达式，通过该表达式进行频域变换直接得到直流谐波阻抗频谱，该方法不依赖于电磁暂态仿真，计算速度快，且便于进行参数化的分析和设计，但由于直流系统包括半导体开关和控制系统等非线性环节，元器件较多，精细的解析建模难度较大，现有研究一般都进行了一定简化或近似处理，如文献[23-24]采用三脉动电压源等效建模，将LCC换流器等效为谐波电压源进行近似计算，且未考虑控制系统的影响，文献[25-26]采用开关函数的方法对换流器直流谐波阻抗进行建模，但是在建模过程中忽略直流工程的控制系统作用，文献[27]采用谐波线性化的方法，考虑了控制环节影响，但只考虑了整流站或逆变站的单站阻抗，未考虑整体直流回路阻抗、线路和直流滤波器等的影响。

在直流谐波谐振抑制方面，现有方法主要是在直流系统中加装谐波抑制设备，如加装阻波器[28-29]或有源滤波器[30-36]等，这些方法可直观可靠改变系统的直流谐波阻抗，在工程中也得到了成功应用。也有采用有源滤波器实现谐振抑制的，该方案需要采用全控半导体器件，其成本一般较高，控制策略也比较复杂，对设计和运维要求较高，我国±500 kV天广直流工程直流滤波器就配置有源滤波器，但投运出现问题较多，很快将有源部分旁路，后来被拆除了。

本文采用解析计算的方法，对高压直流输电系统的直流回路谐波阻抗进行数学建模，模型中统一考虑了交流电网、交流滤波器、换流器开关、控制系统、直流滤波器和直流线路等各环节的动态特性，得到了直流谐波阻抗的解析计算频谱曲线。分析了系统各环节参数与直流谐波阻抗的耦合关系，提取了影响直流谐波阻抗的关键参数，基于系统关键参数提出了直流回路谐振的宽频灵活抑制方法，并通过电磁暂态仿真验证了所提方法的可行性。

1 典型高压直流系统

高压直流系统一般采用12脉动换流器为一个基本单元，本文以单极大地运行的两端直流为例进行研究，图1为典型的高压直流输电系统的原理框图。其包括整流侧、逆变侧和直流回路3部分。整流侧和逆变侧的结构相似，主要包括：交流电网、换流变、换流阀、交流滤波器、控制器和锁相环。

图1 典型高压直流输电系统原理框图

交流电网为戴维南等值电路，由交流电压源ac、内电阻s和内电感s串联组成；换流变包含T1和T2两组换流变；换流阀由两组6脉动晶闸管换流器串联组成；交流滤波器由相应的电容电感电阻元件串并联组成，控制系统部分整流侧为定电流PI控制，逆变侧为定电压PI控制；整流站和逆变站的锁相环PLL均为同步参考坐标锁相环，其原理框图如图2所示。

图2 锁相环原理框图

直流回路部分包括直流线路、直流滤波器和平波电抗器，直流线路选取级联π型电路等效，级联个数为4个。图1中系统各参数如表1所示[37]。

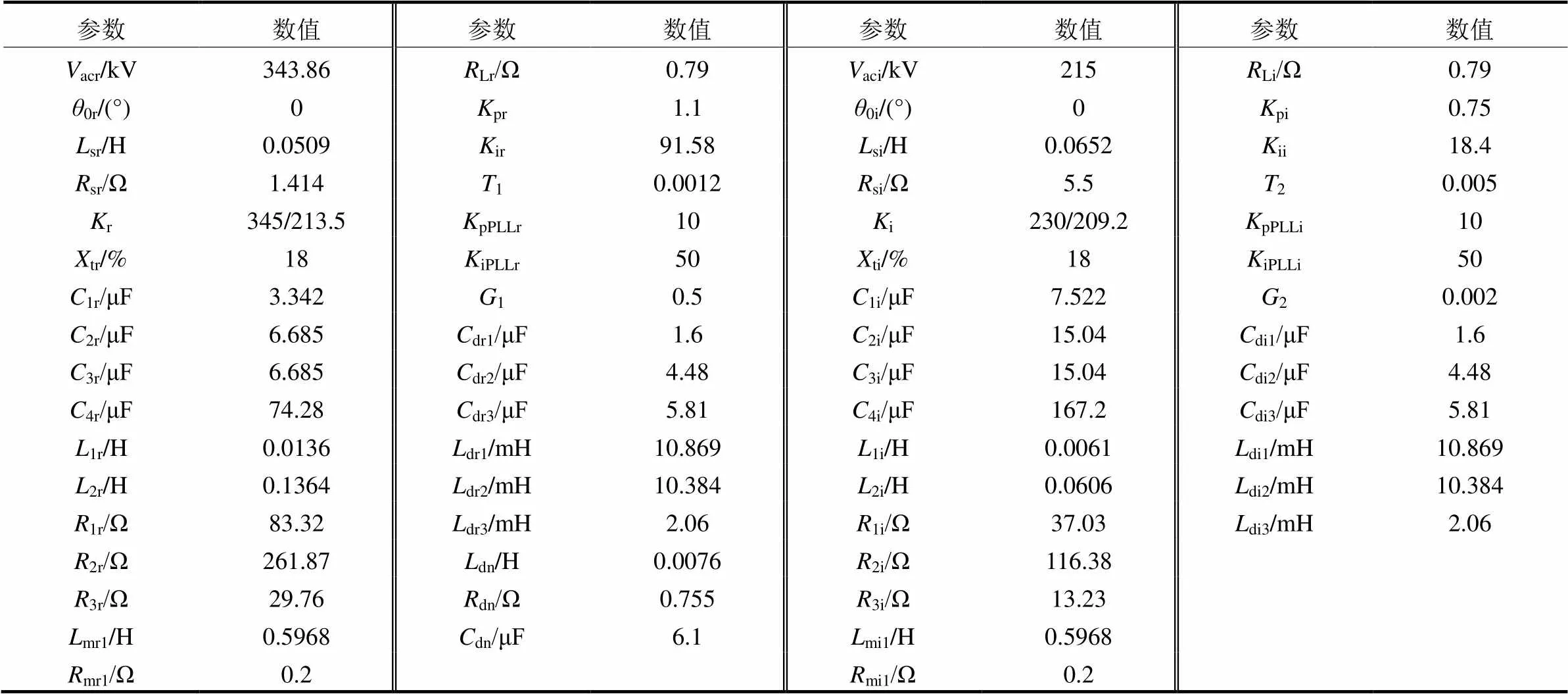
表1 系统主要参数

2 高压直流系统直流回路谐波阻抗模型

根据图1所示的高压直流系统的结构，分别建立一次系统和二次控制系统的数学模型，并通过电气和控制等相关参数进行耦合。主要原理和逻辑框图如图3所示。

由图3可知，图1所示的高压直流系统可由1到62共62个微分方程组成的微分方程组来描述其系统动态特性。微分方程组对应的自变量矩阵为

交流系统的电压电流为三相正弦交变量，为便于建模，将其进行变换，得到相应的恒定分量，形成图3中交流系统的微分方程，电网等效电感sr中电流sr的微分方程为

交流系统其他变量的微分方程详见附录。

换流阀因包含非线性晶闸管器件，对其采用基于开关函数的方法建立基频模型，可得其网侧交流电流的分量为

图3 高压直流系统数学模型框图

Fig. 3 Mathematical model block diagram of HVDC system

控制系统均将积分环节的输出作为其微分方程自变量，并根据控制环节构建其动态方程，典型方程为

由于式(3)中包含非线性函数，为便于分析，将1到62在额定工作点进行局部线性化，得到直流系统的小信号状态方程为

式中，状态变量矩阵如式(1)所示；为输入变量矩阵；状态矩阵和输入矩阵的表达式为

式中，为矩阵的维数。

式(5)为高压直流系统的小信号状态方程的时域表达式，为了便于对直流回路各频率点的谐波阻抗进行解析建模，将式(5)进行拉普拉斯变换，得到高压直流系统频域的解析表达式，如式(8)所示。

3 直流回路阻抗仿真验证

为验证上述模型，本节分别建立了直流回路阻抗的解析计算模型和电磁暂态模型进行对比验证。其中解析计算模型需对式(1)—式(11)进行联立求解，由于涉及到矩阵运算和状态方程求解，矩阵维数高，手动求解效率低，而Matlab具有较好的矩阵运算能力，所以本文利用Matlab/M语言基于式(1)—式(11)开发了图1直流系统的直流谐波阻抗解析计算程序，并根据表1的参数由所建解析计算程序得到了直流系统整流侧平抗处的直流回路谐波阻抗频谱曲线，如图4中黑色曲线所示。

图4 整流侧平抗出口处直流谐波阻抗频谱

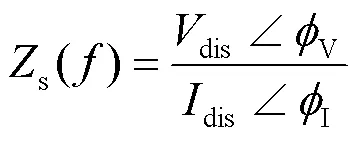
由式(12)可得整流侧平抗出口处各频率点的谐波阻抗幅值和相位，如图4中红色圆圈所示。

由图4可见，由PSCAD详细电磁暂态仿真计算的谐波阻抗(红色圆圈)与由Matlab基于解析计算所得的谐波阻抗曲线吻合较好，证明了本文所提模型的准确性。

4 高压直流系统直流回路谐振特性分析

由式(11)可知，直流谐波阻抗跟、和3个参数有关，其中为谐波源位置代号，和与直流系统的一次系统和二次系统的系统参数紧密相关。下面分别详细研究谐波源位置和系统参数对直流谐波阻抗和谐振特性的影响，其中系统参数较多，根据参数所处位置可分为：1) 直流回路参数；2) 两站控制系统参数；3) 两站交流系统参数。这些因素对高压直流系统的直流回路谐振的主要影响特性如下。

4.1 谐波源位置的影响

图5为整流站和逆变站的平抗出口处直流谐波阻抗特性对比分析情况，图中黑色曲线为整流侧平抗出口阻抗曲线，红色曲线为逆变侧平抗出口阻抗曲线。

图5 整流侧和逆变侧平抗处谐波阻抗曲线

由图5可知，整流侧和逆变测的直流谐波阻抗曲线整体轮廓相近，尤其在300 Hz以上的高频部分，曲线基本重合，300 Hz以内的低频部分，整流侧和逆变测的阻抗曲线均有一个阻抗值较低的谐振风险点，但两侧的谐振风险点的频率不同，整流侧的谐振频率在30 Hz左右，逆变测的谐振频率在70 Hz左右，所以整流侧和逆变侧需针对两个不同的频率对直流谐波阻抗进行统一协调设计，以同时减小两侧的谐振风险。

4.2 系统参数的影响

4.2.1直流回路参数的影响

直流回路主要由直流线路和直流滤波器两部分构成，下面分别分析两部分参数的影响。

4.2.1.1直流线路参数的影响

由图6可知，当直流线路参数由电缆调整为架空线路后，谐波阻抗特性发生了较大改变，其中谐波阻抗的高频部分变化较小，但中低频部分发生了较大改变，出现多个局部阻抗低值点，所以直流线路型式不同时，直流谐波阻抗特性差别较大，需进行针对性设计。

图6 整流侧平抗处直流阻抗跟直流线路型式的关系

4.2.1.2直流滤波器的影响

实际运行中，存在直流滤波器投入和退出的情况，其对直流谐波阻抗的影响如下。

图7为两侧DCF投入和退出时整流侧平抗处阻抗的曲线，其中黑色曲线为两侧直流滤波器均投入时的阻抗曲线，红色曲线为整流侧直流滤波器退出时的曲线，绿色曲线为逆变侧直流滤波器退出时的曲线。

两侧直流滤波器的投入和退出对整流侧和逆变测的直流谐波阻抗影响较小，主要是300 Hz以上的高频部分发生了较小波动，300 Hz以内的低频部分基本没有影响。

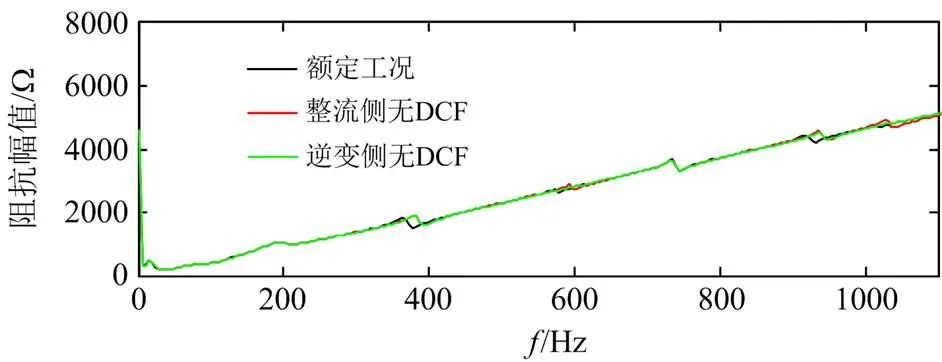
4.2.2两站控制系统参数影响

4.2.2.1控制系统延时参数的影响

实际控制系统中，测量环节、控制器和线缆等存在一定延时，下面分析控制系统的延时对直流谐波阻抗的影响，延时环节为非线性环节，本文采用泰勒级数展开来近似等效延时环节，以整流站和逆变站控制系统的延时均为5 ms时整流侧平抗出口处谐波阻抗为例进行分析。

泰勒级数展开的阶数越高，则近似计算的精度越高，但计算量也越大，下面首先探讨展开级数跟计算精度的关系，图8显示了延时为5 ms时整流侧平抗出口阻抗频谱，其中红色圆圈为PSCAD/ EMTDC仿真所得精确阻抗点，黑色曲线、蓝色曲线和红色曲线分别为采用一阶泰勒展开、二阶泰勒展开和三阶泰勒展开等效计算得到的阻抗曲线。可见采用一阶和二阶展开时，误差较大，采用三阶展开时阻抗计算结果跟PSCAD/EMTDC仿真结果相近，表明采用三阶泰勒展开来等效延时环节可满足计算要求。

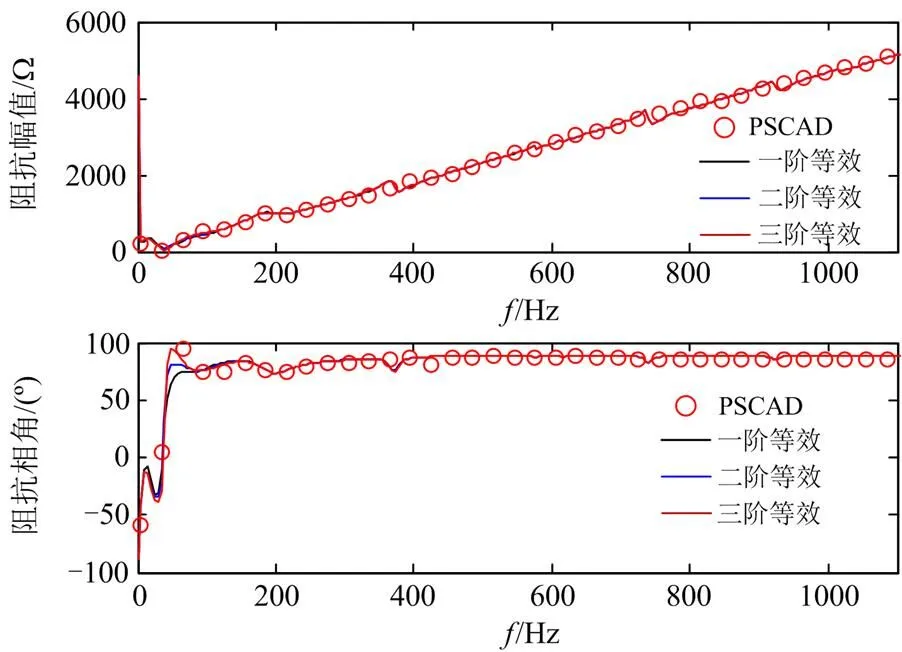
图8 整流侧平抗处直流阻抗跟延时环节泰勒展开阶数的关系

下面以三阶泰勒级数来近似延时环节，得到逆变侧平抗出口阻抗跟延时的关系如图9所示，其中黑色曲线为无控制延时的曲线，红色曲线为整流侧和逆变测均有5 ms控制延时的曲线，可见延时环节主要影响阻抗的低频部分，由图9中局部放大图可见在40 Hz附近阻抗幅值发生了较大跌落，可见控制系统的延时环节时间越长，谐振风险越大。

图9 逆变侧平抗处直流阻抗跟控制系统延时的关系

4.2.2.2两站控制系统PI参数的影响

下面分析两站控制系统的参数对直流谐波阻抗的影响，以整流侧平抗出口处直流谐波阻抗为例进行分析。

1) 整流站控制参数对整流侧直流谐波阻抗的影响

首先分析整流侧控制参数对整流侧直流谐波阻抗的影响，整流侧控制系统参数pr和ir从额定值增大时，直流谐波阻抗的曲线变化情况如图10和图11所示。

由图10和图11可见，整流侧控制系统参数对整流侧平抗出口谐波阻抗的低频段影响较大，当pr和ir增大时，谐波阻抗频谱的原谐振点处阻抗逐渐升高，但当参数增大到一定程度时，阻抗频谱在原谐振点的附近频率处开始产生新的谐振点，所以整流侧控制参数对整流侧平抗处谐波阻抗的影响不是单调的，而是随频率不同呈现不同的特性，设计时需根据敏感频带不同做差异化设计。

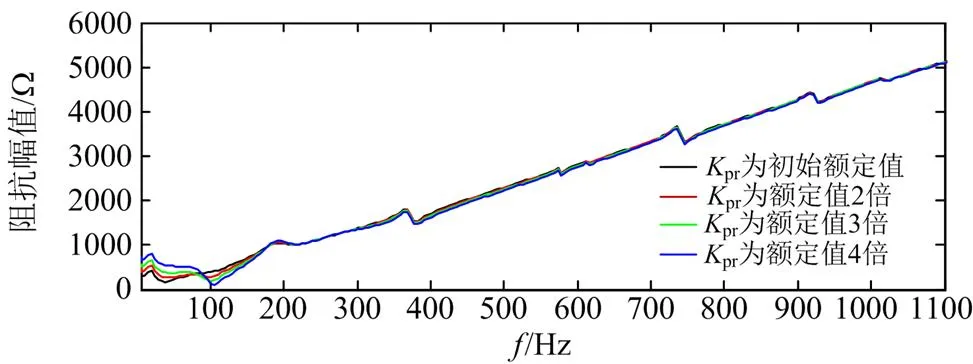
图11 整流侧平抗处直流阻抗跟整流站控制参数Kir的关系

2) 逆变站控制参数对整流侧直流谐波阻抗的影响

逆变侧控制系统参数pi和ii从额定值增大时，整流侧平抗处直流谐波阻抗的曲线变化情况如图12和图13所示。

图12 整流侧平抗处直流阻抗跟逆变站控制参数Kpi的关系

图13 整流侧平抗处直流阻抗跟逆变站控制参数Kii的关系

由图12和图13可见，逆变侧控制系统参数对整流侧平抗出口谐波阻抗也有一定影响，当pi和ii增大时，谐波阻抗频谱的原谐振点处阻抗变化不大，但当参数增大时，阻抗频谱低频段呈现两段相反的变化特性，一段频谱的阻抗增加，另一段频谱的阻抗减小，且逐渐开始产生新的谐振点，所以虽然逆变侧控制系统跟整流侧分处两个较远的换流站内，但逆变侧控制参数对整流侧平抗处谐波阻抗也有较大影响，在进行逆变站控制参数设计时也需考虑其对整个直流回路谐波阻抗的影响。

4.2.3两站交流系统参数的影响

4.2.3.1两站交流电源参数的影响

整流侧交流电源电感sr增加时，整流侧平抗处直流阻抗曲线如图14所示。

图14 整流侧平抗处直流阻抗跟整流侧交流电网电感Lsr的关系

4.2.3.2两站交流滤波器参数的影响

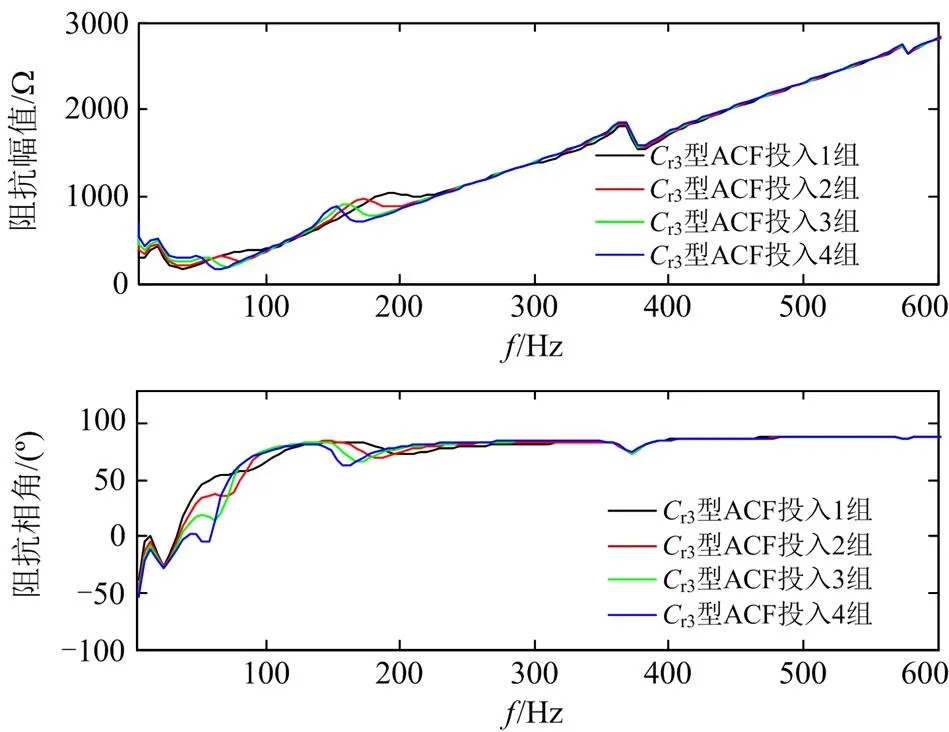
图15 整流侧平抗处直流阻抗跟整流侧Cr3型交流滤波器组数的关系

逆变侧投入的i3型滤波器组数增加时，整流侧平抗处直流阻抗100 Hz以上的部分不受影响，50 Hz以内阻抗各频段呈现不同的变化趋势，但改变幅度均较小，可忽略其影响，但谐振频率随组数增加而减小。

5 直流谐振抑制及仿真验证

由上面分析可知，高压直流系统的直流回路阻抗与交直流一二次系统参数均有关，其中控制参数的影响较为显著，且控制参数便于调整，所以本节研究以调整控制参数的方法来实现直流谐振的抑制，并进行仿真验证。

图16 整流侧故障(整流站单阀丢脉冲)时电流Idc与Kpr的关系

由图16可见，pr增加时，直流电流超调减小，总谐波含量减小，下面是pr增加时，故障电流的FFT分析结果对比情况。

由表2和图17可知，pr增加时，50 Hz附近的谐波电流逐渐减小，如图17中红色箭头所示，而100 Hz附近的谐波电流逐渐增加，如图中蓝色箭头所示，表明pr增加时，50 Hz附近谐波阻抗增加，100 Hz附近谐波阻抗减小，与图10的阻抗曲线结果一致，即增加pr可实现对50 Hz谐振抑制，减小pr可实现对100 Hz的谐振抑制，证明了本文所提方法的可行性。

表2 Kpr取不同值时整流侧故障电流典型谐波含量表

图17 Kpr取不同值时整流侧故障(整流站单阀丢脉冲)电流Idc典型谐波频谱

6 总结

1) 建立了典型高压直流输电系统的直流回路谐波阻抗解析计算模型，考虑了交流电网、交流滤波器、换流器开关、控制系统，直流滤波器和直流线路等各环节参数与直流谐波阻抗的耦合关系，适用于典型高压直流系统的直流谐波阻抗计算和谐振分析。

2) 分析了谐波源位置对直流回路谐波阻抗的影响，发现高压直流系统参数不变时，直流回路中不同位置处的谐波阻抗曲线和谐振特性不一，需根据谐振发生的位置进行针对性的分析和设计。

3) 分析了直流回路参数、两站控制系统参数和两站交流系统参等系统参数对直流回路谐波阻抗的影响。其中，控制系统参数的影响较为显著，其影响特性如下：(1) 控制系统的延时环节时间越长，谐振失稳风险越大，需尽量降低控制系统链路的延时环节总时长；(2) 控制系统各PI参数对直流谐波阻抗的影响主要表现在低频区域，且并不是全域单调相关，不同频带呈现不同的相关特性，需根据敏感频带不同做差异化设计。

4) 分析了远端逆变站参数对整流侧附近直流回路谐波阻抗的影响，发现直流回路阻抗与两站系统参数均有较明显关系，并不能仅因为两站相隔长距离线路就忽略对站系统参数的影响，需进行统一综合考虑。

5) 提出了基于控制参数调制的直流回路谐振的宽频抑制方法，并通过电磁暂态仿真验证了所提方法的可行性。提升了高压直流系统的直流谐振抑制的灵活性，进一步提升了高压直流系统的整体安全稳定运行能力。

附录A

1) 整流侧交流系统状态空间方程

根据第二章描述，图3中整流侧交流电网和交流滤波器的状态空间方程为

2) 逆变侧交流系统状态空间方程

根据第二章描述，图3中逆变侧交流电网和交流滤波器的状态空间方程为

[1] ONI O E, DAVIDSON I E, MBANGULA K N I. A review of LCC-HVDC and VSC-HVDC technologies and applications[J]. Transactions on Environment and Electrical Engineering, 2016, 1(3): 1-10.

[2] 朱金涛, 辛业春. 柔性高压直流输电仿真技术研究方法综述[J]. 智慧电力, 2021, 49(3): 1-11.

ZHU Jintao, XIN Yechun. Review of research on simulation methods of VSC-HVDC transmission system[J]. Smart Power, 2021, 49(3): 1-11.

[3] 李阳, 李骥, 郭纯海, 等. 基于谱峭度解卷积的特高压直流输电换流阀空冷器故障诊断方法[J]. 电网与清洁能源, 2021, 37(8): 48-52, 61.

LI Yang, LI Ji, GUO Chunhai, et al. Fault diagnosis method of converter valve air cooler based on spectral kurtosis deconvolution[J]. Power System and Clean Energy, 2021, 37(8): 48-52, 61.

[4] 娄彦涛, 袁妮, 刘琦. 高压直流输电晶闸管换流阀损耗仿真计算方法研究[J]. 高压电器, 2021, 57(1): 116-122, 128.

LOU Yantao, YUAN Ni, LIU Qi. Study on simulation calculation method of power losses for HVDC thyristor valve[J]. High Voltage Apparatus, 2021, 57(1): 116-122, 128.

[5] 赵东元, 胡楠, 傅靖, 等. 提升新能源电力系统灵活性的中国实践及发展路径研究[J]. 电力系统保护与控制, 2020, 48(24): 1-8.

ZHAO Dongyuan, HU Nan, FU Jing, et al. Research on the practice and road map of enhancing the flexibility of a new generation power system in China[J]. Power System Protection and Control, 2020, 48(24): 1-8.

[6] 汤广福, 庞辉, 贺之渊. 先进交直流输电技术在中国的发展与应用[J]. 中国电机工程学报, 2016, 36(7): 1760-1771.

TANG Guangfu, PANG Hui, HE Zhiyuan. R & D and application of advanced power transmission technology in China[J]. Proceedings of the CSEE, 2016, 36(7): 1760-1771.

[7] 饶宏, 冷祥彪, 潘雅娴, 等. 全球直流输电发展分析及国际化拓展建议[J]. 南方电网技术, 2019, 13(10): 1-7.

RAO Hong, LENG Xiangbiao, PAN Yaxian, et al. Analysis of the global HVDC power transmission development and the suggestion of the HVDC export[J]. Southern Power System Technology, 2019, 13(10): 1-7.

[8] 刘凤全, 王成福, 王瑞琪, 等. 含HVDC与P2G的跨区域电-气互联系统优化调度[J]. 电力建设, 2020, 41(12): 55-65.

LIU Fengquan, WANG Chengfu, WANG Ruiqi, et al. Optimal dispatch of cross-regional integrated electricity- gas system with HVDC and P2G[J]. Electric Power Construction, 2020, 41(12): 55-65.

[9] 谢永涛, 李希哲, 傅康, 等. ±800 kV特高压直流输电工程技术[J]. 西北水电, 2019(2): 70-74.

XIE Yongtao, LI Xizhe, FU Kang, et al. ±800 kV UHVDC transmission engineering technology[J]. Northwest Hydropower, 2019(2): 70-74.

[10] 谷琛, 李鹏, 何慧雯, 等. ±1100 kV以上电压等级直流输电技术研究[J]. 中国电机工程学报, 2020, 40(20): 6745-6754.

GU Chen, LI Peng, HE Huiwen, et al. Research on ±1100 kV and above UHV DC transmission technologies[J]. Proceedings of the CSEE, 2020, 40(20): 6745-6754.

[11] 李鹏, 谷琛, 陈东, 等. ±1500 kV特高压直流输电技术前期研究[J]. 高电压技术, 2017, 43(10): 3139-3148.

LI Peng, GU Chen, CHEN Dong, et al. Development of technologies in ±1 500 kV UHV DC transmission research[J]. High Voltage Engineering, 2017, 43(10): 3139-3148.

[12] 张国辉, 景柳铭, 王宾, 等. 谐波引起的高压直流输电连续换相失败抑制方法研究[J]. 电力系统保护与控制, 2020, 48(5): 33-41.

ZHANG Guohui, JING Liuming, WANG Bin, et al. Study on HVDC consecutive commutation failures mitigation method caused by harmonics[J]. Power System Protection and Control, 2020, 48(5): 33-41.

[13] 朱大鹏, 许斌, 曾静. 向家坝—上海特高压直流输电工程直流回路的谐振研究[J]. 电力建设, 2008, 29(5): 1-4.

ZHU Dapeng, XU Bin, ZENG Jing. Study on DC circuit resonance of Xiangjiaba-Shanghai UHVDC transmission line[J]. Electric Power Construction, 2008, 29(5): 1-4.

[14] 马俊民, 黄永瑞, 何青连. ±800 kV特高压直流输电系统谐波研究[J]. 电力系统保护与控制, 2013, 41(21): 33-37.

MA Junmin, HUANG Yongrui, HE Qinglian. Research on harmonics of ±800 kV ultra high voltage direct current transmission system[J]. Power System Protection and Control, 2013, 41(21): 33-37.

[15] 丁扬, 种芝艺, 黄杰, 等. 高压直流输电工程谐振研究[J]. 电网技术, 2012, 36(12): 189-194.

DING Yang, CHONG Zhiyi, HUANG Jie, et al. Study on DC resonance in HVDC power transmission projects[J]. Power System Technology, 2012, 36(12): 189-194.

[16] 侯婷, 王国强, 郭龙, 等. 混合高压直流输电系统的直流谐振抑制方法[J]. 南方电网技术, 2019, 13(8): 9-14.

HOU Ting, WANG Guoqiang, GUO Long, et al. DC resonance suppression method for hybrid HVDC transmission system[J]. Southern Power System Technology, 2019, 13(8): 9-14.

[17] 王俊茜, 贾祺, 刘侃, 等. 基于信号注入法的风火打捆经直流外送系统次同步扭振分析[J]. 电力系统保护与控制, 2021, 49(17): 109-120.

WANG Junxi, JIA Qi, LIU Kan, et al. Analysis of sub-synchronous torsional mode of wind-thermal bundled system transmitted via HVDC based on a signal injection method[J]. Power System Protection and Control, 2021, 49(17): 109-120.

[18] MUNIAPPAN M. A comprehensive review of DC fault protection methods in HVDC transmission systems[J]. Protection and Control of Modern Power Systems, 2021, 6(1): 1-20.

[19] 徐政, 裘鹏, 黄莹, 等. 采用时域仿真的高压直流输电直流回路谐振特性分析[J]. 高电压技术, 2010, 36(1): 44-53.

XU Zheng, QIU Peng, HUANG Ying, et al. HVDC system DC loop resonance analysis using time domain simulation[J]. High Voltage Engineering, 2010, 36(1): 44-53.

[20] 邓晶, 赵晓斌, 黄莹, 等. 基于PSCAD/EMTDC的高压直流回路谐振研究[J]. 南方电网技术, 2014, 8(6): 53-57.

DENG Jing, ZHAO Xiaobin, HUANG Ying, et al. Study on HVDC system DC loop resonance based on PSCAD/EMTDC[J]. Southern Power System Technology, 2014, 8(6): 53-57.

[21] 李清, 周强, 张东辉, 等. 基于测试信号法的HVDC谐波阻抗扫描方法研究[J]. 电力系统保护与控制, 2021, 49(14): 168-175.

LI Qing, ZHOU Qiang, ZHANG Donghui, et al. An harmonic impedance scanning method of HVDC based on a test signal method[J]. Power System Protection and Control, 2021, 49(14): 168-175.

[22] 徐攀腾, 朱博, 喻文翔, 等. 昆柳龙直流工程受端高频谐振评估及抑制[J]. 中国电力, 2022, 55(3): 9-17.

XU Panteng, ZHU Bo, YU Wenxiang, et al. High- frequency resonance evaluation and suppression measures for receiving-end of Kun-Liu-Long DC project[J]. Electric Power, 2022, 55(3): 9-17.

[23] 王彤彤, 文俊, 靳海强, 等. LCC-MMC混合直流输电系统直流回路谐振特性研究[J]. 电网与清洁能源, 2021, 37(3): 1-7.

WANG Tongtong, WEN Jun, JIN Haiqiang, et al. Research on the resonance characteristics of the DC loop of the LCC-MMC hybrid DC transmission system[J]. Power System and Clean Energy, 2021, 37(3): 1-7.

[24] ZHANG Z, XU Z, XUE Y, et al. DC-side harmonic currents calculation and DC-loop resonance analysis for an LCC-MMC hybrid HVDC transmission system[J]. IEEE Transactions on Power Delivery, 2015, 30(2): 642-651.

[25] 马玉龙, 肖湘宁, 姜旭, 等. HVDC换流器的阻抗频率特性[J]. 电力系统自动化, 2006, 30(12): 66-69, 91.

MA Yulong, XIAO Xiangning, JIANG Xu, et al. Study on impedance-frequency characteristic of HVDC converter[J]. Automation of Electric Power Systems, 2006, 30(12): 66-69, 91.

[26] 王钢, 李志铿, 李海锋, 等. HVDC换流器等值谐波阻抗的计算方法[J]. 中国电机工程学报, 2010, 30(19): 64-68.

WANG Gang, LI Zhikeng, LI Haifeng, et al. Calculation method of harmonic equivalent impedances of HVDC converter[J]. Proceedings of the CSEE, 2010, 30(19): 64-68.

[27] LIU H, JIAN S. DC terminal impedance modeling of LCC-based HVDC converters[C] // 2013 IEEE 14th Workshop on Control and Modeling for Power Electronics (COMPEL), June 23-26, 2013, Salt Lake City, UT, USA: 1-8.

[28] 郭贤珊, 马为民. 向家坝—上海±800 kV特高压直流示范工程的低频谐振分析[J]. 电网技术, 2008, 32(10): 1-4.

GUO Xianshan, MA Weimin. Analysis on low frequency resonance in ±800 kV UHVDC demonstration project from Xiangjiaba to Shanghai[J]. Power System Technology, 2008, 32(10): 1-4.

[29] 任军辉, 张帆, 杨晓平. 滇西北至广东特高压直流输电工程直流回路的谐振研究[J]. 电力电容器与无功补偿, 2018, 39(6): 29-32.

REN Junhui, ZHANG Fan, YANG Xiaoping. Study on resonance of DC circuit for Dianxibei to Guangdong UHVDC project[J]. Power Capacitor & Reactive Power Compensation, 2018, 39(6): 29-32.

[30] 孙正, 李可军, 王宇红, 等. HVDC直流有源滤波器容量的影响因素分析及其改进方法[J]. 电力自动化设备, 2012, 32(11): 111-114.

SUN Zheng, LI Kejun, WANG Yuhong, et al. Analysis of affecting factors on capacity of DC active power filter for HVDC system and improvement[J]. Electric Power Automation Equipment, 2012, 32(11): 111-114.

[31] 杜夏冰, 赵成勇, 吴方劼, 等. LCC-HVDC系统混合型有源滤波器谐振抑制策略[J]. 电力系统自动化, 2021, 45(4): 115-122.

DU Xiabing, ZHAO Chengyong, WU Fangjie, et al. Resonance suppression strategy of hybrid active power filter in LCC-HVDC system[J]. Automation of Electric Power Systems, 2021, 45(4): 115-122.

[32] ZHANG W, ASPLUND G, ABERG A, et al. Active DC filter for HVDC system-a test installation in the Konti-Skan DC link at Lindome converter station[J]. IEEE Transactions on Power Delivery, 1993, 8(3): 1599-1606.

[33] ZHANG W, ISAKSSON A J, EKSTROM A. Analysis on the control principle of the active DC filter in the Lindome converter station of the Konti-Skan HVDC link[J]. IEEE Transactions on Power Systems, 1998, 13(2): 374-381.

[34] HAO P, ZANJI W, JIANYE C. Study on the control of shunt active DC filter for HVDC systems[J]. IEEE Transactions on Power Delivery, 2008, 23(1): 396-401.

[35] HAJIBEIGY M, FARSADI M, NAZARPOUR D, et al. Harmonic suppression in HVDC system using a modified control method for hybrid active DC filter[J]. European Transactions on Electrical Power, 2012, 22(3): 294-307.

[36] 常怡然, 吴方劼, 何师, 等. 应用在高压直流输电系统中的混合型有源滤波器稳定性分析及控制方法[J]. 电力系统及其自动化学报, 2021, 33(2): 75-82.

CHANG Yiran, WU Fangjie, HE Shi, et al. Stability analysis and control method for hybrid active power filter applied to HVDC system[J]. Proceedings of the CSU-EPSA, 2021, 33(2): 75-82.

[37] 李云丰, 汤广福, 吴亚楠, 等. 直流电网建模分析与阻尼控制研究[J]. 中国电机工程学报, 2017, 37(12): 3372-3382, 3664.

LI Yunfeng, TANG Guangfu, WU Yanan, et al. Modeling, analysis and damping control of DC grid[J]. Proceedings of the CSEE, 2017, 37(12): 3372-3382, 3664.

Analytical calculation of DC harmonic impedance and DC resonance analysis of an HVDC transmission system

LI Huan, FU Chuang, XIN Qingming, DAI Shulong, ZHAO Xiaobin

(State Key Laboratory of HVDC, CSG Electrical Power Research Institute, Guangzhou 510663, China)

In this paper, the DC loop harmonic resonance of a conventional HVDC system is studied. An analytic calculation method is used to establish the mathematical model of the DC loop harmonic impedance of an LCC HVDC system. Based on the state-space model, an analytical expression of the DC harmonic impedance is derived. The DC loop impedance spectrum is then formed and verified by PSCAD simulation. The coupling relationship between the HVDC parameters and the DC harmonic impedance is analyzed. Finally, a method to suppress broadband resonance of the DC loop by adjusting control parameters is proposed and verified by electromagnetic transient simulation. The results show that the proposed method can effectively suppress the DC resonance of the HVDC system and ensure the secure and stable operation of the system.

high voltage direct current; direct current harmonic impedance; analytical calculation; resonance analysis

10.19783/j.cnki.pspc.211629

国家自然科学基金项目资助(51777079)；南方电网科技项目资助(ZBKJXM20190056)

This work is supported by the National Natural Science Foundation of China (No. 51777079).

2021-12-01；

2022-06-07

李 欢(1986—)，男，博士研究生，研究方向为高压直流输电及大功率电力电子技术；E-mail: 270660445@qq.com

傅 闯(1973—)，男，教授级高级工程师，研究方向为大功率电力电子、高压直流输电、电能质量控制。E-mail: fuchuang@csg.cn

(编辑 周金梅)