集成自适应啁啾模态分解和BiLSTM的短期负荷组合预测模型
姚浩然,李成鑫,郑秀娟,杨 平
集成自适应啁啾模态分解和BiLSTM的短期负荷组合预测模型
姚浩然,李成鑫,郑秀娟,杨 平
(四川大学电气工程学院,四川 成都 610065)
为提高用户侧短期负荷预测的精度,提出了一种基于自适应啁啾模态分解(adaptive chirp mode decomposition, ACMD)和麻雀搜索算法(sparrow search algorithm, SSA)优化双向长短时记忆网络(bi-directional long short-term memory, BiLSTM)的短期负荷组合预测方法。针对短期电力负荷存在波动性强和非平稳性的问题,采用ACMD将短期负荷时间序列分解为多个相对简单的子分量,使用BiLSTM分别对各子分量进行预测。同时,为克服BiLSTM参数取值不同导致预测结果不稳定的问题,使用SSA优化BiLSTM模型的超参数。最后将各子分量预测结果叠加得到最终预测结果。通过具体算例,分别与单一预测模型和多种组合预测模型进行比较,实验结果表明该方法具有更高的预测精度。
负荷预测;双向长短时记忆网络;自适应啁啾模态分解;麻雀搜索算法;时序分解
0 引言
负荷预测是电网安全经济运行的前提,也是制定电力供应计划和电力调度的重要依据[1]。随着用户侧分布式电源发展和高比例新能源的并网,负荷的波动性和随机性大大增强,这给负荷预测工作带来很大挑战[2-3]。当前无论是发电侧还是售电侧都对负荷预测的准确度提出了更高的要求,预测误差的减少能显著提升电网运行的经济效益和社会效益[4]。相较于区域级负荷预测对于发电部门和电力调度部门的参考和指导作用而言,企业级负荷预测的侧重点在于帮助企业级用户和电力供应部门实现无缝对接和双向沟通[5-6]。对企业级用户而言,可以通过负荷预测了解自身用电习惯并为制定合理的购电计划提供依据[7];对供电公司而言,可以帮助供电公司实现对企业用户的用电监控;对于售电公司而言,当前客户多为企业级客户,售电公司需要对其所代理用户的负荷进行准确预测,负荷预测的结果是售电公司制定购售电计划的重要依据[8-9]。因此,在电力市场化进程不断加快的背景下,提高用户侧负荷预测的精度非常必要。
目前,有关负荷预测的方法可分为三类。第一类是以线性回归[10]、ARIMA[11]和指数平滑[12-13]为代表的传统预测方法。传统方法虽然结构简单易于实施,但在非线性时序预测问题方面表现很差。第二类是以机器学习和深度学习为代表的人工智能方法,此类方法提高了对非线性问题的处理能力。近几年随着计算机计算能力的提升,以神经网络为代表的深度学习模型[14]广泛应用于负荷预测领域。已有学者使用人工神经网络[15]、深度置信网络[16]和长短时记忆网络(long short term memory, LSTM)[17-19]进行负荷预测,均取得了不错的效果,其中LSTM在时序预测中的应用最为广泛。然而此类方法也存在收敛慢、参数调节繁琐和稳定性不佳等问题。第三类是组合预测法,组合预测法被设计为集成多个模型,可充分利用各模型的优势来克服单一预测方法的局限性。
组合预测法的常见思路分为两种。第一种思路是将启发式优化算法与单个预测模型进行组合,对模型的超参数取值进行选择和设置[20]。文献[21]使用粒子群算法对深度置信网络模型进行优化;文献[22]提出了基于遗传算法优化BP神经网络的预测模型;较单一模型而言,均提高了预测的精度。第二种思路是结合信息领域的信号分解技术,对时序数据进行预处理来降低数据的复杂度,再进行预测。文献[23]提出了一种基于经验模式分解(empirical mode decomposition, EMD)和LSTM组合的短期负荷预测模型,与单一LSTM模型相比,预测精度更高。文献[24-25]将变分模态分解(variational mode decomposition, VMD)和LSTM相结合,降低了预测误差。然而,EMD存在模态混叠问题,会影响预测的精度;VMD要提前设置分解后模态个数,在实际工程应用中需反复试验,非常不便。文献[26]提出了一种新的非平稳信号分解算法——自适应啁啾模态分解(adaptive chirp mode decomposition, ACMD),与其他方法相比,ACMD抗噪性强且无需预置分解模式的数量,在处理具有强时变特性的多模信号时具有明显优势。
鉴于此,本文将ACMD用于负荷预测领域,提出了一种基于ACMD和双向长短时记忆网络[27](bi-directional long short-term memory, BiLSTM)的短期负荷组合预测方法。使用ACMD将时序负荷序列分解成多个相对简单的子序列,对每个子序列分别建立BiLSTM预测模型,并使用一种新型启发式算法——麻雀搜索算法[28](sparrow search algorithm, SSA)对BiLSTM的超参数进行寻优,将各子序列预测结果叠加得到最终预测结果。通过实际算例,与EMD进行对比分析,验证了本文所提组合预测方法能有效提高预测精度。
1 短期电力负荷组合预测模型
基于ACMD和SSA-BiLSTM的短期电力负荷组合预测模型架构如图1所示,主要步骤如下。

图1 基于ACMD-SSA-BiLSTM的短期负荷组合预测模型
1) 使用ACMD方法对历史负荷序列数据进行分解,得出个子序列。
2) 结合相关特征,对分解后得到的个子序列分别构建BiLSTM预测模型。
3) 对构建的个BiLSTM模型超参数采用SSA优化,根据优化后的超参数值构建最优预测模型。
4) 将各子序列预测结果进行叠加组合得到最终的预测结果,并对比其他预测方法,通过相关评价指标对预测结果进行评估,分析模型的预测效果。
2 基于ACMD的负荷时间序列分解
电力负荷受生产生活、气象、经济等因素的影响,呈现出一定的波动性和非平稳性特点。但由于电力用户的电力消费习惯有一定的规律性,因此,电力负荷也具有明显的周期波动趋势。若算法能较好地捕捉到负荷的周期性规律,将有助于有效提升负荷预测的精准度。本文通过ACMD算法对原始非平稳序列进行分解,ACMD是一种自适应信号分解算法,采用递归算法的框架匹配追踪,可以有效处理具有强时变特性的多模信号[26]。
使用ACMD处理负荷预测所需的历史功率信号,可表示为
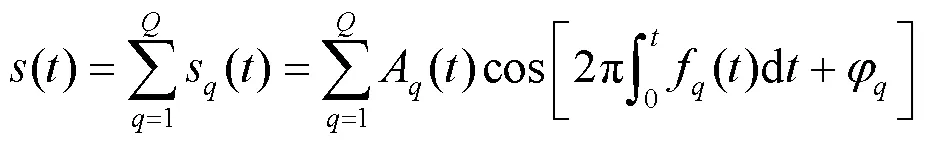
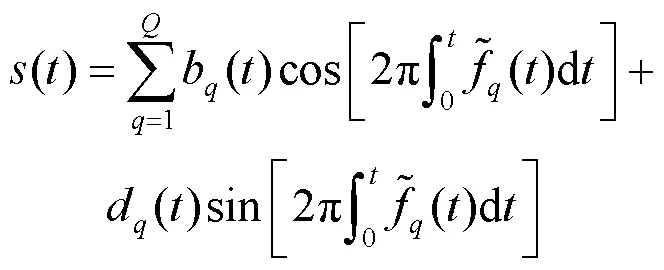



通过交替更新解调信号和频率函数来求解此优化问题,实现对原始信号的逐个分解,在得到第1个信号分量之后,将其从原始信号中减去,然后将剩余分量作为新的初始信号继续分解得到第2个信号分量,反复循环更新,直到获取全部信号分量。
3 SSA-BiLSTM
3.1 BiLSTM原理
LSTM基于循环神经网络设计而成,作为一种特殊的循环神经网络,LSTM增加了门控机制,可以有效抑制训练过程出现的梯度消失问题,被广泛应用于预测问题中,尤其适用于时序数据的预测。其具体结构如图2所示。

图2 LSTM结构图

LSTM只能编码时间序列从前到后的信息,无法对从后到前的信息进行编码。本文选用BiLSTM进行预测,其结构如图3所示。BiLSTM采用两层LSTM组合而成,同时考虑前向和反向两个方向的序列[27]。其中前向层用于捕捉当前时间节点之前的特征序列,反向层用于捕捉未来时刻到当前时间节点的特征序列。通过前后两层的组合,其预测结果通常优于LSTM。
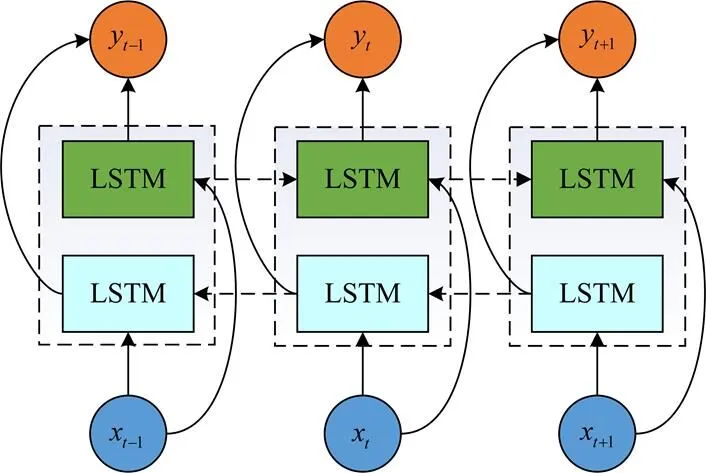
图3 BiLSTM结构图
3.2 SSA原理
SSA启发于麻雀的觅食行为[28],与粒子群和遗传算法相比,具有速度快、精度高和参数少等优点,有很强的工程应用潜力[29]。麻雀群在觅食的过程中分工明确,有寻找优质食物的发现者和尾随其后的加入者。与传统的发现-跟随者模型不同的是,麻雀算法增加了侦察预警机制,选取种群中一定比例的麻雀作为报警者,警惕攻击和夺食行为,发现危险则放弃当前食物。通过在维解空间内不断更新各类麻雀的位置,比较适应度值来寻求更好的位置,即求解目标函数的最优解。
其中发现者的位置更新如式(7)。


每代种群都会抽取一定比例的个体为报警者,报警者更新描述为
3.3 SSA-BiLSTM负荷预测模型
BiLSTM算法存在一些超参数,在使用BiLSTM对电力负荷进行预测时,超参数的取值不同会对模型的预测精度产生很大影响。根据经验手动调整参数费时费力,且不确定性强。因此为了提升预测的精度,使用SSA强大的寻优能力对BiLSTM各超参数的取值进行快速精准的确定。本文选取对BiLSTM影响较大的3个超参数为优化对象,分别为学习率(learning_rate)、第一层隐藏层单元数(numHiddenUnits1)和第二层隐藏层单元数(numHiddenUnits2)。使用均方误差函数(mean square error, MSE)作为适应度函数。SSA的目标是找到使得BiLSTM训练样本MSE最小的一组超参数组合。MSE表示预测功率与实际功率的差异程度,可表示为
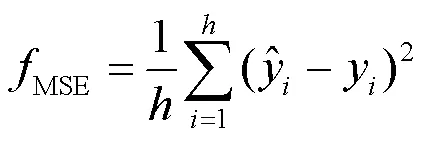
图4为SSA-BiLSTM预测模型流程,其主要步骤如下。
1) 设置SSA的麻雀种群数目、不同任务分工麻雀所占比例以及最大迭代次数;
2) 在解空间里初始化待优化参数;
3) 使用对应的参数值构建BiLSTM模型对样本进行训练,并计算适应度值;
4) 根据BiLSTM传出的适应度值更新麻雀种群位置,得到新的解,将对应解(参数取值)传给BiLSTM进行训练;
5) 重复步骤2)和步骤3),直至迭代完成;
6) 输出最优参数值组合,建立最优BiLSTM预测模型。
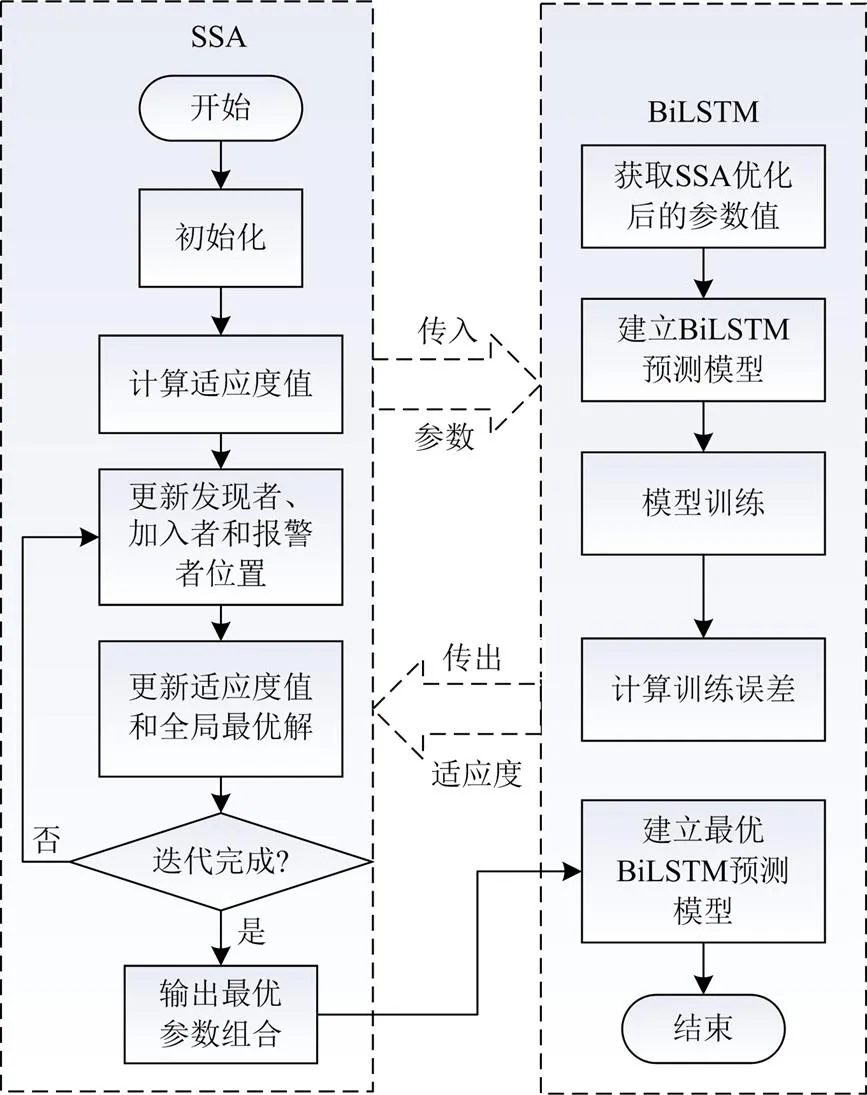
图4 SSA优化BiLSTM流程图
4 算例分析
实验所用计算机处理器为Intel Core i5-7500 CPU@3.40 GHz,运行内存为12 GB,GPU为GeForce GT710。基于Matlab2020a及Deep Learning Toolbox环境进行编程。实验采用广东省某企业2017年7月1日至8月20日的负荷数据,采样间隔为15 min。原始数据划分为80%的训练数据和20%的测试数据。
4.1 评价指标
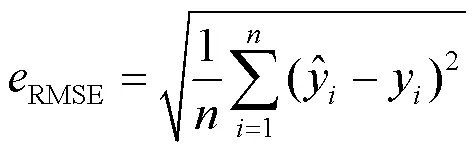
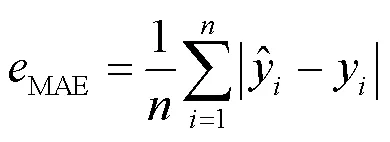

4.2 ACMD-BiLSTM有效性验证
为验证ACMD的有效性,对原始负荷训练数据分别采取:(1) 不作分解直接预测;(2) 使用EMD分解后再预测;(3) 使用ACMD分解后再预测。对分解后的每一组子序列分别使用BiLSTM模型进行预测,将各序列预测结果进行叠加,得到三种方法的最终负荷预测结果。
4.2.1 ACMD和EMD分解效果对比
为比较ACMD和EMD的分解效果,在训练数据中选取1500个样本点,分别使用EMD和ACMD进行分解,分解结果分别如图5和图6所示。其中纵坐标表示各采集样点的原始负荷分解后各子序列的负荷,单位为kW。
从图5和图6可以看出,原始负荷序列具有较强的波动性和非平稳性。从分解后子序列数量上来看,EMD分解后产生了9个子序列,而ACMD分解后的子序列只有6个,可以有效地减少后续对各子序列分别建立预测模型的计算量。比较两种方法分解结果的高频部分可以发现,EMD高频分量较为杂乱,规律性差,而ACMD高频分量规律性较强,存在一定的周期性。对比低频分量可以发现,二者低频分量都有较大的幅值,趋势平缓,但ACMD低频趋势与原序列更接近。综合分析可知,ACMD分解后的各子序列更有利于后续预测建模。

图5 EMD算法分解结果
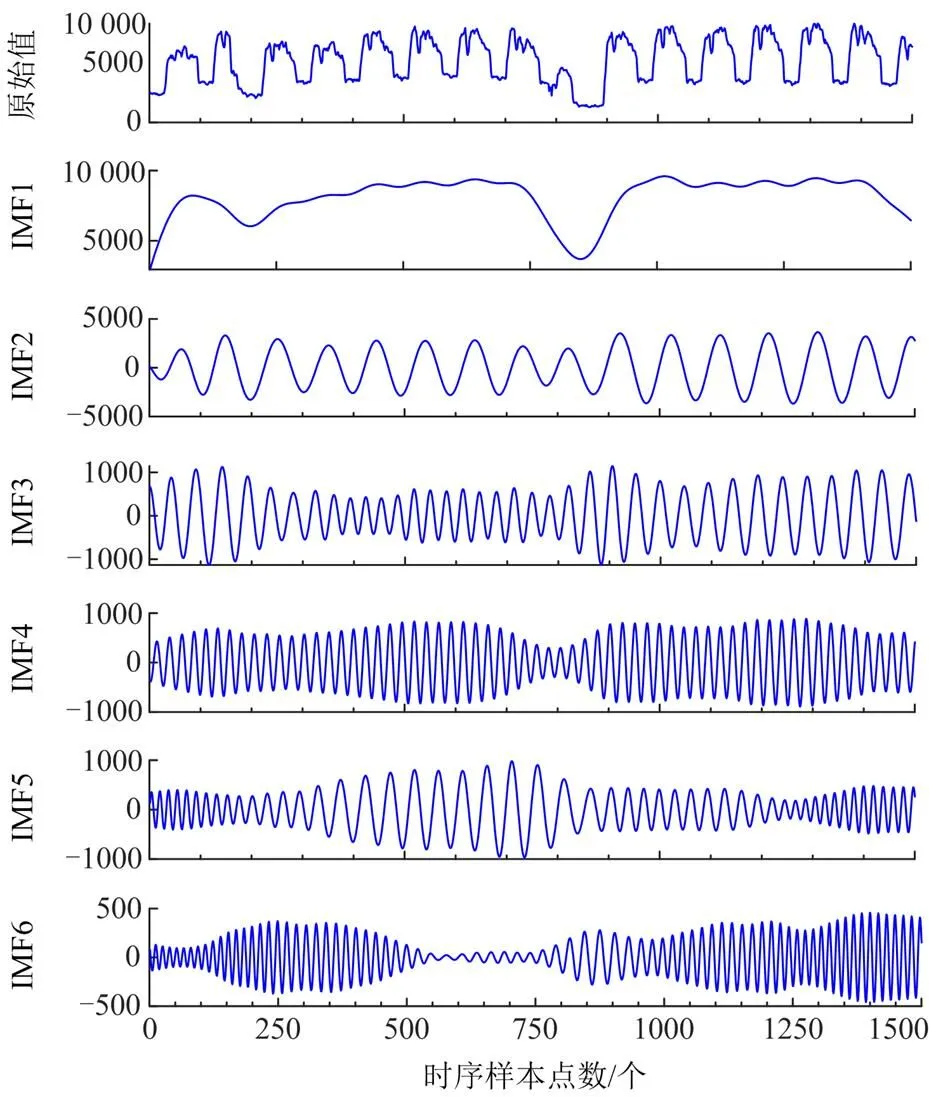
图6 ACMD算法分解结果
4.2.2 ACMD-BiLSTM预测结果
对不作分解、采用EMD分解以及采用ACMD分解的数据都采取BiLSTM进行预测建模,各方法的预测误差如图7所示,评价指标如表1所示。
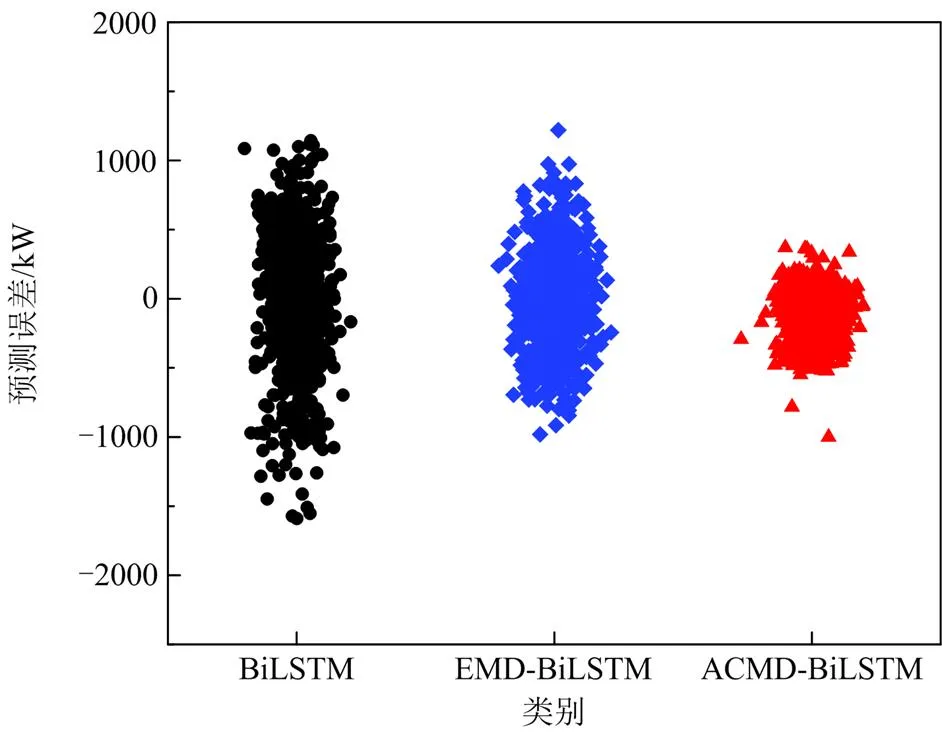
图7 使用不同分解方法的预测误差分布图

表1 使用不同分解方法的评价指标
从图7和表1可以得出以下结论。
1) 相比于不作分解直接使用原数据进行预测的BiLSTM模型,EMD-BiLSTM和ACMD-BiLSTM预测误差更小且误差分布更集中,RMSE分别减少了132.33 kW和232.49 kW,MAE分别减少了56.85%和136.47%,MAPE分别降低了0.55%和1.86%。可以发现,通过分解再预测的方法,可以提升模型的预测效果。
2) 与EMD-BiLSTM模型相比,ACMD-BiLSTM预测误差分布集中于原点附近,预测误差更小,各评价指标值也更优。表明ACMD分解后的子序列趋势性更强,更有利于预测精度的提升。
4.3 SSA有效性验证
为验证SSA-BiLSTM模型的有效性,对原始数据分别采用:(1) BiLSTM模型直接进行预测;(2) SSA优化BiLSTM模型进行预测。BiLSTM最大训练次数(Epochs)设置为100次,选用Adam优化器。SSA参数设置如下:种群麻雀总数为30,种群中发现、加入、警戒者的比例为7:2:1,最大迭代次数为30次。BiLSTM中3个待优化参数的优化区间:learning_rate为[0.001, 0.1];numHiddenUnits1和numHiddenUnits2为[1, 100]。
SSA优化过程中适应度变化曲线如图8所示。适应度值为实际功率与预测功率的差值,单位为kW。可以发现,经过12次迭代后,SSA趋于收敛。最终得到优化后的参数取值:learning_rate为0.0069,numHiddenUnits1为48,numHiddenUnits2为37。

图8 SSA适应度曲线
BiLSTM和SSA-BiLSTM的预测结果和评价指标分别如图9和表2所示。由图9和表2可以得出:
1) SSA-BiLSTM模型各项评价指标均优于BiLSTM模型,说明其预测效果更好。
2) 与BiLSTM模型的预测曲线相比,SSA- BiLSTM模型的预测曲线与真实负荷曲线更接近,尤其是在负荷波峰和波谷处,验证了SSA的有效性。

图9 SSA优化前后预测曲线对比

表2 SSA优化前后模型性能对比
4.4 ACMD-SSA-BiLSTM预测结果分析
上文分别验证了ACMD和SSA的有效性。本节继续验证ACMD、SSA、BiLSTM三者组合的预测效果,建立ACMD-SSA-BiLSTM组合预测模型。同时设置对比实验,预测模型分别采用:(1) LSTM;(2) BiLSTM;(3) EMD-BiLSTM;(4) ACMD-BiLSTM;(5) SSA-BiLSTM;(6) ACMD-SSA-BiLSTM。各方法的部分预测曲线和评价指标分别如图10和表3所示。
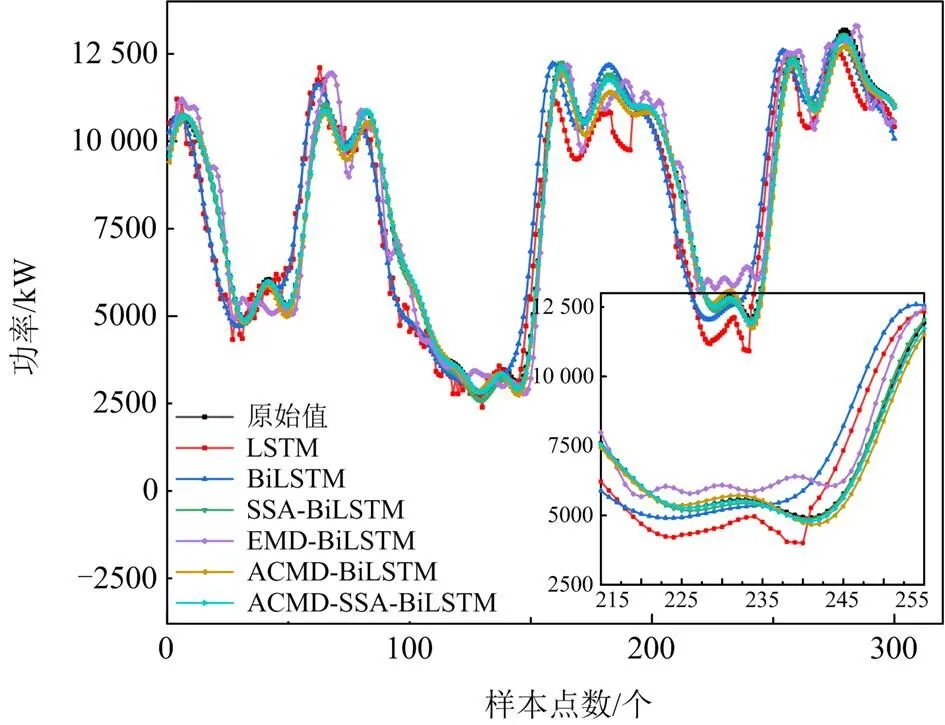
图10 各模型预测曲线对比

表3 各模型评价指标对比
通过对比表3和图10可以得出:
1) BiLSTM作为LSTM的改进模型,同时考虑负荷序列前向和反向两个方向,能够有效挖掘负荷序列前向和反向上的时序规律,BiLSTM相较于LSTM,RMSE、MAE分别降低了166.24 kW和48.22 kW,MAPE降低了0.699%,表现出了更强的时序学习能力。
2) 本文所提ACMD-SSA-BiLSTM组合预测模型相较于其他模型,预测曲线与真实负荷曲线贴近度最高,预测效果最好。相较于单一预测模型LSTM和BiLSTM,其RMSE分别下降了505.44 kW和339.2 kW,MAE分别下降了272.94 kW和224.72 kW,MAPE分别降低了3.644%和2.945%。相较于两两组合的预测模型EMD-BiLSTM、ACMD-BiLSTM和SSA-BiLSTM,RMSE分别降低了206.87 kW、106.71 kW和64.28 kW,MAE分别降低了167.87 kW、88.25 kW和55.43 kW,MAPE分别降低了2.839%、1.085%和0.33%。验证了ACMD-SSA- BiLSTM负荷预测模型的有效性。
5 结论
精准的企业级负荷预测是提高电力市场的交易效率和各方经济收益的重要保证。在智能算法快速发展和负荷预测精度要求不断提高的背景下,本文提出了一种基于ACMD-SSA-BiLSTM的短期负荷组合预测方法,得出以下结论。
1) 相比于传统EMD方法,ACMD方法对非线性信号分解效果更好,能够将原始负荷序列分解为一系列更为平稳、规律性更强的子序列,且分解后的子序列数量更少,减少预测工作量的同时提高了预测的准确率。
2)在BiLSTM预测过程中,引入SSA对BiLSTM的超参数进行寻优,克服了人工调节参数带来的高不确定性和效果不佳的缺点。
3) ACMD-SSA-BiLSTM组合预测模型,通过对原始序列分解而成的简单子序列分别预测并寻优,再将预测结果叠加得到最终结果。与单一模型及其他组合模型相比,预测效果更好、精度更高,具有一定的应用优势。
后续将结合注意力机制、残差网络等技术,充分挖掘更多可表征的预测特征,提高模型的特征提取能力。
[1] 王凌云, 林跃涵, 童华敏, 等. 基于改进Apriori关联分析及MFOLSTM算法的短期负荷预测[J]. 电力系统保护与控制, 2021, 49(20): 74-81.
WANG Lingyun, LIN Yuehan, TONG Huamin, et al. Short-term load forecasting based on improved Apriori correlation analysis and an MFOLSTM algorithm[J]. Power System Protection and Control, 2021, 49(20): 74-81.
[2] 刘友波, 吴浩, 刘挺坚, 等. 集成经验模态分解与深度学习的用户侧净负荷预测算法[J]. 电力系统自动化, 2021, 45(24): 57-64.
LIU Youbo, WU Hao, LIU Tingjian, et al. User-side net load forecasting method integrating empirical mode decomposition and deep learning[J]. Automation of Electric Power Systems, 2021, 45(24): 57-64.
[3] BOZORG M, BRACALE A, CARAMIA P, et al. Bayesian bootstrap quantile regression for probabilistic photovoltaic power forecasting[J]. Protection and Control of Modern Power Systems, 2020, 5(3): 218-229.
[4] ÜRGE-VORSATZ D, CABEZA L F, SERRANO S, et al. Heating and cooling energy trends and drivers in buildings[J]. Renewable and Sustainable Energy Reviews, 2015, 41: 85-98.
[5] WANG Y, KONG Y, TANG X, et al. Short-term industrial load forecasting based on ensemble hidden Markov model[J]. IEEE Access, 2020, 8: 160858-160870.
[6] KHURSHEED A, MUSAED A, KUMAIL J, et al. A pyramid-CNN based deep learning model for power load forecasting of similar-profile energy customers based on clustering[J]. IEEE Access, 2021, 9: 14992-15003.
[7] 杨德州, 刘嘉明, 宋汶秦, 等. 基于改进型自适应白噪声完备集成经验模态分解的工业用户负荷预测方法[J].电力系统保护与控制, 2022, 50(4): 36-43.
YANG Dezhou, LIU Jiaming, SONG Wenqin, et al. A load forecasting method for industrial customers based on the ICEEMDAN algorithm[J]. Power System Protection and Control, 2022, 50(4): 36-43.
[8] 彭文, 王金睿, 尹山青. 电力市场中基于Attention- LSTM的短期负荷预测模型[J]. 电网技术, 2019, 43(5): 1745-1751.
PENG Wen, WANG Jinrui, YIN Shanqing. Short-term load forecasting model based on Attention- LSTM in electricity market[J]. Power System Technology, 2019, 43(5): 1745-1751.
[9] 杨斌, 杨世海, 曹晓冬, 等. 基于EMD-QRF的用户负荷概率密度预测[J]. 电力系统保护与控制, 2019, 47(16): 1-7.
YANG Bin, YANG Shihai, CAO Xiaodong, et al. Short-term consumer load probability density forecasting based on EMD-QRF[J]. Power System Protection and Control, 2019, 47(16): 1-7.
[10] AMRAL N, OZVEREN C S, KING D. Short term load forecasting using multiple linear regression[C] // 2007 42nd International Universities Power Engineering Conference, September 4-6, 2007, Brighton, UK: 1192-1198.
[11] WANG Y, WANG J, ZHAO G, et al. Application of residual modification approach in seasonal ARIMA for electricity demand forecasting: a case study of China[J]. Energy Policy, 2012, 48: 284-294.
[12] TAYLOR J W. Short-term electricity demand forecasting using double seasonal exponential smoothing[J]. Journal of the Operational Research Society, 2003, 54(8): 799-805.
[13] CHRISTIAANSE W R. Short-term load forecasting using general exponential smoothing[J]. IEEE Transactions on Power Apparatus and Systems, 1971, 90(2): 900-911.
[14] TONG C, LI J, LANG C, et al. An efficient deep model for day-ahead electricity load forecasting with stacked denoising auto-encoders[J]. Journal of Parallel and Distributed Computing, 2018, 117: 267-273.
[15] HERNÁNDEZ L, BALADRÓN C, AGUIAR J M, et al. Artificial neural network for short-term load forecasting in distribution systems[J]. Energies, 2014, 7(3): 1576-1598.
[16] 杨智宇, 刘俊勇, 刘友波, 等. 基于自适应深度信念网络的变电站负荷预测[J]. 中国电机工程学报, 2019, 39(14): 4049-4061.
YANG Zhiyu, LIU Junyong, LIU Youbo, et al. Transformer load forecasting based on adaptive deep belief network[J]. Proceedings of the CSEE, 2019, 39(14): 4049-4061.
[17] 陈振宇, 刘金波, 李晨, 等. 基于LSTM与XGBoost组合模型的超短期电力负荷预测[J]. 电网技术, 2020, 44(2): 614-620.
CHEN Zhenyu, LIU Jinbo, LI Chen, et al. Ultra short-term power load forecasting based on combined LSTM-XGBoost model[J]. Power System Technology, 2020, 44(2): 614-620.
[18] WANG Y, GAN D, SUN M, et al. Probabilistic individual load forecasting using pinball loss guided LSTM[J]. Applied Energy, 2019, 235: 10-20.
[19] CIECHULSKI T, OSOWSKI S. High precision LSTM model for short-time load forecasting in power systems[J]. Energies, 2021, 14(11): 1-15.
[20] BENTO P M R, POMBO J A N, CALADO M R A, et al. Optimization of neural network with wavelet transform and improved data selection using bat algorithm for short-term load forecasting[J]. Neurocomputing, 2019, 358: 53-71.
[21] 梁智, 孙国强, 李虎成, 等. 基于VMD与PSO优化深度信念网络的短期负荷预测[J]. 电网技术, 2018, 42(2): 598-606.
LIANG Zhi, SUN Guoqiang, LI Hucheng, et al. Short-term load forecasting based on VMD and PSO optimized deep belief network[J]. Power System Technology, 2018, 42(2): 598-606.
[22] YU F, XU X. A short-term load forecasting model of natural gas based on optimized genetic algorithm and improved BP neural network[J]. Applied Energy, 2014, 134: 102-113.
[23] 刘建华, 李锦程, 杨龙月, 等. 基于EMD-SLSTM的家庭短期负荷预测[J]. 电力系统保护与控制, 2019, 47(6): 40-47.
LIU Jianhua, LI Jincheng, YANG Longyue, et al. Short-term household load forecasting based on EMD-SLSTM[J]. Power System Protection and Control, 2019, 47(6): 40-47.
[24] 王俊, 李霞, 周昔东, 等. 基于VMD和LSTM的超短期风速预测[J]. 电力系统保护与控制, 2020, 48(11): 45-52.
WANG Jun, LI Xia, ZHOU Xidong, et al. Ultra-short- term wind speed prediction based on VMD-LSTM[J]. Power System Protection and Control, 2020, 48(11): 45-52.
[25] 史加荣, 赵丹梦, 王琳华, 等. 基于RR-VMD-LSTM的短期风电功率预测[J]. 电力系统保护与控制, 2021, 49(21): 63-70.
SHI Jiarong, ZHAO Danmeng, WANG Linhua, et al. Short-term wind power prediction based on RR-VMD- LSTM[J]. Power System Protection and Control, 2021, 49(21): 63-70.
[26] CHEN S, DONG X, PENG Z, et al. Nonlinear chirp mode decomposition: a variational method[J]. IEEE Transactions on Signal Processing, 2017, 65(22): 6024-6037.
[27] CHEN B, WANG Y. Short-term electric load forecasting of integrated energy system considering nonlinear synergy between different loads[J]. IEEE Access, 2021, 9: 43562-43573.
[28] XUE J, SHEN B. A novel swarm intelligence optimization approach: sparrow search algorithm[J]. Systems Science & Control Engineering, 2020, 8(1): 22-34.
[29] ZHU Y, YOUSEFI N. Optimal parameter identification of PEMFC stacks using adaptive sparrow search algorithm[J]. International Journal of Hydrogen Energy, 2021, 46(14): 9541-9552.
Short-term load combination forecasting model integrating ACMD and BiLSTM
YAO Haoran, LI Chengxin, ZHENG Xiujuan, YANG Ping
(College of Electrical Engineering, Sichuan University, Chengdu 610065, China)
To improve the accuracy of short-term load forecasting on the user side, a short-term load combination prediction method based on adaptive chirp mode decomposition (ACMD) and sparrow search algorithm (SSA) optimized bi-directional long short-term memory network (BiLSTM) is proposed. Given the problem of strong fluctuation and non-stationarity of short-term power load, ACMD is used to decompose the short-term load time series into several relatively simple sub-components, and BiLSTM is used to predict each sub-component. At the same time, in order to overcome the problem of unstable prediction results caused by different parameter values of BiLSTM, SSA is used to optimize the hyperparameters of the BiLSTM model. The prediction results of each sub-component are superimposed to obtain the final prediction results.Compared with single prediction model and multiple combination prediction models, the experimental results show that this method has higher prediction accuracy.
load forecasting; BiLSTM; ACMD; sparrow search algorithm; temporal decomposition
10.19783/j.cnki.pspc.211719
国家自然科学基金项目资助(52077146)
This work is supported by the National Science Foundation of China (No. 52077146).
2021-12-16;
2022-03-14
姚浩然(1995—),男,硕士研究生,研究方向为负荷预测;E-mail: 1041819162@qq.com
李成鑫(1976—),男,通信作者,博士,副教授,硕士生导师,研究方向为电力系统自动化及电力大数据分析;E-mail: lcx36@126.com
郑秀娟(1982—),女,博士,副教授,博士生导师,研究方向为模式识别与信号处理。E-mail: xiujuanzheng@ scu.edu.cn
(编辑 许 威)

