一种基于数据剔除与局部偏最小二乘的含油钻井液原油体积分数预测方法
王国良, 王 阳, 李存磊
(辽宁石油化工大学 a. 信息与控制工程学院, b. 石油天然气工程学院, 辽宁 抚顺 113001)
在油气勘探中,录井是一种为石油开采提供钻井信息的过程,通过对信号的采集、储存、处理与分析钻井过程中得到的信息,判断是否存在油气。录井技术是石油勘探中最基础的,同时也是发现、评估油气藏最快、最直接的方法[1]。目前,随着大斜井与水平井应用的次数越来越多,随钻测井成为目前油气勘探的重要手段[2]。它不仅可以适应不同的地下环境,还具有较高的解释精度,在开采过程中减少了资金的消耗,大大提高了工作效率。
在含有原油的混合钻井液中,判断是否存在原油主要是判断烃类物质是否存在。而拉曼光谱分析技术不仅包含丰富的样品检测成分信息,还具有检测样本无损坏、检测速度快、精度高、环境适应性强、易标准化等优点。目前,拉曼光谱技术应用于生物、材料、石油化工等多种领域,是现代分析技术不可或缺的重要部分[3-4]。在石油分析的研究中,包丽丽等[5]用拉曼光谱检测汽油、柴油、石脑油等不同油类光谱图的规律与特点,说明拉曼技术在油类检测中的潜力;姚捷等[6]通过分析甲醇汽油中甲醇含量与光谱的线性关系,建立一种基于拉曼特征峰的回归方程对甲醇汽油中的甲醇含量进行定量计算;刘建美等[7]对原油的光谱图进行分析,证明特征峰的不同可以有效区分不同类型的原油。付洪涛等[8]将激光拉曼应用于钻井液中,通过正辛烷与苯的特征峰建立最小二乘法,证明拉曼光谱可以用于检测钻井液中烃类的体积分数。同时他还将拉曼技术应用于海上风化原油鉴定中,根据出峰位置与特征峰强度快速鉴定原油类别[9]。上述算法中大部分的研究都是根据特征峰位置来判断原油的体积分数,只是证明了拉曼光谱可以应用于原油的检测中,并没有根据光谱的数据特点建立体积分数预测模型,也没有给出结果的准确性。
本文将随钻拉曼检测技术首次应用到石油化工领域,对突破随钻油气测井的技术瓶颈,具有一定的实际意义,而拉曼技术在随钻油气录井中的研究较少,并且如何对反馈回来的拉曼光谱进行快速、准确地分析与判定是当前的首要任务。因此,本文对拉曼光谱直接进行数据建模,提出一种基于皮尔逊相关系数的剔除规则,并结合欧氏距离与偏最小二乘法建立体积分数预测模型。最后,对随钻录井进行仿真实验,配置的含有不同体积分数石油的钻井液混合物并进行拉曼激光的照射得到的光谱数据进行验证。通过结果可以看出,本文提出的算法对数据的拟合程度较好、对混合物体积分数实现了快速、准确的进行分析与判定。
1 原理与算法
本文根据对不同体积分数的含油钻井液进行拉曼光谱的检测得到拉曼光谱图,对得到的光谱图进行光谱处理,分别有拉曼光谱预处理,特征提取,最后建立预测模型。在此基础上,加入了剔除数据的方法,并将偏最小二乘模型进行修改,进一步提高模型准确度。
1.1 小波变换
小波变换是一种对信号进行时频分析与处理的手段[10],输入信号通过小波变换分解出高频部分与低频部分[11],其中,高频部分主要包含了信号中的噪声信息,而低频部分包含了信号用来表达小波数据与原始数据的相近程度的主要信息。通过不断地对低频部分进行分解,最终,选取n+1次分解后低频部分作为信号的特征。离散小波的公式为[12]

(1)
式中:a0、b0表示变换因子;t为时间;k为常量,k∈;ψ为小波母函数。
在光谱分析中数据维数较大,模型容易产生过拟合现象,因此,需要对光谱数据进行特征提取。本文的光谱数据有1 961维,为了缩短程序的运行时间与困难,实现对光谱的快速分析与预测,采用小波变换对数据提取特征,将维数缩短,去除冗余信息,并用于完成后续的分析与建模。
1.2 欧氏距离
欧氏距离是计算高维空间中2点的真实距离的方法,可以简单、直观地判断2组数据距离的远近,欧氏距离的公式如下:
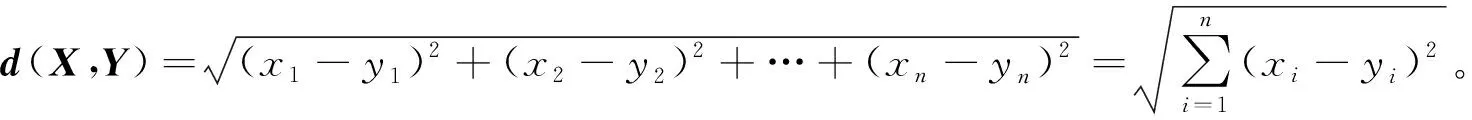
(2)
式中,X,Y表示高维空间中的2组变量。
本文所用的样本体积分数从0~15%,全部参与建模时体积分数跨度较大。因此,通过欧氏距离寻找与待预测数据距离较近的数据作为邻近集,然后将邻近集作为用来建立模型的数据。寻找邻近集的步骤如下:
Step 1 根据式(2)计算待预测数据与已知样本间的欧氏距离;
Step 2 设置欧氏距离的最大值τ,比较欧氏距离的大小,当欧氏距离小于最大值τ时,则属于邻近集,进行建模,反之,则不参与建模。
1.3 皮尔逊相关系数
皮尔逊相关是由Pearson提出,用于判断数据之间相关程度的方法[13-15]。它的绝对值取值范围为0~1。当绝对值等于1时,2组数据完全相关,当等于0时,则2组数据完全不相关,越接近1,表示数据之间的相关性越大[16-17]。计算公式如下所示[18]:
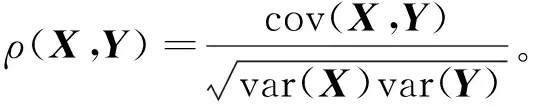
(3)
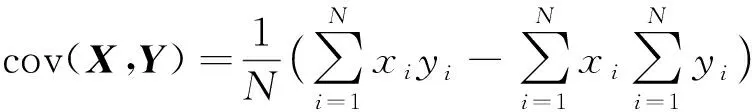
在建模时,模型会受到异常数据或“不合群”数据的影响,造成模型精度较差。针对此问题,选取皮尔逊相关系数建立剔除规则。通过判断数据间的相关程度,对数据进行剔除。现给出剔除规则如下:
Step 1 根据式(3)计算拉曼光谱间的相关系数;
Step 2 设置相关系数的最小值ρmin,比较相关系数的大小,当相关系数小于该最小值ρmin时,即认为2变量间的相关程度低,记为0;
Step 3 设置比例值δ,判断该数据中0的个数占该体积分数下样本个数的比例值,当该比例值大于δ时,则认为该数据应该被剔除,反之,则保留该数据。
1.4 偏最小二乘法(PLS)
偏最小二乘法被称为第2代回归方法,常用于解决变量较多但样本较少或变量之间存在多重相关性的情况[19-20]。在自变量中提取出解释能力强的新变量[21],用于建立偏最小二乘模型。
首先对自变量X=[x1,x2,…,xn]与因变量Y进行标准化得到E0,F0,再提取成分p1,q1,其中,p1=E0w1,q1=F0v1,并且|w1|=1,|v1|=1。成分需要最大程度上表述变量的主要信息,并且相关程度较高[22]。对成分p1建立回归方程,如式(4)、式(5)所示,计算残差E1,F1,最后判断残差是否满足精度要求,不满足则对残差信息E1,F1继续提取成分p2,q2,建立方程,计算残差与判断是否满足精度要求,如此循环,直到精度满足条件,算法停止。最后,对提取出来的成分p1,p2,…,pm建立关于F0的回归模型,得到式(6)、式(7)的方程。由于P=E0W,得到式(8)[23]。最后进行逆标准化并整理得到式(9)。
采用PLS建立模型对混合物的体积分数进行预测,将经过预处理与小波变换后的数据直接建立预测模型时,结果并不理想。因此,本文提出2种算法,证明剔除数据的有效性并进行分析与比较。
1.5 算法流程
在实际操作中, 拉曼光谱在检测时波形很容易被外界因素干扰, 例如: 发射噪声, 仪器噪声及读出噪声等噪声的影响; 样品、容器等荧光背景的影响; 激光强弱与激光散射带来量纲与量级的影响[24]。 因此, 在建立预测模型前需要对光谱进行预处理。 针对上述3种影响, 本文分别采用多项式移动平均值滤波法(Savitzky-Golay)、多项式拟合法、z-score对光谱进行预处理, 去除检测时光谱受到的各种影响。
通过结合光谱预处理、小波变换、欧氏距离、皮尔逊相关系数与偏最小二乘等方法,提出2种算法。
1.5.1 算法1流程
Step 1 读取建模数据;
Step 2 光谱预处理,包括平滑去噪,基线校正,标准化;
Step 3 用式(1)提取特征向量;
Step 4 计算建模数据间的相关系数;
Step 5 判断数据是否满足剔除规则,若满足,则剔除该数据,若不满足,则保存;
Step 6 根据Step 5保存的数据建立PLS预测模型并输出;
Step 7 读取验证数据,并执行Step 2、Step 3;
Step 8 计算验证数据与Step 5中保存的建模数据的相关系数;
Step 9 判断数据是否满足剔除规则,若满足,则剔除该数据,并重新执行Step 7,若不满足,则执行Step 10;
Step 10 将数据输入到Step 6输出的预测模型,预测体积分数并输出。
1.5.2 算法2流程
Step 1 读取建模数据与验证数据;
Step 2 光谱预处理,包括平滑去噪,基线校正,标准化;
Step 3 用式(1)提取数据的特征变量;
Step 4 计算验证数据与建模数据之间的距离;
Step 5 判断建模数据中是否存在距离小于最大值的数据,若存在,则进行Step 6;若不存在,则删除该验证数据,并重新读取验证数据;
Step 6 保存符合条件的建模数据并计算建模数据间的皮尔逊相关系数;
Step 7 比较相关系数的大小,并判断建模数据是否满足剔除规则,若满足,则剔除该建模数据,若不满足,则保存;
Step 8 根据Step 7中保存的建模数据建立PLS预测模型;
Step 9 计算验证数据与Step 7保存的建模数据的皮尔逊相关系数;
Step 10 判断数据是否满足剔除规则,若满足,则剔除该验证数据,并重新读取验证数据,若不满足,则执行Step 11;
Step 11 将满足条件的验证数据输入到Step 8中输出的预测模型中,预测该验证数据的体积分数并输出。
2 仿真实验与结果分析
2.1 数据来源
本文数据来源于实验室配置的含有原油的钻井液混合物。通过配置不同体积分数的原油钻井液混合物,再经过激光拉曼仪的照射得到拉曼光谱图。
1) 实验器材。实验需要的器材有:原油,饱和盐水钻井液,容积为12 mL的透明玻璃瓶若干,水浴锅,规格为10 mL、精度为0.1 mL的量筒2支,比色皿若干,规格为10 mL、精度为0.1 mL的移液器2支,移液器配套的一次性塑料嘴若干,SSR-200拉曼仪。
2) 实验步骤。以含体积分数为10%原油的饱和盐水含油钻井液为例,为方便计算溶质溶剂含量,溶液体积确定为10 mL。
步骤如下:
Step 1 计算饱和盐水钻井液中原油和饱和盐水钻井液的含量,以原油体积分数为10%为例,溶液体积10 mL,所以得到原油1 mL,饱和盐水钻井液9 mL。
Step 2 选取规格为10 mL的量筒,量取9.0 mL饱和盐水钻井液,由于液面凹陷,液面边缘需略高于9.0 mL的刻度(液面边缘到达9.1 mL左右即可),测量准确后转移至玻璃瓶中,再用移液器抽取原油1.0 mL,转移至装饱和盐水的玻璃瓶内,封盖摇匀。
Step 3 将配好并封闭的含油钻井液放至水浴锅加热30 min,水浴锅温度设置为80 ℃,每隔10 min将玻璃瓶取出,摇匀后继续加热。
Step 4 将加热完毕的钻井液倒至比色皿中(溶液体积占比色皿的80%即可),将比色皿置于拉曼仪配套的卡槽中(营造密闭黑暗的环境,防止光线及噪声干扰)。
Step 5 准备完毕后打开拉曼仪,电脑选择连接拉曼仪的WIFI频道,在拉曼仪发出嘀声之后,点击开始即可测量拉曼曲线。
现有4组体积分数,分别是0,5%,10%,15%,每个体积分数下有40组拉曼光谱数据,总共160组数据,并且每组数据的长度为1 961维。
图1是分别从4个体积分数中选取部分数据,从图中可以看出,不同体积分数的波形是不同的,并且特征峰的位移也不一样。
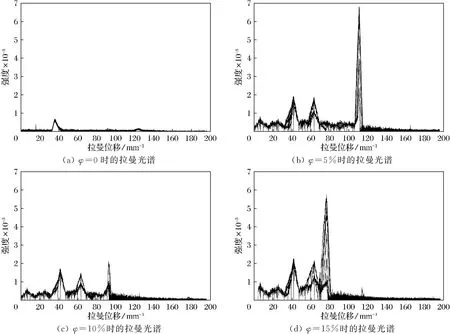
(a) φ=0时的拉曼光谱(b) φ=5%时的拉曼光谱(c) φ=10%时的拉曼光谱(d) φ=15%时的拉曼光谱
为了进行建模与验证,将现有的光谱数据分为2部分,一部分(30组)用来建立PLS体积分数预测模型,即建模数据,另一部分(10组)用来对预测模型进行验证,即验证数据,二者共同记为数据1。为了验证模型的有效性,再次将数据打乱,重新分出建模数据与验证数据,记为数据2,同理得到数据3。
2.2 模型评价指标
为了评价预测模型的精准度,选择平均绝对误差(EMAE)、均方误差(ERMSE)和可决系数(R2)这3个性能指标对模型结果进行比较与评价。公式如下:
式中:fi表示模型的预测结果;yi表示真实值;Myi表示真实值的平均值。
2.3 PLS直接建模的结果
为了对比全面,本文将从图像与性能指标上分别对3组数据进行对比。图2为直接建模的结果。

(a) PLS建模结果(b)PLS验证结果
从图2中可以看出,建模结果与验证结果的拟合程度非常差,存在很多误差较大的点。根据程序仿真中的时间为49.5 s。在实际应用中,从检测数据到提取数据最后模型预测,这些时间的消耗是非常大的,不能达到快速地要求,因此需要对模型进一步修改。
2.4 算法1的实验对比结果
图2表明,直接进行PLS建模的结果并不理想。为了提高模型精度,本文提出一种基于皮尔逊相关系数的剔除规则,对数据进行一定的删减,结果如图3~图5及表1所示。

(a) 不含剔除数据建模结果(b) 不含剔除数据验证结果(c) 含有剔除数据验证结果
从图3~图5中可以看出,剔除规则可以删掉误差较大的点,并且剔除后再建模的预测结果与真实值较为接近。为了进一步说明剔除数据的有效性,表1给出了剔除数据前后的性能指标。

(a) 不含剔除数据建模结果(b) 不含剔除数据验证结果(c) 含有剔除数据验证结果
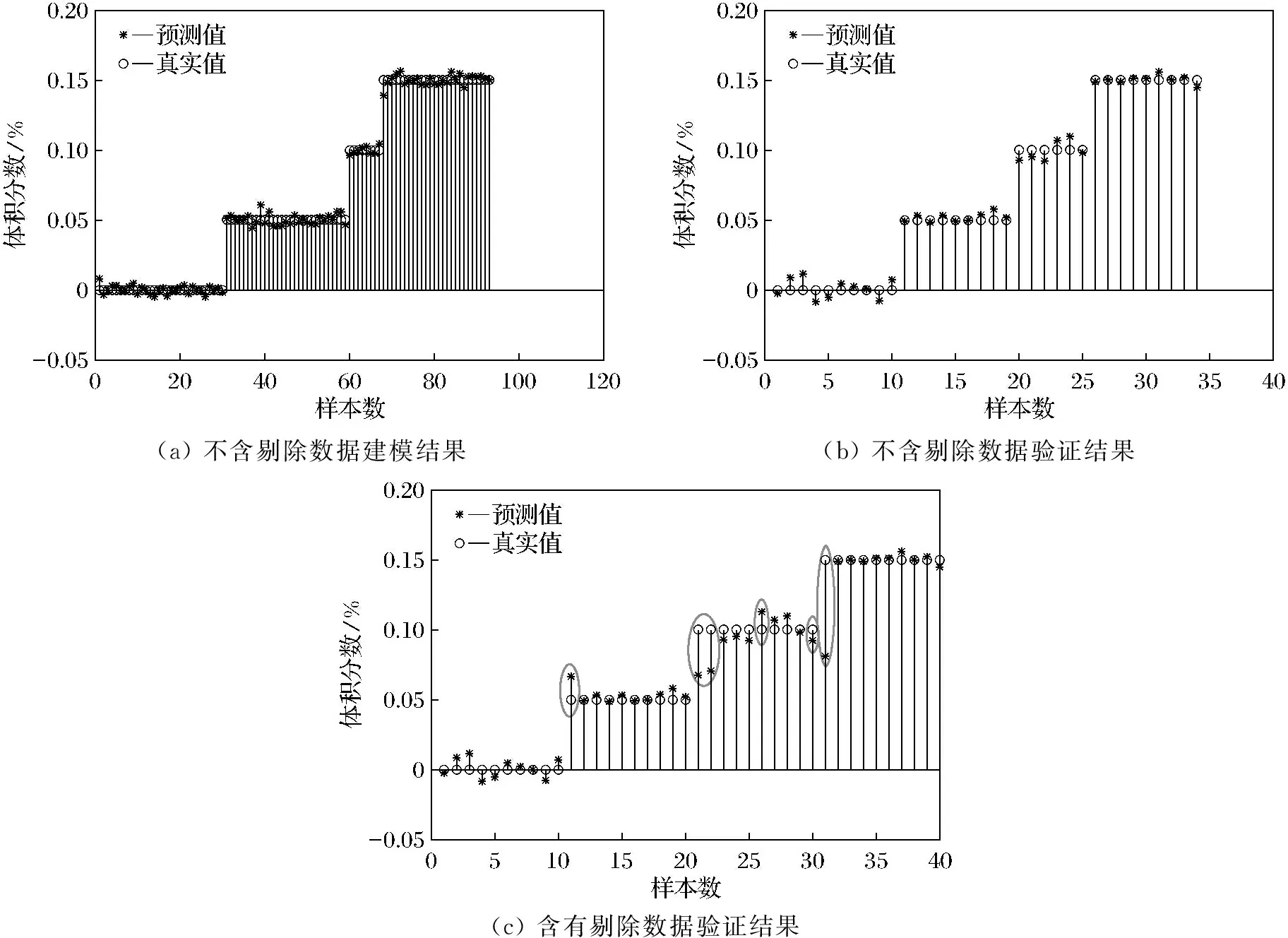
(a) 不含剔除数据建模结果(b) 不含剔除数据验证结果(c) 含有剔除数据验证结果
从表1中可以看出,3组数据进行剔除后模型的精度有了明显的提高。其中,提升最明显的是数据2,R2提高了0.052 7,ERMSE、EMAE分别减少了0.009 2与0.005 6。并且程序的运行时间缩短为不足3 s,说明剔除数据后模型对数据的拟合程度更好,精确度更高,并且程序的运行速度非常快,再一次说明证了明剔除数据的有效性。
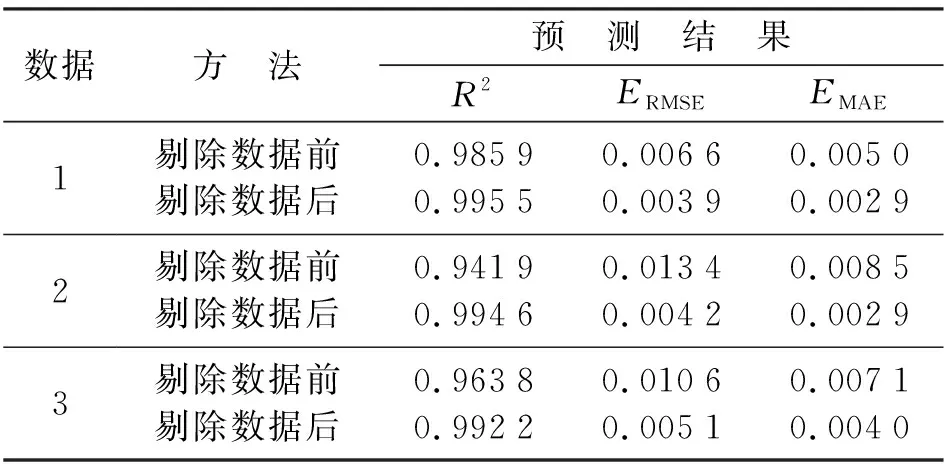
表1 3组数据剔除数据前后性能指标的对比
2.5 算法1与算法2的对比结果
引入剔除规则后,模型的精度有了明显的提高,但从图3~图5中可以看出,模型对部分体积分数数据的拟合效果很好,但有一部分的拟合效果却不理想。我们认为可能因为体积分数的跨度较大,模型对数据的包容性较大,从而精度不够。因此,为了使模型更具针对性,根据与待预测数据距离的大小找到邻近集,建立预测模型。同样对3组数据进行验证,并与算法1的结果进行对比。如图6~图8所示。

(a) 算法1的结果(b) 算法2的结果

(a) 算法1的结果(b) 算法2的结果

(a) 算法1的结果(b) 算法2的结果
从图6~图8中可以直观地看出,3组数据验证的结果中体积分数为0与5%的验证结果非常好,几乎与真实体积分数重合。与算法1相比,说明这2个体积分数选择用于建模的数据与待预测数据很接近,模型更具有针对性。表2可以从数值上对比性能指标的好坏。
从表2中的数据对比结果可知,算法2的性能指标都有提高。数据3提升得最为明显,其中R2提高了0.006 2。而ERMSE与EMAE分别减少了0.002 8和0.001 8。说明采用邻近集数据进行建模时,模型精度会进一步提高,并且更加可靠。进一步证明对数据进行剔除与选择部分数据建立预测模型的必要性。
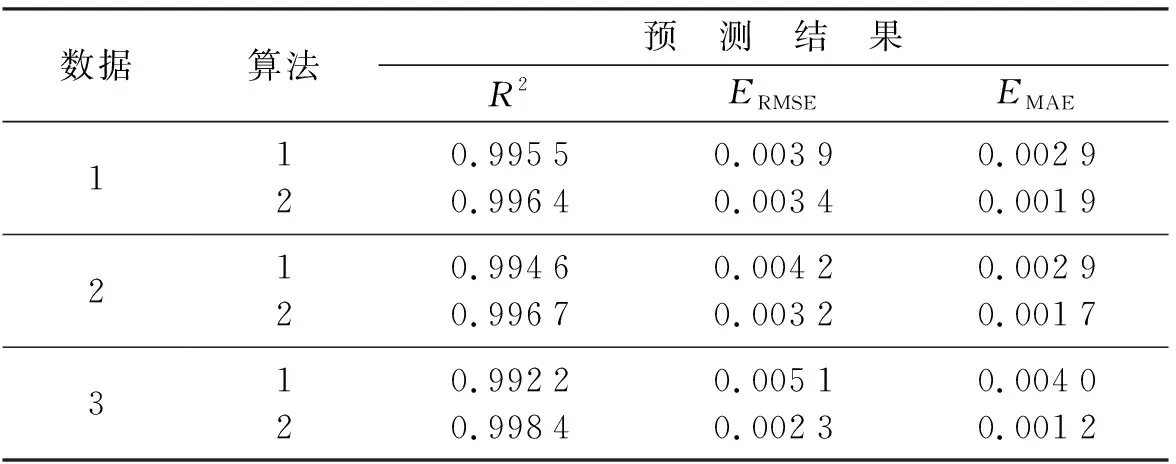
表2 3组数据中2种算法的对比
3 结 论
本文首次将拉曼光谱与随钻油气检测相结合,实现油气快速检测,针对含油钻井液原油的体积分数预测问题,提出了一种基于皮尔逊相关系数剔除规则的方法,并与欧氏距离、PLS相结合,用于对混合物进行体积分数预测。通过2种算法的对比结果,根据算法2建立的预测模型具有更高的精度。当数据经过光谱预处理后,进行小波变换提取特征,再通过欧式距离与皮尔逊相关系数,建立一种基于数据剔除的局部偏最小二乘预测模型,完成对含油钻井液原油体积分数的定性分析与定量计算。预测结果的误差平均在0.2%的范围内,时间缩短至3 s之内,在一定程度上实现了对混合物体积分数快速、准确的判断与分析。

