碳税政策下基于BFA-ACO的冷链物流路径优化

张天瑞, 刘海波

(沈阳大学 机械工程学院, 辽宁 沈阳 110044)

国内的冷链物流起步比较晚,但是由于市场的庞大,近年来,冷链物流飞速发展。然而目前国内的许多冷链物流企业对国家的标准落实不到位,设备相对落后、技术水平较低[1]。由于冷冻产品容易腐坏,这就需要冷链物流在一定时间内完成配送,保证客户的满意度[2]。基于此,施文嘉等[3]采用免疫优化算法确定最优路径方案,对车辆行驶路线进行优化,进而更好地满足客户的需求,但是在规划过程中需要考虑的因素比较多,任务量较大。吕成瑶等[4]以客户满意度为约束条件,使用模拟退火算法,对接受概率调整进行仿真实验,提高了算法的局部精度和收敛速度,该算法求解速度快,简单直观,但是不稳定,效果往往取决于具体问题和设计者经验。

康凯等[5]认为可以使用将碳成本化或者将碳排放作为目标函数进行建模来解决路径优化问题。Rahim等[6]提出了一个同时考虑利润、服务水平和环境的多目标库存路径模型,以运输、装卸过程中的温室气体排放量衡量环境目标。Raua等[7]通过与车辆负载相关的燃油消耗量来计算碳排放,设计了最小化成本和最小化碳排放的双目标模型。以上方法都取得了很好的效果,但往往忽略了碳排放量不仅由燃油产生,还要充分考虑制冷设备所产生的碳排放量。

在算法应用上,曹阳等[8]对人工蜂群算法加以改进,改进后的算法相较于传统算法简单易实现,提高了算法的全局优化能力。另外遗传算法也被广泛应用于路径优化问题当中,范立南等[9]针对农产品配送的特性,采用改进的遗传算法求解冷链物流配送模型,但这容易出现过早收敛的问题。

针对以上问题以及2020年新冠肺炎疫情期间冷链物流的特点,本文在构建冷链物流路径优化模型时,将制冷机器以及行驶过程中所产生的碳排放量考虑到碳税成本当中,综合考虑车辆固定成本、运输成本、制冷成本、碳税成本、消毒成本、货损成本以及时间惩罚成本,同时考虑由于消毒造成的货损成本以及时间惩罚成本所带来的影响,建立一个综合成本最低的冷链物流路径优化模型。另外将细菌觅食算法和蚁群算法结合对路径优化模型进行优化求解,并将所得结果与蚁群算法、遗传算法以及人工蜂群算法所求得的结果进行比较,分析它们的寻优能力、搜索速度以及稳定性。

1 考虑碳税的冷链物流路径优化模型

1.1 问题描述

在低碳环保的前提下,需要充分考虑碳排放所带来的成本。另外,在2020年新冠肺炎疫情期间,多地新冠疫情的出现与冷链物流相关,因此必须增加额外的消毒成本遏制病毒传播。然后充分考虑其他成本,以综合成本最低为目标,构建冷链物流路径优化模型。

1.2 模型假设和约束条件

为将问题抽象为模型,需要做一些假设和约束:

1) 由一个配送中心向多个客户配送;

2) 配送中心能够满足所有客户的需求量;

3) 文中配送运输的货物仅为冷冻海产品;

4) 假设冷藏车辆都匀速行驶,配有冷藏设备且温度不变;

5) 每辆车所载海产品重量不能超过车辆的最大负荷;

6) 运输车辆每次只完成一次配送任务;

7) 已知每个客户的位置和配送量;

8) 每辆车均使用相同型号的消毒设施与消毒液。

1.3 模型构建

本文的综合成本由7个部分组成。

1) 车辆固定成本。固定成本包括车辆的折损成本。设定共有n辆车,第m辆车的固定成本用fm表示。用C1表示运输成本,

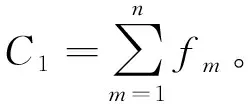
(1)

2) 运输成本。运输成本包括车辆的保养维修成本以及运输过程中的燃油成本。第m辆车每千米的费用为cm,配送中心和客户点的距离为dij,则冷藏车的运输成本C2表示为

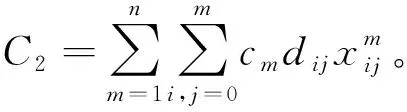
(2)

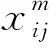
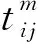
(3)

装卸中的制冷成本C32为

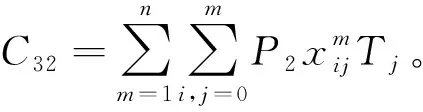
(4)

式中,Tj为装卸时间。则总制冷成本C3为

C3=C31+C32。

(5)

4) 碳税成本。碳税成本是指运输车辆和制冷设备所产生的碳排放成本。冷藏车辆空车时油耗为ε0,满载时单位距离的油耗为ε1,载货量为qij,二氧化碳的排放系数为e,单位碳税价格为Pc,制冷器单位时间内的能耗为E2,最大荷载量为qM。冷藏车单位距离油耗E1为

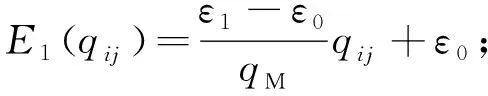
(6)

运输车辆所产生的碳税成本C41为

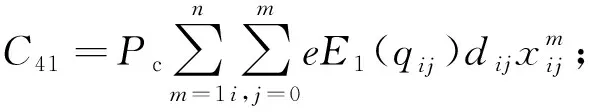
(7)

制冷设备所产生的碳税成本C42为

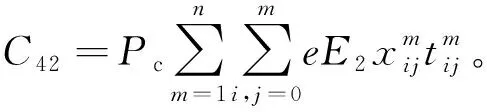
(8)

则总的碳税成本C4为

C4=C41+C42。

(9)

5) 消毒成本。消毒成本指的是在2020年新冠肺炎疫情期间对冷藏车辆以及冷冻产品进行消毒以及检验所产生的费用。消毒费用与货物面积呈正相关。设定冷藏车辆及人员的消毒成本为C51,货物的检验成本为py,冷藏车辆的表面积为Sm,单位面积内消毒液的价格为px,则消毒成本为

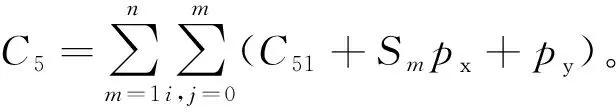
(10)

6) 货损成本。货损成本指产品质量发生变化产生的成本。然而在2020年新冠肺炎疫情期间,还需额外考虑在消毒过程中产生的货损成本以及新冠病毒引起货物损坏的成本。设单位产品的价格为p1,载货量为Qj,运输过程中货物的损坏率为a1,卸货过程中货物的损坏率为a2,卸货时间为Tj,消毒过程中货物的损坏率为b6。则运输之前消毒过程中产生的货损成本为

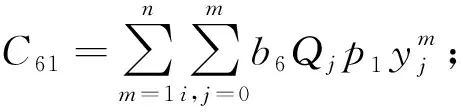
(11)

运输过程中的货损成本为

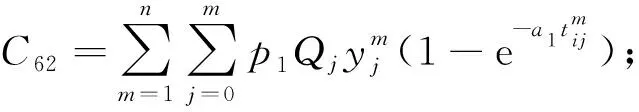
(12)

卸货过程中的货损成本为

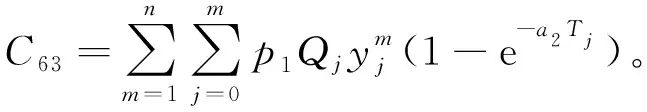
(13)

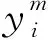
C6=C61+C62+C63。

(14)

7) 时间惩罚成本。时间惩罚成本指的是运输车辆因未在合理的时间内将货物送达地点所产生的成本。在2020年新冠肺炎疫情期间,需要对车辆以及对产品进行额外的消毒检查,这在一定程度上会影响时间惩罚成本。设定消毒以及检查时间为tα,冷藏车辆过早到达客户点所产生的单位时间内等待成本为pw,过晚到达客户点所产生的单位时间内的迟到成本为pc。设可以接受的时间为[T接,T′接],期望时间为[T期,T′期]。

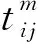
综上所述,综合成本为

C=C1+C2+C3+C4+C5+C6+C7。

(15)

因此,本文所构建的碳税政策下冷链物流路径优化模型为

约束条件如下所示:

2 算法流程设计

2.1 遗传算法(GA)

遗传算法是利用染色体交叉变异的过程来模拟运算的。这一过程主要包括选择、交叉和变异3个过程,通过编码的方式将数据转化为基因结构。这一算法在路径优化问题中得到了广泛的应用。

2.2 人工蜂群算法(ABC)

人工蜂群算法是一种通过研究蜜蜂觅食的行为所提出的一种优化算法。人工蜂群算法的特点是不必掌握相关问题的特殊信息,只需要比较问题的优劣,然后通过各个个体人工蜂进行寻优,从而在蜜蜂种群中得到最优值。

2.3 蚁群算法(ACO)

蚁群算法具有正反馈机制、收敛速度快的优点,但是容易搜索范围较小。而细菌觅食算法的全局搜索能力强,因此可以通过比较2种算法的优点,将它们相结合。

2.4 细菌觅食蚁群算法(BFA-ACO)

当蚁群访问所有节点时,它将形成一条对应的路径,然后根据每个路径中细菌的位置来计算蚂蚁所走的总路径。长度就是细菌的健康状况。 然后,根据细菌的健康程度对细菌进行排名,而健康状况最好的细菌是这种迭代的最佳解决方案。 通过繁殖种群中最健康的细菌,同时消除最不健康的细菌,从而增强收敛速度和全局收敛性。

2.5 算法流程优化设计

在本文中,细菌觅食-蚁群算法在优化求解的时候需要以下7个步骤:

1) 初始化每个参数,将蚂蚁一个一个映射到细菌上,然后计算节点之间的距离矩阵;

2) 将n只蚂蚁随机放置在m个节点上,在满足时间窗、载货量、客户需求和产品安全的约束下,然后计算出蚂蚁从i到j的可能性,然后将访问节点加入到记录表中,反复此过程,直至所有蚂蚁重新回到原点;

3) 计算每只蚂蚁经过路径的长度Lk和总成本C;

4) 加入复制过程。按路径长度Lk的降序对细菌进行排序,消除路径长度较短的部分细菌,然后将剩余的细菌中较小的Lk复制成2个相同的细菌;

5) 引入趋化操作,然后翻转细菌,路径长度发生变化时记录当前的最佳路径长度;

6) 根据式(23)对路径上的信息素进行更新,重新录入路径记录表,并回到步骤2)中继续迭代;

7) 当迭代次数达到指定的最大值时,停止迭代并记录最终总成本和路径。

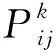
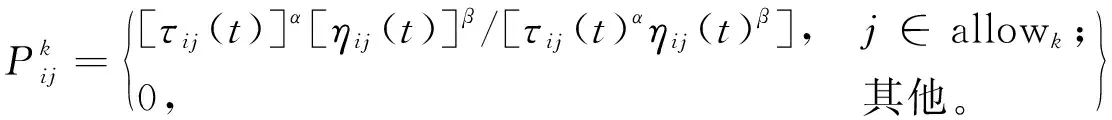
(22)

信息素浓度的更新机制为

(23)

式中,ρ表示信息素挥发程度,信息素总量为Q。

细菌i的每一步趋向操作为

(24)

设定进行NC次趋化操作,细菌的健康度函数为Hi。则健康函数为

(25)

在遗传算法优化求解过程中,需要以下步骤。

1) 对相应的配送中心和客户点进行编码。遗传算法在将解空间的数据转化为基因结构时,需要通过编码的方式来完成,即通过编码的方式表示染色体。不同基因可以组成不同的染色体,通过找到最优的染色体来找到最优解。在遗传算法中,有多个可以进行编码的方式,本文选择自然数编码的方式来优化次序。自然数编码即表示通过对客户进行自然数的排序进行编码,此方法反映问题结构比较直观,操作简单。

设定运送中心有n辆冷藏车辆,为m个顾客进行配送,则可以形成一个长度为n+m+1的染色体,

{0,i11,i12,…,i1a,0,i21,i22,…,i2b,…,0,im-1,1,im-1,2,…,im-1,n-1,0,im1,im2,…,imn,0}。

(26)

式中,0表示配送中心,该条染色体表示在配送中心处有n辆冷藏车辆准备配送,两个0中间的客户点形成一条配送路径,尾部的配送中心将所产生的路径与下一条路径分隔开。以一个配送中心对9个客户点进行配送为例,随机进行编码,形成一条染色体:0547012930680,第一条路径表示车辆从配送站出发,进行配送的客户依次为5、4、7;第二条路径表示车辆从配送站出发,进行配送的客户依次为1、2、9、3;第三条路径表示车辆从配送站出发,进行配送的客户依次为6、8。

2) 将种群初始化。

3) 选择合适的适应度函数,文章采用成本倒数的10 000倍作为适应度函数值。

4) 将适应度值大的染色体进行复制。

5) 采用循环点交叉。

6) 进行变异操作。

7) 达到规定最大迭代次数值,输出结果。

人工蜂群算法运行过程包括以下步骤。

1) 算法在开始时,设置一定数量的食物源,即客户点。确定引领蜂(运输车辆)的数量,食物源为xi。

2) 计算每个食物源的适应度的值。

3) 让引领蜂在邻域进行搜索,搜索公式为

vij=xij+rij(xij-kij)。

(27)

式中,vij为候选的食物源,v0表示起点的位置,每一个vi都对应一个客户点。rij是在[-1,1]上随机产生的。另外,k和j也都是随机产生的,且两者互不相等。然后评估适应度值。

4) 计算出引领蜂的选择概率。每个蜜源被选择的概率为

(28)

5) 如果一个食物源循环的次数超过了上限且依旧保持不变,这个食物源就没了价值,需要被放弃选择新的食物源。在此同时,引领蜂就要完成侦查蜂的任务,这个更新过程为

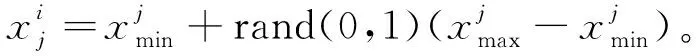
(29)

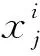
li+1=li+1。

(30)

6) 当存在li=limit时,则舍弃这个解,然后由侦查蜂搜索新的可行解。设定迭代次数的最大值,当达到这一规定值时输出解;否则,回到第3)步继续运行。

3 算法测试与仿真

3.1 算法测试与分析

1) 寻优能力分析。本文使用MATLAB 2016b对TSPLIB标准库中的5个经典数据集[10]进行仿真测试,并与蚁群算法与遗传算法的优化结果进行对比,从而测试出细菌觅食-蚁群算法求解路径优化问题的性能。

设置本次测试的最大迭代次数Nmax为100,根据最经典的商旅问题进行测试。设定已知m个不同地点,每个地点之间距离为dij,每个地点只被访问一次,完成所有地点的访问时记录最短路径。设定蚁群的规模为m=2n,然后通过正交试验[11]选取算法参数,设定α=1,β=5,ρ=5,Q=100。定交叉概率Pc=0.4,变异概率Pm=0.06。

通过使用GA、ABC、AOC及BFA-ACO对以上数据集求解10次,所得结果如表1和表2所示。

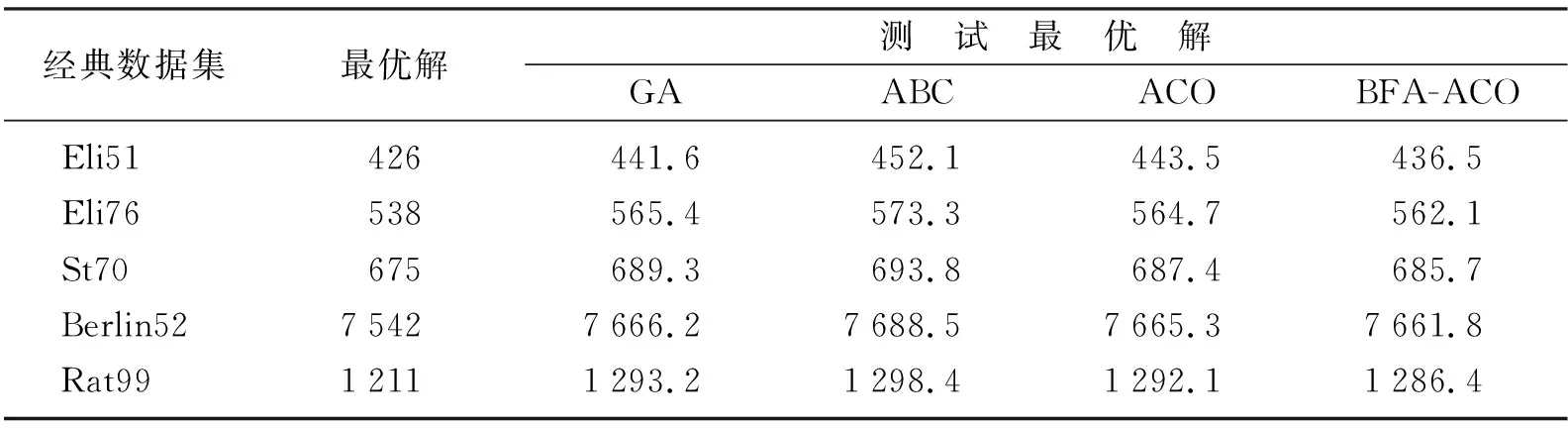
表1 测试最优解Table 1 Test optimal solution

从表1和表2中可以看出,BFA-ACO所求得的测试最优解和平均值最小。寻优能力更好。

2) 收敛速度和可靠性。一般情况下,通过使用平均收敛代数和成功率来表示算法的收敛速度和可靠性,结果如表3、表4所示。

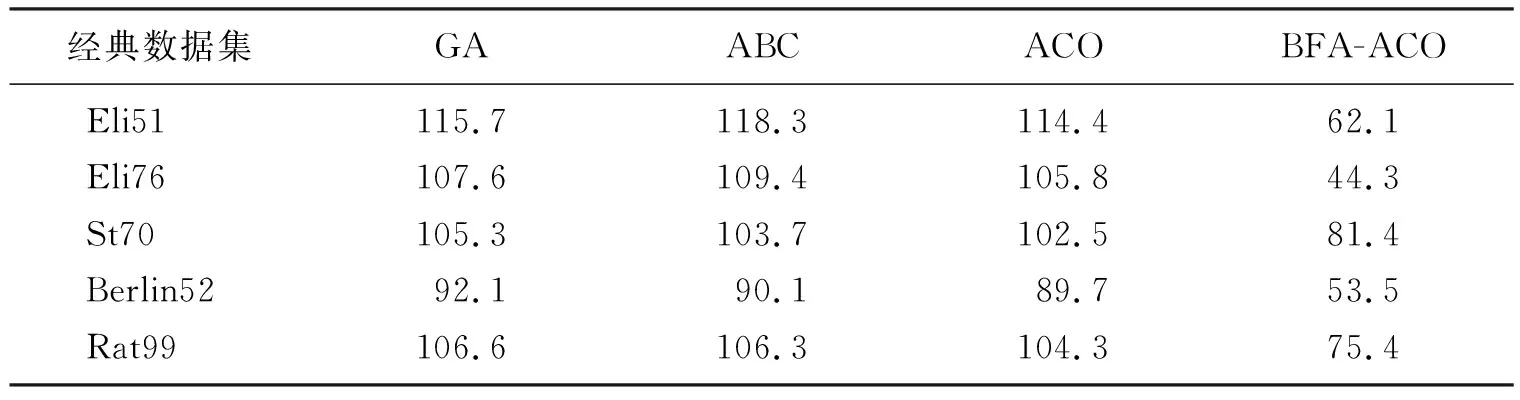
表3 平均收敛代数Table 3 Average convergence algebra

从表3和表4可以看出,通过 BFA-ACO所求得的平均收敛代数均小于使用基本蚁群算法、遗传算法和人工蜂群算法所求得的结果,另外细菌觅食-蚁群算法所求得的5个数据集成功率均为100%,均高于其他算法所求结果,收敛速度和可靠性最优。

3.2 实验仿真

本文以F冷链公司为例,向10个客户配送。每次配送由一个配送中心向10个客户点进行。需求量和时间如表5所示。

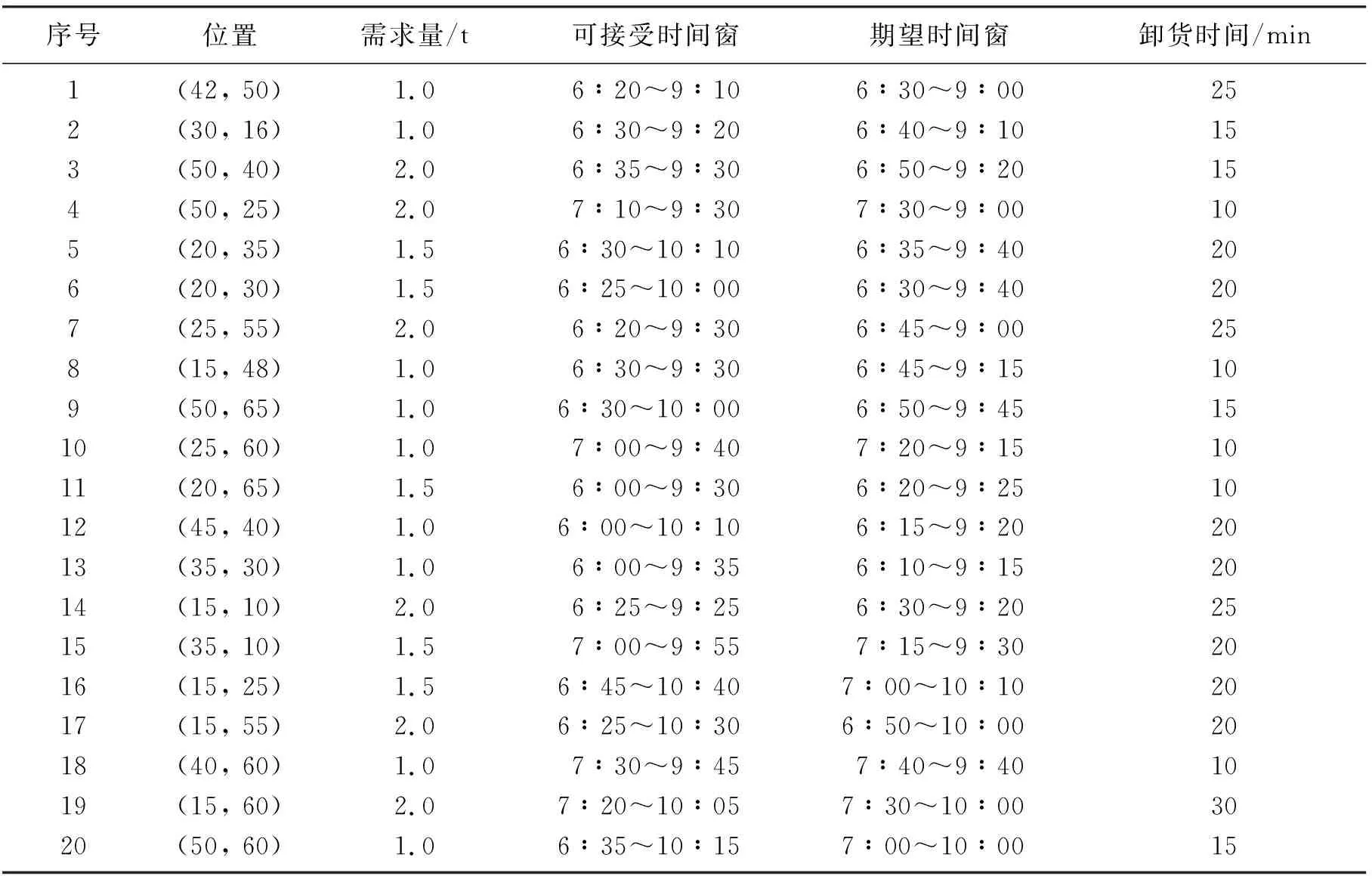
表5 需求量和时间Table 5 Demand and time

在本文的模型中,已知每辆车的最大载荷量为10 t,固定成本C1=500元,运输成本C2=4元·km-1,运输过程中的制冷成本C31=10元·h-1,装卸货过程中的货损成本C32为15元·h-1,平均行驶速度为50 km·h-1。运输的冷冻产品的单位价格为4 000元·吨-1,消毒过程中的货损率b6=0.005,运输过程中冷冻产品的变质率a1=0.01,装卸过程中产品的变质率a2=0.03。单位碳税的价格Pc=15元·kg-1,二氧化碳的排放系数e=2.66 kg·L-1,运输车辆在空车时候的油耗ε0=16 L·km-1,车辆满载时,油耗ε1=20 L·km-1,制冷机器的能耗E2=0.002 5 L·(t·km)-1。单位面积内消毒液价格px=5元·m-2,冷藏车辆的表面积Sm=50 m2,每辆车货物的检查成本py=10元。

根据上述参数,以M公司为例,分别使用GA、ABC、AOC及BFA-ACO对所建立的考虑碳税的冷链物流路径优化模型进行求解20次,综合成本的求解结果如表6所示。

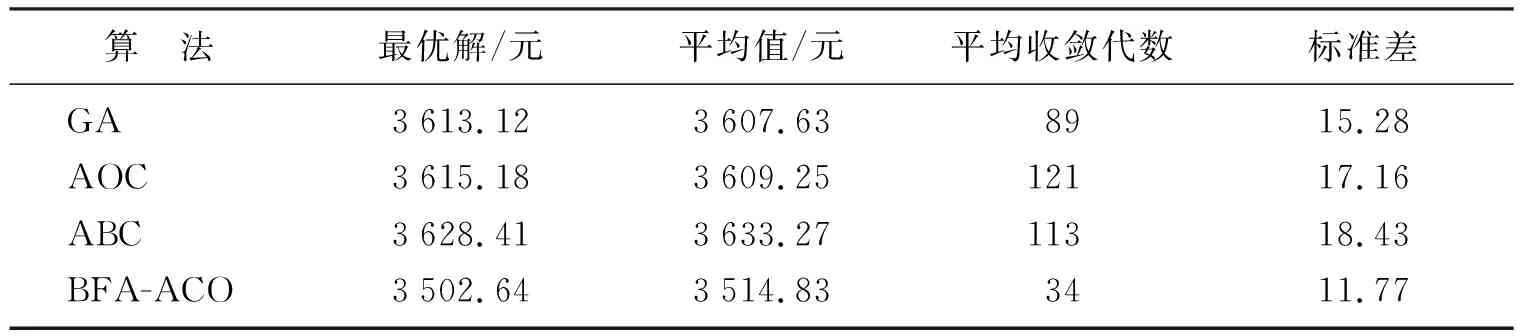
表6 综合成本求解结果Table 6 Solution results of comprehensive cost

从表6可以看出,使用BFA-ACO混合算法的最优解、平均值以及标准差均比GA、ABC、AOC求得的结果小。

由蚁群算法求得的路径如图1所示。

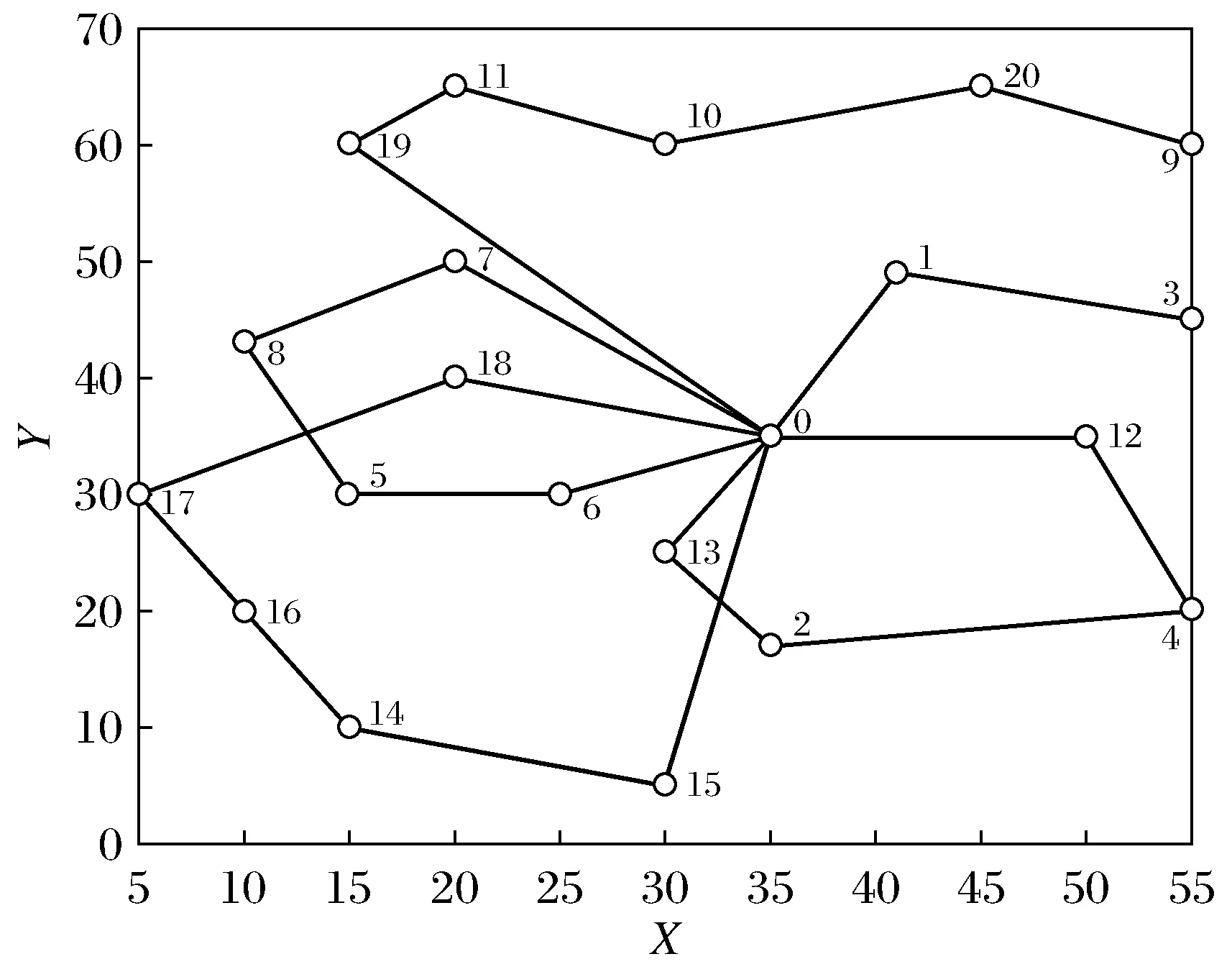
图1 基本蚁群算法求得的路径

由人工蜂群算法所得的路径如图2所示。

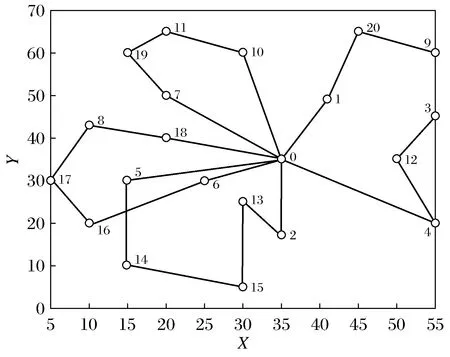
图2 人工蜂群算法求得的路径

由遗传算法所得的路径如图3所示。

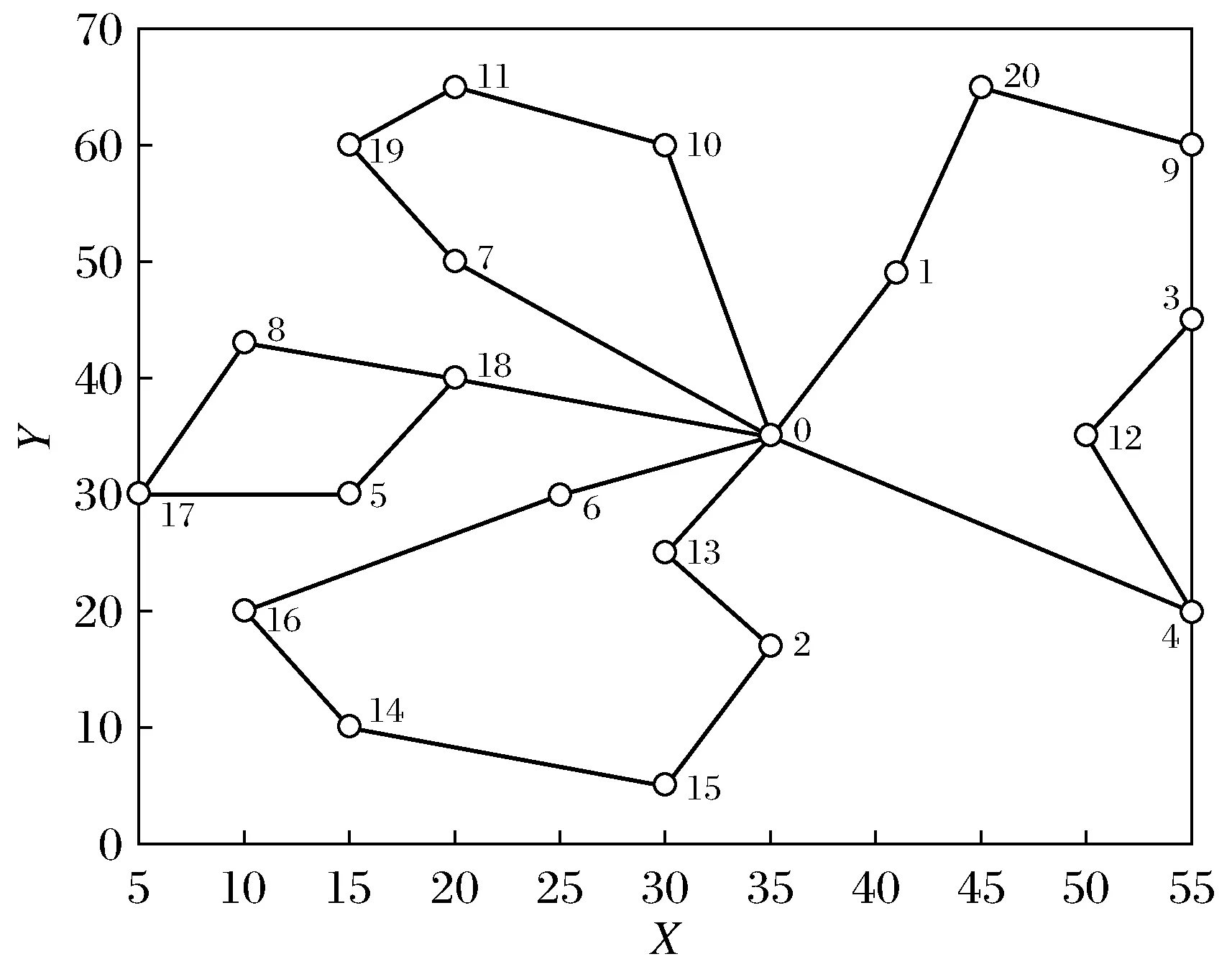
图3 遗传算法求得的路径Fig.3 Path map obtained by genetic algorithm

使用细菌觅食-蚁群算法所得的路径如图4所示。

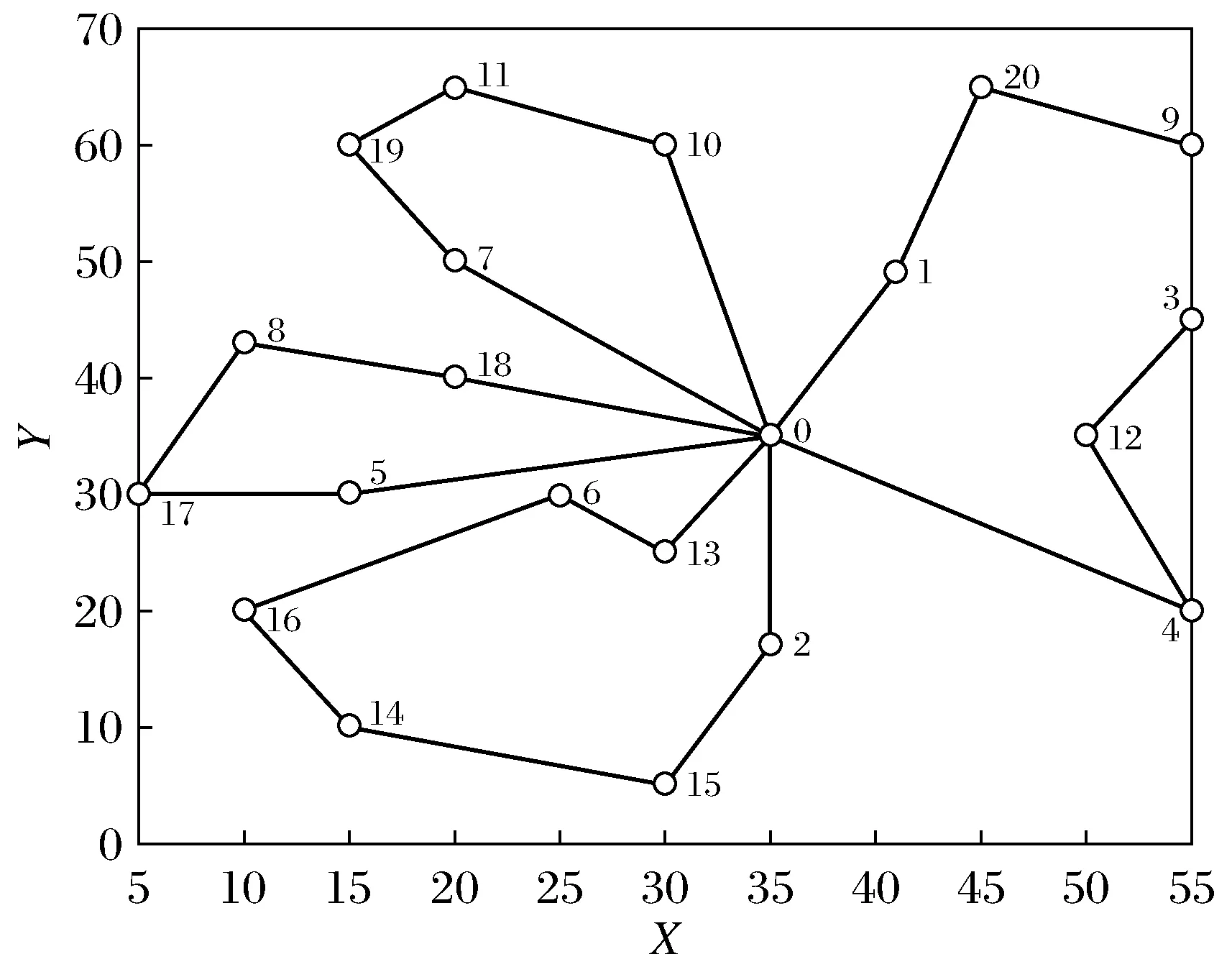
图4 细菌觅食蚁群算法所求得路径Fig.4 Path diagram obtained by BFA-ACO algorithm

其中X、Y轴分别代表配送中心和客户位置的横纵坐标,0代表配送中心,1～20分别代表20个客户点,共需4辆冷藏车辆进行配送。根据图1～图4对比可得,通过细菌觅食-蚁群算法所求得的路径避免了不必要的交叉,使得最短路径对应的总成本最低。

以算例Eli51为例,从收敛过程对比使用4种算法求解路径优化问题的效果如图5所示。

图5 收敛过程对比图Fig.5 Comparison of convergence process

由图5可知,细菌觅食-蚁群算法的收敛速度和精度最优。另外,使用细菌觅食-蚁群算法仿真求解过程的收敛速度、和稳定性最好,所求得的路径最短,避免了不必要的交叉,综合成本也最低。

4 结 论

随着节能减排的进一步推进以及新冠肺炎疫情的持续,在冷链物流配送问题当中充分考虑碳排放成本和消毒成本是十分必要的。本文通过碳税交易制度计算出运输以及装卸过程中所产生的碳排放成本,考虑消毒成本以及消毒对时间惩罚成本和货损成本产生的影响,为冷链物流行业发展提供参考依据,相关结论如下:

1) 建立了综合车辆固定成本、运输成本、制冷成本、碳税成本、消毒成本、货损成本以及时间惩罚成本的冷链物流路径优化模型。

2) 细菌觅食算法与蚁群算法结合,加快了收敛速度;将趋化操作加入到蚁群算法中,避免了出现局部最优的缺陷,并且解决问题的效率更高、综合成本最小,能够为求解冷链物流路径优化模型提供理论参考。

3) 通过MATLAB数据集进行算法测试,测试结果表明通过细菌觅食-蚁群算法的求解优化效果最优。

4) 通过实例进行了实验仿真,仿真结果显示使用混合算法求解的路径更短,综合成本最低。

由于新冠病毒在短时间将继续存在,冷链物流行业应当高度重视消毒检验环节,完善追溯技术,在源头上把控产品的品质。