惠斯通电桥的桥臂电阻在考虑测量精度下的选择

徐佳琪，邵 云

(南京晓庄学院 电子工程学院，江苏 南京 211171)

惠斯通电桥是一种常用的测量普通中值电阻的仪器与方法，其主要思想是补偿的思想，有效地避免了中学物理中伏安法测电阻的安培表内接与外接的引入误差，因此具有较高的精确度。但是惠斯通电桥依然存在结构设计上的系统误差，主要体现在桥臂阻值的选择所导致的灵敏度误差和电阻阻值本身的误差。

尽管此前已有多名学者在研究电桥的精确度时，针对电桥的灵敏度进行了详细的探讨并得出了定性甚至定量的研究结果，但是他们大多没有考虑到电阻箱阻值的准确度对于实验结果的影响[1-4]。本文将同时考虑灵敏度与电阻箱阻值的准确度这两个方面对于惠斯通电桥测量精度的影响，计算出测量最为精确即系统误差最小时桥臂的阻值状况。

1 惠斯通电桥的实验原理及其灵敏度

惠斯通电桥测电阻的原理如图1所示，其中Rx为待测电阻，Rs为比较臂，R1、R2为比例臂，电源(设无内阻)电压设为E，G为检流计。

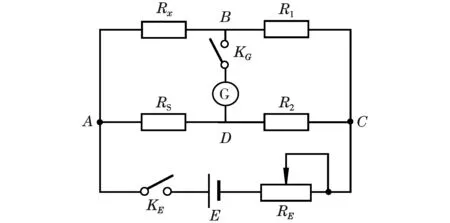
图1 惠斯通电桥的原理示意图

如图1，当电桥平衡(B、D两点等电位，即UBD=0)时，可推导出待测电阻Rx为

(1)

此时电桥的灵敏度必然会影响到测量结果的精确度。根据文献[5,6]，当使用检流计检测电桥平衡时，惠斯通电桥的灵敏度可以表达为

(2)

其中Si为检流计的灵敏度，Rg为其内阻。

(3)

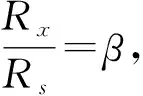
(4)

2 电阻箱带来的误差

实验室常用的直流多值电阻箱误差的主要来源是示值误差ΔR，而ΔR的大小则由电阻箱的准确度f所决定。对于大多数电阻箱来说，由于各档准确度fj的不同，ΔR的大小表示为[7]

(5)

其中Rj为电阻箱各档所显示的电阻值。现以实验室常用的可调范围0～99 999.9 Ω的6档ZX21型电阻箱为例，其各档准确度fj值见表1(注：不同厂家数值略有不同)。100.0 Ω电阻的相对误差显然为0.1%，而99.9 Ω电阻的相对误差

则为

可见电阻箱所示电阻的相对误差并不随阻值连续变化。

表1 ZX21型电阻箱各档阻值的准确度 fj

利用Excel软件，将100～1 000Ω步进5Ω的电阻值及表1中数据代入式(5)，即可计算出其间诸电阻的绝对误差和相对误差，进而作出相对误差随电阻变化的大致曲线如图2所示。鉴于曲线呈不连续的锯齿状，为了简化问题从而获得定性或者半定量的有价值的结果，我们采用了指数函数对该误差曲线进行了拟合，得到如下近似的相对误差函数(同样适用于1 000～10 000Ω)：

(6)

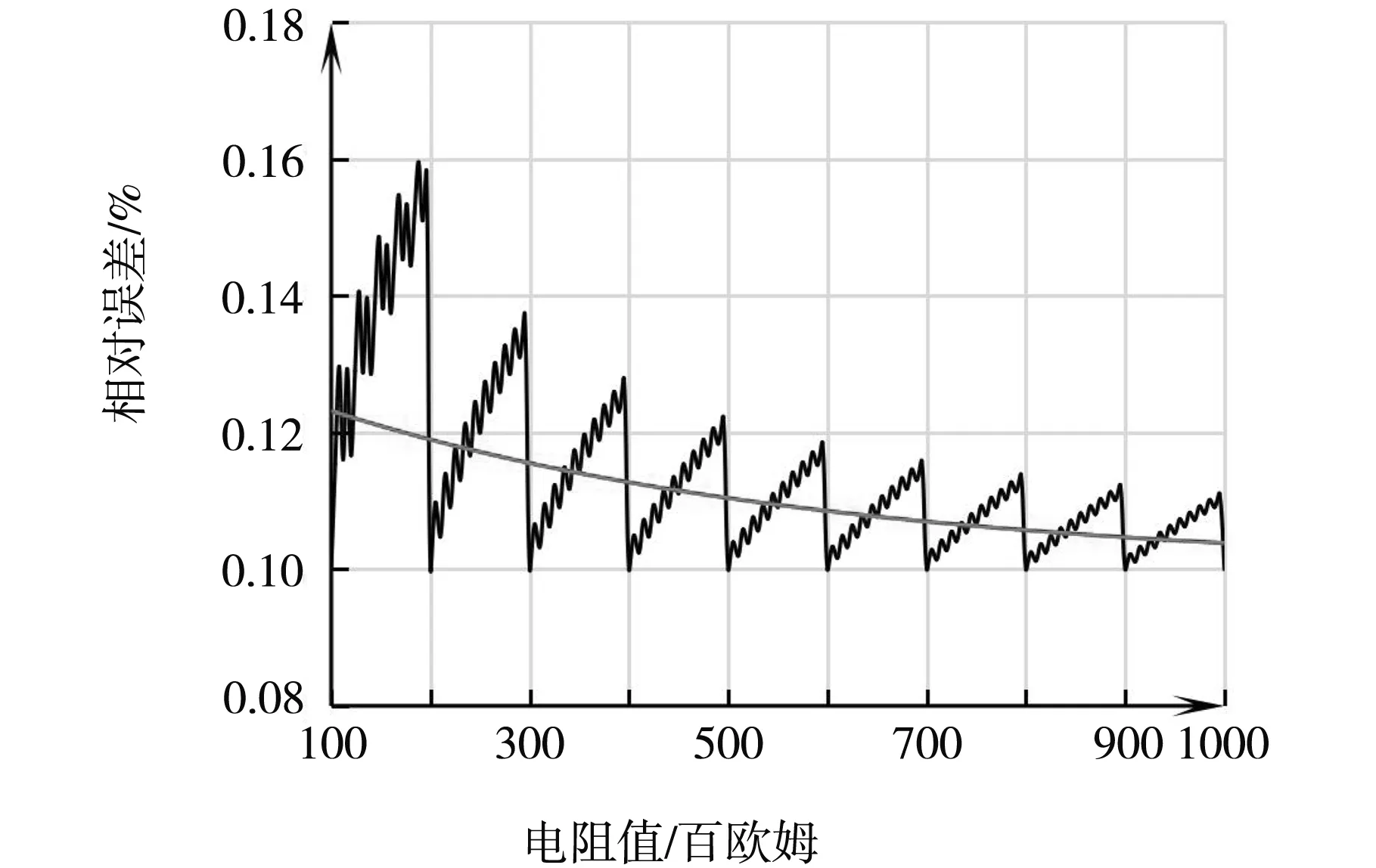
图2 电阻箱阻值的相对误差随阻值的变化曲线及其拟合曲线

因此，由各电阻箱的阻值误差所带来的待测电阻Rx的测量相对误差为

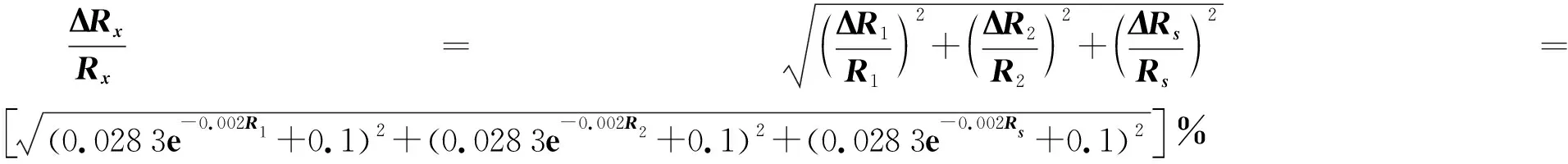
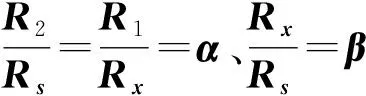
(7)

3 惠斯通电桥的测量误差

电阻Rx的测量误差是由电阻箱所产生的误差和电桥的灵敏度所产生的误差两者叠加而成。一般电桥的灵敏度被定义为：检流计指针偏转的格数与对应的比较臂电阻的相对变化之比[8]，即

(8)

从式(1)可得，当电桥平衡时有

成立，也即比较臂电阻的相对变化即为待测电阻的相对变化[9]，因此式(8)可以改写为

(9)

将一般肉眼在明视距离的分辨率Δn=0.2格代入式(9)，即得电桥的灵敏度所带来的相对误差：

(10)

于是，根据误差的叠加法则，惠斯通电桥的总测量相对误差可以表示为

(11)

将式(4)、(7)代入式(11)，则得以α、β为两变量的相对误差表达式：

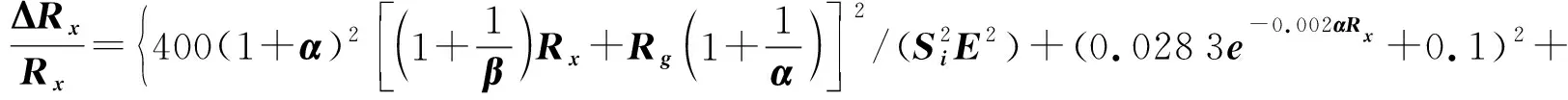
(12)

(13)

接下来，本文将分别以常见的待测电阻Rx=100Ω,1 000Ω,5 000Ω,10 000Ω为例，通过对式(13)求极(小)值，从而获得最佳的桥臂电阻比例关系α和β，以及相应的桥臂阻值。

1)当Rx=100Ω时

将Rx=100Ω代入式(13)得

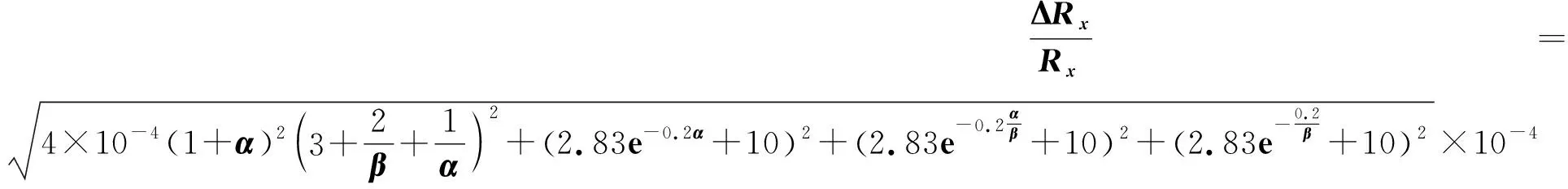
(14)

将式(14)分别对α和β求偏导，并令其结果皆为零，则得

(15)

(16)

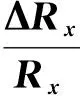
(17)

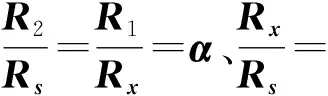
(18)

从理论上讲(见式(14))，此时Rx的测量相对误差最小，值为1.831×10-3。

数据表明，在上述理想的比例臂阻值附近，Rx的相对误差随各电阻值的变化是十分缓慢的。因此，在实际的操作中，R1和R2的取值可以分别在765Ω和6 251Ω左右浮动。考虑到实际电阻的台阶状误差(非拟合函数式(6)，见图2)，R1和R2应尽可能取邻近的整值电阻(百欧姆的整数倍，下同)，比如分别取800Ω和6 300Ω，这样处理，最终的实际相对误差，有可能会比取765Ω和6 251Ω时的理论相对误差极小值1.831×10-3还要小或者大致相当。本文求极值所得理论结果式(17)、(18)的价值，在于从总体趋势上确定大致最佳的桥臂比例或阻值，为实验操作提供理论上的指导，但是式(17)、(18)本身并不具备严格而绝对的意义。事实上，当R1、R2分别取800Ω、6 300Ω时，可算得Rs=787.5Ω,α=8,β≈0.127 0；再根据表1、式(11)中的电阻误差表达式、式(14)中的灵敏度误差表达式，即可算得此时电桥严格的相对误差值为1.848×10-3，它与上文理论上的最小值1.831×10-3大致相当，仅相差1.7×10-5的相对误差。

2)当Rx=1 000Ω时

将Rx=1 000Ω代入式(13)得

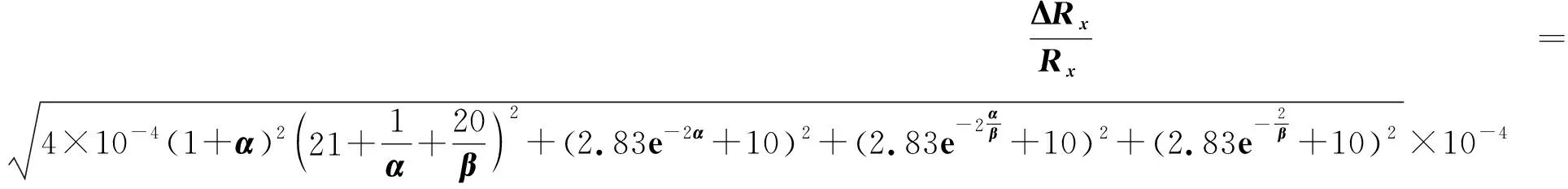
(19)

将式(19)分别对α和β求偏导，并令其结果皆为零，则得

(20)

(21)

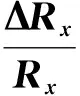
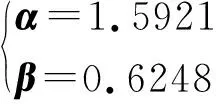
(22)

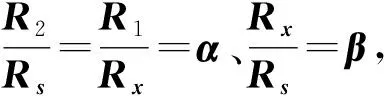
(23)

在本文的理论上(见式(19))，此时Rx的测量相对误差最小，值为1.768×10-3。

与上例同理，在实际的操作中，R1和R2可以分别取附近的1 600Ω和2 500Ω。经计算，此时电桥的实际相对误差为1.780×10-3，与理论上的极小值大致相当。

3)当Rx=5 000Ω时

将Rx=5 000Ω代入式(13)得

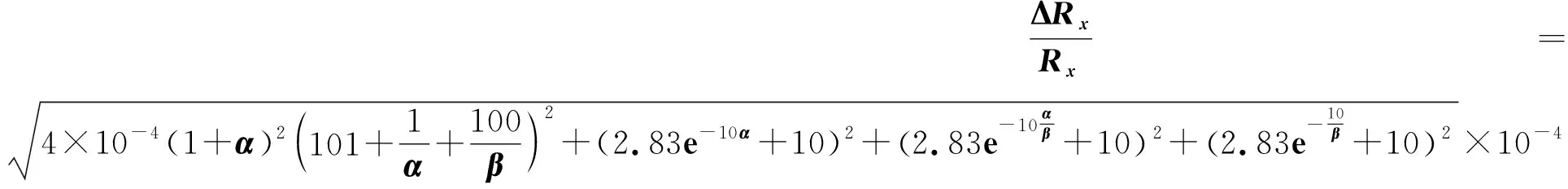
(24)

将式(24)分别对α和β求偏导，并令其结果皆为零，则得

(25)

(26)

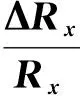
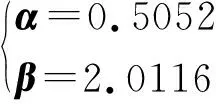
(27)

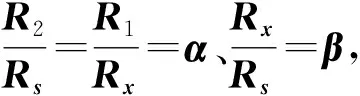
(28)

从理论上讲(见式(24))，此时Rx的测量相对误差最小，值为1.807×10-3。

与上文同理，在实际的操作中，R1和R2可以分别取附近的2 500Ω和1 300Ω。经计算，此时电桥的实际相对误差为1.793×10-3，比理论上的极小值还要小一点。

4)当Rx=10 000Ω时

将Rx=10 000Ω代入式(13)得

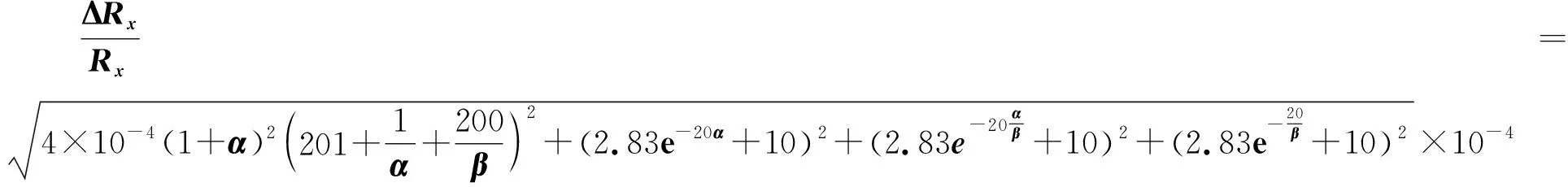
(29)

将式(29)分别对α和β求偏导，并令其结果皆为零得

(30)

(31)

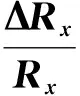
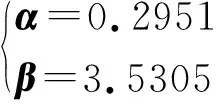
(32)

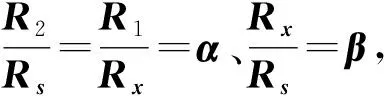
(33)

从理论上讲(见式(29))，此时Rx的测量相对误差最小，值为1.889×10-3。

与上文同理，在实际的操作中，R1和R2可以分别取附近的3 000Ω和800Ω。经计算，此时电桥的实际相对误差为1.875×10-3，同样也比理论上的极小值小一点。

4 补充说明

如果检流计的指针很细且测量观察十分小心，则检流计的人眼分辨率可以达到Δn=0.1格，那么上文第3节中由灵敏度所带来的测量误差将减小一半。在对相应的公式作出微调后，按照同样的方法，可以数值求得R1、R2在理论上的最佳电阻值，如表2所示。由于此时电桥的灵敏度误差权重减小了许多，因此电阻箱的误差权重势必增大不少。按照上文的理论分析，包括电阻箱的误差总体随阻值的增大而减小的结论可知，此时R1、R2的理论最佳阻值，相较第3节中的结果，理应增大不少，并且相应的总误差势必减小(灵敏度误差减小了)。当然，在实际操作时，R1、R2同样可以取最佳值附近的整值电阻。这里有一点需要说明一下：尽管数据表明最终的总误差一般主要来自电阻箱的阻值误差，但是这两种误差随R1、R2阻值变化的幅度却彼此不逞多让！因此，在通过求总误差的极小值求R1、R2的最佳阻值时，这两种误差的贡献均必须考虑。

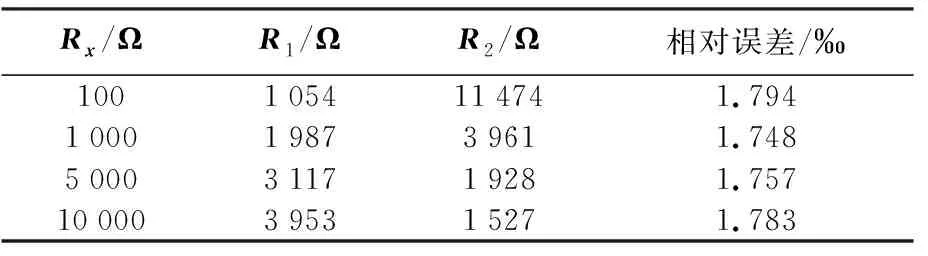
表2 检流计指针的分辨率为0.1格时R1、R2的理论最佳阻值及相应的测量误差

需要说明的是，目前市场上大多数ZX21型电阻箱的多档阻值的准确度相较于本文中的早期产品均有所下降，详见表3及表1，其阻值的相对误差随阻值的变化曲线经计算如图3所示，易见该变化曲线在1 000Ω位置有一个骤然的下降，这些与图2中早期产品的变化曲线有着较明显的区别，主要表现在1 000Ω以下阻值的相对误差明显偏大，达到了0.5%～0.8%。因此，在使用这种电阻箱搭建的惠斯通电桥测量电阻时，R1、R2均应选择在1 000Ω以上，同时设法使Rs也处在1 000Ω以上，这样才能有效地回避该电阻箱的小值电阻误差。然而，从严格测量的角度讲，还是应当首选误差较小的电阻箱来搭建惠斯通电桥测量未知电阻，因此本文仍然选择了早期精度较高的电阻箱来计算电桥的理论误差，进而计算出误差最(极)小时R1、R2理论上的最佳阻值。

表3 市面上多数ZX21型电阻箱各档阻值的实际准确度fj

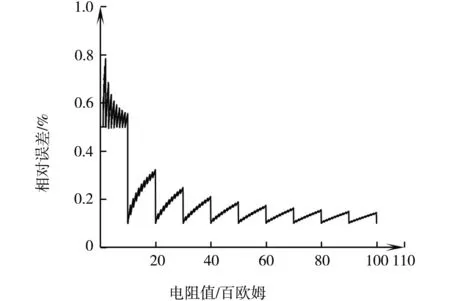
图3 市面上多数ZX21型电阻箱阻值的相对误差随阻值的变化曲线

5 结 语

通过对惠斯通电桥灵敏度的理论研究，发现惠斯通电桥的灵敏度并无极大值或者最大值之说。影响惠斯通电桥的精确度的主要因素有电桥的灵敏度和电阻箱自身的误差，通常(正常理性地测量)后者最终的影响会更大一些。鉴于电阻箱的误差曲线呈现不连续的锯齿状，为了简化问题从而获得定性或者半定量的有价值的结论，本文采用了指数函数对该误差曲线进行了拟合，从而获得电阻箱阻值近似的相对误差函数，进而运用对系统的总误差求极小值的方法从理论上计算出大致最佳的桥臂比例和阻值。

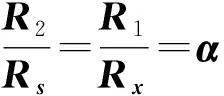
数据表明，在理想的比例臂阻值附近，Rx的相对误差随各电阻值的变化十分缓慢，因此在实际的操作中，R1和R2可以分别取各自理想值附近的整值电阻，如此实验误差可能会更小一些或者大致相当。另外，由于我们在做实验时，一般是将R1、R2固定，通过改变Rs来测Rx的值，因此Rs的最终数值是不确定的，在实际操作时，只需要考虑R1、R2取整值电阻即可，Rs是否取整则无需考虑。

虽然本文的理论结果不尽严格，但是本文的研究思路、方法和结论，或可为惠斯通电桥实验提供一些理论上的指导，亦可为其他相关的理论性研究提供一些线索及参考。本文的思路与方法同样可以用来计算由市面上的多数ZX21型电阻箱所组建的惠斯通电桥的最佳桥臂阻值R1和R2，本文在此从略。最后，需要特别说明的一点是，本文所计算的总系统误差或者说总系统不确定度式(11)，属于合成后的理论统计误差，经实验检验，它存在着明显的高估成分，实际的测量误差往往显著地小于该理论误差值，但是这并不妨碍本文的理论意义和价值。