一种基于卡尔曼滤波改善控制器的温度畸变控温系统设计

高 杨，王铁军，佟尧，刘旭峰，周易，武俊虎

(中国航发沈阳发动机研究所,辽宁 沈阳 110015)

航空发动机的气动稳定性是评估发动机性能的重要指标,要求发动机在整个飞行包线内均能够抵御降稳因素的干扰,保证足够的可用稳定裕度[1-3]。进气温度畸变是影响发动机稳定工作的外部因素之一,发动机抵抗温度畸变的能力直接决定了飞机的飞行性能以及任务能力。现役战斗机往往装配空空导弹和重型航炮等武器,导弹发射排出的尾流和航炮射击时产生的高温气体可能被进气道吸入,导致发动机入口产生严重的温度畸变,严重时将导致发动机空中停止。因此,随着战机实际应用需求的不断提升,温度畸变对航空发动机稳定工作的影响日益凸显,考虑到温度畸变问题的复杂成因和严重后果,设计搭建温度畸变模拟试验装置,摸清温度畸变发生机理显得尤为重要。

国外对于温度畸变发生器的设计较早,20 世纪70 年代末到80 年代初,美国和俄罗斯就先后建立了各自的温度畸变试验设备,并在大量试验研究的基础上颁布了发动机进口温度畸变评定指南[4]。Biesiadny T J 研究设计了小涡轴发动机压缩试验系统[5]。Rudey R A 进行了涡扇发动机空间和时间的进口温度畸变试验研究,利用氢气为燃料的燃烧室产生畸变[6]。国内研究进口温度畸变起步时间较晚,近年来取得很大进步。刘大响[7]等经过多年研究,积累了丰富的经验,对进气道发动机流场匹配提供了技术支持和评定指南。中国航发燃气涡轮研究院自主设计了温度畸变发生器,并调试成功,其测控系统主要基于早期工业控制技术,主要技术手段大都基于经典比例积分微分(Proportional Integral Differential,PID)控制。代冰[8]等对美俄航空发动机稳定性标准进行了对比分析,美国和俄罗斯都依据标准对其航空发动机稳定性作出评定,其总体思路是一致的,美国的畸变试验相对复杂,而俄罗斯的发动机畸变试验更强调工程应用。综上所述,国外试验设备开发设计较早,可见资料表明美俄畸变设备控制系统精度较高,大都采用通用工业技术设计实现。国内起步较晚,集成度一般,自动化程度不高。结合近几年国内工业设备技术发展状况,我们针对基于自研的温度畸变试验装置控制系统自动化不足的情况,进行了充分设计,以提高试验设备的工程应用水平。

以上工程实践中为了改善温度畸变装置的控制精度,获得理想的试验进气温度,大都设计闭环控制器以实现温度闭环控制,其控制方法大都应用经典的PID 控制器。这里我们设计在喷射试验前对喷口进行管线温度的预加热工作,使其稳定在某一温度。首先应用经典PID 闭环控制[9-11],虽然调试参数方向明确,易于理解,但在温度畸变装置的实际应用中,试验现场存在大量不确定性干扰因素,如测量噪声、干扰信号、管线热容波动等,这对于单一的经典PID 控制来说,控制效果显得十分有限,需要通过改进控制结构以改善控制输出。基于此,本文设计加入了卡尔曼滤波器[12-13],在PID 闭环控制的基础上进行控制效果的改善,系统基于PLC[14-15]硬件搭建,以SCL 编程方式实现控制运算。试验结果表明,本文方法克服了单一PID 控制器的局限性,提高了温度畸变装置的控温效果,且可靠性较高,最终现场试验结果验证了本文方法的优越性。

1 温度畸变装置的原理

温度畸变装置由送气管线、加温器、切换阀及调节阀组成,调试阶段由调试装置代替发动机,如图1所示。气源来气通过加温器的加热提高到一定的温度,打开切换阀门1、2,改变调节阀1、2 的低开度阀位,对主、辅进气喷口管线进行预热,预热结束后,关闭切换阀2,切换阀1 保持打开状态。此时将发动机工作模式改变为预试验状态,同时根据主、辅喷口流量配比改变调节阀1、2 的试验阀位状态,就绪后,迅速关闭切换阀1,打开切换阀2,将一定流量和温度的试验进气持续喷入发动机的主、辅进气道,观察记录发动机工作情况,至此完成一次温度畸变模拟试验。

2 系统软、硬件设计

发动机试验现场情况复杂,振动大,噪声干扰强,对控制系统提出了较高的可靠性要求,本文设计了基于可编程逻辑控制器(Programmable Logic Controlled,PLC)的测控系统,并通过SCL 编程实现了控制运算及算法解析。PLC 是一种数字运算操作的电子系统,专为在工业环境应用而设计。它采用一类可编程的存储器,用于其内部存储程序,执行逻辑运算、顺序控制、定时、计数与算术操作等面向用户的指令,并通过数字或模拟式输入/输出控制各种类型的机械或生产过程,是工业控制的核心部分。PLC 硬件原理结构如图2 所示。

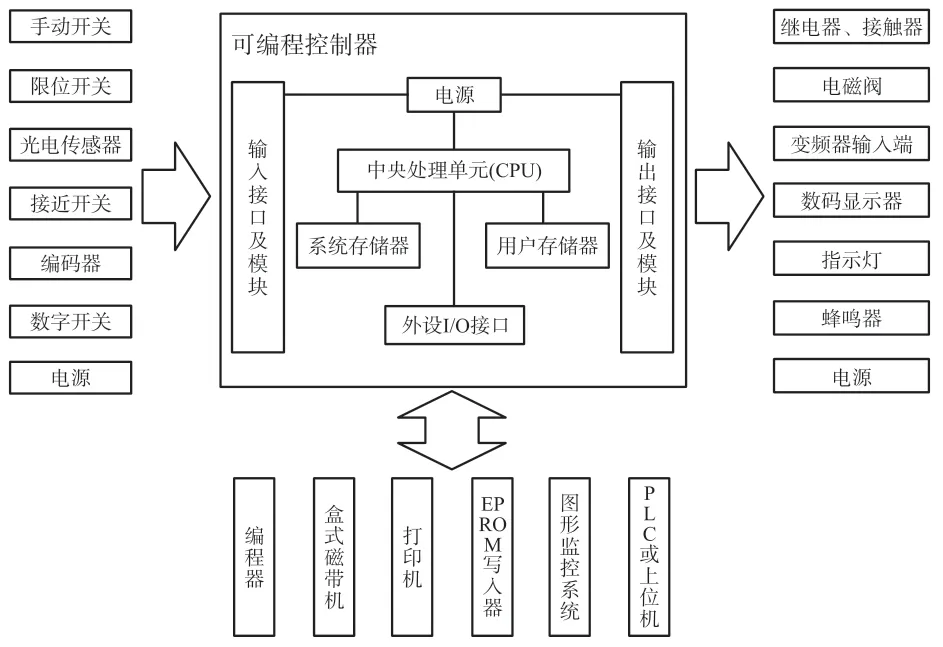
图2 PLC 硬件原理结构

本系统搭建的硬件拓扑结构组成如图3 所示。设计人机交互界面如图4 所示。

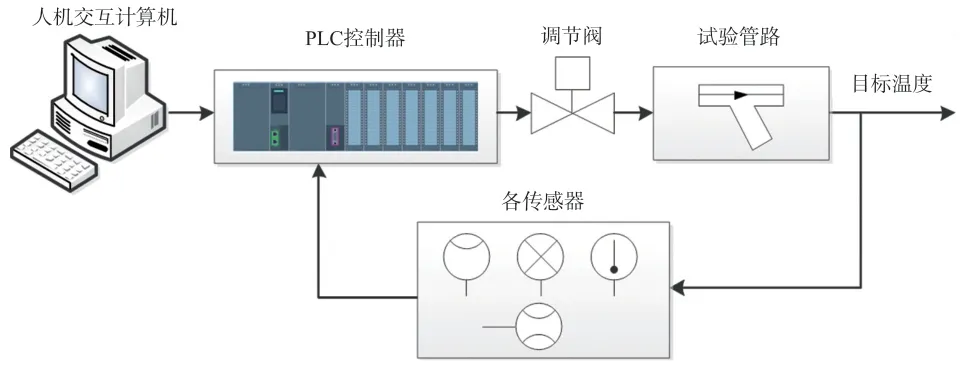
图3 硬件系统拓扑结构

图4 温度畸变试验测控系统界面

3 经典PID 控制器设计

针对预热温度控制,首先设计了经典PID 控制器,该控制器结构简单,参数调试方便,是工业现场中常用的控制技术。设计主、辅回路闭环PID 控制器结构如图5 所示。

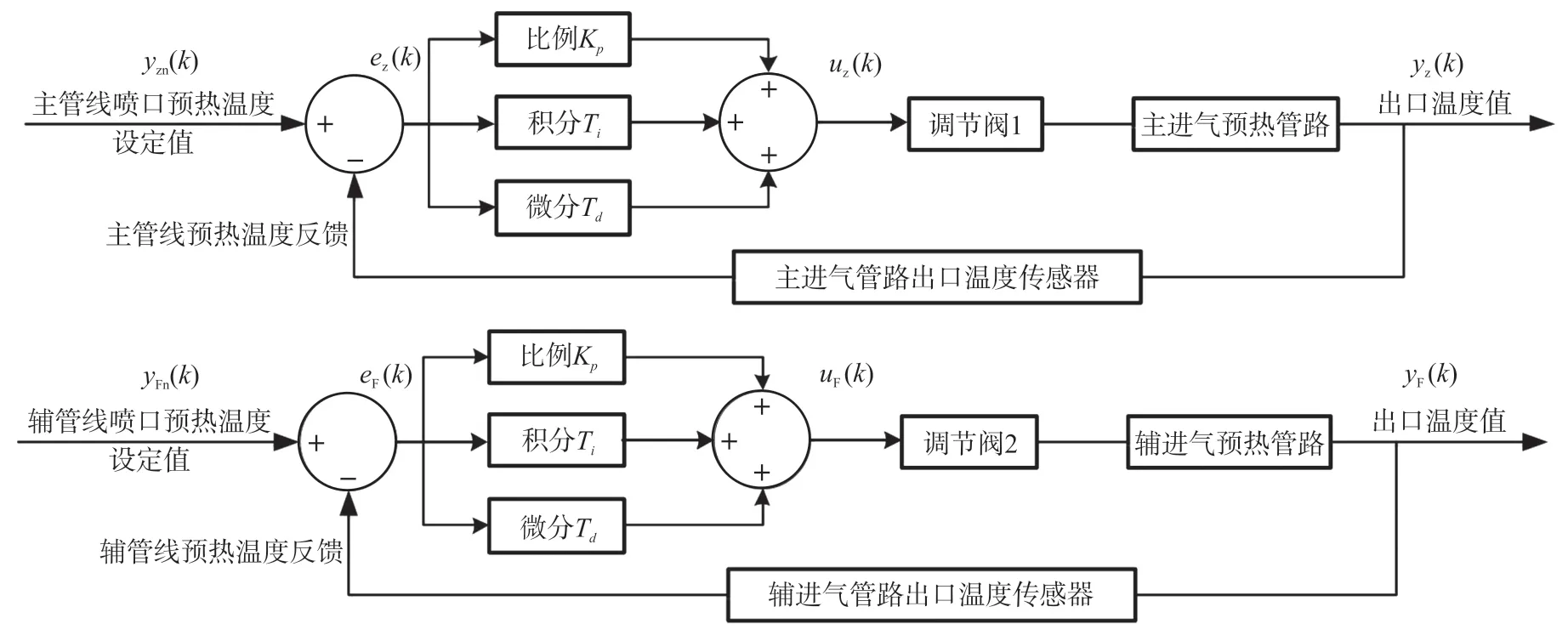
图5 预热PID 控制结构框图

主、辅喷口期望值yzn(k)与实际输出yz(k)之间的偏差为:

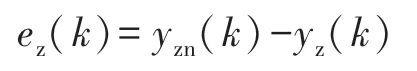
经典PID 控制规律为:

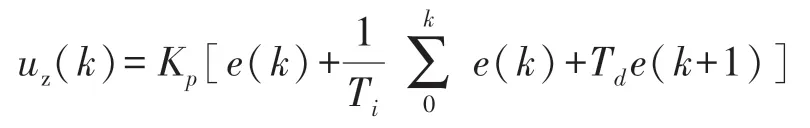
经过调试设计,主进气温度闭环控制回路比例参数Kp＝0.85,积分参数Ti＝40。辅进气温度闭环控制回路比例参数Kp＝0.95,积分参数Ti＝40,实际控制效果如图6 所示。从结果来看,所设计的PID 控制器基本实现预热温度的目标控制。图6(a)为主、辅喷口温度曲线,在150 s 内主、辅喷口温度可达到目标值稳态控制区间,调试时间及稳态误差满足试验设备的预热需求。但从图6(b)阀门动作曲线可以看出,在温度上升过程中明显可见存在波动干扰,主、辅阀门均波动明显,主阀位控制输出主要集中在0～10%,其控制过程相较稳态时波动范围为-10%～10%,辅阀位控制输出主要集中在8%～18%,其控制过程相较稳态时波动范围为-12%～12%。由于试验现场环境复杂,存在较大振动及干扰噪声信号,管道中来流的气体温度分布不均,都会对实际阀位的控制给定造成影响,实际使用中,主、辅调节阀高频次的执行动作会对阀门硬件设备造成损伤,PID 控制显然不满足实际使用需求,需要对其进行改进。

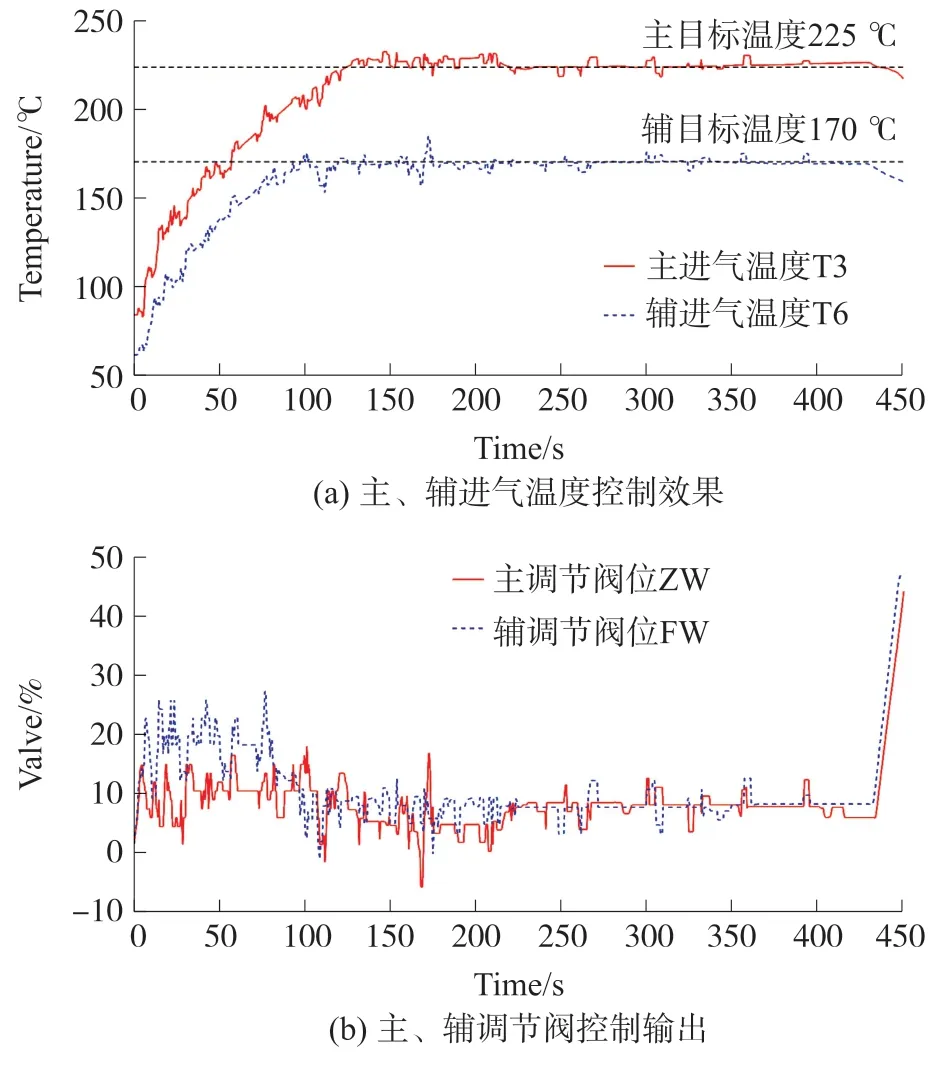
图6 预热PID 控制效果

4 卡尔曼滤波改善控制器设计

阀门的波动主要来自试验现场的复杂环境因素,干扰主要来自气体温度不均、试验管路高强度振动,即系统测量噪声及过程干扰噪声,干扰信号通过以上两种形式进入控制系统中,造成控制输出波动不稳。从图5 的控制系统回路中可以预见在控制回路中增加滤波控制器,可有效改善控制输出,减少波动。卡尔曼滤波作为当今主流的用于工控领域信息处理和有效滤波处理的基本算法,对于试验温度场景跟踪控制可以起到有效的修正作用。这里考虑控制系统中的测量过程及控制过程的实际情况,为解决阀门频繁动作及控制输出波动的问题,设计在控制回路中增加卡尔曼滤波器,即图8 所示的控制结构,以改善控制效果。

卡尔曼滤波理论基于维纳滤波理论发展而来,适用于频域、时域。设计改善控制,首先要得到实用可信的数学模型。

4.1 数学模型搭建

在温度畸变装置前期调试过程中积累大量数据,结合机械系统特性,搭建以调节阀阀位给定作为模型输入,喷口温度作为模型输出的单输入单输出数学模型,由于气体温度的变化特性,在模型结构中加入滞后环节。故模型结构如式:

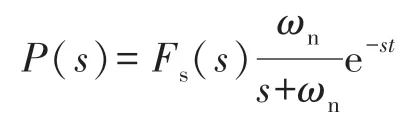
式中:Fs(s)为调节阀1(或调节阀2)阀位,Ps(s)为主进气喷口(或辅进气喷口)预热温度,ωn为该预热系统模型的固有频率,t为滞后时间,s为拉普拉斯算子。通过系统辨识得到主、辅喷口系统模型如下:

以上所得模型,在实际试验中与真实数据对比误差较小,模型置信度为90%,表明模型可用。

4.2 卡尔曼滤波改善控制器

4.2.1 卡尔曼滤波原理

卡尔曼滤波依据当前系统观测数据,计算状态最小二乘法意义下的最小均方差最优估计及最优权值,根据矩阵运算推导出卡尔曼滤波的“估计、预测、校正”,从而滤掉测量随机噪声及外界干扰,得到系统的准确空间状态值。

首先,得到系统线性离散化状态方程模型:

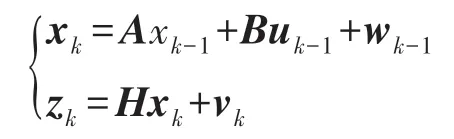
式中:xk是系统n维被估计状态变量；A是系统n×n维状态转移矩阵；B是系统n×l维控制输入u的增益矩阵；wk、vk分别为l维系统过程噪声和m维测量噪声矩阵；zk为系统m维测量变量；Hk为m×n维测量矩阵；R是系统过程噪声的非负方差矩阵；Q是系统观测噪声的对称正定方差；uk控制为本文设计PID控制。

卡尔曼滤波基本原理主要有5 个步骤:

基于上式,则t＝k时刻,随机线性离散卡尔曼滤波方程:

(1)状态变量的状态一步预测:

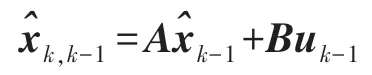
通过此方程可以由系统状态量xk的卡尔曼滤波的估计值,推导出系统的状态量xk的下一步预测值。其值通过t＜k-1 与t＝k-1 时刻系统观测值估计出来。

(2)状态估计:

式中:xk-为系统状态变量xk的一步预测误差,作用是系统进行卡尔曼估计的主要信息。

(3)滤波增益矩阵计算:

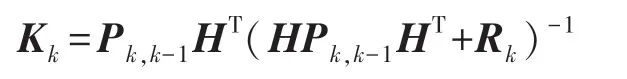
式中:Rk为系统观测噪声vk均方差矩阵；当Rk值变大时,Kk相应变小,噪声干扰较大时,新数据误差增大,滤波增益的值Kk应该小一些,来保证观测噪声干扰对滤波值有较小影响。

(4)一步预测误差协方差矩阵:

Pk,k-1为一步预测的均方误差矩阵,它是由系统噪声干扰方差与均方误差矩阵Pk-1推导出的。

(5)估计误差协方差矩阵:

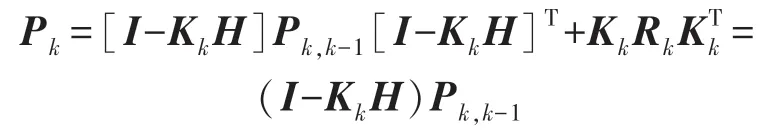
通过以上5 步反复迭代使得预测值的误差不断减小,最终改善系统控制效果。

4.2.2 改善控制器设计仿真

将上述线性连续喷口系统传递函数进行离散化处理,得到以下线性离散状态方程模型:

依据上述原理,如图7 所示,利用s函数建模仿真研究。根据未改进时系统介入噪声幅度,过程噪声取w(k)∈[-0.5,0.5],测量白噪声取v(k)∈[-0.5,0.5],噪声参数取Q＝10,R＝10。

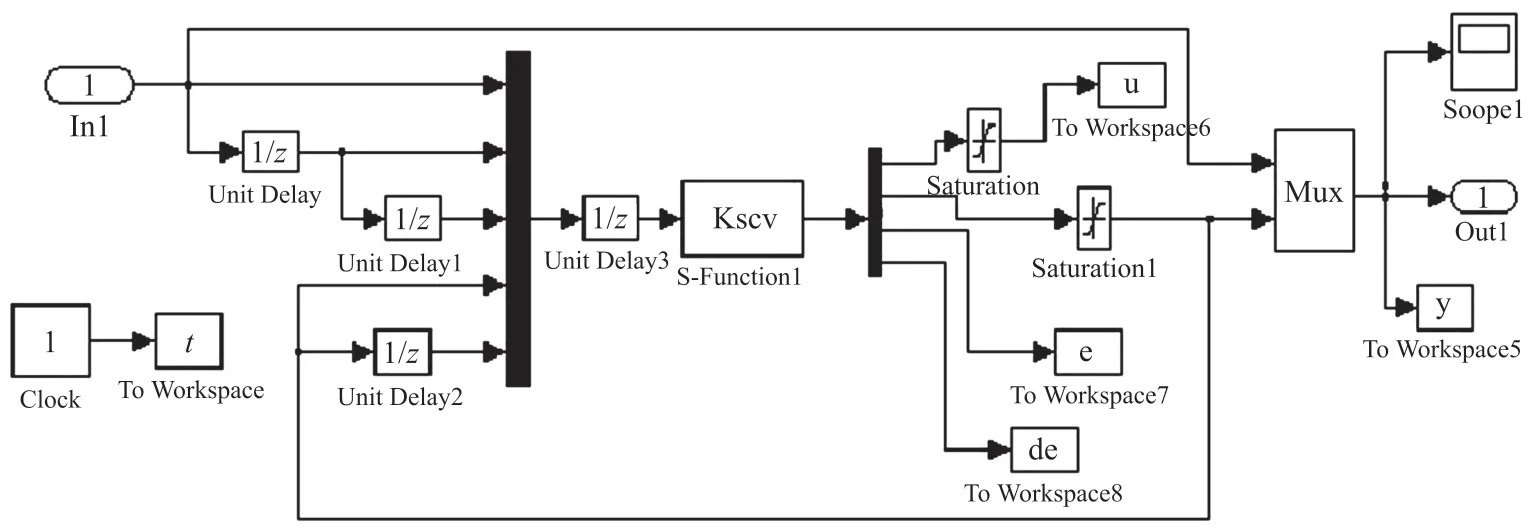
图7 卡尔曼滤波控制器模型

考虑实际控制系统,改进其控制结构如图8 所示,卡尔曼滤波改善控制器基于原有PID 控制结构,在控制回路中加入卡尔曼滤波器改善控制。其仿真结果如图9 所示,图9(b)中,左侧控制输出为阀门阀位信号,变化范围为0%～100%。故纵坐标为阀门阀位信号即真实的阀门开度。

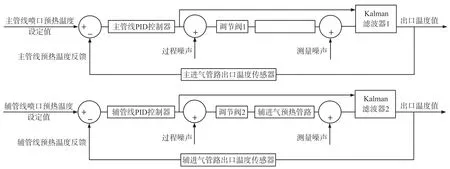
图8 卡尔曼滤波改善控制器

图9 卡尔曼滤波改善控制器仿真

从仿真结果来看,控温稳态误差明显减弱,同时阀门振动明显改善,达到预期,需进一步试验验证。

5 试验结果

利用SCL 编程的便利性,将所设计的卡尔曼滤波改善控制整合融入测控系统中,进行主进气目标温度225 ℃,辅进气目标温度170 ℃的预热试验,结果如图10 所示。从结果来看,加入卡尔曼滤波器后,波动明显减弱,控制效果持续改善,阀门波动减轻。具体对比结果如表1 所示。从表1 可知,卡尔曼滤波改善控制稳态误差相较PID 控制的相应误差大大减少,输出更加平缓。

表1 控制效果对比分析

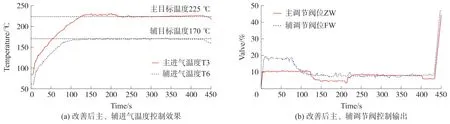
图10 改善后控制效果

改变控制目标为主235 ℃、辅160 ℃及主240 ℃、辅165 ℃等,控制效果如图11,图12 所示。从最终控制效果来看,控制输出阀位稳定,波动偏差在3%以内,稳态误差控制在3 ℃以内,表明此控制在一定控温目标范围内具有控制输出稳定,稳态误差小的特点,满足试验的实际使用需求,提高了控制精度和执行器(阀门)输出的波动性,大大提高了系统的稳定性。

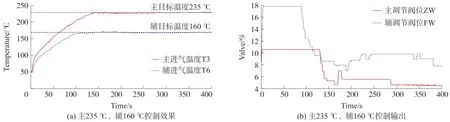
图11 主235 ℃、辅160 ℃控制效果

图12 主240 ℃、辅165 ℃控制效果

6 结论

本文基于卡尔曼滤波改善控制器所设计的温度畸变控温系统可将试验空气达到指定的温度状态,大大提高了温度畸变试验装置的自动化水平。最终试验结果表明,主阀位在0～15%之间,辅阀位在0～20%之间,主喷口温度可在220 ℃～250 ℃中任意温度点稳定,辅喷口温度可在150 ℃～170 ℃中任意温度点稳定,主、辅控温稳态误差可达到≯2%,大大缓解了控制阀门的高频波动,提升了试验的准确性。